Введение
Программистам числа Фибоначчи должны уже поднадоесть. Примеры их вычисления используются везде. Всё от того, что эти числа предоставляют простейший пример рекурсии. А ещё они являются хорошим примером динамического программирования. Но надо ли вычислять их так в реальном проекте? Не надо. Ни рекурсия, ни динамическое программирование не являются идеальными вариантами. И не замкнутая формула, использующая числа с плавающей запятой. Сейчас я расскажу, как правильно. Но сначала пройдёмся по всем известным вариантам решения.
Код предназначен для Python 3, хотя должен идти и на Python 2.
Для начала – напомню определение:
Fn= Fn-1+ Fn-2
и F1= F2=1.
Замкнутая формула
Пропустим детали, но желающие могут ознакомиться с выводом формулы. Идея в том, чтобы предположить, что есть некий x, для которого Fn = xn, а затем найти x.
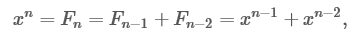
что означает
сокращаем xn-2
Решаем квадратное уравнение:
Откуда и растёт «золотое сечение» ϕ=(1+√5)/2. Подставив исходные значения и проделав ещё вычисления, мы получаем:
что и используем для вычисления Fn.
from __future__ import division
import math
def fib(n):
SQRT5 = math.sqrt(5)
PHI = (SQRT5 + 1) / 2
return int(PHI ** n / SQRT5 + 0.5)
Хорошее:
Быстро и просто для малых n
Плохое:
Требуются операции с плавающей запятой. Для больших n потребуется большая точность.
Злое:
Использование комплексных чисел для вычисления Fn красиво с математической точки зрения, но уродливо — с компьютерной.
Рекурсия
Самое очевидное решение, которое вы уже много раз видели – скорее всего, в качестве примера того, что такое рекурсия. Повторю его ещё раз, для полноты. В Python её можно записать в одну строку:
fib = lambda n: fib(n - 1) + fib(n - 2) if n > 2 else 1
Хорошее:
Очень простая реализация, повторяющая математическое определение
Плохое:
Экспоненциальное время выполнения. Для больших n очень медленно
Злое:
Переполнение стека
Запоминание
У решения с рекурсией есть большая проблема: пересекающиеся вычисления. Когда вызывается fib(n), то подсчитываются fib(n-1) и fib(n-2). Но когда считается fib(n-1), она снова независимо подсчитает fib(n-2) – то есть, fib(n-2) подсчитается дважды. Если продолжить рассуждения, будет видно, что fib(n-3) будет подсчитана трижды, и т.д. Слишком много пересечений.
Поэтому надо просто запоминать результаты, чтобы не подсчитывать их снова. Время и память у этого решения расходуются линейным образом. В решении я использую словарь, но можно было бы использовать и простой массив.
M = {0: 0, 1: 1}
def fib(n):
if n in M:
return M[n]
M[n] = fib(n - 1) + fib(n - 2)
return M[n]
(В Python это можно также сделать при помощи декоратора, functools.lru_cache.)
Хорошее:
Просто превратить рекурсию в решение с запоминанием. Превращает экспоненциальное время выполнение в линейное, для чего тратит больше памяти.
Плохое:
Тратит много памяти
Злое:
Возможно переполнение стека, как и у рекурсии
Динамическое программирование
После решения с запоминанием становится понятно, что нам нужны не все предыдущие результаты, а только два последних. Кроме этого, вместо того, чтобы начинать с fib(n) и идти назад, можно начать с fib(0) и идти вперёд. У следующего кода линейное время выполнение, а использование памяти – фиксированное. На практике скорость решения будет ещё выше, поскольку тут отсутствуют рекурсивные вызовы функций и связанная с этим работа. И код выглядит проще.
Это решение часто приводится в качестве примера динамического программирования.
def fib(n):
a = 0
b = 1
for __ in range(n):
a, b = b, a + b
return a
Хорошее:
Быстро работает для малых n, простой код
Плохое:
Всё ещё линейное время выполнения
Злое:
Да особо ничего.
Матричная алгебра
И, наконец, наименее освещаемое, но наиболее правильное решение, грамотно использующее как время, так и память. Его также можно расширить на любую гомогенную линейную последовательность. Идея в использовании матриц. Достаточно просто видеть, что
А обобщение этого говорит о том, что
Два значения для x, полученных нами ранее, из которых одно представляло собою золотое сечение, являются собственными значениями матрицы. Поэтому, ещё одним способом вывода замкнутой формулы является использование матричного уравнения и линейной алгебры.
Так чем же полезна такая формулировка? Тем, что возведение в степень можно произвести за логарифмическое время. Это делается через возведения в квадрат. Суть в том, что
где первое выражение используется для чётных A, второе для нечётных. Осталось только организовать перемножения матриц, и всё готово. Получается следующий код. Я организовал рекурсивную реализацию pow, поскольку её проще понять. Итеративную версию смотрите тут.
def pow(x, n, I, mult):
"""
Возвращает x в степени n. Предполагает, что I – это единичная матрица, которая
перемножается с mult, а n – положительное целое
"""
if n == 0:
return I
elif n == 1:
return x
else:
y = pow(x, n // 2, I, mult)
y = mult(y, y)
if n % 2:
y = mult(x, y)
return y
def identity_matrix(n):
"""Возвращает единичную матрицу n на n"""
r = list(range(n))
return [[1 if i == j else 0 for i in r] for j in r]
def matrix_multiply(A, B):
BT = list(zip(*B))
return [[sum(a * b
for a, b in zip(row_a, col_b))
for col_b in BT]
for row_a in A]
def fib(n):
F = pow([[1, 1], [1, 0]], n, identity_matrix(2), matrix_multiply)
return F[0][1]
Хорошее:
Фиксированный объём памяти, логарифмическое время
Плохое:
Код посложнее
Злое:
Приходится работать с матрицами, хотя они не так уж и плохи
Сравнение быстродействия
Сравнивать стоит только вариант динамического программирования и матрицы. Если сравнивать их по количеству знаков в числе n, то получится, что матричное решение линейно, а решение с динамическим программированием – экспоненциально. Практический пример – вычисление fib(10 ** 6), числа, у которого будет больше двухсот тысяч знаков.
n = 10 ** 6
Вычисляем fib_matrix: у fib(n) всего 208988 цифр, расчёт занял 0.24993 секунд.
Вычисляем fib_dynamic: у fib(n) всего 208988 цифр, расчёт занял 11.83377 секунд.
Теоретические замечания
Не напрямую касаясь приведённого выше кода, данное замечание всё-таки имеет определённый интерес. Рассмотрим следующий граф:
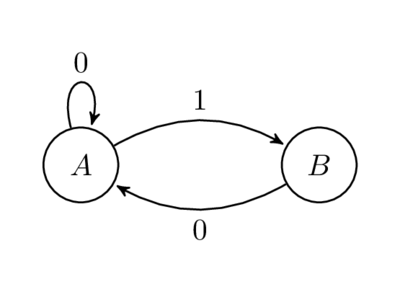
Подсчитаем количество путей длины n от A до B. Например, для n = 1 у нас есть один путь, 1. Для n = 2 у нас опять есть один путь, 01. Для n = 3 у нас есть два пути, 001 и 101. Довольно просто можно показать, что количество путей длины n от А до В равно в точности Fn. Записав матрицу смежности для графа, мы получим такую же матрицу, которая была описана выше. Это известный результат из теории графов, что при заданной матрице смежности А, вхождения в Аn — это количество путей длины n в графе (одна из задач, упоминавшихся в фильме «Умница Уилл Хантинг»).
Почему на рёбрах стоят такие обозначения? Оказывается, что при рассмотрении бесконечной последовательности символов на бесконечной в обе стороны последовательности путей на графе, вы получите нечто под названием "подсдвиги конечного типа", представляющее собой тип системы символической динамики. Конкретно этот подсдвиг конечного типа известен, как «сдвиг золотого сечения», и задаётся набором «запрещённых слов» {11}. Иными словами, мы получим бесконечные в обе стороны двоичные последовательности и никакие пары из них не будут смежными. Топологическая энтропия этой динамической системы равна золотому сечению ϕ. Интересно, как это число периодически появляется в разных областях математики.