Примечание: данный пост является переводом статьи cmcenroe.me/2014/12/05/days-in-month-formula.html (Часть I), а также авторским к нему дополнением (Часть II). Не следует относиться к материалу серьёзно, а скорее как к разминке для ума, требующей не более чем школьных знаний арифметики и не имеющей практического применения. Всем приятного чтения!
Недавно, после очередной бессонной ночи, я размышлял о методах запоминания количества дней в каждом месяце года. Для этого есть считалочка, а также способ считать на костяшках пальцев, но ни то, ни другое меня не устроило. Я задумался, а не существует ли какой-нибудь математической формулы для решения такой задачи, и — не обнаружив при беглом изучении таковую — бросил себе вызов её создать.
ФормализуяДругими словами, необходимо найти функцию f, такую, что значение f(x) для каждого месяца x, представленного числом от 1 до 12, равняется количеству дней в этом месяце. Таблица значений аргумента и функции1:
Если у вас возникло желание попробовать самому до прочтения моего решения, то сейчас самое время. Если же вы предпочитаете немедленно увидеть готовый ответ, то посмотрите под спойлер.
Ниже следуют мои шаги по нахождению решения.
Сначала бегло освежим в памяти два жизненно необходимых в решении этой задачи оператора: целочисленное деление и остаток от деления.
Целочисленное деление это оператор, применяемый во многих языках программирования при делении двух целых чисел и отбрасывающий от частного дробную часть. Я буду изображать его как . Например:
. Например:

Остаток от деления это оператор, находящий остаток от деления. Во многих языках программирования применяется символ %, я же буду использовать конструкции вида , например:
, например:

Замечу, что остаток от деления имеет равный с делением приоритет.
Итак, применим наш математический аппарат для получения базовой формулы.2 В обычном месяце 30 или 31 день, так что мы можем использовать для получения поочерёдно 1 или 0, а затем просто прибавить к этому числу константу:
для получения поочерёдно 1 или 0, а затем просто прибавить к этому числу константу:

Получаем таблицу, полужирным выделены корректные значения:
Неплохое начало! Уже есть правильные значения для января и для месяцев с марта по июль включительно. Февраль — особый случай, и с ним мы разберёмся чуть позже. После июля для оставшихся месяцев порядок получения 0 и 1 должен быть изменён на обратный.
Для этого мы может прибавить к делимому 1:
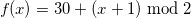
Теперь правильные значения с августа по декабрь, но, как и предполагалось, значения для прочих месяцев неверны. Давайте посмотрим как мы можем объединить эти формулы.
Для этого необходима кусочно-заданная функция, но — так как мне это показалось скучным — я задумался о другом пути решения, использующем одну часть функции на одном интервале, другую — на другом.
Полагаю, что проще всего будет найти выражение, равное 1 в одной области применения и 0 — в остальной. Метод, в котором умножая аргумент на выражение мы исключаем его из формулы вне области его применения, я назвал «наложением маски», потому такое поведение подобно некой битовой маске.
Для применения этого метода в последней части нашей функции необходимо найти выражение, равное 1 при , и — так как значения аргумента всегда меньше 16 — для этого прекрасно подходит целочисленное деление на 8.
, и — так как значения аргумента всегда меньше 16 — для этого прекрасно подходит целочисленное деление на 8.
Теперь с помощью этой маски, используя в делимом выражение
выражение  вместо 1, мы можем заменить порядок получения 0 и 1 формуле на обратный:
вместо 1, мы можем заменить порядок получения 0 и 1 формуле на обратный:
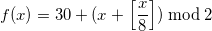
Эврика! Всё правильно, кроме февраля. Сюрприз-сюрприз.
В любом месяце 30 или 31 день, кроме февраля с его 28 (високосный год выходит за рамки этой задачи).3 На текущий момент по нашей формуле в нём 30 дней, поэтому неплохо бы вычесть выражение, равное 2 при .
.
Лучшее что мне удалось придумать это , что накладывает маску на все месяцы после февраля:
, что накладывает маску на все месяцы после февраля:
Изменив базовую константу на 28 с добавлением 2 к остальным месяцам получим формулу:

К сожалению, январь теперь короче на 2 дня. Но, к счастью, получить выражение, которое будет применяться только для первого месяца очень легко: это округлённое вниз обратное к число. Умножив его на 2 получаем окончательную формулу:
число. Умножив его на 2 получаем окончательную формулу:

Вот она — формула для получения количества дней в любом месяце года, использующая простейшую арифметику. В следующий раз когда вы будете вспоминать сколько же дней в сентябре, просто выполните с помощью этой однострочной функции на JavaScript:
с помощью этой однострочной функции на JavaScript:
В первой части была получена короткая и даже немного изящная формула, основными достоинствами которой являются простота математического аппарата, отсутствие ветвлений и условных выражений, лаконичность. К недостаткам — кроме того, что вы не будете применять её в вашем проекте — можно отнести отсутствие проверки на вискокосный и не високосный год.
Поэтому я поставил перед собой задачу создать функцию f, такую, что значение f(x, y) для каждого месяца x, представленного числом от 1 до 12 и года y, большего 0, равняется количеству дней в месяце x в году y.
Для нетерпеливых под спойлером находится готовый ответ, остальных же прошу следовать за мной.
Для визуальной наглядности договоримся, что в некоторых формулах оператор деления с остатком заменён нижними скобками, там где это показалось мне необходимым:
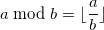
В високосный год вводится дополнительный день календаря: 29 февраля. Как известно, високосным является год, кратный 4 и не кратный 100, либо кратный 400. Запишем тождественное этому высказыванию выражение:
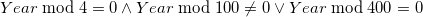
Для приведения этого выражения в алгебраическое, необходимо применить к результату выражения инъекцию вида:
инъекцию вида:
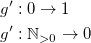
Что позволит получить 1 при делении без остатка и 0 при делении с остатком, чтобы использовать её в формуле определения количества дней в месяце.
В качестве функции g' можно использовать 1 минус остаток от деления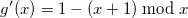 для
для  :
:
Легко заметить, что увеличив делимое и делитель на 1 мы получим правильную формулу при
при  :
:
Таким образом выражение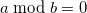 запишем как:
запишем как:
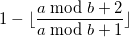
А выражение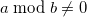 запишем как:
запишем как:

Применяя этот подход получим следующую функцию g(y), значением которой будет 1, если год високосный, или 0 в обратном случае:
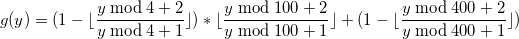
Полужирным выделены високосные года.
Напоминаю, что в рамках принятой договорённости оператор получения остатка от деления может быть изображен как mod, так и ⌊⌋.
В формуле часть
часть  является поправкой, прибавляющей 2 дня к январю. Если убрать множитель 2 и в числителе заменить 1 на 2, тогда эта формула будет прибавлять 2 дня к январю и 1 день к февралю, что даёт нам ключ к добавлению дня в високосном году. Для наглядности используем в формуле промежуточное значение g(y) и в качестве y используем 2000 (високосный) и 2001 (не високосный) годы:
является поправкой, прибавляющей 2 дня к январю. Если убрать множитель 2 и в числителе заменить 1 на 2, тогда эта формула будет прибавлять 2 дня к январю и 1 день к февралю, что даёт нам ключ к добавлению дня в високосном году. Для наглядности используем в формуле промежуточное значение g(y) и в качестве y используем 2000 (високосный) и 2001 (не високосный) годы:

Значения для всех месяцев, кроме января не високосного года верны.
Для исправления этого досадного недоразумения добавим к январю 1 день уже известной нам формулой :
:
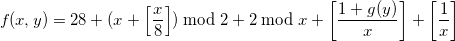
Теперь необходимо вычесть 1 день из января в случае високосного года, для чего нам поможет знание того, что для любого x , а
, а  .
.
Тогда формула примет вид:
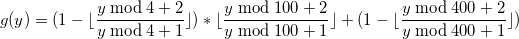
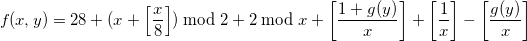
Или:

В результате получена уже значительно более громоздкая, но более универсальная формула, которую также можно использовать для получения количества дней в месяце определённого года:
Пример на C# ideone.com/fANutz.
1. Я не умею пользоваться подобной мнемоникой, поэтому подсмотрел табличку в интернете.
2. «Основы», или «Правило С Многими Исключениями», как и большинство правил.
3. Изначально в римском календаре февраль был последним месяцем года, поэтому есть логика в том, что он короче всех остальных. Также есть логика в добавлении или удалении дня именно в конце года, поэтому его длина является переменной.
Upd. 1:
Альтернативный перевод первой части в сообществе вконтакте.
Upd. 2: Благодаря комментарию keksmen исправлена ошибка в формуле определения високосного года (g(y)) и исправлена итоговая формула.
Часть I
Вступление
Недавно, после очередной бессонной ночи, я размышлял о методах запоминания количества дней в каждом месяце года. Для этого есть считалочка, а также способ считать на костяшках пальцев, но ни то, ни другое меня не устроило. Я задумался, а не существует ли какой-нибудь математической формулы для решения такой задачи, и — не обнаружив при беглом изучении таковую — бросил себе вызов её создать.
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f(x) | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
Если у вас возникло желание попробовать самому до прочтения моего решения, то сейчас самое время. Если же вы предпочитаете немедленно увидеть готовый ответ, то посмотрите под спойлер.
Ответ

Ниже следуют мои шаги по нахождению решения.
Математический аппарат
Сначала бегло освежим в памяти два жизненно необходимых в решении этой задачи оператора: целочисленное деление и остаток от деления.
Целочисленное деление это оператор, применяемый во многих языках программирования при делении двух целых чисел и отбрасывающий от частного дробную часть. Я буду изображать его как
 . Например:
. Например:
Остаток от деления это оператор, находящий остаток от деления. Во многих языках программирования применяется символ %, я же буду использовать конструкции вида
 , например:
, например:
Замечу, что остаток от деления имеет равный с делением приоритет.
Основы
Итак, применим наш математический аппарат для получения базовой формулы.2 В обычном месяце 30 или 31 день, так что мы можем использовать
 для получения поочерёдно 1 или 0, а затем просто прибавить к этому числу константу:
для получения поочерёдно 1 или 0, а затем просто прибавить к этому числу константу:
Получаем таблицу, полужирным выделены корректные значения:
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f(x) | 31 | 30 | 31 | 30 | 31 | 30 | 31 | 30 | 31 | 30 | 31 | 30 |
Неплохое начало! Уже есть правильные значения для января и для месяцев с марта по июль включительно. Февраль — особый случай, и с ним мы разберёмся чуть позже. После июля для оставшихся месяцев порядок получения 0 и 1 должен быть изменён на обратный.
Для этого мы может прибавить к делимому 1:
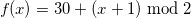
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f(x) | 30 | 31 | 30 | 31 | 30 | 31 | 30 | 31 | 30 | 31 | 30 | 31 |
Теперь правильные значения с августа по декабрь, но, как и предполагалось, значения для прочих месяцев неверны. Давайте посмотрим как мы можем объединить эти формулы.
Наложение маски
Для этого необходима кусочно-заданная функция, но — так как мне это показалось скучным — я задумался о другом пути решения, использующем одну часть функции на одном интервале, другую — на другом.
Полагаю, что проще всего будет найти выражение, равное 1 в одной области применения и 0 — в остальной. Метод, в котором умножая аргумент на выражение мы исключаем его из формулы вне области его применения, я назвал «наложением маски», потому такое поведение подобно некой битовой маске.
Для применения этого метода в последней части нашей функции необходимо найти выражение, равное 1 при
 , и — так как значения аргумента всегда меньше 16 — для этого прекрасно подходит целочисленное деление на 8.
, и — так как значения аргумента всегда меньше 16 — для этого прекрасно подходит целочисленное деление на 8.| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ⌊x⁄8⌋ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
Теперь с помощью этой маски, используя в делимом
 выражение
выражение  вместо 1, мы можем заменить порядок получения 0 и 1 формуле на обратный:
вместо 1, мы можем заменить порядок получения 0 и 1 формуле на обратный: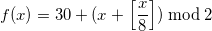
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f(x) | 31 | 30 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
Эврика! Всё правильно, кроме февраля. Сюрприз-сюрприз.
Февраль
В любом месяце 30 или 31 день, кроме февраля с его 28 (високосный год выходит за рамки этой задачи).3 На текущий момент по нашей формуле в нём 30 дней, поэтому неплохо бы вычесть выражение, равное 2 при
 .
.Лучшее что мне удалось придумать это
 , что накладывает маску на все месяцы после февраля:
, что накладывает маску на все месяцы после февраля:| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 mod x | 0 | 0 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
Изменив базовую константу на 28 с добавлением 2 к остальным месяцам получим формулу:

| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f(x) | 29 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
К сожалению, январь теперь короче на 2 дня. Но, к счастью, получить выражение, которое будет применяться только для первого месяца очень легко: это округлённое вниз обратное к
 число. Умножив его на 2 получаем окончательную формулу:
число. Умножив его на 2 получаем окончательную формулу:
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f(x) | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
Послесловие
Вот она — формула для получения количества дней в любом месяце года, использующая простейшую арифметику. В следующий раз когда вы будете вспоминать сколько же дней в сентябре, просто выполните
 с помощью этой однострочной функции на JavaScript:
с помощью этой однострочной функции на JavaScript:function f(x) { return 28 + (x + Math.floor(x/8)) % 2 + 2 % x + 2 * Math.floor(1/x); }Часть II
Вступление
В первой части была получена короткая и даже немного изящная формула, основными достоинствами которой являются простота математического аппарата, отсутствие ветвлений и условных выражений, лаконичность. К недостаткам — кроме того, что вы не будете применять её в вашем проекте — можно отнести отсутствие проверки на вискокосный и не високосный год.
Поэтому я поставил перед собой задачу создать функцию f, такую, что значение f(x, y) для каждого месяца x, представленного числом от 1 до 12 и года y, большего 0, равняется количеству дней в месяце x в году y.
Для нетерпеливых под спойлером находится готовый ответ, остальных же прошу следовать за мной.
Ответ

Остаток от деления: mod и ⌊⌋
Для визуальной наглядности договоримся, что в некоторых формулах оператор деления с остатком заменён нижними скобками, там где это показалось мне необходимым:
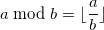
Високосный год
В високосный год вводится дополнительный день календаря: 29 февраля. Как известно, високосным является год, кратный 4 и не кратный 100, либо кратный 400. Запишем тождественное этому высказыванию выражение:
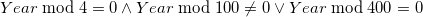
Для приведения этого выражения в алгебраическое, необходимо применить к результату выражения
 инъекцию вида:
инъекцию вида: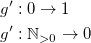
Что позволит получить 1 при делении без остатка и 0 при делении с остатком, чтобы использовать её в формуле определения количества дней в месяце.
В качестве функции g' можно использовать 1 минус остаток от деления
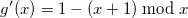 для
для  :
:| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| g'(x) | Infinity | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Легко заметить, что увеличив делимое и делитель на 1 мы получим правильную формулу
 при
при  :
:| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| g'(x) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Таким образом выражение
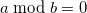 запишем как:
запишем как: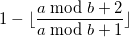
А выражение
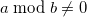 запишем как:
запишем как:
Применяя этот подход получим следующую функцию g(y), значением которой будет 1, если год високосный, или 0 в обратном случае:
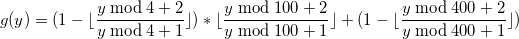
| y | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| g(y) | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| y | 2000 | 2100 | 2200 | 2300 | 2400 | 2500 | 2600 | 2700 | 2800 | 2900 | 3000 |
| g(y) | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
Полужирным выделены високосные года.
Напоминаю, что в рамках принятой договорённости оператор получения остатка от деления может быть изображен как mod, так и ⌊⌋.
Наложение маски
В формуле
 часть
часть  является поправкой, прибавляющей 2 дня к январю. Если убрать множитель 2 и в числителе заменить 1 на 2, тогда эта формула будет прибавлять 2 дня к январю и 1 день к февралю, что даёт нам ключ к добавлению дня в високосном году. Для наглядности используем в формуле промежуточное значение g(y) и в качестве y используем 2000 (високосный) и 2001 (не високосный) годы:
является поправкой, прибавляющей 2 дня к январю. Если убрать множитель 2 и в числителе заменить 1 на 2, тогда эта формула будет прибавлять 2 дня к январю и 1 день к февралю, что даёт нам ключ к добавлению дня в високосном году. Для наглядности используем в формуле промежуточное значение g(y) и в качестве y используем 2000 (високосный) и 2001 (не високосный) годы:
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f(x, 2000) | 31 | 29 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
| f(x, 2001) | 30 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 30 |
Значения для всех месяцев, кроме января не високосного года верны.
Для исправления этого досадного недоразумения добавим к январю 1 день уже известной нам формулой
 :
: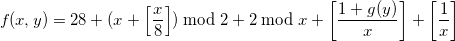
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f(x, 2000) | 32 | 29 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
| f(x, 2001) | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 30 |
Теперь необходимо вычесть 1 день из января в случае високосного года, для чего нам поможет знание того, что для любого x
 , а
, а  .
.Тогда формула примет вид:
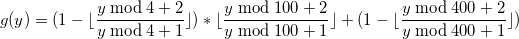
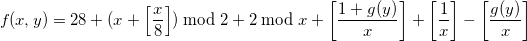
Или:

| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f(x, 2000) | 31 | 29 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
| f(x, 2001) | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 30 |
Заключение
В результате получена уже значительно более громоздкая, но более универсальная формула, которую также можно использовать для получения количества дней в месяце определённого года:
function f(x, y) { return 28 + ((x + Math.floor(x / 8)) % 2) + 2 % x + Math.floor((1 + (1 - (y % 4 + 2) % (y % 4 + 1)) * ((y % 100 + 2) % (y % 100 + 1)) + (1 - (y % 400 + 2) % (y % 400 + 1))) / x) + Math.floor(1/x) - Math.floor(((1 - (y % 4 + 2) % (y % 4 + 1)) * ((y % 100 + 2) % (y % 100 + 1)) + (1 - (y % 400 + 2) % (y % 400 + 1)))/x); }Пример на C# ideone.com/fANutz.
1. Я не умею пользоваться подобной мнемоникой, поэтому подсмотрел табличку в интернете.
2. «Основы», или «Правило С Многими Исключениями», как и большинство правил.
3. Изначально в римском календаре февраль был последним месяцем года, поэтому есть логика в том, что он короче всех остальных. Также есть логика в добавлении или удалении дня именно в конце года, поэтому его длина является переменной.
Upd. 1:
Альтернативный перевод первой части в сообществе вконтакте.
Upd. 2: Благодаря комментарию keksmen исправлена ошибка в формуле определения високосного года (g(y)) и исправлена итоговая формула.