Символьная регрессия считается очень интересной. "Найди мне функцию, которая будет лучше всего подходить для решения поставленной задачи". И на Хабре я уже встречал пост, в котором автор рассматривал один из эволюционных алгоритмов в применении к этой проблеме (вот он).
Генетическое программирование действительно является мощным методом. Но в этой статье я хочу рассмотреть другой (не менее интересный) метод — грамматическая эволюция. Рассказывать о нем долго не буду. Скажу лишь то, что метод использует свободную грамматику в форме Бакуса-Наура, а также любой эволюционный алгоритм в качестве "движка" (я выбрал генетический алгоритм). И метод очень крутой!
Перейду сразу к примеру. В качестве рабочей лошадки я выбрал Осциллятор Дуффинга.
Опишу задачу. Есть неоднородное дифференциальное уравнение второго порядка:
Делаем из него однородное (нефорсированный ОД):
После приведения уравнения к нормальной форме Коши получим следующую систему:
Пусть и вектор начальных условий
Вектор начальных условий будет равен [1,1]. Цель: получить такую функцию u(t,x), которая за минимальное время переведет систему из состояния [1,1] в [0,0].
Код системы дифур:
Duffing = [
lambda t,x: x[1],
lambda t,x: -x[0] - x[0]**3 + u(t,x)
]Осталось рассмотреть грамматику, которую я выбрал для метода:
grammar = {
'<expr>' : [
'(<expr>)<op>(<expr>)', '<val>', '<func1>(<expr>)'
],
'<op>' : [
'+', '-', '*', '/'
],
'<val>' : [
'x2', 'x1', '(smallConst)', '(bigConst)'
],
"<func1>": [
'minus','math.sin',
]
}Она примитивна, но дает нужный результат. Замечу, что smallConst — константа в интервале [0,1], а bigConst — константа в интервале [0,200].
Запускаем генетический алгоритм с параметрами
Длина хромосомы(каждое число в хромосоме — целочисленное значение в интервале от 0 до 200) = 10
Длина популяции = 50.
Число итераций (продолжительность эволюции) = 200.
Получаем следующий результат:
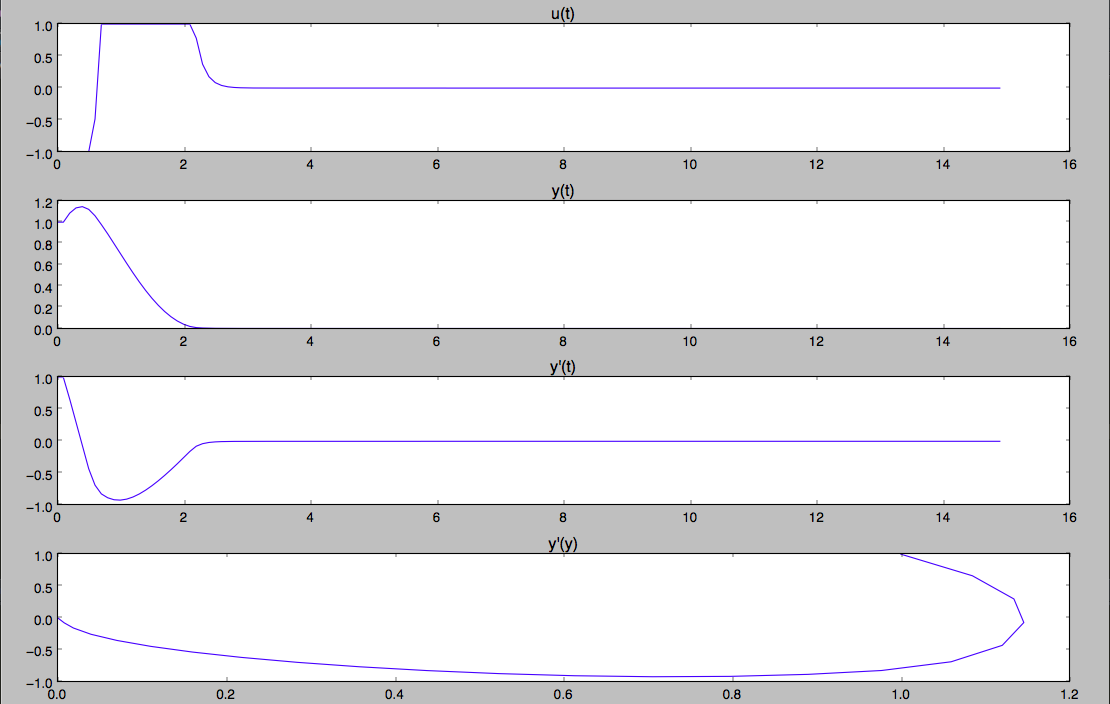
2.5 секунды — время переходного процесса.
u(t,x) = ((minus(x2))-((x1)((0.69028))))((11)) (довольно понятный вид, хотя много скобок)
Для получения среднего времени переходного процесса нужно запускать алгоритм не один раз(это очевидно). Но в этой статье я хотел показать, что алгоритм работает(!!) и дает результат.
Вывод: Грамматическая эволюция — молодой, но мощный инструмент в решении задач символьной регрессии. Да, не существует математически точного метода выбора той или иной грамматики для решаемой задачи. Нужно опираться на опыт и пробы с ошибками. Но метод работает и зачастую выдает приемлемый результат без оптимизированной грамматики.
Если кого-то заинтересовал ГЭ, то вот статья авторов этого метода (может быть, вскоре переведу).