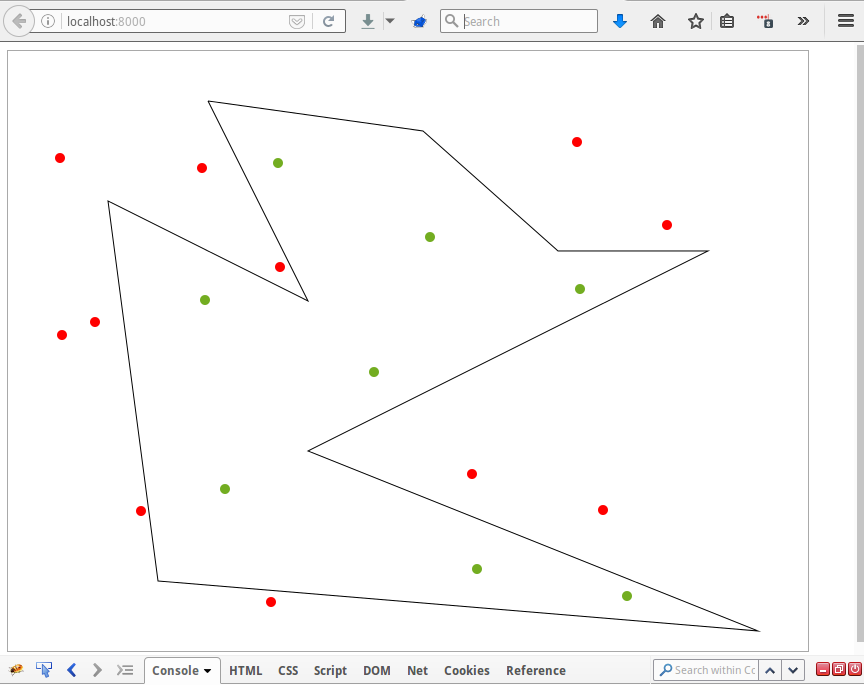
Вводная
Сразу оговорюсь кому может быть интересна данная публикация. Это начинающие Django + JQuery программисты, интересующиеся векторной графикой в браузере с использованием canvas. Или просто люди, получившие подобное задание.
Итак, находясь в постоянном сканировании рынка труда своего региона, наткнулся на весьма интересную вакансию web-разработчика в достаточно известной местной компании. В описании вакансии было сказано, что нужен python+django разработчик. После отправки резюме получил тестовое задание которое гласило:
Необходимо создать веб-приложение на Django, которое определяет факт вхождения точки в произвольный (не выпуклый) полигон. Клиентская часть должна отобразить в браузере (на канвасе или svg, или еще на чем-нибудь, в общем не принципиально) произвольный полигон, позволить пользователю указать точку на экране, отправить запрос на сервер, получить и отобразить ответ. Серверная часть, соответственно, должна принять запрос, определить, находится точка внутри контура, или нет, и вернуть ответ клиенту. Серверная часть на Python, клиентская — HTML + JavaScript либо CoffeeScript.
Потратив пару часов на выполнение задания и публикацию результата на тестовом сервере я уперся в полный игнор со стороны потенциального работодателя. Я не в обиде, бывает всякое, тем более задание было интересное и его выполнение принесло немало удовольствия. Чтобы добро не пропадало — публикую его здесь.
Поехали
Первым делом подготовим площадку, я использовал virtualenv:
scherbin@scherbin-pc ~$ cd WebDev/venvs
scherbin@scherbin-pc ~/WebDev/venvs/ $ virtualenv test
scherbin@scherbin-pc ~/WebDev/venvs/ $ cd test
scherbin@scherbin-pc ~/WebDev/venvs/test/ $ source bin/activate
Устанавливаем необходимый софт и прямо здесь создаем проект:
(test)scherbin@scherbin-pc ~/WebDev/venvs/test/ $ pip install django
(test)scherbin@scherbin-pc ~/WebDev/venvs/test/ $ django-admin startproject mytest
(test)scherbin@scherbin-pc ~/WebDev/venvs/test/ $ cd mytest
Наш проект будет состоять из двух приложений start и api. Первое будет отдавать браузеру пользователя HTML и JavaScript то есть наш frontend, второе будет обрабатывать AJAX запросы frontend-а, то есть будет нашим backend-ом. Создаем их:
(test)scherbin@scherbin-pc ~/WebDev/venvs/test/mytest/ $ django-admin startapp start
(test)scherbin@scherbin-pc ~/WebDev/venvs/test/mytest/ $ django-admin startapp api
Структура
Теперь, когда костяк проекта у нас есть, можно переходить непосредственно к творчеству. Для начала распишем структуру проекта. Как было указано выше, он будет состоять из двух частей, frontend и backend.
Frontend
Будет выводить в браузере, с использованием canvas, произвольный полигон и обрабатывать клики пользователя по нему. При клике backend-у посредством AJAX запроса будут передаваться две вещи в формате JSON:
- Массив координат полигона.
- Координаты точки куда кликнул пользователь.
После получения ответа на его основе в точке клика будет рисоваться круг диаметром 5 пикс. зеленого (входит в полигон) или красного (не входит) цвета.
Backend
Принимает запрос от frontend-а, вычисляет принадлежность точки полигону и возвращает результат в виде координат точки и boolean признака вхождения. Как видим многоугольник не хранится на сервере и есть потенциальная возможность использования и backend-а в случаях когда многоугольник меняется.
Реализация
Первым делом нам надо вывести наш полигон в браузере пользователя. Создаем главную (и единственную в нашем мини проекте) HTML страницу.
mytest/start/templates/start/index.html:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Тестовое задание</title>
{% load staticfiles %}
<script src="{% static 'js/jquery-1.12.0.min.js' %}"></script>
<script src="{% static 'js/main.js' %}"></script>
</head>
<body>
<style>
canvas#canvas-main {
border: 1px solid darkgray;
}
</style>
<canvas id="canvas-main"></canvas>
</body>
</html>
Как видно из кода на странице используется библиотека JQuery версии 1.12.0 и наш main.js файл где содержится JavaScript код, реализующий всю рутину. А именно рисование полигона, обработку кликов и связь с backend-ом. По сути это главный файл нашего мини проекта.
mytest/start/static/js/main.js:
$(function() {
/**
* Координаты нашего полигона
*/
var polygon = [
[200, 50],
[415, 80],
[550, 200],
[700, 200],
[300, 400],
[750, 580],
[150, 530],
[100, 150],
[300, 250],
[200, 50]
];
/**
* Размеры холста
*/
var canvasWidth = 800;
var canvasHeight = 600;
/**
* Функция вывода нашего полигона на холсте с использованием массива координат
*/
var drawPolygon = function(id, coords) {
var canvas = $("#"+id);
if (canvas.length) {
var context = canvas[0].getContext("2d");
context.canvas.width = canvasWidth;
context.canvas.height = canvasHeight;
context.beginPath();
for (var i = 0; i < coords.length; i++) {
if (i == 0) context.moveTo(coords[i][0], coords[i][1]);
else context.lineTo(coords[i][0], coords[i][1]);
}
context.strokeStyle = '#0000';
context.stroke();
}
};
/**
* Обрабатываем нажатия мышкой на холст
*/
$(document).on("click", "#canvas-main", function(event){
// ФИксируем координаты клика
var x = event.pageX-$(this).offset().left;
var y = event.pageY-$(this).offset().top;
// Готовим запрос к серверу. Запрос содержит координаты полигона и точки куда был произведен клик
var query = {
"polygon": polygon,
"point": [x, y]
};
// Получаем доступ к холсту
var context = $(this)[0].getContext("2d");
// Выполняем POST запрос к серверу
$.ajax({
type: "POST",
url: '/api/in_polygon',
data: JSON.stringify(query),
success: function(data) {
// ОБрабатываем полученный ответ
p = data['point'];
// Рисуем круг в точке клика
context.beginPath();
context.arc(p[0], p[1], 5, 0, 2 * Math.PI, false);
// По результату запроса заливаем круг зеленым или красным цветом
if (data['in_polygon'])
context.fillStyle = "#73AD21";
else
context.fillStyle = "#FF0000";
context.fill();
}
});
});
/**
* Рисуем полигон сразу после загрузки страницы
*/
drawPolygon("canvas-main", polygon);
});
Теперь необходимо реализовать саму проверку вхождения точки в полигон. Алгоритм использован самый простейший — трассировка луча. Последовательно проверяются все грани полигона на пересечение с лучом, идущим из точки, куда кликнул пользователь. Четное количество пересечений или нет пересечений вовсе — точка за пределами полигона. Количество пересечений нечетное — точка внутри. Далее python реализация в backend приложении api.
mytest/api/views.py:
# -*- coding: utf-8 -*-
import json
from django.http import HttpResponse, JsonResponse
# Create your views here.
def in_polygon(request):
if request.method == 'POST':
data = json.loads(request.body)
in_polygon = False
# Main algorithms
x = data['point'][0]
y = data['point'][1]
for i in range(len(data['polygon'])):
xp = data['polygon'][i][0]
yp = data['polygon'][i][1]
xp_prev = data['polygon'][i-1][0]
yp_prev = data['polygon'][i-1][1]
if (((yp <= y and y < yp_prev) or (yp_prev <= y and y < yp)) and (x > (xp_prev - xp) * (y - yp) / (yp_prev - yp) + xp)):
in_polygon = not in_polygon
response = {u'in_polygon': in_polygon, u'point': [x, y]}
return JsonResponse(response)
else:
return HttpResponse(u'Запрос должен использовать метод POST');
Теперь основной функционал готов. Осталось заставить все это дело работать. Для этого правим три файла.
mytest/mytest/settings.py
# Application definition
INSTALLED_APPS = [
...
'start',
'api',
]
mytest/mytest/urls.py
from django.conf.urls import *
from django.contrib import admin
from start.views import *
urlpatterns = [
url(r'^admin/', admin.site.urls),
url(r'^api/', include('api.urls')),
url(r'^$', start_index),
]
mytest/api/urls.py
from django.conf.urls import *
from api.views import *
urlpatterns = [
url(r'^in_polygon$', in_polygon, name='in_polygon')
]
С этого момента можно запускать встроенный в Django тестовый web сервер:
(test)scherbin@scherbin-pc ~/WebDev/venvs/test/mytest/ $ ./manage.py runserver
И играть в зеленые и красные точки перейдя в браузере по адресу localhost:8000/. Должна получиться картинка, аналогичная той, что в начале поста.