Математика — весьма интересная и занимательная наука, особое место в которой занимает вычисление числа Pi. История его вычисления занимает более 2х тысячелетий, а точность вычисления колеблется от 256/81 в древнем Египте и 339/108 в Ведах, до Джамшида ал-Каши, вычислившего 16 знаков в 15м веке. Чего стоит хотя бы история Вильяма Шенкса, который потратил 20 лет на вычисление 700 знаков числа Пи, но уже потом выяснилось, что во второй части расчетов он ошибся… Но текст в общем-то не об этом, а об алгоритмах. Стало интересно, можно ли вычислить Пи на iPhone? И если да, то с какой точностью?

Можно сказать сразу — миллион не предел. Можно и больше. Подробности и реализация под катом.
Даже животному семейства Erinaceidae (т.е. ежу) ясно что если мы хотим вычислить число Пи до миллиона знаков — типа float нам не хватит. И даже double тоже (где был тег «сарказм»?). Значит надо искать библиотеку для работы с длинными числами. На iOS используется Objective C (и Swift тоже но в данном случае он нам не нужен), который обратно совместим с Си, что несколько облегчает задачу — разных библиотек на Си довольно много. Небольшой поиск привел к библиотеке GMP, которая с одной стороны, делает то что нам нужно, с другой стороны, весьма проста в использовании.
Например, чтобы вывести 1000 знаков sqrt(3), достаточно следующего кода:
Полный список функций для работы с float можно найти здесь.
С библиотекой разобрались. Следующим встает вопрос, какой алгоритм использовать. Вопрос не совсем праздный, т.к. способов вычисления Пи довольно-таки много. Формула Белларда:

Формула Бэйли — Боруэйна — Плаффа:
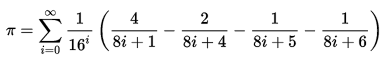
Формула Мачина:

Формула Чудновского (не спрашивайте меня как он ее вывел — не знаю):

Последняя формула на вид самая «страшная», но в то же время, самая быстрая.
Для проверки алгоритмов, все они были собраны в один файл на Питоне (он тоже поддерживает «длинные числа» в типе Decimal).
Результаты запуска скрипта:
Как можно видеть, даже с использованием факториала «в лоб» (что довольно долго), формула Чудновского быстрее предыдущих в 5-10 раз. Преобразование ее к виду без факториала (с использованием предыдущего значения) дает ускорение еще в несколько раз. В общем, победитель очевиден, но есть одно «но» — объем оперативной памяти. Если «идти на рекорд», и например считать миллиард знаков числа Пи, то критичным становится вопрос хранения данных в RAM. У iPhone всего лишь 1Гб памяти, причем для пользовательской программы доступно 512Мб. Если запросить примерно 600Мб, iOS просто закроет приложение. При подсчете миллиона знаков это еще не так критично (программа занимает в памяти не более 30Мб), но если брать больше, это станет критичным. И тут формула Чудновского будет в заметном проигрыше из-за сложности выполняемых операций, тут вполне могут пригодиться более простые алгоритмы.
Кстати о миллиарде знаков. Как показал запуск в симуляторе, при попытке создать число с миллиардом знаков, программа пытается выделить более 5Гб памяти, и при этом разумеется падает. По прикидкам, максимальное число, которое в принципе можно посчитать на iPhone, составляет около 200млн. знаков. На Android можно получить больше (кто бы сомневался:). Разумеется на вычисление уйдет не один день, но это уже другой вопрос.
Ниже приведен исходный код на Objective-C. Т.к. работа с библиотекой GMP несколько громоздка, код получился не очень красивым, но разобраться в принципе можно (да и на любом языке можно писать как на Фортране:).
Для тех кто захочет поэкспериментировать самостоятельно, здесь выложен исходный код проекта для XCode. Конечно, приведенный выше алгоритм не идеален, его например вполне можно распараллелить хотя бы на 2 потока. Или даже попробовать использовать Accelerate Framework.
При запуске на iPhone вылезли несколько забавных проблем. Первая — программа ни за что не хотела работать в бэкграунде, процесс вычислений просто останавливался. На тестовом iPhone 5S стояла iOS8, не знаю изменился ли принцип многозадачности в iOS9, но для 8ки решение оказалось простым — запустить GPS и подписаться на события от location service. При этом iOS «считает» что нам нужно постоянно получать координаты юзера, и позволяет программе работать даже в свернутом состоянии.
Вторая проблема вылезла минутой позже после первой. Как оказалось, iOS достаточно «умна», и считает подозрительным процесс, жрущий в фоне 100% ресурсов процессора. Видимо iOS считает что программа «повисла», и «убивает» ее примерно через минуту такой работы. Пришлось внутрь цикла вставить sleep с таким расчетом, чтобы «скважность» загрузки CPU была где-то 50/50. После этого программа могла считать и в фоновом режиме, хотя конечно скорость стала вдвое ниже. В итоге iPhone был просто подключен к зарядному устройству и оставлен на ночь, программа не закрывалась.
И наконец, обещанный результат: на iPhone 5S миллион знаков числа Пи вычислялись 49296 секунд, или около 14 часов. Кстати, на симуляторе с Core i7 время расчета составляет 4200 секунд, т.е. примерно в 11 раз быстрее. Интересно прикинуть, сколько будет вычисляться 100млн знаков. Оставляю это в качестве домашнего задания тем, кто дочитал до сюда. Также было бы интересно увидеть результаты для более новых (чем 5S) моделей iPhone. Программа во время расчетов показывает примерное время выполнения, результат сохраняется в папку iTunes file sharing.
Правка
В комментах подсказали сравнить программу с реализациями в Google Play. Как оказалось, там используется алгоритм Arithmetic-Geometric Mean (AGM), который действительно в разы быстрее. С последней версией вычисление миллиона знаков на iPhone 5S заняло 68 секунд.
Описание алгоритма и реализация на Python есть здесь: http://www.johndcook.com/blog/2012/06/03/calculating-pi-with-agm-and-mpmath/. C/С++ код для GMP доступен здесь: https://rosettacode.org/wiki/Arithmetic-geometric_mean/Calculate_Pi.
Тем кто захочет проверитьсвою память результат. Здесь на сайте лежит текстовый файл, содержащий миллиард знаков числа Пи, который собственно и использовался для проверки правильности результатов программы.
Что касается мирового рекорда (который для десктопа составляет 5трлн знаков, правда и десктоп был не рядовым), то вряд ли его удастся побить на смартфоне. Да и подобной таблицы рекордов для смартфонов вроде еще никто не делал. Однако дело конечно не в рекорде — как можно видеть, подобные расчеты представляют собой достаточно интересную инженерную задачу, где остаются открытыми вопросы оптимизации и памяти, и скорости вычислений, и многопоточности. В общем, есть где «пошевелить мозгами», что как раз и наиболее интересно в программировании.

Можно сказать сразу — миллион не предел. Можно и больше. Подробности и реализация под катом.
Реализация вычислений
Даже животному семейства Erinaceidae (т.е. ежу) ясно что если мы хотим вычислить число Пи до миллиона знаков — типа float нам не хватит. И даже double тоже (где был тег «сарказм»?). Значит надо искать библиотеку для работы с длинными числами. На iOS используется Objective C (и Swift тоже но в данном случае он нам не нужен), который обратно совместим с Си, что несколько облегчает задачу — разных библиотек на Си довольно много. Небольшой поиск привел к библиотеке GMP, которая с одной стороны, делает то что нам нужно, с другой стороны, весьма проста в использовании.
Например, чтобы вывести 1000 знаков sqrt(3), достаточно следующего кода:
#include "gmp.h"
#include "gmpxx.h"
mpf_set_default_prec(4096);
mpf_class num;
mpf_sqrt_ui(num.get_mpf_t(), 3);
gmp_printf("%.*Ff\n", 1000, num.get_mpf_t());Полный список функций для работы с float можно найти здесь.
Алгоритм
С библиотекой разобрались. Следующим встает вопрос, какой алгоритм использовать. Вопрос не совсем праздный, т.к. способов вычисления Пи довольно-таки много. Формула Белларда:

Формула Бэйли — Боруэйна — Плаффа:
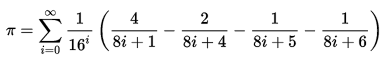
Формула Мачина:

Формула Чудновского (не спрашивайте меня как он ее вывел — не знаю):

Последняя формула на вид самая «страшная», но в то же время, самая быстрая.
Код
Для проверки алгоритмов, все они были собраны в один файл на Питоне (он тоже поддерживает «длинные числа» в типе Decimal).
Исходник под спойлером
import sys
import math
from decimal import *
from math import factorial
from time import time
# http://thelivingpearl.com/2013/05/28/computing-pi-with-python/
# http://www.numberworld.org/misc_runs/pi-5t/details.html
# Bellard's Formula PI
def bellard(n):
pi = Decimal(0)
k = 0
while k < n:
pi += (Decimal(-1)**k/(1024**k))*( Decimal(256)/(10*k+1) + Decimal(1)/(10*k+9) - Decimal(64)/(10*k+3) - Decimal(32)/(4*k+1) - Decimal(4)/(10*k+5) - Decimal(4)/(10*k+7) - Decimal(1)/(4*k+3))
k += 1
pi = pi * 1/(2**6)
return pi
# Bailey-Borwein-Plouffe formula
def bbp(n):
pi = Decimal(0)
k = 0
while k < n:
pi += (Decimal(1)/(16**k))*((Decimal(4)/(8*k+1))-(Decimal(2)/(8*k+4))-(Decimal(1)/(8*k+5))-(Decimal(1)/(8*k+6)))
k += 1
return pi
# http://www.craig-wood.com/nick/articles/pi-chudnovsky/
def chudnovsky(n):
pi = Decimal(0)
k = 0
while k < n:
pi += (Decimal(-1)**k)*(Decimal(factorial(6*k))/((factorial(k)**3)*(factorial(3*k)))* (13591409+545140134*k)/(640320**(3*k)))
k += 1
pi = pi * Decimal(10005).sqrt()/4270934400
pi = pi**(-1)
return pi
def chudnovsky2(n):
pi = Decimal(13591409)
ak = Decimal(1)
k = 1
while k < n:
ak *= -Decimal((6*k-5)*(2*k-1)*(6*k-1))/Decimal(k*k*k*26680*640320*640320)
val = ak*(13591409 + 545140134*k)
d = Decimal((6*k-5)*(2*k-1)*(6*k-1))/Decimal(k*k*k*26680*640320*640320)
pi += val
k += 1
pi = pi * Decimal(10005).sqrt()/4270934400
pi = pi**(-1)
return pi
# arctan
# http://www.craig-wood.com/nick/articles/pi-machin/
def arctan(x):
"""
Calculate arctan(1/x)
arctan(1/x) = 1/x - 1/3*x**3 + 1/5*x**5 - ... (x >= 1)
This calculates it in fixed point, using the value for one passed in
"""
x2 = x*x
x = Decimal(x)
total = Decimal(0)
sign = 1
for i in range(1, 512, 2):
#total += sign / (i * x)
total += sign / (i * x ** i)
sign = -sign
#x *= x2
#print(total)
return total
def pi_machin(n):
return 4*(4*arctan(5) - arctan(239))
def pi_gauss(one):
return 4*(12*arctan(18) + 8*arctan(57) - 5*arctan(239))
if __name__ == "__main__":
N = 1000
getcontext().prec = N
print ""
print "Atan"
start = time()
my_pi = pi_machin(N)
print "Pi = {}".format(str(my_pi))
print("Time", time()-start)
print "BBP"
start = time()
my_pi = bbp(N)
print "Pi = {}".format(str(my_pi))
print("Time", time()-start)
print "Bellard"
start = time()
my_pi = bellard(N)
print "Pi = {}".format(str(my_pi))
print("Time", time()-start)
print ""
print "Chudnovsky"
start = time()
my_pi = chudnovsky(N/14)
print "Pi = {}".format(str(my_pi))
print("Time", time()-start)
print ""
print "Chudnovsky2"
start = time()
my_pi = chudnovsky2(N/14)
print "Pi = {}".format(str(my_pi))
print("Time", time()-start)
Результаты запуска скрипта:
Формула Мачина: 2.01c
Формула Бэйли — Боруэйна — Плаффа: 1.42c
Формула Белларда: 1.82c
Формула Чудновского: 0.22c
Формула Чудновского (без факториала): 0.082c
Как можно видеть, даже с использованием факториала «в лоб» (что довольно долго), формула Чудновского быстрее предыдущих в 5-10 раз. Преобразование ее к виду без факториала (с использованием предыдущего значения) дает ускорение еще в несколько раз. В общем, победитель очевиден, но есть одно «но» — объем оперативной памяти. Если «идти на рекорд», и например считать миллиард знаков числа Пи, то критичным становится вопрос хранения данных в RAM. У iPhone всего лишь 1Гб памяти, причем для пользовательской программы доступно 512Мб. Если запросить примерно 600Мб, iOS просто закроет приложение. При подсчете миллиона знаков это еще не так критично (программа занимает в памяти не более 30Мб), но если брать больше, это станет критичным. И тут формула Чудновского будет в заметном проигрыше из-за сложности выполняемых операций, тут вполне могут пригодиться более простые алгоритмы.
Кстати о миллиарде знаков. Как показал запуск в симуляторе, при попытке создать число с миллиардом знаков, программа пытается выделить более 5Гб памяти, и при этом разумеется падает. По прикидкам, максимальное число, которое в принципе можно посчитать на iPhone, составляет около 200млн. знаков. На Android можно получить больше (кто бы сомневался:). Разумеется на вычисление уйдет не один день, но это уже другой вопрос.
Ниже приведен исходный код на Objective-C. Т.к. работа с библиотекой GMP несколько громоздка, код получился не очень красивым, но разобраться в принципе можно (да и на любом языке можно писать как на Фортране:).
Код под спойлером
#include "gmp.h"
#include "gmpxx.h"
- (void) calcPi {
/*
# Python source
pi = Decimal(13591409)
ak = Decimal(1)
k = 1
while k < n:
ak *= -Decimal((6*k-5)*(2*k-1)*(6*k-1))/Decimal(k*k*k*26680*640320*640320)
val = ak*(13591409 + 545140134*k)
pi += val
k += 1
#print "Iteration: {} of {}".format(k, n)
pi = pi * Decimal(10005).sqrt()/4270934400
pi = pi**(-1)
return pi
*/
unsigned long int bits = [self getBitsSize];
mpf_set_default_prec(bits);
NSDate *date1 = [NSDate date];
mpf_class pi = 13591409;
mpf_class ak = 1;
mpf_class v1, v2, v3, tmp1, d = 0, d1 = 0;
unsigned long int N = (unsigned long int)self.numDigits/14;
for(unsigned long int k=1; k<N; k++) {
// (6*k-5)*(2*k-1)*(6*k-1)
v1 = 6*k-5;
mpf_mul_ui(v2.get_mpf_t(), v1.get_mpf_t(), 2*k-1);
mpf_mul_ui(v1.get_mpf_t(), v2.get_mpf_t(), 6*k-1); // v1 = (6*k-5)*(2*k-1)*(6*k-1)
// k*k*k*26680*640320*640320
v2 = k;
mpf_mul_ui(v3.get_mpf_t(), v2.get_mpf_t(), k);
mpf_mul_ui(v2.get_mpf_t(), v3.get_mpf_t(), k);
mpf_mul_ui(tmp1.get_mpf_t(), v2.get_mpf_t(), 26680); // tmp <= k*26680
mpf_mul_ui(v2.get_mpf_t(), tmp1.get_mpf_t(), 640320);
mpf_mul_ui(tmp1.get_mpf_t(), v2.get_mpf_t(), 640320);
// v2 <= v1/tmp = (6*k-5)*(2*k-1)*(6*k-1)/(k*k*k*26680*640320*640320)
mpf_div(v2.get_mpf_t(), v1.get_mpf_t(), tmp1.get_mpf_t());
mpf_neg(v1.get_mpf_t(), v2.get_mpf_t()); // v1 = -v1
mpf_mul(tmp1.get_mpf_t(), ak.get_mpf_t(), v1.get_mpf_t()); // tmp <= ak*v1
mpf_set(ak.get_mpf_t(), tmp1.get_mpf_t()); // ak = ak*v1
v1 = 545140134;
mpf_mul_ui(v2.get_mpf_t(), v1.get_mpf_t(), k); // v2 = 545140134*k
mpf_add_ui(v1.get_mpf_t(), v2.get_mpf_t(), 13591409); // v1 = 545140134*k + 13591409
mpf_mul(tmp1.get_mpf_t(), v1.get_mpf_t(), ak.get_mpf_t()); // tmp1 = v1*ak
mpf_add(v1.get_mpf_t(), tmp1.get_mpf_t(), pi.get_mpf_t()); // v1 = tmp1 + pi
mpf_set(pi.get_mpf_t(), v1.get_mpf_t()); // pi = v1
if (k % 5 == 0) {
// Release CPU when app is inactive, otherwise app will be killed by iOS
if ([[UIApplication sharedApplication] applicationState] != UIApplicationStateActive)
[NSThread sleepForTimeInterval:3];
}
}
mpf_sqrt_ui(d1.get_mpf_t(), 10005); // d1 = sqrt(10005)
mpf_mul(d.get_mpf_t(), d1.get_mpf_t(), pi.get_mpf_t()); // d = d1*pi
mpf_div_ui(d1.get_mpf_t(), d.get_mpf_t(), 4270934400); // d1 = d/4270934400
mpf_ui_div(d.get_mpf_t(), 1, d1.get_mpf_t()); // d = 1/d1
double diff = [[NSDate date] timeIntervalSinceDate:date1];
//gmp_printf("pi: %.*Ff\n", self.numDigits, d.get_mpf_t()); // Not works for big numbers, only for debugging
[self valueSave:d.get_mpf_t() time:diff];
NSLog(@"Done-pi, time = %.2f", diff);
self.totalTime = diff;
}
- (void)valueSave:(mpf_t)val time:(double)time{
NSString *docsDirectory = [NSSearchPathForDirectoriesInDomains(NSDocumentDirectory, NSUserDomainMask, YES) objectAtIndex:0];
NSString *name = [NSString stringWithFormat:@"value-%llu.txt", self.numDigits];
NSString *path = [docsDirectory stringByAppendingPathComponent:name];
FILE *fp = fopen ([path UTF8String], "w+");
char buf[255];
sprintf(buf, "Time: %fs\n", time);
fwrite(buf , sizeof(char), strlen(buf), fp);
mpf_out_str(fp, 10, 0, val); // 10-основание системы счисления
fclose(fp);
NSLog(@"Saved in: %@", path);
}
- (unsigned long int)getBitsSize {
// Calculate the number of bits, required to store numDigits (empiric way)
return (unsigned long int)(2.5*self.numDigits/log(2));
}
Для тех кто захочет поэкспериментировать самостоятельно, здесь выложен исходный код проекта для XCode. Конечно, приведенный выше алгоритм не идеален, его например вполне можно распараллелить хотя бы на 2 потока. Или даже попробовать использовать Accelerate Framework.
Результаты
При запуске на iPhone вылезли несколько забавных проблем. Первая — программа ни за что не хотела работать в бэкграунде, процесс вычислений просто останавливался. На тестовом iPhone 5S стояла iOS8, не знаю изменился ли принцип многозадачности в iOS9, но для 8ки решение оказалось простым — запустить GPS и подписаться на события от location service. При этом iOS «считает» что нам нужно постоянно получать координаты юзера, и позволяет программе работать даже в свернутом состоянии.
Вторая проблема вылезла минутой позже после первой. Как оказалось, iOS достаточно «умна», и считает подозрительным процесс, жрущий в фоне 100% ресурсов процессора. Видимо iOS считает что программа «повисла», и «убивает» ее примерно через минуту такой работы. Пришлось внутрь цикла вставить sleep с таким расчетом, чтобы «скважность» загрузки CPU была где-то 50/50. После этого программа могла считать и в фоновом режиме, хотя конечно скорость стала вдвое ниже. В итоге iPhone был просто подключен к зарядному устройству и оставлен на ночь, программа не закрывалась.
И наконец, обещанный результат: на iPhone 5S миллион знаков числа Пи вычислялись 49296 секунд, или около 14 часов. Кстати, на симуляторе с Core i7 время расчета составляет 4200 секунд, т.е. примерно в 11 раз быстрее. Интересно прикинуть, сколько будет вычисляться 100млн знаков. Оставляю это в качестве домашнего задания тем, кто дочитал до сюда. Также было бы интересно увидеть результаты для более новых (чем 5S) моделей iPhone. Программа во время расчетов показывает примерное время выполнения, результат сохраняется в папку iTunes file sharing.
Правка
В комментах подсказали сравнить программу с реализациями в Google Play. Как оказалось, там используется алгоритм Arithmetic-Geometric Mean (AGM), который действительно в разы быстрее. С последней версией вычисление миллиона знаков на iPhone 5S заняло 68 секунд.
Описание алгоритма и реализация на Python есть здесь: http://www.johndcook.com/blog/2012/06/03/calculating-pi-with-agm-and-mpmath/. C/С++ код для GMP доступен здесь: https://rosettacode.org/wiki/Arithmetic-geometric_mean/Calculate_Pi.
Тем кто захочет проверить
Зачем это надо?
Что касается мирового рекорда (который для десктопа составляет 5трлн знаков, правда и десктоп был не рядовым), то вряд ли его удастся побить на смартфоне. Да и подобной таблицы рекордов для смартфонов вроде еще никто не делал. Однако дело конечно не в рекорде — как можно видеть, подобные расчеты представляют собой достаточно интересную инженерную задачу, где остаются открытыми вопросы оптимизации и памяти, и скорости вычислений, и многопоточности. В общем, есть где «пошевелить мозгами», что как раз и наиболее интересно в программировании.