Всем доброго времени суток! Простым поиском я не сумел обнаружить упоминание модуля cvxpy и потому решил написать обучающий материал по нему – просто примеры кода, по которым в дальнейшем новичку будет проще использовать этот модуль для своих задач. cvxpy предназначен для решения задач оптимизации – нахождения минимумов/максимумов функций при определённых ограничениях. Если вам интересна эта тема – прошу под кат.

Здесь x – независимая переменная (в общем случае вектор), f(x)
целевая функция, которую нужно оптимизировать. Ограничения на область определения f(x) могут быть заданы при помощи равенств и неравенств.
Давайте рассмотрим следующую задачу линейного программирования:
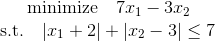
Если посмотреть на область, заданную неравенством с модулем, то можно увидеть что эта область легко может быть задана при помощи линейных неравенств:
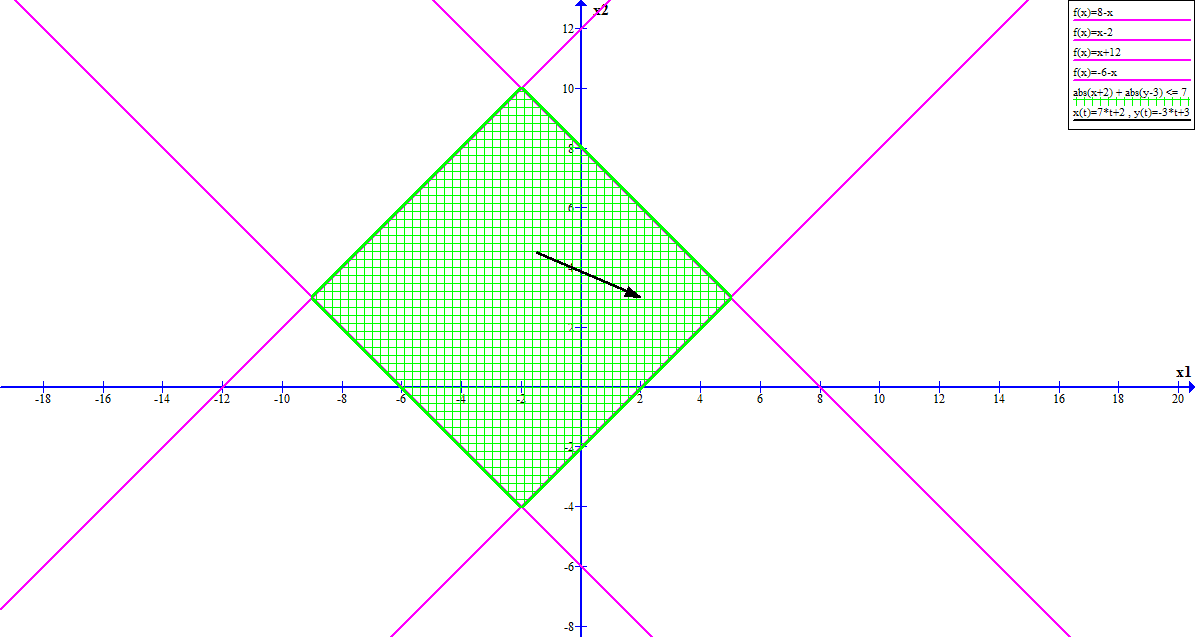
В нашем случае ограничения будут следующими:

О установке модуля подробно рассказано на сайте модуля. Давайте напишем простой код, который позволит нам решить нашу тестовую задачу оптимизации:
Наше текущее решение нецелое и выходит за ограничения, однако видно что оно лежит рядом с оптимальным решением (-9, 3). В cvxpy можно использовать разные решатели для решения задачи, подбирая лучший. Давайте попробуем GLPK:
Список доступных решателей возвращает функция
Можно решать не только задачи линейного программирования. Давайте рассмотрим исходную формулировку задачи:
Также можно искать решение для метода наименьших квадратов:
Конечно, некоторые задачи могут иметь тривиальное решение:
А некоторые могут не иметь решения вовсе:
Вот и всё. Можно узнать больше на сайте модуля.
Общая постановка задачи

Здесь x – независимая переменная (в общем случае вектор), f(x)
целевая функция, которую нужно оптимизировать. Ограничения на область определения f(x) могут быть заданы при помощи равенств и неравенств.
Пример задачи
Давайте рассмотрим следующую задачу линейного программирования:
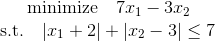
Если посмотреть на область, заданную неравенством с модулем, то можно увидеть что эта область легко может быть задана при помощи линейных неравенств:

В нашем случае ограничения будут следующими:

Решение задачи посредством cvxpy
О установке модуля подробно рассказано на сайте модуля. Давайте напишем простой код, который позволит нам решить нашу тестовую задачу оптимизации:
import numpy as np
import cvxpy as cvx
# наши независимые переменные
x = cvx.Variable(2)
A = np.array([[1, 1],
[1, -1],
[-1, 1],
[-1, -1]])
b = np.array([8, 2, 12, 6])
c = np.array([7, -3])
# ограничения
constraints = [A * x <= b]
# целевая функция и что с ней делать
obj = cvx.Minimize(c * x)
# формулируем задачу и решаем
prob = cvx.Problem(obj, constraints)
prob.solve()
print(prob.status) # optimal
print(prob.value) # -71.999999805
print(x.value) # [[-8.99999997] [ 3.00000002]]Наше текущее решение нецелое и выходит за ограничения, однако видно что оно лежит рядом с оптимальным решением (-9, 3). В cvxpy можно использовать разные решатели для решения задачи, подбирая лучший. Давайте попробуем GLPK:
prob.solve(solver = "GLPK")
print(prob.status) # optimal
print(prob.value) # -72.0
print(x.value) # [[-9.] [ 3.]]Список доступных решателей возвращает функция
installed_solvers().Другие примеры
Можно решать не только задачи линейного программирования. Давайте рассмотрим исходную формулировку задачи:
# ограничения
constraints = [cvx.abs(x[0] + 2) + cvx.abs(x[1] - 3) <= 7]
# целевая функция и что с ней делать
obj = cvx.Minimize(c * x)
# формулируем задачу и решаем
prob = cvx.Problem(obj, constraints)
prob.solve(solver = "GLPK")
print(prob.status) # optimal
print(prob.value) # -72.0
print(x.value) # [[-9.] [ 3.]]Также можно искать решение для метода наименьших квадратов:
# целевая функция и что с ней делать
obj = cvx.Minimize(cvx.norm(A * x - b)) # по умолчанию используется вторая норма
# формулируем задачу и решаем
prob = cvx.Problem(obj)
prob.solve()
print(prob.status) # optimal
print(prob.value) # 13.9999999869
print(x.value) # [[-2.] [ 3.]]Конечно, некоторые задачи могут иметь тривиальное решение:
A = np.array([[1, 1],
[1, -1],
[-1, 1]])
b = np.array([8, 2, 12])
c = np.array([7, -3])
# ограничения
constraints = [A * x <= b]
# целевая функция и что с ней делать
obj = cvx.Minimize(c * x)
# формулируем задачу и решаем
prob = cvx.Problem(obj, constraints)
prob.solve()
print(prob.status) # unbounded
print(prob.value) # -inf
print(x.value) # NoneА некоторые могут не иметь решения вовсе:
A = np.array([[1, 1],
[1, -1],
[-1, 1],
[-1, -1]])
b = np.array([-6, -12, -2, -8])
# ограничения
constraints = [A * x <= b]
# целевая функция и что с ней делать
obj = cvx.Minimize(c * x)
# формулируем задачу и решаем
prob = cvx.Problem(obj, constraints)
prob.solve()
print(prob.status) # infeasible
print(prob.value) # inf
print(x.value) # NoneВот и всё. Можно узнать больше на сайте модуля.