 Создатели шаблонов в C++ заложили основу целого направления для исследований и разработки: оказалось, что язык шаблонов C++ обладает полнотой по Тьюрингу, то есть метапрограммы (программы, предназначенные для работы на этапе компиляции) C++ в состоянии вычислить всё вычислимое. На практике мощь шаблонов чаще всего применяется при описании обобщенных структур данных и алгоритмов: STL (Standard Template Library) тому живой пример.
Создатели шаблонов в C++ заложили основу целого направления для исследований и разработки: оказалось, что язык шаблонов C++ обладает полнотой по Тьюрингу, то есть метапрограммы (программы, предназначенные для работы на этапе компиляции) C++ в состоянии вычислить всё вычислимое. На практике мощь шаблонов чаще всего применяется при описании обобщенных структур данных и алгоритмов: STL (Standard Template Library) тому живой пример.Однако, с приходом C++11 с его
variadic-шаблонами, библиотекой type_traits, кортежами и constexpr'ами метапрограммирование стало более удобным и наглядным, открыв дорогу к реализации многих идей, которые раньше можно было воплотить только с помощью расширений конкретного компилятора или сложных многоэтажных макросов.В данной статье будет разработана реализация бинарного дерева поиска времени компиляции: структуры данных, являющейся логическим «расширением» кортежа. Мы воплотим бинарное дерево в виде шаблона и попрактикуемся в метапрограммировании: переносе рекурсивных и не только алгоритмов на язык шаблонов C++.
Содержание
- Немного теории
- Разминка: операции с кортежами и превращение числа в класс
- Бинарное дерево поиска
- Применение
- Что потом?
- Литература
Немного теории
Для начала вспомним некоторые определения и понятия о структурах данных и алгоритмах. Можно пропустить этот раздел и сразу перейти к деталям реализации, если читатель знаком с основами теории графов и/или представляет, что такое бинарные деревья и как их можно готовить.
Определения и не только:
Свободное дерево (дерево без выделенного корня) или просто дерево — ациклический неориентированный граф.
Дерево с корнем — свободное дерево, в котором выделена одна вершина, называемая корнем (root).
Узлы (nodes) — вершины дерева с корнем.
Родительский узел или родитель узла X — последний узел, предшествующий X на пути от корня R к этому узлу X. В таком случае узел X называется дочерним к описанному родительскому узлу Y. Корень дерева не имеет родителя.
Лист — узел, у которого нет дочерних узлов.
Внутренний узел — узел, не являющийся листом.
Степень узла X — количество дочерних узлов этого узла X.
Глубина узла X — длина пути от корня R к этому узлу X.
Высота узла (height) — длина самого длинного простого (без возвратов) нисходящего пути от узла к листу.
Высота дерева — высота корня этого дерева.
Упорядоченное дерево — дерево с корнем, в котором дочерние узлы каждого узла упорядочены (т.е. задано отображение множества дочерних узлов на множество натуральных чисел от 1 до k, где k — общее количество дочерних узлов этого узла). Простыми словами, каждому дочернему узлу присвоено имя: «первый», «второй», ..., "k-тый".
Бинарное дерево (binary tree) — (рекурсивно) либо пустое множество (не содержит узлов), либо состоит из трёх непересекающихся множеств узлов: корневой узел, бинарное дерево, называемое левым поддеревом, и бинарное дерево, называемое правым поддеревом. Таким образом, бинарное дерево — это упорядоченное дерево, у которого каждый узел имеет степень не более 2 и имеет «левый» и/или/либо «правый» дочерние узлы.
Полностью бинарное дерево (full binary tree) — бинарное дерево, у которого каждый узел либо лист, либо имеет степень два. Полностью бинарное дерево можно получить из бинарного добавлением фиктивных дочерних листов каждому узлу степени 1.
Бинарное дерево поиска — связанная структура данных, реализованная посредством бинарного дерева, каждый узел которого может быть представлен объектом, содержащим ключ (key) и сопутствующие данные, ссылки на левое и правое поддеревья и ссылку на родительский узел. Ключи бинарного дерева поиска удовлетворяют свойству бинарного дерева поиска:
Обход дерева — формирование списка узлов, порядок определяется типом обхода.
Дерево с корнем — свободное дерево, в котором выделена одна вершина, называемая корнем (root).
Узлы (nodes) — вершины дерева с корнем.
Родительский узел или родитель узла X — последний узел, предшествующий X на пути от корня R к этому узлу X. В таком случае узел X называется дочерним к описанному родительскому узлу Y. Корень дерева не имеет родителя.
Лист — узел, у которого нет дочерних узлов.
Внутренний узел — узел, не являющийся листом.
Степень узла X — количество дочерних узлов этого узла X.
Глубина узла X — длина пути от корня R к этому узлу X.
Высота узла (height) — длина самого длинного простого (без возвратов) нисходящего пути от узла к листу.
Высота дерева — высота корня этого дерева.
Упорядоченное дерево — дерево с корнем, в котором дочерние узлы каждого узла упорядочены (т.е. задано отображение множества дочерних узлов на множество натуральных чисел от 1 до k, где k — общее количество дочерних узлов этого узла). Простыми словами, каждому дочернему узлу присвоено имя: «первый», «второй», ..., "k-тый".
Бинарное дерево (binary tree) — (рекурсивно) либо пустое множество (не содержит узлов), либо состоит из трёх непересекающихся множеств узлов: корневой узел, бинарное дерево, называемое левым поддеревом, и бинарное дерево, называемое правым поддеревом. Таким образом, бинарное дерево — это упорядоченное дерево, у которого каждый узел имеет степень не более 2 и имеет «левый» и/или/либо «правый» дочерние узлы.
Полностью бинарное дерево (full binary tree) — бинарное дерево, у которого каждый узел либо лист, либо имеет степень два. Полностью бинарное дерево можно получить из бинарного добавлением фиктивных дочерних листов каждому узлу степени 1.
Бинарное дерево поиска — связанная структура данных, реализованная посредством бинарного дерева, каждый узел которого может быть представлен объектом, содержащим ключ (key) и сопутствующие данные, ссылки на левое и правое поддеревья и ссылку на родительский узел. Ключи бинарного дерева поиска удовлетворяют свойству бинарного дерева поиска:
если X — узел, и узел Y находится в левом поддереве X, то Y.key ≤ X.key. Если узел Y находится в правом поддереве X, то X.key ≤ Y.key.Подразумевается, что мы умеем сравнивать ключи (на множестве значений ключа задано транзитивное отношение порядка, т.е. проще говоря операция «меньше») и говорить о равенстве ключей. В реализации без ограничения общности мы будем оперировать строгими неравенствами порядка, используя только операцию "<" и "==", построенную на её основе из соотношения
Обход дерева — формирование списка узлов, порядок определяется типом обхода.
Разминка: операции с кортежами и превращение числа в класс
Прежде чем окунуться с головой в рекурсивные дебри и насладиться буйством угловых скобок, поупражняемся в написании метафункций. Далее нам понадобятся функции конкатенации кортежей и функция добавления типа в существующий кортеж:
template <class U, class V>
struct tuple_concat;
template <class Tuple, class T>
struct tuple_push;
Об операциях над типами:
Разумеется, ни о каких «конкатенации» и «добавлении» типов в «контейнеры типов» речи не идёт. Это общая и важная особенность мира времени компиляции: определенный тип (класс) никаким образом модифицировать уже невозможно, но возможно определить новый (или среди ранее определенных выбрать существующий) тип, имеющий необходимые нам свойства.
Стандарт C++11 вводит заголовочный файл
Стандарт C++11 вводит заголовочный файл
type_traits (как часть библиотеки поддержки типов), содержащий коллекцию полезных метафункций. Все они являются шаблонами структур, и после инстанцирования определяют локально некий тип type или числовую константу value (или ничего, как в случае отключения перегрузки с использованием std::enable_if). Мы будем придерживаться тех же принципов проектирования метафункций.Первая функция принимает в качестве аргументов шаблона два кортежа, вторая — кортеж и тип, который необходимо добавить в кортеж. Подстановка в качестве аргументов неподходящих типов (например, при попытке сделать конкатенацию
int и float) — операция бессмысленная, поэтому базовый шаблон этих структур не определяется (это предотвратит его инстанцирование для произвольных типов), а вся полезная работа делается в частичных специализациях:template <template <class...> class T, class... Alist, class... Blist>
struct tuple_concat<T<Alist...>, T<Blist...>> { using type = T<Alist..., Blist...>; };
template <template <class...> class Tuple, class... Args, class T>
struct tuple_push<Tuple<Args...>,T> { using type = Tuple<Args..., T>; };
Примерный перевод на человеческий язык специализации
tuple_concat:Если в качестве аргументов шаблона выступают два класса, которые в свою очередь являются результатами инстанцирования одного и того же шаблона класса (
T) с переменным числом аргументов, и они были инстанцированы с parameter pack'ами Alist и Blist, то определить локально псевдоним type как инстанцированую версию того же шаблона класса T с конкатенированным списком аргументов, т.е. T<Alist..., Blist...>.О терминологии:
Далее в статье часто будут отождествляться понятия «инстанцирование шаблона структуры метафункции» (правильнее и мудрёнее) и «вызов метафункции» (короче и нагляднее), по сути обозначающие одно и то же: «в этом месте программы из шаблона произойдёт генерация структуры со всеми вытекающими последствиями: она приобретёт размер, внутри определятся псевдонимы и классы и т.д. и т.п.»
Звучит зловеще, но на практике всё проще, чем кажется: при попытке вызвать
tuple_concat с двумя кортежами одного вида (например, с двумя std::tuple), внутри структуры определится тип того же кортежа со «сшитым» списком аргументов входных кортежей. Иные попытки инстанцирования просто не скомпилируются (компилятор не сможет вывести типы для определенной выше частичной специализации, а инстанцирование общего шаблона окажется невозможным ввиду отсутствия его тела). Пример:using t1 = std::tuple<char,int>;
using t2 = std::tuple<float,double>;
using t3 = std::tuple<char,int,float,double>;
using conc = typename tuple_concat<t1,t2>::type;
// using err = typename tuple_concat<int,bool>::type; // ошибка
static_assert(std::is_same<t3,conc>::value, ""); // утверждение истинно, типы одинаковы
В свете вышесказанного рассмотрение специализации
tuple_push не должно составить большого труда. Дополнительно, для удобства определим соответственные псевдонимы шаблонов:template <typename U, typename V>
using tuple_concat_t = typename tuple_concat<U,V>::type;
template <typename Tuple, typename T>
using tuple_push_t = typename tuple_push<Tuple,T>::type;
Эта удобная возможность появилась в языке в C++11 стандарте: она, например, позволяет для доступа к
type вместо заковыристого typename tuple_concat<t1,t2>::type писать просто tuple_concat_t<t1,t2>.О конкатенации:
Стандартный заголовок
tuple содержит определение (не мета-)функции tuple_cat(), конструирующей кортеж посредством конкатенации неопределенного числа std::tuple'ей, переданных в качестве аргументов. Внимательный читатель может заметить, что tuple_concat может быть проще реализована посредством вывода типа результата decltype(tuple_cat(...)), однако, во-первых, полученная выше реализация не ограничена типом кортежа std::tuple, а во-вторых, это было разминочным упражнением для постепенного погружения в более сложную арифметику типов.Последние приготовления: не для дела, а для
/// Модно-молодёжно STL-like путём
template<size_t number>
struct num_t : std::integral_constant<size_t, number> {};
// ИЛИ классически определим внутренность руками
template<size_t number>
struct num_t { enum : size_t { value = number } };
Смысл у обоих определений один: инстанцирование шаблона с различными численными аргументами будет приводить к определению различных типов:
num_t<0>, num_t<13>, num_t<42> и т.д. Не более чем для удобства наделим эту структуру статическим числовым значением value, что позволит нам явно получать назад число из аргумента шаблона (посредством доступа some_num_type::value) без прибегания к выводу типа.Бинарное дерево поиска
Рекурсивное определение бинарного дерева поиска оказывается удобным для непосредственного воплощения в виде шаблона. Упрощенное определение
ДЕРЕВО : NIL | [ДЕРЕВО, ДАННЫЕ, ДЕРЕВО]
можно перефразировать как «дерево — ЭТО пустое множество ИЛИ множество из трёх элементов: дерево (т.н. левое поддерево), данные, дерево (т.н. правое поддерево)».
Помимо этого, как уже упоминалось, бинарное дерево поиска требует задания отношения порядка на множестве значений, хранящихся в узлах дерева (мы должны уметь как-то сравнивать и упорядочивать узлы, т.е. иметь операцию «меньше»). Каноничным подходом является разбиение данных узла на ключ и значение (ключи сравниваем, значения просто храним), но в нашей реализации в целях упрощения структуры без ограничения общности будем считать данные узла единым типом, для задания же отношения порядка воспользуемся специальным типом
Comp (comparator, поговорим о нём далее)./// Пустое множество
struct NIL {};
/// Узел
template<typename T, typename Left, typename Right, typename Comp>
struct node {
using type = T; // node value
using LT = Left; // left subtree
using RT = Right; // right subtree
using comp = Comp; // types comparator
};
/// Лист: узел без потомков (псевдоним шаблона)
template <typename T, typename Comp>
using leaf = node<T,NIL,NIL,Comp>;
Несмотря на то, что отношение порядка всё-таки задано на множестве хранимых в узлах типов, удобно приписать его самому дереву и хранить как часть типа этого дерева: при вызове метафункций поиска, вставки и обхода непустого дерева нет необходимости в дополнительном указании компаратора.
Об отцах и детях:
Внимательный читатель обратит внимание на то, что в представленной структуре не хватает одного важного для реализации большинства алгоритмов элемента: ссылки на родительский узел (в нашем случае — псевдонима типа родительского дерева). Заметив это и попытавшись исправить эту несправедливость, читатель рано или поздно в ужасе осознает, что в данном случае будет иметь место циклическая зависимость псевдонимов.
Сама по себе ситуация не критичная и имеет обходное решение в виде разделения объявлений и определений типов:
Сама по себе ситуация не критичная и имеет обходное решение в виде разделения объявлений и определений типов:
template<...>
struct one {
struct two;
using three = one<two, ...>;
struct two : one<three, ...> {};
};
Примечание: экспериментальным путём обнаружено, что такие структуры компилируются и инстанцируются современными gcc и clang, тем не менее, я пока не проверял строгое соответствие стандарту объявлений таких необычных шаблонов.Однако на практике работать с такими сущностями и создавать их оказывается очень, ОЧЕНЬ сложно. Обратная ссылка на родительский элемент производит интересный эффект: фактически наше «односвязное дерево» превращается в настоящий граф (вкусно!), который при любой модификации должен инстанцировать себя «единовременно», заново и полностью (грустно). Более глубокий анализ данной ситуации выходит за рамки настоящей статьи и входит в число моих дальнейших планов по исследованию возможностей метапрограммирования в C++.
Это не единственный способ реализации и представления дерева (например, можно хранить узлы в кортеже и проводить их индексацию), однако такое описание более наглядно и удобно для непосредственного применения алгоритмов работы с деревом.
Отношение порядка
Структура
Comp должна содержать метафункции сравнения типов (т.е. шаблоны операций «меньше» и «равно»). Напишем пример такого сравнителя, основанного на sizeof'ах типов (возможно, единственная числовая характеристика, определенная для всех полных типов):struct sizeof_comp {
template <typename U, typename V>
struct lt : std::integral_constant<bool, (sizeof(U) < sizeof(V))> {}; // меньше
template <typename U, typename V>
struct eq : std::integral_constant<bool, (sizeof(U) == sizeof(V))> {}; // равно
};
Здесь всё должно быть прозрачно:
lt — метафункция «меньше» для типов, eq — метафункция «равно». Использован подход, показанный ранее для определения типов чисел: наследование от std::integral_constant наделит инстанцированные lt и eq статическими булевыми значениями value.На практике конкретные деревья конкретных типов должны снабжаться сравнителем, специфичным для данной задачи. Например, напишем сравнитель для описанного ранее класса «числовых типов»:
struct num_comp {
template <typename U, typename V>
struct lt : std::integral_constant<bool, (U::value < V::value)> {};
template <typename U, typename V>
struct eq : std::integral_constant<bool, (U::value == V::value)> {};
};
Такой компаратор, вообще говоря, универсален и умеет сравнивать любые типы, содержащие статическое значение
value.О генерации компаратора посредством CRTP:
Ранее в теоретическом разделе упоминалось, что операции «меньше», вообще говоря, достаточно, чтобы интуитивно определить и операцию «равно». Используем подход аналогичный CRTP (Curiously recurring template pattern), чтобы определить полный компаратор на основе только компаратора, содержащего операцию (метафункцию) «меньше»:
/// Шаблон для базового класса всех сгенерированных компараторов
template <typename lt_traits>
struct eq_comp {
template <typename U, typename V>
struct lt : std::integral_constant<bool, lt_traits::template lt<U,V>::value> {};
template <typename U, typename V>
struct eq : std::integral_constant<bool, (!lt<U,V>::value && !lt<V,U>::value)> {};
};
/// Переписаный компаратор sizeof, наследование наделит его метафункцией eq_comp::eq
struct sizeof_comp : public eq_comp<sizeof_comp> {
template <typename U, typename V>
struct lt : std::integral_constant<bool, (sizeof(U) < sizeof(V))> {};
};
/// Переписаный компаратор num_t
struct num_comp : public eq_comp<num_comp> {
template <typename U, typename V>
struct lt : std::integral_constant<bool, (U::value < V::value)> {};
};
Теперь у нас есть всё для того, чтобы явно, «руками», определить первое дерево типов:
using t1 = node<
num_t<5>,
node<
num_t<3>,
leaf<num_t<2>>,
leaf<num_t<4>>
>,
node<
num_t<7>,
NIL,
leaf<num_t<8>>
>
>;
Примечание: Здесь и далее в примерах по-умолчанию подразумевается сравнительnum_comp, явное указание его в списке аргументов шаблонов опускается. Вообще, после разработки операцииinsertнам не придётся строить деревья таким образом (явным определением).
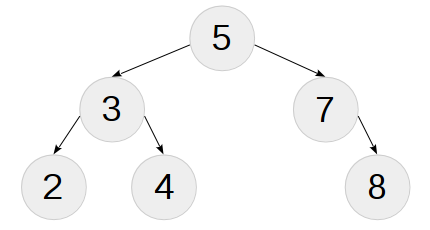
Об отладке на этапе компиляции:
Как нам убедиться, что определенный нами класс точно описывает то, что мы задумали?
Эта отдельная интересная тема для дискуссии и исследования — отладка метапрограмм. У нас нет ни стека вызовов, ни переменных, ни, чёрт возьми, банального
Не будем здесь касаться вопроса многомегабайтных сообщений об ошибках просто в случае некорректной программы: после некоторой практики это перестаёт быть проблемой, так как в подавляющем большинстве случаев лишь первая ошибка инстанцироания ведёт к каскаду дальнейших ошибок: отладка в таком случае ведётся «методом последовательных приближений».
Но, как бы парадоксально это ни звучало, что делать, если программа скомпилировалось успешно? Здесь уже автор более свободен в выборе методов отладки. Тип результата метафункций наподобие определенных в
Библиотека деревьев содержит такой принтер и примеры его использования, читатель может ознакомиться с ними по ссылке на github в конце статьи. Вот, например, напечатанное дерево из примера выше:
Эта отдельная интересная тема для дискуссии и исследования — отладка метапрограмм. У нас нет ни стека вызовов, ни переменных, ни, чёрт возьми, банального
printf/std::cout. Есть техники, позволяющие печатать внутри сообщений об ошибках компилятора удобочитаемые выведенные типы, и, в принципе, это достаточно полезная возможность проверки сгенерированных структур (например, после модификации дерева).Не будем здесь касаться вопроса многомегабайтных сообщений об ошибках просто в случае некорректной программы: после некоторой практики это перестаёт быть проблемой, так как в подавляющем большинстве случаев лишь первая ошибка инстанцироания ведёт к каскаду дальнейших ошибок: отладка в таком случае ведётся «методом последовательных приближений».
Но, как бы парадоксально это ни звучало, что делать, если программа скомпилировалось успешно? Здесь уже автор более свободен в выборе методов отладки. Тип результата метафункций наподобие определенных в
type_traits можно просто печатать в виде typeid(t).name() (начиная с C++11 можно легально подсматривать в RTTI). Простые структуры данных можно выводить на экран специальными метафункциями с хвостовой рекурсией, для сложных придётся городить «принтеры», сопоставимые по сложности с операциями над самой структурой.Библиотека деревьев содержит такой принтер и примеры его использования, читатель может ознакомиться с ними по ссылке на github в конце статьи. Вот, например, напечатанное дерево из примера выше:
/--{2}
/--{3}--<
\--{4}
--{5}---<
\--{7}--\
\--{8}
Высота
Посмотрим на рекурсивную функцию вычисления высоты бинарного дерева:
/// Вход: T - дерево, выход: h - высота
ВЫСОТА(T):
ЕСЛИ T == NIL
ВЫВОД 0
ИНАЧЕ
ВЫВОД 1 + MAX(ВЫСОТА(T.LEFT), ВЫСОТА(T.RIGHT))
Она прекрасна. Просто берём и переносим эту функцию на C++:
/// Объявление общего шаблона
template <typename Tree>
struct height;
/// Частичная специализация: "ЕСЛИ T == NIL"
template <>
struct height<NIL> : std::integral_constant<size_t, 0> {};
/// Определение общего шаблона (рекурсивное)
template <typename Tree>
struct height {
static constexpr size_t value = 1 + max(
height<typename Tree::LT>::value,
height<typename Tree::RT>::value
);
};
Примечание: мы сознательно пошли на небольшое упрощение, из-за которого вычисленная высота дерева будет на 1 больше её математического определения (высота пустого множества не определена). Читатель без труда сможет исправить при необходимости эту особенность, добавив ещё один уровень косвенности и явно вычитая 1 из результата вызова метафункции, однако тогда придётся запретить инстанцирование height для пустого дерева.Код достаточно прост: при попытке вызова height с пустым множеством будет инстанцирована соответствующая специализация, содержащая статическое value = 0, в противном случае продолжится каскад инстанцирований, пока мы не наткнёмся на пустое поддерево (то есть тот же самый NIL), на котором рекурсия и остановится. Это характерная особенность реализации рекурсивных функций посредством шаблонов C++: мы обязаны специализировать дно рекурсии, иначе каскад инстанцирований либо не остановится (компилятор выдаст ошибку о превышении лимита вложенных инстанцирований), либо на одном из шагов произойдёт попытка доступа к несуществующему члену или значению в классе (без специализации описанная выше функция в определенный момент не смогла бы получить Tree::LT, когда Tree было бы равно пустому поддереву NIL).В коде выше используется функция
max. Она должна быть constexpr (или просто метафункцией, тогда её вызов немного изменится), пример простой и известной реализации:template <typename T> constexpr T max(T a, T b) { return a < b ? b : a; }Наконец, использование функции
height:static_assert(height<t1>::value == 3, "");Скажем о «сложности» функции
height: требуется n инстанцирований, где n — число узлов дерева; глубина инстанцирования равна h — т.е. высоте дерева.Какая ещё сложность и зачем она здесь?!
Дело в том, что, хотя всю работу по рекурсивному вычислению делает компилятор, его мощь не безгранична: с лёгкой руки изобретателей шаблонов наделённый обязанностью решать проблему останова (!), компилятор всё-таки должен контролировать своё собственное состояние и не вдаваться в крайности, занимаясь майнингом биткоинов сумасшедшего метапрограммиста. А если серьёзно, компилятор сам должен уметь остановиться: для этого вводятся ограничения на глубину инстанцирований шаблонов, рекурсивных вызовов
В документации к своему любимому компилятору читатель сможет найти конкретные значения: например, gcc-5.4 «из коробки» (без дополнительных опций) инстанцирует шаблоны не глубже 900 уровней. В свете вышесказанного это означает, что нельзя забывать об оптимизации метафункций (как бы дико это ни звучало). Например, вызов
Например, в стандарте C++14 планируется ввести шаблон для генерации целочисленных последовательностей (
Если превышение допустимой глубины инстанцирований может просто помешать компиляции, то количество инстанцирований (т.е. вызовов метафункций) прямо влияет на время компиляции: для сложных метапрограмм оно может оказать весьма велико. Здесь играет роль множество факторов (необходимость вывода типов, сопоставление частичных специализаций и т.д.), посему не стоит забывать, что компилятор — такая же программа, а механизм шаблонов — своего рода API к внутреннему кодогенератору компилятора, и пользоваться им надо учиться так же, как осваивать отдельный язык программирования — последовательно и аккуратно (и чтобы никаких «Курсов программирования для чайников за 24 часа»!).
constexpr-функций и длину variadic-списков аргументов.В документации к своему любимому компилятору читатель сможет найти конкретные значения: например, gcc-5.4 «из коробки» (без дополнительных опций) инстанцирует шаблоны не глубже 900 уровней. В свете вышесказанного это означает, что нельзя забывать об оптимизации метафункций (как бы дико это ни звучало). Например, вызов
height вполне может отказаться компилироваться gcc, если дерево имеет высоту > 900. Можно даже ввести O-нотацию для описания сложности (хотя часто можно точно посчитать число и глубину инстанцирований), и она будет иметь вполне здравый смысл.Например, в стандарте C++14 планируется ввести шаблон для генерации целочисленных последовательностей (
std::integer_sequence): прямая рекурсивная реализация требует N инстанцирований для последовательности 0..N-1, однако существуют элегантные древоподобные решения, глубина рекурсии которых растёт со скоростью логарифма от длины последовательности. В конце концов, мы всегда можем реализовать любую функцию полным перебором, но компилятор этому точно не обрадуется (как и мы, час ждущие завершения компиляции 30-строчной программы или вынужденные читать 9000-страничные сообщения об ошибках).Если превышение допустимой глубины инстанцирований может просто помешать компиляции, то количество инстанцирований (т.е. вызовов метафункций) прямо влияет на время компиляции: для сложных метапрограмм оно может оказать весьма велико. Здесь играет роль множество факторов (необходимость вывода типов, сопоставление частичных специализаций и т.д.), посему не стоит забывать, что компилятор — такая же программа, а механизм шаблонов — своего рода API к внутреннему кодогенератору компилятора, и пользоваться им надо учиться так же, как осваивать отдельный язык программирования — последовательно и аккуратно (и чтобы никаких «Курсов программирования для чайников за 24 часа»!).
Обход центрированный (in-order traversal)
Задача обхода — определенным образом сформировать список узлов (или данных из узлов, вопрос терминологии и имеет значение на практике). Центрированный (симметричный) обход — обход, при котором корень дерева занимает место между результатами соответствующих обходов левого и правого поддеревьев. Вместе со свойством бинарного дерево поиска (которое о неравенствах, см. теорию) это говорит о том, что центрированный обход бинарного дерева поиска сформирует нам отсортированный список узлов — круто! Вот как будет выглядеть обход определенного ранее дерева:

Рекурсивный алгоритм обхода довольно прост:
/// Вход: T - дерево, выход: w - список данных из узлов in-order обхода
INORDER(T):
ЕСЛИ T == NIL
ВЫВОД {}
ИНАЧЕ
ВЫВОД INORDER(T.LEFT) + {T.KEY} + INORDER(T.RIGHT)
Операция "+" в данном случае обозначает конкатенацию списков. Да-да, это именно то, ради чего мы реализовывали конкатенацию кортежей, так как кортежи — это наши списки типов на этапе компиляции. И снова — просто берём и пишем код:
/// Объявление общего шаблона
template <typename Tree>
struct walk;
/// Частичная специализация: "ЕСЛИ T == NIL"
template <>
struct walk<NIL> { using type = std::tuple<>; };
/// Определение общего шаблона (рекурсивное)
template <typename Tree>
struct walk {
private:
// обход левого поддерева
using accL = typename walk<typename Tree::LT>::type;
// добавляем корень
using accX = tuple_push_t<accL, typename Tree::type>;
// конкатенируем с обходом правого поддерева
using accR = tuple_concat_t<accX, typename walk<typename Tree::RT>::type>;
public:
// результат
using type = accR;
};
В данном случае не более чем ради наглядности мы воспользовались локальными
private псевдонимами: все псевдонимы можно подставить друг в друга и получить фарш, обфусцированный похлеще случайно сгенерированной строки, и даже отступы нас не спасут. Но мы же стараемся для людей, не так ли?Сложность функции
walk: O(n) инстанцирований, где n — число узлов дерева (O-нотация использована для упрощения: аккуратный подсчёт даст примерно 3n вызовов метафункций с учётом конкатенаций). Приятно, что функции tuple_concat и tuple_push выполняют свою работу за 1 инстанцирование, так как они не рекурсивны (благодаря возможности вывода типов parameter pack'ов). Глубина инстанцирований, как и в случае height, равна h — высоте дерева.О читаемости кода:
Не ленитесь добавлять синтаксический сахар и аккуратно форматировать код: метапрограммы объективно воспринимаются хуже, чем обычный код, поэтому стандартные требования к облагораживанию кода ещё более актуальны в этом деле.
Ещё одно замечание по написанию метафункций: читатель, возможно, обратил внимание на то, что для последних двух функций нет необходимости разделять объявление и определение общего шаблона. Это так, однако я придерживаюсь стандартизированного подхода: «от максимально частного к максимально общему». Многие шаблоны целиком работают на частичных специализациях, и в таком случае очень удобно оказывается описывать эти специализации с возрастающим уровнем общности: мысленно программист проходит тот же путь, какой проходит компилятор в попытках инстанцирования и вывода типов.
Ещё одно замечание по написанию метафункций: читатель, возможно, обратил внимание на то, что для последних двух функций нет необходимости разделять объявление и определение общего шаблона. Это так, однако я придерживаюсь стандартизированного подхода: «от максимально частного к максимально общему». Многие шаблоны целиком работают на частичных специализациях, и в таком случае очень удобно оказывается описывать эти специализации с возрастающим уровнем общности: мысленно программист проходит тот же путь, какой проходит компилятор в попытках инстанцирования и вывода типов.
Поиск
Поиск по ключу является основной операцией в классических бинарных деревьях поиска (название говорит само за себя). Мы решили не разделять ключ и данные, поэтому для сравнения узлов будем применять введённый сравнитель
Comp. Рекурсивный алгоритм поиска:/// Вход: T - дерево, k - тип-ключ, /// выход: N - узел, содержащий тип k` == k в терминах сравнителя
SEARCH(T,k):
ЕСЛИ T == NIL ИЛИ k == T.KEY
ВЫВОД T
ИНАЧЕ
ЕСЛИ k < T.KEY
ВЫВОД SEARCH(T.LEFT, k)
ИНАЧЕ
ВЫВОД SEARCH(T.RIGHT, k)
Реализация внешне похожа на разработанные ранее:
/// Объявление общего шаблона
template <typename Tree, typename T>
struct search;
/// Специализация для пустого дерева
template <typename T>
struct search<NIL,T> { using type = NIL; };
/// Определение общего шаблона
template <typename Tree, typename T>
struct search {
using Comp = typename Tree::comp;
using type = typename std::conditional<
Comp::template eq<T, typename Tree::type>::value, // k == T.KEY ?
Tree, // поиск завершен, иначе:
typename std::conditional<
Comp::template lt<T, typename Tree::type>::value, // k < T.KEY ?
typename search<typename Tree::LT, T>::type, // тогда ищем в левом
typename search<typename Tree::RT, T>::type // иначе -- в правом
>::type
>::type;
};
Выглядит несколько сложнее, это неспроста: во-первых, сам алгоритм содержит больше ветвлений (больше сравнений и условий), во-вторых, здесь мы уже должны применять определенное ранее отношение порядка, и на его основе продолжать поиск рекурсивно либо в левом, либо в правом поддереве. Обратим внимание на детали:
- Для сравнения типов используется сравнитель из корня дерева:
Tree::comp, что логично: отношение порядка определяет как способ построения дерева, так и последующие операции (в том числе, поиск), вот почему было удобно поместить псевдоним сравнителя прямо внутрь шаблона дерева (node<>). - Для доступа к шаблону, зависящему от аргумента шаблона (
Tree::comp::eq<...>иTree::comp::lt<...>), необходимо использовать ключевое словоtemplate. - Мы пошли по пути наименьшего сопротивления и использовали
std::conditional— стандартную метафункцию, определяющую результирующий псевдоним в зависимости от булевой переменной (такой аналог тернарного оператора ?: для типов). Почему это может быть не очень хорошо — см. далее, однако из положительных моментов — большая наглядность.
Сложность такой реализации
search — опять-таки O(n) инстанцирований, глубина — h (высота дерева). «Стоп!» — воскликнет удивленный читатель, — «а как же логарифмическая сложность поиска и всё такое?»Тут-то и летят камни в сторону
std::conditional и выявляется его принципиальное отличие от оператора ?:: тернарный оператор не вычисляет то выражение, которое не будет его результатом (например, мы можем с чистой совестью разыменовывать нулевой указатель в одном из двух выражений, которое отбросится при проверке этого указателя в первом аргументе оператора). std::conditional же инстанцирует все три аргумента (как обычная метафункция), именно поэтому одного только std::conditional недостаточно для остановки рекурсии, и мы всё ещё должны специализировать дно рекурсии.Прямой результат — лишние инстанцирования, захватывающие всё дерево целиком от корня до листьев. Особым колдунством с добавлением ещё одного уровня косвенности можно-таки «отключить» на каждом шаге рекурсии инстанцирования по пути поддерева, в котором точно нет искомого узла (написав ещё пачку специализаций для этого уровня косвенности), и добиться заветной сложности O(h), однако, на мой взгляд, это задача для более глубокого исследования и в данном случае будет являться преждевременной оптимизацией.
Примеры применения (использованы шаблоны псевдонимов, больше примеров см. в репозитории):
using found3 = search_t<NIL, num_t<0>, num_comp>; // в пустом дереве
using found4 = search_t<t1, num_t<5>, num_comp>; // значение в корне
using found5 = search_t<t1, num_t<8>, num_comp>; // значение в листе
static_assert(std::is_same<found3, NIL>::value, ""); // не найдено
static_assert(std::is_same<found4, t1>::value, ""); // само дерево
static_assert(std::is_same<found5, leaf<num_t<8>>>::value, ""); // лист
Это может показаться странным: мы ищем в дереве узел с типом… который фактически уже указан в качестве аргумента — зачем? На самом деле, ничего необычного в этом нет — мы ищем тип, равный аргументу в терминах сравнителя. Деревья STL (
std::map) тоже хранят в узлах пары (std::pair), и первый элемент пары считается ключом, который, собственно, и участвует в сравнениях. Достаточно хранить в нашем дереве ту же std::pair и заставить сравнитель Comp сравнивать пары по первому типу в паре — и получим классический ассоциативный (мета-)контейнер! Мы ещё вернёмся к этой идее в конце статьи.Вставка
Настало время научиться строить деревья с помощью метафункций (не для того же всё затевалось, чтобы рисовать деревья руками так, как мы это сделали ранее?). Наш рекурсивный алгоритм вставки будет создавать новое дерево:
/// Вход: T - дерево, k - тип-ключ для вставки, /// выход: T' - новое дерево со вставленным элементом
INSERT(T,k):
ЕСЛИ T == NIL
ВЫВОД {NIL, k, NIL}
ИНАЧЕ
ЕСЛИ k < T.KEY
ВЫВОД {INSERT(T.LEFT,k), T.KEY, T.RIGHT}
ИНАЧЕ
ВЫВОД {T.LEFT, T.KEY, INSERT(T.RIGHT,k)}
Поясним его работу: если дерево, в которое происходит вставка, пусто, то вставляемый элемент создаст новое дерево {NIL,k,NIL}, т.е. просто лист с этим элементом (дно рекурсии). Если же дерево не пусто, то мы должны рекурсивно проваливаться до пустого дерева (т.е. до момента, пока левое или правое поддеревья не окажутся пустыми), и в итоге сформировать в этом поддереве тот же лист {NIL,k,NIL} вместо NIL, по пути «подвешивая» себя в виде нового левого или правого поддерева. В мире типов изменять существующие типы мы не можем, но можем создавать новые — это и происходит на каждом шаге рекурсии. Реализация:
template <typename Tree, typename T, typename Comp = typename Tree::comp>
struct insert;
/// Дно рекурсии
template <typename T, typename Comp>
struct insert<NIL,T,Comp> { using type = leaf<T,Comp>; };
/// Основной шаблон
template <typename Tree, typename T, typename Comp>
struct insert {
using type = typename std::conditional<
Comp::template lt<T, typename Tree::type>::value, // k < T.KEY?
node<typename Tree::type, // новое дерево {INSERT(T.LEFT,k), T.KEY, T.RIGHT}
typename insert<typename Tree::LT, T, Comp>::type,
typename Tree::RT,
Comp>,
node<typename Tree::type, // новое дерево {T.LEFT, T.KEY, INSERT(T.RIGHT,k)}
typename Tree::LT,
typename insert<typename Tree::RT, T, Comp>::type,
Comp>
>::type;
};
Для добавления элемента в пустое дерево надо явно указать компаратор
Comp; если же дерево не пусто, компаратор берётся по-умолчанию из корня этого дерева*.Сложность такой вставки: O(n) инстанцирований (n — количество уже существующих узлов), глубина рекурсии равна h (h — высота дерева). Пример явного использования:
using t2 = leaf<num_t<5>, num_comp>;
using t3 = insert_t<t2, num_t<3>>;
using t4 = insert_t<t3, num_t<7>>;
static_assert(height<t4>::value == 2, ""); // первые 2 уровня
using t5 = insert_t<insert_t<insert_t<t4, num_t<2>>, num_t<4>>, num_t<8>>;
static_assert(std::is_same<t5, t1>::value, ""); // равно первоначальному дереву
В библиотеке есть реализация метафункции
insert_tuple, позволяющая разом положить в дерево кортеж типов (под капотом это просто рекурсия insert по кортежу), пример:using t6 = insert_tuple_t<NIL, std::tuple<
num_t<5>,
num_t<7>,
num_t<3>,
num_t<4>,
num_t<2>,
num_t<8>
>, num_comp>;
static_assert(std::is_same<t1, t6>::value, "");
Обход в ширину (breadth-first traversal)
Обход в ширину бинарного дерева (или поиск в ширину из теории графов) формирует список узлов в порядке «по уровням» — сначала выводит корень, затем узлы с глубиной 1, затем с глубиной 2 и т.д. Алгоритм такого обхода использует очередь узлов для дальнейшего вывода (а не стек), поэтому он плохо поддаётся «конвертации» в рекурсивный. Под спойлером далее интересующийся читатель найдёт обходное решение. Здесь отметим лишь тот полезный факт, что «разобранное» обходом в ширину дерево может быть собрано обратно в точно такое же последовательной вставкой элементов из кортежа результата обхода. На рисунке предствлен обход в ширину нашего тестового дерева:
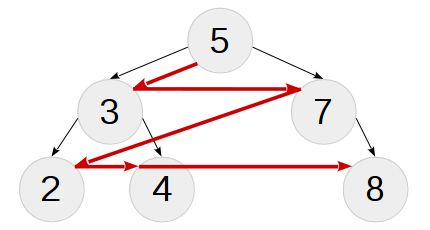
Рекурсивный обход в ширину:
Идея проста: проходимся циклом от 0 до высоты дерева h и на каждой итерации выводим только узлы с нужного уровня. Последняя операция может быть реализована рекурсивно:
Полную реализацию на шаблонах читатель может найти в репозитории. В отличие от всех рассмотренных ранее операций, обход в ширину будет иметь сложность O(nh) инстанцирований из-за наличия цикла по высоте (который, хоть и превратится в хвостовую рекурсию, будет содержать пересчёт
/// Вход: T - дерево, l - уровень для вывода, /// выход: t - список узлов этого уровня
COLLECT_LEVEL(T,l):
ЕСЛИ T == NIL
ВЫВОД {}
ИНАЧЕ
ЕСЛИ l == 0
ВЫВОД {T.KEY}
ИНАЧЕ
ВЫВОД COLLECT_LEVEL(T.LEFT,l-1) + COLLECT_LEVEL(T.RIGHT,l-1)
Полную реализацию на шаблонах читатель может найти в репозитории. В отличие от всех рассмотренных ранее операций, обход в ширину будет иметь сложность O(nh) инстанцирований из-за наличия цикла по высоте (который, хоть и превратится в хвостовую рекурсию, будет содержать пересчёт
collect_level для всего дерева на каждом шаге).Удаление?
Удаление узла — задача нетривиальная. Классический подход рассматривает 3 случая (по количеству дочерних узлов), и в алгоритме используются понятия последующего и родительского узла. Без обратной ссылки на родительский узел (см. спойлер «Об отцах и детях»), эффективно реализовать алгоритм проблематично: каждая операция подъёма вверх по дереву должна будет иметь сложность O(n). Наивная реализация такого удаления приведёт к «комбинаторному взрыву» по количеству инстанцирований (сложность что-то около O(nn)). Разработка метафункции удаления узла входит в дальнейшие планы по усовершенствованию библиотеки. См. UPD2 в конце статьи.
Применение
Переведём дух и наконец уделим внимание вопросу, зачем может понадобиться бинарное дерево поиска времени компиляции? Есть три ответа:
Неконструктивный:
*Картинка с троллейбусом*. Опустим.
Очевидный:
...для имеющих исследовательский интерес

Конструктивный:
Приведём примеры возможных применений подобной структуры:
- Сортировка типов: симметричный обход дерева формирует кортеж со списком типов, отсортированным в терминах заданного компаратора. Определение пары вспомогательных шаблонов псевдонимов позволяет одной командой «отсортировать» заданный кортеж. Как самоцель для разработки дерева — не самое полезное применение (сложность — O(n2) инстанцирований), но как лёгкий естественный бонус — вполне имеет право на существование.
- Плоская runtime структура данных: после проделанной работы не составит особого труда наделить каждый узел дерева не только статическими полями, но и данными-членами. После инстанцирования дерево превратится в подобие кортежа
std::tuple— плоскую структуру данных. Разумеется, в runtime изменять его структуру уже будет нельзя, но доступ по типу и обходы всё ещё будут полезными операциями, так как будут разворачиваться на этапе компиляции без единой строчки машинного кода (какstd::getв применении кstd::tuple).
- Ассоциативный контейнер в compile-time: в первом приближении такое дерево можно использовать как аналог
std::map(или множестваstd::set) — если вспомнить, что даже строки (точнее, строковые литералы) особой магией можно превратить в типы (и даже выполнять типичные строковые операции — конкатенацию, поиск подстрок и т.д.), такое дерево может играть ту же роль в compile-time, какую его старшие братья играют в runtime реализациях самых разных алгоритмов. Примеры: деревья суффиксов, дерево алгоритма Хаффмана, синтаксические деревья. А ещё: чувствуете этот дивный аромат рефлексии?
- Генерация иерархий: как упоминалось в примечании «Лирическое отступление», Александреску использовал шаблоны для генерации сложных иерархий наследования. Дерево само по себе уже является иерархической структурой, поэтому, думаю, оно может найти применение в аналогичных задачах.
Лирическое отступление:
Через книгу «Modern C++ Design: Generic Programming and Design Patterns Applied» (в России изданная под названием «Современное проектирование на С++», см. список литературы) известного исследователя и популяризатора шаблонного программирования Андрея Александреску красной нитью проходит мысль: «заставьте компилятор делать за вас как можно большую часть работы». Автор книги применял это стало мейнстримом он официально появился в стандарте C++11, разработал и исследовал концепцию стратегий (или политик, policy), которая сегодня применяется в существенной части STL, фактически в рамках стандарта C++98 реализовал кортежи («списки типов») и описал процесс создания с их помощью сложных иерархий наследований (меня в своё время крайне впечатлил тот факт, что на момент написания книги многие концепты, введенные Александреску и теоретически соответствовавшие стандарту, просто не компилировались большинством компиляторов того времени).
Собственно, это к слову об основной мотивации адептов метапрограммирования: перенести как можно большую часть работы в compile-time — правила мира времени компиляции гораздо строже, однако цена ошибки намного ниже (чаще всего программа всего лишь не скомпилируется, а не выстрелит в ногу после запуска), а хорошо отлаженные библиотеки шаблонов являются незаменимым подспорьем в разработке промышленного ПО (на низком уровне практически любой «велосипед», порожденный хотелками заказчика, может быть описан стандартным шаблоном с небольшим количеством предметно-ориентированных настроек).
static_assert до того, как Собственно, это к слову об основной мотивации адептов метапрограммирования: перенести как можно большую часть работы в compile-time — правила мира времени компиляции гораздо строже, однако цена ошибки намного ниже (чаще всего программа всего лишь не скомпилируется, а не выстрелит в ногу после запуска), а хорошо отлаженные библиотеки шаблонов являются незаменимым подспорьем в разработке промышленного ПО (на низком уровне практически любой «велосипед», порожденный хотелками заказчика, может быть описан стандартным шаблоном с небольшим количеством предметно-ориентированных настроек).
В довершение хочу сказать несколько слов о задаче, сподвигнувшей к разработке дерева и написанию статьи. Существует несколько алгоритмов прямой конвертации регулярного выражения в ДКА (детерминированный конечный автомат), его распознающий, часть которых оперирует т.н. синтаксическим деревом, которое по своей природе «не более чем» бинарное. Таким образом, бинарное дерево поиска времени компиляции — составная часть (и просто интересная структура для реализации) compile-time парсера регулярных выражений (после компиляции и встраивания способного развернуться в плоский код своего ДКА), который, в свою очередь, станет частью другого проекта.
Что потом?
Шёпотом: Зима...
Если настоящая статья вызовет интерес и найдёт своего читателя, я с удовольствием продолжу тему метапрограммирования (и, возможно, не только) в следующих публикациях. Из вкусного — упоминавшаяся работа со строками времени компиляции, математика времени компиляции (например, ро-факторизация Полларда),
Конструктивная критика категорически приветствуется!
std-совместимый контейнер (с итераторами — сам tutorial по разработке контейнеров должен быть интересен). Более того, на горизонте проект парсера регекспов и некоторые другие наработки нашей команды.Конструктивная критика категорически приветствуется!
Литература
- Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е. — М.: Вильямс, 2005. — 1296 с.
- Александреску А. Современное проектирование на С++: Обобщенное программирование и прикладные шаблоны проектирования = Modern C++ Design: Generic Programming and Design Patterns Applied. — С. П.: Вильямс, 2008. — 336 с. — (С++ in Depth).
- Саттер Г., Андрей Александреску. Стандарты программирования на С++. Серия «C++ In-Depth» = C++ Coding Standards: 101 Rules, Guidelines and Best Practices (C++ In-Depth). — М.: «Вильямс», 2014. — 224 с.
- Готтшлинг П. Современный C++ для программистов, инженеров и ученых. Серия «C++ In-Depth» = Discovering Modern C++: A Concise Introduction for Scientists and Engineers (C++ In-Depth). — М.: «Вильямс», 2016. — 512 с.
→ Репозиторий
UPD:
Реабилитация std::conditional:
Пользователь izvolov сделал важное замечание о правильном использовании
std::conditional. Исправленная версия search без дополнительных специализаций и сложностью O(h) инстанцирований:Обновление в репозитории (+template <typename Node, typename T, typename Comp> struct search { using type = typename std::conditional< Comp::template eq<T, typename Node::type>::value, Node, typename search<typename std::conditional< Comp::template lt<T, typename Node::type>::value, typename Node::LT, typename Node::RT >::type, T, Comp>::type >::type; };
insert) в процессе.UPD2:
Реализация remove и фикс insert и search за O(h):
Репозиторий обновлён, помимо упоминавшихся исправлений
insert и search он содержит также реализацию remove со сложностью и глубиной O(h) инстанцирований (подход похож на исправленный insert). Интересным моментом реализации является использование SFINAE+decltype для диспетчеризации и отключения веток условий на этапе компиляции (сама эта техника заслуживает отдельной небольшой статьи в виду дикой неочевидности и мощности, см. пример). Вот полная реализация remove:Комментарии в исходном коде, возможно, появятся позже. Алгоритм рекурсивного удаления, использованный в реализации, можно подсмотреть, например, здесь.template <typename Tree, typename T> struct remove { private: enum : bool { is_less = Tree::comp::template lt<T, typename Tree::type>::value }; enum : bool { is_equal = Tree::comp::template eq<T, typename Tree::type>::value }; enum : size_t { children = children_amount<Tree>::value }; using key = typename min_node_t< typename std::conditional< is_equal && children == 2, typename Tree::RT, leaf<typename Tree::type, typename Tree::comp> >::type >::type; using recursive_call = typename remove< typename std::conditional< is_less, typename Tree::LT, typename std::conditional< !is_equal || children == 2, typename Tree::RT, NIL >::type >::type, typename std::conditional< is_equal, key, T >::type >::type; static typename Tree::RT root_dispatcher(...); template <typename Bush> static typename std::enable_if< sizeof(typename Bush::LT::type), typename Bush::LT >::type root_dispatcher(Bush&&); public: using type = typename std::conditional< is_equal && (children < 2), decltype(root_dispatcher(std::declval<Tree>())), node< key, typename std::conditional< is_less, recursive_call, typename Tree::LT >::type, typename std::conditional< !is_less, recursive_call, typename Tree::RT >::type, typename Tree::comp > >::type; };