Визуализация данных — это всегда некоторое графическое построение, которое помогает исследовать имеющиеся данные. Мы строим геометрическую модель и изменяем её, чтобы представить разные аспекты данных. Также мы сталкиваемся с ограничением, которые накладывает визуальное восприятие, заключающемся в том, что размерность визуализации не может быть больше двух. Все доступные графические средства двумерны: лист бумаги или экран монитора.
На примере диаграмм для одномерных данных посмотрим, как строится геометрическая модель, как она модифицируется, и как проявляется размерность данных и визуализации.
Простейшая геометрическая модель числовых значений
Рассмотрим ряд значений одной переменной (скорость, температура, цена и т.п.), например:
3, 1, 5, 4, 6, 5, 4, 7, 9, 8
Под одномерностью данных и будем понимать, что переменная только одна. Чтобы исследовать свойства числового ряда, построим геометрическую модель, то есть модель, где элементы данных (числовые значения) представлены с помощью геометрических объектов: точек, линий и окружностей.
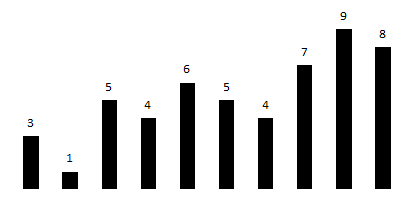
Для числового ряда самое простое — это сопоставить каждому числу линию, длина которой пропорциональны числовым значениям. Например, линия, соответствующая числу 3, в три раза длиннее линии, соответствующей числу 1. Получается обычная столбиковая диаграмма:
Преобразование визуализации для исследования разных аспектов данных
Теперь будем изменять простейшую модель числового ряда, чтобы исследовать разные его аспекты.
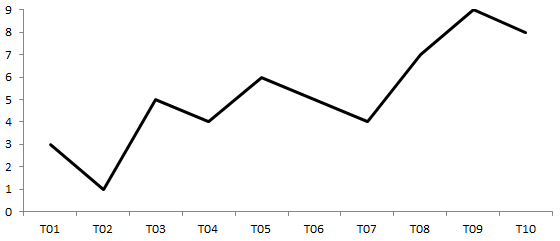
Значимым параметром у столбиковой диаграммы является расстояние от основания диаграммы (горизонтальной оси) до верхней точки. Это расстояние пропорционально значению переменной в некоторый момент времени. Если оставить только верхние точки и соединить их между собой, то получится график (line chart). На графике точки упорядочены по времени слева направо:
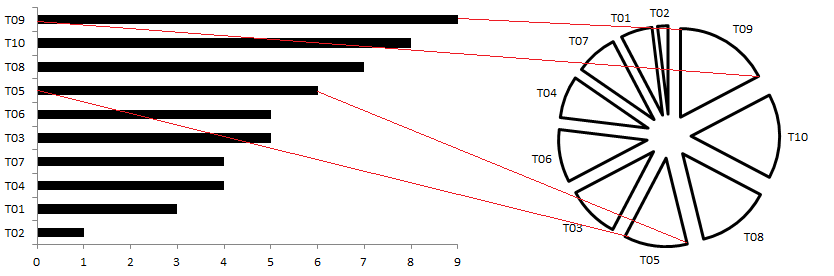
Если отсортировать линии не по времени, а по возрастанию или убыванию, то получится линейчатая диаграмма (bar chart). Эта диаграмма хорошо подходит для представления рейтинга и позволяет визуализировать значения переменной, упорядоченные по убыванию или возрастанию сверху вниз (по рангу). Тогда она будет похожа на упорядоченный список:

Теперь преобразование посложнее. Отсортированный набор линий мы разбиваем на группы. В каждой группе есть только линии определенной длины, не больше и не меньше заданных граничных значений. Для каждой группы мы считаем количество линий (значений) попадающих в заданный интервал. Полученному значению ставим в соответствие новую линию. Как будто исходные линии стали плашками, и мы их укладываем одну на другую. Дальше новые линии расставляем в порядке возрастания максимальной (минимальной) границы интервала и получается гистограмма.
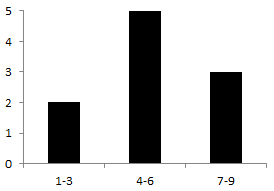
У гистограммы по горизонтальной оси указаны значения исходной переменной, в отличие от линейчатой диаграммы. Поэтому линейчатую диаграмму лучше делать горизонтальной — чтобы не путать с гистограммой, особенно если они используются одновременно.
Уменьшение размерности визуальной модели
Можно заметить, что рассмотренные выше диаграммы двумерны, несмотря на то, что при их помощи визуализируются одномерные данные:
- график: время и значение переменной
- линейчатая диаграмма: значение переменной и ранг (для горизонтальной ориентации линий)
- гистограмма: интервал и количество значений
То есть, размерность визуализации не обязательно совпадает с размерностью данных.
Эффективно увеличивать размерность визуализации сложно, а вот уменьшить размерность можно достаточно легко. Такая модификация позволит получить еще несколько диаграмм для визуализации и моделирования значений одной переменной.
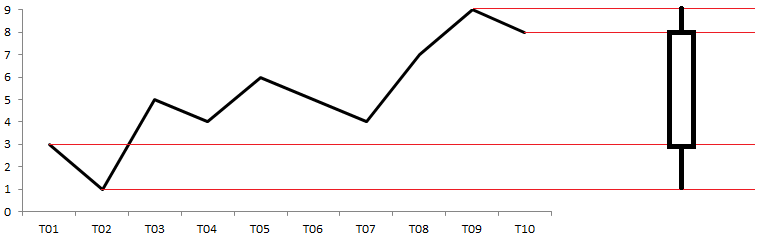
Одномерным аналогом графика является интервальная диаграмма или японская свеча (candlestick chart), часто используемая при отображении биржевых графиков. Для ее построения мы оставляем только четыре значения переменной: начальное, конечное, минимальное и максимальное. Вместо того, чтобы изучать временной интервал в подробностях, мы смотрим только на граничные (по времени и величине) значения. У интервальной диаграммы прямоугольник не закрашен, если конечное значение больше начального (рост), и закрашен, если наоборот (падение).
Теперь возьмем все линии, образующие линейчатую диаграмму, и соединим их последовательно. Берем самую длинную линию, соответствующую максимальному значению, к ней приставляем следующую по величине и т.д. А потом замкнем начальную и конечную точку так, чтобы получилась окружность. Таким образом, каждая линия, соответствующая переменной, становится дугой окружности, а сама окружность соответствует целому — сумме всех значений. При этом доле каждого значения соответствует сектор окружности и некоторый угол, пропорциональный доле.
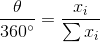
Мы получили круговую диаграмму (pie chart).
И, наконец, уменьшим размерность гистограммы. По аналогии с интервальным графиком оставим лишь несколько основных значений, характеризующих распределение: минимальное и максимальное, два квартиля и медиану. Получим диаграмму размаха или ящик с усами (box plot), на которой квартили задают границы прямоугольника, а вертикальная линия по середине, это медиана.
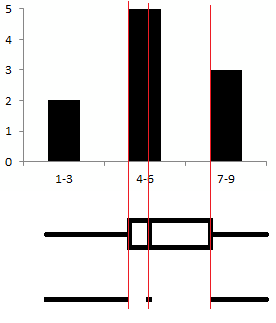
Нижний вариант, предложенный "минималистом" Тафти, наглядно демонстрирует одномерность данной визуализации.
Интервальный график (японская свеча) и диаграмма размаха (ящик с усами) очень похожи. Поэтому, особенно если они используются вместе, лучше свечу ориентировать вертикально, а ящик горизонтально.
В целом, представление с меньшей размерностей, как бы сжатое, позволит строить визуализации, на которых сравниваются несколько рядов значений.
Выбор диаграммы для визуализации одномерных данных
Теперь составим таблицу, которая поможет выбирать диаграммы для визуализации одномерных данных. Шесть рассмотренных диаграмм классифицированы по следующим аспектам визуализации:
- Временная последовательность (подробно или кратко)
- Отношение: между значениями и значений к целому
- Распределение значений по интервалам (подробно и кратко)
| Размерность | Время | Отношение | Распределение |
|---|---|---|---|
| 2D | График | Линейчатая диаграмма | Гистограмма |
| 1D | Интервальный график («японская свеча») | Круговая диаграмма | Диаграмма размаха («ящик с усами») |
Выводы
- Диаграммы для одномерных данных представлены как геометрическая модель и рассмотрены связи между различными диаграммами
- Модификации геометрической модели (визуализации) позволяют показать разные аспекты изучаемых данных
- Изменение размерности диаграмм позволяет представить информацию в более сжатом виде, например, для сравнения
Ссылки
- Диаграммы и графики: осмысляя Тафти
- Как убежать от плоскости: рецензия на книгу "Представление информации" Эдварда Тафти
- The Data Visualisation Catalogue
- Интервальный график ("японские свечи")
- Пример упрощения интервального графика
- Диаграмма размаха ("ящик с усами")
- Гистограмма и ящик с усами на пальцах
- Говори на языке диаграмм