Звездное небо напоминает, — точки являются фундаментальной абстракцией, основой окружающего пространства.
Это первая статья серии, посвященной описанию свойств базисов пространств на основе элементов (а не векторов). Базис определяет систему координат — описание элементов пространства в виде набора чисел, характеризующих положение элемента относительно базиса.
Если пространство является метрическим, то базис задает метрические тензоры, позволяющие определять расстояния между элементами пространства по их координатам.
Метрика базиса может быть задана либо через значения скалярных произведений, либо через значения связей между элементами базиса. Поэтому базис может быть определен как в обычном геометрическом пространстве, так и в дуальном — пространстве графа. В геометрическом пространстве элементами базиса будут вершины симплекса. В графе — узлы графа.
В первой статье продемонстрируем взаимность симплекса и графа. Определим взаимные метрические тензоры — грамиан и лапласиан базиса. Свяжем их с параметрами графов и симплексов. Покажем роль нормали пространства.
Во второй определим систему координат на основе точечного базиса. Два типа взаимных координат характеризуют объект — би- и ди-координаты. В полном базисе координаты позволяют определять расстояния между элементами вне базисного пространства.
В третьей статье разбираемся с полезным понятием — скалярным произведением упорядоченных пар, которое является обобщением нормы вектора, — квадрата расстояния между элементами пространства.
Далее обращаемся к пространству графа. Решаем задачу Дирихле. Показываем, как понятие фундаментальной матрицы связано с определением расстояний между элементами вне пространства подграфа.
В 5-й части рассмотрим преобразование координат при изменении базиса. Преобразования точечных базисов используются, например, в задачах локализации сенсоров (определения их координат).
Наконец, в заключение рассмотрим базис простейшей структуры — граф-звезда. Используем его для описания пространства положительных целых чисел, которые раскладываются на произведение простых.
Поехали!
Пусть у нас есть множество, состоящее из n элементов. Элементами могут быть геометрическая точка в пространстве, узел графа, буква, слово, документ, человек и прочее, — практически любой объект. Допустим, что известна степень близости элементов набора. Для точек в пространстве степенью близости является квадрат расстояния между ними. В физике мера близости между двумя событиями именуется интервалом.
Иногда вместо квадрата расстояния используют термин «квадранс», но поскольку он редко употребляем, то мы чаще будем употреблять более благозвучный термин «дистанция». Квадрат расстояния между элементами
и 
будем обозначать как: 
. Если речь идет о дистанциях между элементами множества, то скаляр превращается в матрицу: 
, строчные индексы обозначают множество. Кортеж дистанций от заданного элемента множества до остальных состоит из набора скалярных дистанций:
![$q_{Pa}=[q_{PA}, q_{PB},...] \quad(1.1)$](https://habrastorage.org/getpro/habr/formulas/5d1/b72/94c/5d1b7294ce2e2a19f7fd462e86c96e6e.svg)
Набор независимых точек с известными дистанциями между ними задает симплекс. В двумерном пространстве симплекс определяется 3-мя вершинами (треугольник), в трехмерном — 4-мя (тетраэдр) и т.д., — мерность симплекса на 1 меньше количества его вершин. Вершины являются независимыми, если объем симплекса отличен от нуля.
Дистанции между вершинами симплекса задают дистанционную матрицу
. На рисунке показан прямоугольный треугольник (2-мерный симплекс) с катетами 3, 4 и гипотенузой 5. Его матрица дистанций имеет вид:
Для электрической цепи сопротивлений дистанция равна эффективному сопротивлению между узлами сети. А поскольку любая электросеть — это граф, то матрицу дистанций в теории графов называют матрицей резистивных расстояний (resistance distance matrix). Итак, понятие дистанции универсально — может использоваться как для привычного геометрического пространства, так и для пространства графа. Это означает также, что каждому невырожденному симплексу соответствует некий граф и наоборот.
На вершинах симплекса (или графа) можно определить базис пространства. Но для задания метрики нужно определить метрический тензор. Дистанционная матрица не подходит для роли метрического тензора хотя бы потому, что ее определитель не связан с объемом симплекса (в примере — с площадью треугольника).
Однако еще в 19-м веке A.Cayley (Кэли) обнаружил, что если окаймить дистанционную матрицу кортежем из единиц, то определитель полученной матрицы будет пропорционален квадрату объема симплекса. Окаймленную единицами матрицу дистанций называют матрицей Кэли-Менгера.
Определим операцию окаймления
симметричных матриц 
кортежем 
и скаляром 
:
Если матрица
является окаймлением матрицы , то является подматрицей и называется главным (угловым) минором .
Математики (J.C.Gower) также заметили, что удобнее оперировать не с самими дистанциями между элементами, а с отрицательными полудистанциями
.
Это объясняется тем, что отрицательные полудистанции отражают скалярное произведение элементов, как следует из раскрытия формулы для квадрата расстояния (дистанции) между элементами:
Отсюда получаем связь матрицы дистанций и матрицы скалярных произведений 
:
Здесь
— нормы элементов, диагональ матрицы скалярных произведений. В тензорной форме:
Не менее важна обратная формула — позволяет получать дистанционную матрицу на основе грамианов:
К множеству обычных элементов пространства добавим необычный. А именно — вектор нормали пространствa
. Пространством нормали является ортогональное дополнение к пространству элементов. Скалярное произведение нормали с элементами обычного пространства равно единице, а с самим собой — ноль.
Нормаль ортогональна всем векторам пространства, поэтому ее называют также аннулятором. Набор из элементов, содержащий нормаль пространства, будем называть мажорным (полным), чтобы отличать его от набора в котором нормали нет. Нормаль будем ставить в наборе на первое место.
Теперь мы готовы к определению метрического тензора. Дистанционный метрический тензор
является набором скалярных произведений между элементами мажорного множества:
Матрицы скалярных произведений (векторов) называют матрицами Грама. Тот же термин будем использовать и для скалярных произведений элементов, в сокращенной форме — грамиан. Таким образом дистанционный метрический тензор является грамианом мажорного базиса.
Для нашего симплекса из трех вершин (прямоугольный треугольник) дистанционный метрический тензор будет иметь вид:
Отметим, что размерность дистанционного тензора на два больше размерности обычного векторного тензора при описании пространства одной и той же мерности. То есть данный тензор содержит больше информации.
Для грамианов будем использовать нижние индексы:
Определитель метрического тензора связан с объемом симплекса 
. Точная формула:
где
— мерность пространства, задаваемого симплексом из 
вершин.
Вычислим площадь нашего треугольника. Имеем
. Тогда 
, откуда 
. Конечно, данную площадь можно было получить и просто перемножением длин катетов 
.
Другая полезная характеристика, содержащаяся в ДМТ, — это значение нормы ортогонального центра базиса. В терминах геометрии данная норма равна квадрату радиуса описанной сферы вокруг вершин симплекса. То есть ортогональный центр можно интерпретировать как
-мерную сферу. Ортогональный центр задает важные характеристики базиса, будем обозначать его как 
. Ортоцентр — это элемент пространства с нормой 
. Данную норму можно найти как отношение определителей углового минорного и мажорного грамианов базиса:
В нашем треугольнике норма базиса будет равна:
.
Для метрического тензора всегда существует обратный, который называется также взаимным. Обращение дистанционного метрического тензора назовем лапласовским метрическим тензором
— ЛМТ. Связь тензоров:
, где 
— единичная матрица.
Почему обратный дистанционный метрический тензор стал лапласовским? Потому что его главным угловым минором (подматрицей) является лапласиан
. Та самая матрица, которой описывают узлы и связи в графе, ее называют также матрицей Кирхгофа. Можно сказать, что формула (1.8) связывает свойства симплексов и графов. Каждому лапласиану соответствует грамиан и наоборот. Такая взаимность позволяет сопоставлять геометрические характеристики симплексов с параметрами графов.
Лапласовский метрический тензор обозначаем верхними индексами:
.
Лапласовский метрический тензор — это мажорный лапласиан, окаймление обычного (минорного) лапласиана. Окаймление отражает параметры ортоцентра базиса (1.7):
Скаляр — это норма ортоцентра (в терминах графа — обратная геометрическая связность), 
— барицентрические координаты ортоцентра. Барицентрические координаты — это весовые координаты элемента относительно базовых (реперов) — вершин симплекса или графа. Сумма весов равна единице — условие нормировки барицентрических компонент.
Раскрывая умножение метрических тензоров (1.8) по правилам произведения блочных матриц,
получаем 4-м основных тождества.
Сумма компонент барицентрических координат ортоцентра равна 1:
Сумма значений строк (и столбцов) лапласиана равна 0. Это означает, что строки лапласиана представляют собой барицентрические координаты неких векторов:
:
Свойство равноудаленности базовых вершин (симплекса или графа) от ортоцентра:
Наконец, связь минорных грамиана и лапласиана:
Матрицы вида
, где 
— некий барицентрический вектор, называют матрицами трансляции. Они могут быть использованы, например, для переноса начала координат некого набора данных 
в точку, определяемую барицентрическими координатами . Данные матрицы являются проекторами.
Сопоставим геометрические параметры симплекса с характеристиками лапласиана.
Матричная теорема о деревьях связывает количество остовных деревьев графа с определителем минора лапласиана. В предыдущих статьях данная величина именовалась скалярным потенциалом лапласиана
:
Здесь через
обозначен псевдодетерминант, то есть детерминант от минора лапласиана (поскольку сам лапласиан — вырожденная матрица). — мерность пространства, на единицу меньше количества элементов базиса.
Видим, что чем меньше количество остовных деревьев графа (проще его структура), тем больше объем соответствующего ему симплекса.
Лапласиан можно рассматривать и как характеристику симплекса, и как параметры связей узлов графа. В терминах графов значениями лапласиана является величина связи между узлами (с обратным знаком), а на диагонали расположена общая сумма связей узлов.
Вид лапласиана для нашего примера:
Здесь проводимость (вес связи) между узлами A и B равна 16/144, между узлами A и C 9/144, а между узлами B и C связи вообще нет.
Теперь выясним геометрический смысл элементов лапласиана. Каждой вершине симплекса можно сопоставить соответствующую противоположную грань. Под противоположной понимается грань симплекса, которая не касается заданного узла. Очевидно, что в общем случае такая грань является многомерной. В нашем треугольнике — это сторона (отрезок), противоположная вершине. В тетраэдре — треугольник. Опуская из заданной вершины перпендикуляр на противоположную грань, получаем высоту вершины симплекса. Произведение высоты вершины
на площадь противоположной грани 
дает объем симплекса , умноженного на мерность его пространства :
Элементы лапласиана симплекса можно выразить через высоты вершин. Диагональные элементы лапласиана обратно пропорциональны высотам:
Высота вершины — это дистанция до подпространства оставшихся вершин базиса. То есть чем
больше высоты вершин симплекса — тем менее компактен симплекс. В терминах графа — чем больше проводимость (связность) вершин — тем компактнее граф.
Недиагональные элементы пропорциональны косинусу угла между гранями симплекса
:
Прямой угол между гранями симплекса эквивалентен отсутствию связи между соответствующими узлами в графе.
Из соотношений (1.12), (1.13) и (1.14.1) можно получить геометрический смысл отношения следа лапласиана
к его скалярному потенциалу . Эта величина связана с суммой квадратов площадей граней симплекса:
Здесь
— мерность грани.
Величина, обратная норме ортоцентра базиса, с геометрической точки зрения равна кривизне. А в пространстве графа данная норма характеризует его связность. Назовем данную связность геометрической и обозначим как 
:
Размерность геометрической связности совпадает с размерностью величины связи между узлами. Так, если для электрических сетей проводимость между узлами измеряется в сименсах, то и геометрическая связность будет в сименсах.
Если норма ортоцентра базиса характеризует связность графа, то его барицентрические координаты можно интерпретировать как вклады в связность, — значения компонент показывают, насколько узел связан с графом. Чем менее связан с остальным графом — тем больше значение данной компоненты ортоцентра. Узлы сочленения имеют, как правило, отрицательные значения компонент связности. Поэтому барицентрические координаты ортоцентра
удобно называть вектором связности.
Рассчитаем параметры популярного в Википедии графа.
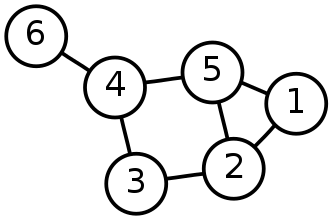
Данный граф эквивалентен 6-вершинному симплексу в 5-мерном пространстве. Кружки с цифрами — это пронумерованные узлы графа. Силу связи между узлами (значение веса ребер) принимаем за единицу.
Геометрическая связность данного графа равна 1.663 — это средняя связность на один узел. Можно сравнить ее с максимальной (7.2) и минимальной (0.8) связностью для графа из 6 узлов. Индекс симметричности — 0.773.
Вектор связности узлов (барицентрические координаты ортоцентра): [0.364, 0.045, 0.273, -0.227, 0.045, 0.500]. Видим, что чем больше узел имеет связей, тем меньше значение его связности и наоборот. Отметим отрицательное значение связности 4-го узла. Это единственной узел графа, при удалении которого граф распадается на две несвязанные компоненты. Возможно, что компоненты с отрицательной связностью являются ключевыми узлами графа.
___
Подводим итоги. Определены взаимные метрические тензоры на элементах пространства, грамиан и лапласиан мажорного базиса. Показана связь симплексов и графов. В следующей статье покажем, как задавать координаты элементов в базисе.
Оглавление
Введение
Это первая статья серии, посвященной описанию свойств базисов пространств на основе элементов (а не векторов). Базис определяет систему координат — описание элементов пространства в виде набора чисел, характеризующих положение элемента относительно базиса.
Если пространство является метрическим, то базис задает метрические тензоры, позволяющие определять расстояния между элементами пространства по их координатам.
Метрика базиса может быть задана либо через значения скалярных произведений, либо через значения связей между элементами базиса. Поэтому базис может быть определен как в обычном геометрическом пространстве, так и в дуальном — пространстве графа. В геометрическом пространстве элементами базиса будут вершины симплекса. В графе — узлы графа.
План и содержание серии
В первой статье продемонстрируем взаимность симплекса и графа. Определим взаимные метрические тензоры — грамиан и лапласиан базиса. Свяжем их с параметрами графов и симплексов. Покажем роль нормали пространства.
Во второй определим систему координат на основе точечного базиса. Два типа взаимных координат характеризуют объект — би- и ди-координаты. В полном базисе координаты позволяют определять расстояния между элементами вне базисного пространства.
В третьей статье разбираемся с полезным понятием — скалярным произведением упорядоченных пар, которое является обобщением нормы вектора, — квадрата расстояния между элементами пространства.
Далее обращаемся к пространству графа. Решаем задачу Дирихле. Показываем, как понятие фундаментальной матрицы связано с определением расстояний между элементами вне пространства подграфа.
В 5-й части рассмотрим преобразование координат при изменении базиса. Преобразования точечных базисов используются, например, в задачах локализации сенсоров (определения их координат).
Наконец, в заключение рассмотрим базис простейшей структуры — граф-звезда. Используем его для описания пространства положительных целых чисел, которые раскладываются на произведение простых.
Поехали!
Дистанционная матрица
Пусть у нас есть множество, состоящее из n элементов. Элементами могут быть геометрическая точка в пространстве, узел графа, буква, слово, документ, человек и прочее, — практически любой объект. Допустим, что известна степень близости элементов набора. Для точек в пространстве степенью близости является квадрат расстояния между ними. В физике мера близости между двумя событиями именуется интервалом.
Иногда вместо квадрата расстояния используют термин «квадранс», но поскольку он редко употребляем, то мы чаще будем употреблять более благозвучный термин «дистанция». Квадрат расстояния между элементами
и будем обозначать как: . Если речь идет о дистанциях между элементами множества, то скаляр превращается в матрицу: , строчные индексы обозначают множество. Кортеж дистанций от заданного элемента множества до остальных состоит из набора скалярных дистанций:Набор независимых точек с известными дистанциями между ними задает симплекс. В двумерном пространстве симплекс определяется 3-мя вершинами (треугольник), в трехмерном — 4-мя (тетраэдр) и т.д., — мерность симплекса на 1 меньше количества его вершин. Вершины являются независимыми, если объем симплекса отличен от нуля.
Дистанции между вершинами симплекса задают дистанционную матрицу
. На рисунке показан прямоугольный треугольник (2-мерный симплекс) с катетами 3, 4 и гипотенузой 5. Его матрица дистанций имеет вид:Для электрической цепи сопротивлений дистанция равна эффективному сопротивлению между узлами сети. А поскольку любая электросеть — это граф, то матрицу дистанций в теории графов называют матрицей резистивных расстояний (resistance distance matrix). Итак, понятие дистанции универсально — может использоваться как для привычного геометрического пространства, так и для пространства графа. Это означает также, что каждому невырожденному симплексу соответствует некий граф и наоборот.
Окаймление матриц
На вершинах симплекса (или графа) можно определить базис пространства. Но для задания метрики нужно определить метрический тензор. Дистанционная матрица не подходит для роли метрического тензора хотя бы потому, что ее определитель не связан с объемом симплекса (в примере — с площадью треугольника).
Однако еще в 19-м веке A.Cayley (Кэли) обнаружил, что если окаймить дистанционную матрицу кортежем из единиц, то определитель полученной матрицы будет пропорционален квадрату объема симплекса. Окаймленную единицами матрицу дистанций называют матрицей Кэли-Менгера.
Определим операцию окаймления
симметричных матриц кортежем и скаляром :Если матрица
является окаймлением матрицы , то является подматрицей и называется главным (угловым) минором .Об использовании индексов
Верхнее и/или нижнее положение индексов рядом с тензором определяет тип тензора. Если тензоры 1-го ранга различаются только положением индексов (
и 
, например), то они образуют взаимную пару.
Согласно правилам произведения тензоров скалярное произведение (свертка, результат — скаляр) — это два одинаковых индекса на разной высоте (
), точечное произведение (результат — кортеж) — одинаковые индексы на одной высоте (
или 
), внешнее произведение (результат — матрица, диада) — два разных индекса (
или 
).
Заглавная буква в индексе измерения означает, что речь идет о фиксированном значении в данном измерении — элементе (
— значение кортежа 
элемента ).
Там, где природа объекта ясна из контекста, индексы в обозначении будем опускать.
и , например), то они образуют взаимную пару. Согласно правилам произведения тензоров скалярное произведение (свертка, результат — скаляр) — это два одинаковых индекса на разной высоте (
), точечное произведение (результат — кортеж) — одинаковые индексы на одной высоте ( или ), внешнее произведение (результат — матрица, диада) — два разных индекса ( или ).Заглавная буква в индексе измерения означает, что речь идет о фиксированном значении в данном измерении — элементе (
— значение кортежа элемента ).Там, где природа объекта ясна из контекста, индексы в обозначении будем опускать.
Дистанционный метрический тензор (ДМТ) — грамиан базиса
Математики (J.C.Gower) также заметили, что удобнее оперировать не с самими дистанциями между элементами, а с отрицательными полудистанциями
.Это объясняется тем, что отрицательные полудистанции отражают скалярное произведение элементов, как следует из раскрытия формулы для квадрата расстояния (дистанции) между элементами:
Отсюда получаем связь матрицы дистанций
и матрицы скалярных произведений :Здесь
— нормы элементов, диагональ матрицы скалярных произведений. В тензорной форме:Не менее важна обратная формула — позволяет получать дистанционную матрицу на основе грамианов:
К множеству обычных элементов пространства добавим необычный. А именно — вектор нормали пространствa
. Пространством нормали является ортогональное дополнение к пространству элементов. Скалярное произведение нормали с элементами обычного пространства равно единице, а с самим собой — ноль. Нормаль ортогональна всем векторам пространства, поэтому ее называют также аннулятором. Набор из элементов, содержащий нормаль пространства, будем называть мажорным (полным), чтобы отличать его от набора в котором нормали нет. Нормаль будем ставить в наборе на первое место.
Теперь мы готовы к определению метрического тензора. Дистанционный метрический тензор
является набором скалярных произведений между элементами мажорного множества:Матрицы скалярных произведений (векторов) называют матрицами Грама. Тот же термин будем использовать и для скалярных произведений элементов, в сокращенной форме — грамиан. Таким образом дистанционный метрический тензор является грамианом мажорного базиса.
Для нашего симплекса из трех вершин (прямоугольный треугольник) дистанционный метрический тензор будет иметь вид:
Отметим, что размерность дистанционного тензора на два больше размерности обычного векторного тензора при описании пространства одной и той же мерности. То есть данный тензор содержит больше информации.
Для грамианов будем использовать нижние индексы:
Геометрические свойства ДМТ
Определитель метрического тензора
связан с объемом симплекса . Точная формула:где
— мерность пространства, задаваемого симплексом из вершин.Вычислим площадь нашего треугольника. Имеем
. Тогда , откуда . Конечно, данную площадь можно было получить и просто перемножением длин катетов .Другая полезная характеристика, содержащаяся в ДМТ, — это значение нормы ортогонального центра базиса. В терминах геометрии данная норма равна квадрату радиуса описанной сферы вокруг вершин симплекса. То есть ортогональный центр можно интерпретировать как
-мерную сферу. Ортогональный центр задает важные характеристики базиса, будем обозначать его как . Ортоцентр — это элемент пространства с нормой . Данную норму можно найти как отношение определителей углового минорного и мажорного грамианов базиса:В нашем треугольнике норма базиса будет равна:
.Лапласовский метрический тензор (ЛМТ) — лапласиан базиса
Для метрического тензора всегда существует обратный, который называется также взаимным. Обращение дистанционного метрического тензора назовем лапласовским метрическим тензором
— ЛМТ. Связь тензоров:, где — единичная матрица.Почему обратный дистанционный метрический тензор стал лапласовским? Потому что его главным угловым минором (подматрицей) является лапласиан
. Та самая матрица, которой описывают узлы и связи в графе, ее называют также матрицей Кирхгофа. Можно сказать, что формула (1.8) связывает свойства симплексов и графов. Каждому лапласиану соответствует грамиан и наоборот. Такая взаимность позволяет сопоставлять геометрические характеристики симплексов с параметрами графов.Лапласовский метрический тензор обозначаем верхними индексами:
. Структура ЛМТ
Лапласовский метрический тензор — это мажорный лапласиан, окаймление обычного (минорного) лапласиана. Окаймление отражает параметры ортоцентра базиса (1.7):
Скаляр
— это норма ортоцентра (в терминах графа — обратная геометрическая связность), — барицентрические координаты ортоцентра. Барицентрические координаты — это весовые координаты элемента относительно базовых (реперов) — вершин симплекса или графа. Сумма весов равна единице — условие нормировки барицентрических компонент.Барицентрические координаты ортоцентра произвольного прямоугольного треугольника всегда одинаковы
И равны ![$\mathbf{s}=[s_A, s_B, s_C]=[0, 1/2, 1/2]$](https://habrastorage.org/getpro/habr/formulas/94e/0f2/3a5/94e0f23a522e28d31307dcf208e6134f.svg)
.
Это означает, что центр O уравновешивается равными массами элементов B и C.
Вообще говоря для любого графа, представляющего собой цепочку последовательно соединенных звеньев, координаты ортоцентра будут отличны от нуля только на крайних узлах и равны 1/2.
.Это означает, что центр O уравновешивается равными массами элементов B и C.
Вообще говоря для любого графа, представляющего собой цепочку последовательно соединенных звеньев, координаты ортоцентра будут отличны от нуля только на крайних узлах и равны 1/2.
Минорные тождества
Раскрывая умножение метрических тензоров (1.8) по правилам произведения блочных матриц,
получаем 4-м основных тождества.
Сумма компонент барицентрических координат ортоцентра равна 1:
Сумма значений строк (и столбцов) лапласиана равна 0. Это означает, что строки лапласиана представляют собой барицентрические координаты неких векторов:
: Свойство равноудаленности базовых вершин (симплекса или графа) от ортоцентра:
Наконец, связь минорных грамиана и лапласиана:
Матрицы вида
, где — некий барицентрический вектор, называют матрицами трансляции. Они могут быть использованы, например, для переноса начала координат некого набора данных в точку, определяемую барицентрическими координатами . Данные матрицы являются проекторами.Построение дистанционной матрицы по лапласиану
Если имеем дело с графом, то для построения дистанционной матрицы на основании матрицы смежности 
можно использовать следующий алгоритм. Для матрицы смежности строим лапласиан:
Здесь
— преобразование кортежа в диагональную матрицу.
Определитель лапласиана равен нулю, поэтому его нельзя просто обратить. Надо либо удалить из него какой-то узел, либо дополнить (окаймить) каким-либо вектором.
Окаймляем лапласиан вектором из единиц и обращаем полученную матрицу. Главным минором (подматрицей) результата обращения будет матрица Грина
.
— количество вершин базиса.
Матрица Грина является грамианом — матрицей скалярных произведений векторов, направленных из центра координат (здесь это центроид базиса) к элементам. Для получения дистанционной матрицы из грамиана следует использовать формулу (1.3.1).
Пусть
, где — центр. Тогда формула (1.3.1) принимает следующий вид:
можно использовать следующий алгоритм. Для матрицы смежности строим лапласиан:Здесь
— преобразование кортежа в диагональную матрицу.Определитель лапласиана равен нулю, поэтому его нельзя просто обратить. Надо либо удалить из него какой-то узел, либо дополнить (окаймить) каким-либо вектором.
Окаймляем лапласиан вектором из единиц и обращаем полученную матрицу. Главным минором (подматрицей) результата обращения будет матрица Грина
. — количество вершин базиса.Матрица Грина является грамианом — матрицей скалярных произведений векторов, направленных из центра координат (здесь это центроид базиса) к элементам. Для получения дистанционной матрицы из грамиана следует использовать формулу (1.3.1).
Пусть
, где — центр. Тогда формула (1.3.1) принимает следующий вид:Геометрия лапласиана
Сопоставим геометрические параметры симплекса с характеристиками лапласиана.
Объем симплекса и потенциал лапласиана
Матричная теорема о деревьях связывает количество остовных деревьев графа с определителем минора лапласиана. В предыдущих статьях данная величина именовалась скалярным потенциалом лапласиана
:Здесь через
обозначен псевдодетерминант, то есть детерминант от минора лапласиана (поскольку сам лапласиан — вырожденная матрица). — мерность пространства, на единицу меньше количества элементов базиса.Видим, что чем меньше количество остовных деревьев графа (проще его структура), тем больше объем соответствующего ему симплекса.
Элементы лапласиана
Лапласиан можно рассматривать и как характеристику симплекса, и как параметры связей узлов графа. В терминах графов значениями лапласиана является величина связи между узлами (с обратным знаком), а на диагонали расположена общая сумма связей узлов.
Вид лапласиана для нашего примера:
Здесь проводимость (вес связи) между узлами A и B равна 16/144, между узлами A и C 9/144, а между узлами B и C связи вообще нет.
Теперь выясним геометрический смысл элементов лапласиана. Каждой вершине симплекса можно сопоставить соответствующую противоположную грань. Под противоположной понимается грань симплекса, которая не касается заданного узла. Очевидно, что в общем случае такая грань является многомерной. В нашем треугольнике — это сторона (отрезок), противоположная вершине. В тетраэдре — треугольник. Опуская из заданной вершины перпендикуляр на противоположную грань, получаем высоту вершины симплекса. Произведение высоты вершины
на площадь противоположной грани дает объем симплекса , умноженного на мерность его пространства :Элементы лапласиана симплекса можно выразить через высоты вершин. Диагональные элементы лапласиана обратно пропорциональны высотам:
Высота вершины — это дистанция до подпространства оставшихся вершин базиса. То есть чем
больше высоты вершин симплекса — тем менее компактен симплекс. В терминах графа — чем больше проводимость (связность) вершин — тем компактнее граф.
Недиагональные элементы пропорциональны косинусу угла между гранями симплекса
:Прямой угол между гранями симплекса эквивалентен отсутствию связи между соответствующими узлами в графе.
Из соотношений (1.12), (1.13) и (1.14.1) можно получить геометрический смысл отношения следа лапласиана
к его скалярному потенциалу . Эта величина связана с суммой квадратов площадей граней симплекса:Здесь
— мерность грани.Ортоцентр и связность графа
Величина, обратная норме ортоцентра базиса
, с геометрической точки зрения равна кривизне. А в пространстве графа данная норма характеризует его связность. Назовем данную связность геометрической и обозначим как :Размерность геометрической связности совпадает с размерностью величины связи между узлами. Так, если для электрических сетей проводимость между узлами измеряется в сименсах, то и геометрическая связность будет в сименсах.
Значения геометрической связности в различных топологиях графа
Для полного графа (все узлы связаны со всеми) с одной и той же силой связи выражение для связности в зависимости от количества узлов имеет следующий вид:
В больших графах значение связности совпадает с количеством связей узла, что и ожидается от подобного инварианта.
Формула (1.16.1) выражает максимальное значение связности для заданного количества узлов. Минимальной является связность деревьев — графов без циклов с одной компонентой связности. К деревьям относятся, например, разомкнутая цепочка и звезда. Выражение для минимальной связности имеет вид:
Для сравнения приведем также связность замкнутой цепи — промежуточное значение между максимальной и минимальной связностью:
В обоих случаях связность падает линейно с ростом размера графа.
выражение для связности в зависимости от количества узлов имеет следующий вид:В больших графах значение связности совпадает с количеством связей узла, что и ожидается от подобного инварианта.
Формула (1.16.1) выражает максимальное значение связности для заданного количества узлов. Минимальной является связность деревьев — графов без циклов с одной компонентой связности. К деревьям относятся, например, разомкнутая цепочка и звезда. Выражение для минимальной связности имеет вид:
Для сравнения приведем также связность замкнутой цепи — промежуточное значение между максимальной и минимальной связностью:
В обоих случаях связность падает линейно с ростом размера графа.
Если норма ортоцентра базиса характеризует связность графа, то его барицентрические координаты можно интерпретировать как вклады в связность, — значения компонент показывают, насколько узел связан с графом. Чем менее связан с остальным графом — тем больше значение данной компоненты ортоцентра. Узлы сочленения имеют, как правило, отрицательные значения компонент связности. Поэтому барицентрические координаты ортоцентра
удобно называть вектором связности.Пример значений параметров для графа
Рассчитаем параметры популярного в Википедии графа.
Данный граф эквивалентен 6-вершинному симплексу в 5-мерном пространстве. Кружки с цифрами — это пронумерованные узлы графа. Силу связи между узлами (значение веса ребер) принимаем за единицу.
Геометрическая связность данного графа равна 1.663 — это средняя связность на один узел. Можно сравнить ее с максимальной (7.2) и минимальной (0.8) связностью для графа из 6 узлов. Индекс симметричности — 0.773.
Вектор связности узлов (барицентрические координаты ортоцентра): [0.364, 0.045, 0.273, -0.227, 0.045, 0.500]. Видим, что чем больше узел имеет связей, тем меньше значение его связности и наоборот. Отметим отрицательное значение связности 4-го узла. Это единственной узел графа, при удалении которого граф распадается на две несвязанные компоненты. Возможно, что компоненты с отрицательной связностью являются ключевыми узлами графа.
___
Подводим итоги. Определены взаимные метрические тензоры на элементах пространства, грамиан и лапласиан мажорного базиса. Показана связь симплексов и графов. В следующей статье покажем, как задавать координаты элементов в базисе.
