В первой статье определен метрический базис на элементах, — набор вершин симплекса или графа с известными значениями скалярных произведений (грамиан) или связей (лапласиан) между ними. Здесь рассмотрим, как на таком базисе определить координаты элементов.

Дистанционные координаты представляют собой значения скалярных произведений элемента и реперов — вершин базиса. Будем именовать их ди-координатами.
Количество компонент ди-координат на единицу больше количества базовых вершин и на две единицы больше мерности пространства базиса
и на две единицы больше мерности пространства базиса  . Примером ди-координат может служить строка (или колонка) дистанционного метрического тензора (ДМТ).
. Примером ди-координат может служить строка (или колонка) дистанционного метрического тензора (ДМТ).
Дистанционные координаты элемента будем обозначать как , в тензорной форме — нижним индексом, указывающем на базис:
, в тензорной форме — нижним индексом, указывающем на базис:  . Если надо будет указать, к какому именно элементу относятся координаты, то используем скобки:
. Если надо будет указать, к какому именно элементу относятся координаты, то используем скобки:  .
.
Полный базис включает в себя нормаль пространства (является мажорным), — соответственно в ди-координатах можно выделить скалярную единицу (произведение элемента и нормали) и набор скалярных произведений элемента и вершин базиса :
:
![$dm=[1; d]$](https://habrastorage.org/getpro/habr/formulas/177/1e2/554/1771e25545218314f5baf0b2d21bd40b.svg) .
.
Набор скалярных произведений будем называть также минорными компонентами.
будем называть также минорными компонентами.
Приведем примеры значений дистанционных координат. Допустим, рядом с нашим базовым треугольником есть еще три точки с известными дистанциями до вершин треугольника — P, Q и R (см. рисунок). Для расчета дистанций используем декартовы координаты точек на плоскости (XY), которые приводим для контроля и сверки:
Кортеж дистанций от точки P до точек A, B, С здесь такой:![$[2, 5, 26]$](https://habrastorage.org/getpro/habr/formulas/f52/638/bda/f52638bda6b81cd285c96a397ed325e6.svg) . Соответственно ди-координаты точки будут такими:
. Соответственно ди-координаты точки будут такими: ![$dm(P)=[1; -1.0, -2.5, -13.0]$](https://habrastorage.org/getpro/habr/formulas/80b/119/d02/80b119d02b696b8e92e35c9cf48b558a.svg) . У всех точек пространства значение скалярной компоненты ди-координат одно и то же (в рамках данной серии статей).
. У всех точек пространства значение скалярной компоненты ди-координат одно и то же (в рамках данной серии статей).
Ди-координаты точек Q и R:
![$dm(Q)=[1; -6.5, -2.0, -6.5]$](https://habrastorage.org/getpro/habr/formulas/c59/58e/f82/c5958ef8276b17e3794ea5c1a87136b7.svg)
![$dm(R)=[1; -12.5, -2.0, -20.5]$](https://habrastorage.org/getpro/habr/formulas/6a5/e36/186/6a5e3618699d1e1a3ce45c0d407d28ac.svg)
Разность элементов задает вектор. У ди-координат вектора скалярная компонента равна нулю — по этому признаку вектор можно отличить от элемента.
можно отличить от элемента.
Геометрия, в которой описание координат точек и векторов отличается, называется аффинной. В такой геометрии вектор можно прибавить к какому-либо элементу (точке) и получить новый элемент. Для векторов определены операции сложения и вычитания (значение скалярной компоненты при этом остается нулевым). Но обычно нет смысла в операции сложения элементов.
Несложно показать, что метрическим тензором для дистанционных координат является лапласиан (ЛМТ). Для определения квадрата расстояния (дистанции) между элементами P и Q надо найти вектор разности элементов и рассчитать его норму. Норма вектора определяется через билинейную форму — умножение координат вектора слева и справа и на метрический тензор. Для дистанционных координат это записывается так:
и рассчитать его норму. Норма вектора определяется через билинейную форму — умножение координат вектора слева и справа и на метрический тензор. Для дистанционных координат это записывается так:

где — ди-координаты вектора,
— ди-координаты вектора,  — лапласовский метрический тензор.
— лапласовский метрический тензор.
Проверяем. Координаты искомого вектора:![$dm(P-Q) = [1; -6.5, -2.0, -6.5] - [1; -1.0, -2.5, -13.0] = [0; -5.5, 0.5, 6.5]$](https://habrastorage.org/getpro/habr/formulas/4c9/d9e/c93/4c9d9ec9340a27a818f0f8877b0127fe.svg) . Данные координаты умножаем с двух сторон на лапласовский метрический тензор (ЛМТ) и получаем ответ:
. Данные координаты умножаем с двух сторон на лапласовский метрический тензор (ЛМТ) и получаем ответ:  . Можно свериться с расчетом расстояния через дистанции в декартовых координатах:
. Можно свериться с расчетом расстояния через дистанции в декартовых координатах:  . Ответы совпали, метрика работает.
. Ответы совпали, метрика работает.
Симплекс из вершин определяет
вершин определяет  -мерное пространство
-мерное пространство  . Базисный треугольник определяет базовую плоскость
. Базисный треугольник определяет базовую плоскость  . Количество дистанционных компонент в ди-координатах элемента на единицу больше мерности пространства. Это означает, что ди-координаты позволяют задавать элементы, выходящие за пределы базового пространства и принадлежащие
. Количество дистанционных компонент в ди-координатах элемента на единицу больше мерности пространства. Это означает, что ди-координаты позволяют задавать элементы, выходящие за пределы базового пространства и принадлежащие  . В нашем примере элементы могут лежать не только в плоскости базового треугольника, но и на (под) ним.
. В нашем примере элементы могут лежать не только в плоскости базового треугольника, но и на (под) ним.
Координаты элемента не позволяют определить, с какой стороны базового пространства находится элемент (если он находится вне). В примере с треугольником элементы, расположенные над и под плоскостью треугольника, будут иметь одни и те же координаты.

Если элемент не принадлежит базовому пространству, то следует различать положение элемента и его проекции на пространство
и его проекции на пространство  . Формула дистанции между элементами (2.1) работает только в базовом пространстве (поэтому в ней дистанция помечена штрихом), то есть определяет квадрат расстояния между проекциями элементов (а не между самими элементами):
. Формула дистанции между элементами (2.1) работает только в базовом пространстве (поэтому в ней дистанция помечена штрихом), то есть определяет квадрат расстояния между проекциями элементов (а не между самими элементами):

Здесь через индекс обозначен базис, на пространство которого проецируется дистанция между элементами. В декартовых (и подобных им) координатах нет способа задания координат элементов, выходящих за него. Поэтому в декартовой системе координат таких нюансов нет.
обозначен базис, на пространство которого проецируется дистанция между элементами. В декартовых (и подобных им) координатах нет способа задания координат элементов, выходящих за него. Поэтому в декартовой системе координат таких нюансов нет.
Раскрывая скобки в формуле (2.1), получаем «теорему косинусов для элементов». По форме она похожа на обычную , только здесь у нас координаты элементов (а не векторов). Поэтому нет ни углов, ни косинусов. Зато получаем определения норм элементов относительно базиса:



Скаляр будем называть нормой элемента, а скаляр
будем называть нормой элемента, а скаляр  — скалярным произведением элементов. Здесь скалярное произведение выражено через билинейную форму.
— скалярным произведением элементов. Здесь скалярное произведение выражено через билинейную форму.
Рассчитаем норму элемента , изображенного на рисунке. Умножая дважды ди-координаты элемента на метрический тензор ЛМТ, получаем ноль:
, изображенного на рисунке. Умножая дважды ди-координаты элемента на метрический тензор ЛМТ, получаем ноль:  . Что это значит?
. Что это значит?
Норма элемента характеризует его положение относительно базового пространства,- равна отрицательной дистанции от элемента до пространства:
 .
.
Значение нормы позволяет определить, принадлежит элемент пространству базиса или нет, и если нет, то насколько он от него удален.
Элементы с нулевой нормой удобно называть точками пространства — это локальные элементы. Элементы с ненулевой нормой — нелокальны относительно пространства базиса.
Геометрический смысл скалярного произведения векторов хорошо известен — отражает косинус угла между их направлениями.
Для интерпретации скалярного произведения элементов обратимся к формуле (2.2), (см. также рисунок проекций). Перегруппировав слагаемые, получим с учетом (2.4.1):

Видим, что удвоенное скалярное произведение представляет собой сумму дистанций от элементов до базового пространства и дистанции между проекциями элементов в базовом пространстве.
Обозначим через следующую комбинацию дистанций:
следующую комбинацию дистанций:

Данное выражение представляет собой скалярное произведение упорядоченных пар и
и  нормалей элементов к пространству. Теперь можно выразить произведение элементов через дистанцию между ними и произведение нормалей:
нормалей элементов к пространству. Теперь можно выразить произведение элементов через дистанцию между ними и произведение нормалей:

Данная формула позволяет определять дистанции до элементов вне пространства базиса.
Если скалярное произведение нормалей равно нулю (например, один из элементов принадлежит пространству базиса), то дистанция между элементами определяется их скалярным произведением:
(например, один из элементов принадлежит пространству базиса), то дистанция между элементами определяется их скалярным произведением:

Формула (2.6.1) раскрывает смысл скалярного произведения элементов — оно отражает квадрат расстояния между элементами с коэффициентом (-1/2).
Если элементы находятся вне базового пространства, то для определения точной дистанции между ними помимо координат требуется дополнительная информация — а именно значение скалярного произведения нормалей на пространство . Данное скалярное произведение можно вычислить при условии, что элементы принадлежат одному и тому же надпространству. В этом случае скалярное произведение между нормалями элементов — это просто произведение их длин. Тогда «магическая» формула вычисления дистанции между нелокальными элементами будет такой:
. Данное скалярное произведение можно вычислить при условии, что элементы принадлежат одному и тому же надпространству. В этом случае скалярное произведение между нормалями элементов — это просто произведение их длин. Тогда «магическая» формула вычисления дистанции между нелокальными элементами будет такой:

Значение скаляра равно 1, если элементы расположены с одной стороны пространства и -1, если с разных. Данная формула — просто частный (но важный) случай тождества (2.6). Во многих прикладных задачах расположение элементов всегда одностороннее, поэтому формула (2.7) может быть использована для определения дистанции между объектами (находящимися, например, в воздухе) если известны их ди-координаты относительно реперов (радаров на земле).
равно 1, если элементы расположены с одной стороны пространства и -1, если с разных. Данная формула — просто частный (но важный) случай тождества (2.6). Во многих прикладных задачах расположение элементов всегда одностороннее, поэтому формула (2.7) может быть использована для определения дистанции между объектами (находящимися, например, в воздухе) если известны их ди-координаты относительно реперов (радаров на земле).
Непросто представить, что, например, у 3-мерного пространства тоже есть сторона, но математика говорит, что есть. В декартовых координатах сторона, которой принадлежит элемент, определяется знаком значения n-ой компоненты, которая не входит в базовые. Если тетраэдр задан в декартовых координатах x, y, z, и при этом еще существует одна компонента (например, t — время), то можно считать, что плоскость t=0 делит базовое пространство на две стороны. Элементы, у которых компонента t > 0, лежат с одной стороны базового пространства, а у которых t < 0 — с другой.
Взаимными по отношению к дистанционным координатам являются би-координаты элемента. Термин связан с тем, что би-координаты фактически представляют собой расширение барицентрических координат. Метрическим тензором для би-координат является дистанционный тензор.
Би-координаты элемента обозначаются в тензорной форме верхним индексом . Переход от ди-координат к би-координатам (и обратно) выполняется умножением на соответствующий метрический тензор базиса:
. Переход от ди-координат к би-координатам (и обратно) выполняется умножением на соответствующий метрический тензор базиса:

Рассчитаем би-координаты элемента P относительно вершин нашего треугольника. Выполняя умножение ЛМТ на ди-координаты элемента, получаем:
![$bm^i=Lm^{ij} dm_j=[-3/2; 11/12, 1/3, -1/4]$](https://habrastorage.org/getpro/habr/formulas/db3/be4/fa2/db3be4fa20a2a20dd71eed289dc64d69.svg)
Особенность барицентрических координат в том, что сумма их компонент равна 1 (в нашем примере 11/12 + 1/3 — 1/4 = 1). Каждая барицентрическая компонента — это вклад (вес) вершины базиса в координату элемента. Чем больше значение компоненты — тем ближе находится элемент к базовой вершине.
Структура би-координат может быть записана как:![$bm = [w; b] $](https://habrastorage.org/getpro/habr/formulas/584/ee6/0c0/584ee60c00b380dd6eaba492e353e759.svg) .
.
Здесь — барицентрические координаты, а
— барицентрические координаты, а  — орбиталь элемента. Орбиталь отражает скалярное произведение элемента и ортоцентра базиса
— орбиталь элемента. Орбиталь отражает скалярное произведение элемента и ортоцентра базиса  :
:

В геометрии есть понятие степени точки — положение точки относительно заданной сферы. Задается как разность между дистанцией от точки до центра сферы
— положение точки относительно заданной сферы. Задается как разность между дистанцией от точки до центра сферы  и радиусом сферы
и радиусом сферы  :
:

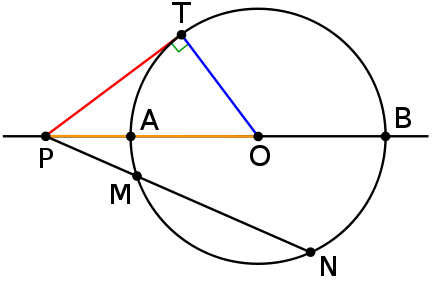
На рисунке квадрат длины катета треугольника
треугольника  (от точки до касания сферы) равен значению степени точки P. Точки M и N на рисунке демонстрируют полезное свойство степени, а именно, что ее значение равно произведению длин отрезков
(от точки до касания сферы) равен значению степени точки P. Точки M и N на рисунке демонстрируют полезное свойство степени, а именно, что ее значение равно произведению длин отрезков  и
и  .
.
Орбиталь элемента может быть выражена через степень элемента относительно ортоцентра:
 .
.
Если орбиталь больше нуля — элемент лежит внутри ортоцентра (сферы) базиса, если меньше — снаружи. Барицентрические координаты характеризуют положение проекции элемента в пространстве базового симплекса, а скалярная компонента — задает пространственное положение относительно ортоцентра.
характеризуют положение проекции элемента в пространстве базового симплекса, а скалярная компонента — задает пространственное положение относительно ортоцентра.
Орбиталь вершин базиса равна нулю (поскольку элементы базиса принадлежат поверхности базисной сферы). Би-координаты вершин базиса представляют собой единичные координаты (с единицей в своей базисной компоненте и нулем в остальных — обычно обозначаются как ). Например, би-координаты вершины A треугольника будут равны [0; 1, 0, 0].
). Например, би-координаты вершины A треугольника будут равны [0; 1, 0, 0].
Если элемент не принадлежит пространству базиса, то его дистанция до ортоцентра равна сумме дистанций от элемента до его проекции
равна сумме дистанций от элемента до его проекции  и дистанции от проекции до центра
и дистанции от проекции до центра  . Первая равна норме элемента с обратным знаком. Тогда можно выразить орбиталь элемента через орбиталь его проекции
. Первая равна норме элемента с обратным знаком. Тогда можно выразить орбиталь элемента через орбиталь его проекции  и норму
и норму  :
:

В свою очередь орбиталь проекции можно определить через би-линейную форму барицентрических координат элемента и минорного грамиана базиса :
:

В 5-й части покажем, что понятие орбитали элемента относительно ортоцентра можно обобщить до определения взаимной орбитали элементов. Которое в свою очередь связано с понятием скалярного произведения векторов.
Как и в случае ди-координат следует отличать би-координаты элемента от би-координат вектора разности элементов (аффинная геометрия). Однако критерий отличия двух типов координат в данной системе иной. Сумма барицентрических компонент элемента равна 1, а сумма компонент вектора будет равна 0 (поскольку разность) — балансовые векторы. (Балансовые векторы используются в проводках бухгалтерского учета). Остальное аналогично. Би-векторы можно складывать и вычитать — при этом результат остается в пространстве векторов.
Орбиталь (скалярная компонента би-координат) вектора отражает величину проекции ортоцентра базиса на вектор. Не зависит от нормы ортоцентра (квадрата радиуса сферы).
Би-координаты ортоцентра образуют окаймление лапласовского метрического тензора. Вспоминая, что сумма компонент лапласиана равна нулю, можно заключить, что строки (колонки) лапласиана базиса отражают би-координаты неких векторов. Это векторы дуального базиса, здесь на них подробно не останавливаемся.
Скалярная компонента добавляет метрику к барицентрическим координатам. При наличии известного метрического тензора (ДМТ) можно вычислять дистанции между элементами, принадлежащими базовому пространству. Все стандартно — через билинейную форму умножения разности координат на метрический тензор. Формулы аналогичны выражениям в ди-координатах с заменой метрического тензора на
на  и ди-координат
и ди-координат  на би-координаты
на би-координаты  . Обозначив би-координаты вектора разности элементов как
. Обозначив би-координаты вектора разности элементов как  , получаем:
, получаем:
Дистанция между проекциями:
Норма элемента:
Скалярное произведение:
Знание би-координат элементов и их положения относительно базового пространства также позволяет вычислять дистанцию между элементами вне базового пространства по формуле (2.6). И это круто. Обычно считается, что барицентрические координаты задают лишь относительное положение элементов. Оказывается, что если добавить к ним скалярную компоненту в виде орбитали, то можно определять пространственное положение не только самого элемента, но и дистанции между элементами вне базового пространства.
Как уже отмечалось, в полный (мажорный) набор элементов базиса входит вектор нормали пространства . Ди-координаты нормали имеют вид: [0; 1, 1,...]. Соответственно, би-координаты нормали взаимно обратны: [1; 0, 0,...]. Ди-координаты вектора нормали входят в структуру дистанционного метрического тензора.
. Ди-координаты нормали имеют вид: [0; 1, 1,...]. Соответственно, би-координаты нормали взаимно обратны: [1; 0, 0,...]. Ди-координаты вектора нормали входят в структуру дистанционного метрического тензора.
О том, что нормаль это вектор, говорит значение нуля в скалярной компоненте ди-координат и равенство нулю суммы барицентрических координат.
Норма нормали (свертка ди- и би-координат) всегда равна нулю, поскольку проекция нормали на любое пространство всегда будет точкой.
Как следствие, — нормаль пространства можно прибавлять к элементам. Такая операция изменяет норму элемента, но не его положение в пространстве. Зная координаты проекции элемента и норму
и норму  , всегда можно определить координаты самого элемента
, всегда можно определить координаты самого элемента  . Для этого вектор нормали умножаем на полунорму элемента и прибавляем полученный вектор к координатам проекции.
. Для этого вектор нормали умножаем на полунорму элемента и прибавляем полученный вектор к координатам проекции.

Если в формуле связи ди- и би-координат (2.8) раскрыть структуру умножаемых матриц и векторов, то можно получить полезные тождества для скалярной и минорной компонент координат. Для би-координат имеем:

Здесь — минорные ди- и би-координаты элементов. Таким образом:
— минорные ди- и би-координаты элементов. Таким образом:


Выражение (2.12.1) демонстрирует, что результат действия лапласиана на вектор можно интерпретировать как вектор разности элемента и ортоцентра.
Тождество (2.12.2) (при выводе использовано также (2.9) и (2.10)) показывает, как зная минорную составляющую ди-координат, получить ее степень и дистанцию до ортоцентра.
Перейдем к структуре ди-координат:

Откуда:


Первое тождество показывает, что сумма барицентрических компонент равна 1, это и так знали (но тут видно почему — потому что используем единичный вектор в качестве окаймления дистанционной матрицы).
Второе показывает роль орбитали в дистанционных координатах. Дистанционный вектор складывается из весовой суммы дистанционных векторов вершин базиса
складывается из весовой суммы дистанционных векторов вершин базиса  и вектора нормали к базовому пространству, величина которого задается орбиталью элемента.
и вектора нормали к базовому пространству, величина которого задается орбиталью элемента.
Используя скалярное произведение координат обоих типов (би- и ди-), можно избавиться в формулах от метрических тензоров.
Дистанция между проекциями:
Норма элемента:
Скалярное произведение:
Кратко перечислим основные определения.
 — ди-координаты элемента, набор скалярных произведений элемента и реперов базиса,
— ди-координаты элемента, набор скалярных произведений элемента и реперов базиса,
 — би-координаты элемента, коэффициенты линейного разложения элемента по реперам базиса,
— би-координаты элемента, коэффициенты линейного разложения элемента по реперам базиса,
Изменение типа координат (от ди- к би- и обратно) («жонглирование индексами») выполняется умножением на соответствующий метрический тензор:

Скалярное произведение элементов:

 — вектор, разность элементов,
— вектор, разность элементов,
Норма вектора разности — дистанция между проекциями элементов на пространство базиса:

___
В следующей статье рассмотрим скалярное произведение упорядоченных пар.
Оглавление
1. Симплексы и графы
2. Определение ди- и би-координат
3. Скалярное произведение пар
4. Пространство графа
5. Преобразование базиса
6. Граф-звезда
2. Определение ди- и би-координат
3. Скалярное произведение пар
4. Пространство графа
5. Преобразование базиса
6. Граф-звезда

Дистанционные координаты
Дистанционные координаты представляют собой значения скалярных произведений элемента и реперов — вершин базиса. Будем именовать их ди-координатами.
Количество компонент ди-координат на единицу больше количества базовых вершин
Дистанционные координаты элемента будем обозначать как
Полный базис включает в себя нормаль пространства (является мажорным), — соответственно в ди-координатах можно выделить скалярную единицу (произведение элемента и нормали) и набор скалярных произведений элемента и вершин базиса
Набор скалярных произведений
Приведем примеры значений дистанционных координат. Допустим, рядом с нашим базовым треугольником есть еще три точки с известными дистанциями до вершин треугольника — P, Q и R (см. рисунок). Для расчета дистанций используем декартовы координаты точек на плоскости (XY), которые приводим для контроля и сверки:
Матрица декартовых координат точек:
\begin{array}{c | c c c c c c}
XY & A & B & C & P & Q & R \\
\hline
X & 0 & 3 & 0 & 1 & 3 & 5 \\
Y & 0 & 0 & 4 &-1 & 2 & 0 \\
\end{array}
XY & A & B & C & P & Q & R \\
\hline
X & 0 & 3 & 0 & 1 & 3 & 5 \\
Y & 0 & 0 & 4 &-1 & 2 & 0 \\
\end{array}
Кортеж дистанций от точки P до точек A, B, С здесь такой:
Ди-координаты точек Q и R:
Элементы и векторы
Разность элементов задает вектор. У ди-координат вектора скалярная компонента равна нулю — по этому признаку вектор
Геометрия, в которой описание координат точек и векторов отличается, называется аффинной. В такой геометрии вектор можно прибавить к какому-либо элементу (точке) и получить новый элемент. Для векторов определены операции сложения и вычитания (значение скалярной компоненты при этом остается нулевым). Но обычно нет смысла в операции сложения элементов.
Термин <вектор> перегружен.
В мире (линейной) алгебры обычно под векторным пространством понимают некое линейное пространство, в котором элементы характеризуются набором чисел, и определены операции сложения и вычитания.
В таком пространстве нет различия между элементами и векторами — «все вектор».
В нашем пространстве это не так.
В таком пространстве нет различия между элементами и векторами — «все вектор».
В нашем пространстве это не так.
Дистанция между элементами
Несложно показать, что метрическим тензором для дистанционных координат является лапласиан (ЛМТ). Для определения квадрата расстояния (дистанции) между элементами P и Q надо найти вектор разности элементов
где
Проверяем. Координаты искомого вектора:
Для проверки расчетов приводим значение ЛМТ нашего базиса из предыдущей статьи
\begin{array}{c | c c c c}
Lm(A,B,C) & * & A & B & C \\
\hline
* & 6.25 & 0 & 0.5 & 0.5 \\
A & 0 & 25/144 & -16/144 & -9/144 \\
B & 0.5 & -16/144 & 16/144 & 0 \\
C & 0.5 & -9/144 & 0 & 9/144 \\
\end{array}
Lm(A,B,C) & * & A & B & C \\
\hline
* & 6.25 & 0 & 0.5 & 0.5 \\
A & 0 & 25/144 & -16/144 & -9/144 \\
B & 0.5 & -16/144 & 16/144 & 0 \\
C & 0.5 & -9/144 & 0 & 9/144 \\
\end{array}
Элемент и его проекция на базовое пространство
Симплекс из
Координаты элемента не позволяют определить, с какой стороны базового пространства находится элемент (если он находится вне). В примере с треугольником элементы, расположенные над и под плоскостью треугольника, будут иметь одни и те же координаты.

Если элемент не принадлежит базовому пространству, то следует различать положение элемента
Здесь через индекс
Норма элемента и дистанция до базового пространства
Раскрывая скобки в формуле (2.1), получаем «теорему косинусов для элементов». По форме она похожа на обычную , только здесь у нас координаты элементов (а не векторов). Поэтому нет ни углов, ни косинусов. Зато получаем определения норм элементов относительно базиса:
Скаляр
Рассчитаем норму элемента
Норма элемента характеризует его положение относительно базового пространства,- равна отрицательной дистанции от элемента до пространства:
Значение нормы позволяет определить, принадлежит элемент пространству базиса или нет, и если нет, то насколько он от него удален.
Элементы с нулевой нормой удобно называть точками пространства — это локальные элементы. Элементы с ненулевой нормой — нелокальны относительно пространства базиса.
Скалярное произведение элементов
Геометрический смысл скалярного произведения векторов хорошо известен — отражает косинус угла между их направлениями.
Для интерпретации скалярного произведения элементов обратимся к формуле (2.2), (см. также рисунок проекций). Перегруппировав слагаемые, получим с учетом (2.4.1):
Видим, что удвоенное скалярное произведение представляет собой сумму дистанций от элементов до базового пространства и дистанции между проекциями элементов в базовом пространстве.
Обозначим через
Данное выражение представляет собой скалярное произведение упорядоченных пар
Данная формула позволяет определять дистанции до элементов вне пространства базиса.
Если скалярное произведение нормалей равно нулю
Формула (2.6.1) раскрывает смысл скалярного произведения элементов — оно отражает квадрат расстояния между элементами с коэффициентом (-1/2).
Дистанция между элементами вне базисного пространства
Если элементы находятся вне базового пространства, то для определения точной дистанции между ними помимо координат требуется дополнительная информация — а именно значение скалярного произведения нормалей на пространство
Значение скаляра
Непросто представить, что, например, у 3-мерного пространства тоже есть сторона, но математика говорит, что есть. В декартовых координатах сторона, которой принадлежит элемент, определяется знаком значения n-ой компоненты, которая не входит в базовые. Если тетраэдр задан в декартовых координатах x, y, z, и при этом еще существует одна компонента (например, t — время), то можно считать, что плоскость t=0 делит базовое пространство на две стороны. Элементы, у которых компонента t > 0, лежат с одной стороны базового пространства, а у которых t < 0 — с другой.
Би-координаты
Взаимными по отношению к дистанционным координатам являются би-координаты элемента. Термин связан с тем, что би-координаты фактически представляют собой расширение барицентрических координат. Метрическим тензором для би-координат является дистанционный тензор.
Би-координаты элемента обозначаются в тензорной форме верхним индексом
Рассчитаем би-координаты элемента P относительно вершин нашего треугольника. Выполняя умножение ЛМТ на ди-координаты элемента, получаем:
Особенность барицентрических координат в том, что сумма их компонент равна 1 (в нашем примере 11/12 + 1/3 — 1/4 = 1). Каждая барицентрическая компонента — это вклад (вес) вершины базиса в координату элемента. Чем больше значение компоненты — тем ближе находится элемент к базовой вершине.
Орбиталь элемента
Структура би-координат может быть записана как:
Здесь
В геометрии есть понятие степени точки

На рисунке квадрат длины катета
Орбиталь элемента может быть выражена через степень элемента относительно ортоцентра:
Если орбиталь больше нуля — элемент лежит внутри ортоцентра (сферы) базиса, если меньше — снаружи. Барицентрические координаты
Орбиталь вершин базиса равна нулю (поскольку элементы базиса принадлежат поверхности базисной сферы). Би-координаты вершин базиса представляют собой единичные координаты (с единицей в своей базисной компоненте и нулем в остальных — обычно обозначаются как
Если элемент не принадлежит пространству базиса, то его дистанция до ортоцентра
В свою очередь орбиталь проекции можно определить через би-линейную форму барицентрических координат элемента и минорного грамиана базиса
В 5-й части покажем, что понятие орбитали элемента относительно ортоцентра можно обобщить до определения взаимной орбитали элементов. Которое в свою очередь связано с понятием скалярного произведения векторов.
Би-координаты элементов и векторов
Как и в случае ди-координат следует отличать би-координаты элемента от би-координат вектора разности элементов (аффинная геометрия). Однако критерий отличия двух типов координат в данной системе иной. Сумма барицентрических компонент элемента равна 1, а сумма компонент вектора будет равна 0 (поскольку разность) — балансовые векторы. (Балансовые векторы используются в проводках бухгалтерского учета). Остальное аналогично. Би-векторы можно складывать и вычитать — при этом результат остается в пространстве векторов.
Орбиталь (скалярная компонента би-координат) вектора отражает величину проекции ортоцентра базиса на вектор. Не зависит от нормы ортоцентра (квадрата радиуса сферы).
Би-координаты ортоцентра образуют окаймление лапласовского метрического тензора. Вспоминая, что сумма компонент лапласиана равна нулю, можно заключить, что строки (колонки) лапласиана базиса отражают би-координаты неких векторов. Это векторы дуального базиса, здесь на них подробно не останавливаемся.
Дистанция и нормы в би-координатах
Скалярная компонента добавляет метрику к барицентрическим координатам. При наличии известного метрического тензора (ДМТ) можно вычислять дистанции между элементами, принадлежащими базовому пространству. Все стандартно — через билинейную форму умножения разности координат на метрический тензор. Формулы аналогичны выражениям в ди-координатах с заменой метрического тензора
Дистанция между проекциями:
Норма элемента:
Скалярное произведение:
Знание би-координат элементов и их положения относительно базового пространства также позволяет вычислять дистанцию между элементами вне базового пространства по формуле (2.6). И это круто. Обычно считается, что барицентрические координаты задают лишь относительное положение элементов. Оказывается, что если добавить к ним скалярную компоненту в виде орбитали, то можно определять пространственное положение не только самого элемента, но и дистанции между элементами вне базового пространства.
Объединяем ди- и би-координаты
Нормаль к пространству — особый вектор
Как уже отмечалось, в полный (мажорный) набор элементов базиса входит вектор нормали пространства
О том, что нормаль это вектор, говорит значение нуля в скалярной компоненте ди-координат и равенство нулю суммы барицентрических координат.
Норма нормали (свертка ди- и би-координат) всегда равна нулю, поскольку проекция нормали на любое пространство всегда будет точкой.
Как следствие, — нормаль пространства можно прибавлять к элементам. Такая операция изменяет норму элемента, но не его положение в пространстве. Зная координаты проекции элемента
Связь параметров базиса с координатами элементов
Если в формуле связи ди- и би-координат (2.8) раскрыть структуру умножаемых матриц и векторов, то можно получить полезные тождества для скалярной и минорной компонент координат. Для би-координат имеем:
Здесь
Выражение (2.12.1) демонстрирует, что результат действия лапласиана на вектор можно интерпретировать как вектор разности элемента и ортоцентра.
Тождество (2.12.2) (при выводе использовано также (2.9) и (2.10)) показывает, как зная минорную составляющую ди-координат, получить ее степень и дистанцию до ортоцентра.
Перейдем к структуре ди-координат:
Откуда:
Первое тождество показывает, что сумма барицентрических компонент равна 1, это и так знали (но тут видно почему — потому что используем единичный вектор в качестве окаймления дистанционной матрицы).
Второе показывает роль орбитали в дистанционных координатах. Дистанционный вектор
Нормы — это свертка координат разных типов
Используя скалярное произведение координат обоих типов (би- и ди-), можно избавиться в формулах от метрических тензоров.
Дистанция между проекциями:
Норма элемента:
Скалярное произведение:
Собираем все вместе
Кратко перечислим основные определения.
Изменение типа координат (от ди- к би- и обратно) («жонглирование индексами») выполняется умножением на соответствующий метрический тензор:
Скалярное произведение элементов:
Норма вектора разности — дистанция между проекциями элементов на пространство базиса:
___
В следующей статье рассмотрим скалярное произведение упорядоченных пар.