Comments 53
Впечатляет. Я пару лет назад делал нечто подобное на pgrouting, и там используется двунаправленный Дейкстра, вероятно, неспроста. Неплохо было бы здесь его добавить в сравнение. Ещё можно было бы и BFS/DFS включить для наглядности...
Можно было бы попробовать сжать gzip'ом — карта Москвы из 47МБ превращается в 7.1МБ. Но при таком подходе у меня не было бы контроля над скоростью распаковки данных — их бы пришлось парсить javascript'ом на клиенте, что тоже повлияло бы на скорость инициализации.
gzip распаковывается браузером.
Это не самый эффективный способ сжатия, но его очень легко реализовать и можно очень быстро восстановить начальный граф на клиенте.
Ну а на сколько эффективнее (меньше) получилось чем JSON, XML/gzip?
Вы правы. Меня больше смущало отсутствие потокового парсинга JSON'a. Ну и потом, работа напрямую с типизрованными массивами потенциально дает возможность загнать данные сразу в видеобуфер. Не то, чтобы я это делал, но все же :)… Впрочем, глядя критично на вещи, не исключено что я тут чуть-чуть занялся велосипедостроительством и преждевременной оптимизацией.
> Ну а на сколько эффективнее (меньше) получилось чем JSON, XML/gzip?
Карта Москвы из 7.1МБ превратилась в 6.5МБ. Не сильно
Хороший вопрос! Я когда-то считал pagerank в javascript'e и ради интереса написал алгоритм на asm.js и на типизированных массивах. Только что проверил на node 7.2.1, asm.js все еще медленнее чем типизированные массивы раза в пять (60 операций в секунду против 12). Мозиловский javascript движок, конечно, выигрывал на asm.js версии, когда проверял его несколько лет назад
Там своя стековая машина беспощадная к ошибкам.
В Вашем случае алгоритм строит не кратчайший путь, а быстро его строит. Собственно, Вы так и написали. Было бы интересно сравнить точность и время работы.
Это не совсем верно. Все поисковики в моей библиотеке находят кратчайший путь, за исключением A* greedy.
Алгоритм Дейкстры — это частный случай алгоритма A* — просто функция эвристика всегда отдает 0.
Я так понял DaylightIsBurning сказал что 20-50ms будет скорость поиска кратчайшего пути, если использовать WebAssembly — потому мне хотелось узнать подробнее о методе/коде.
20-50ms будет скорость поиска кратчайшего пути, если использовать WebAssemblyПо сути да, а точнее — полный просчёт SSSP задачи алгоритмом Дейкстры, и не WebAssembly, а нативный код. Я писал для себя маленькую функцию на C++ для этих целей (адаптированый копи-паст из гугла). В моём случае графы были с числом узлов ~110k и числом связей ~15*110k. На одном ядре i7-4930K получалось 20-30ms. В моём случае это были grid-графы на трёхмерной решётке. При этом глубина связывания была больше 1 (то есть не только 27 ближайших соседей рассматривалось но и часть второй коорд. сферы).
Код не идеальный, но если Вам интересно, то вот (главное в pathLength).
(|E| + |V|)*log|V|*6 тактов, что для моего CPU даст
(730000 + 260000)*log2(260000)*6 cycles /( 3.4*10^9 cycles/s) = 31.4 ms
У вас какие-то уж слишком оптимистичные оценки. Алгоритм дейкстры требует O(n log n + m log n) операций. Если подсчитать для этого графа, будет 17,820,000. Это надо умножить на константу — возьмем очень консервативно: 2. Т.е. у нас ~35 миллионов операций. Далеко не все из них тривиальные — там всякие скачки по указателям, сравнения. Если в среднем считать по 10 тактов на операцию, то при частоте в 3 Ghz это все займет 160 ms.
Для 20ms, как вы утверждаете, все операции должны занимать в среднем 1,25 такта, что просто невероятно. А это я еще константу маленькую взял. На практике, особенно в javascript'е оно будет в несколько раз больше.
Edges:13242707
Nodes:357911
Time Dijkstra: 78.862933 ms
Edges:13242707
Nodes:357911
Time Dijkstra: 87.523608 ms
Edges:13242707
Nodes:357911
Time Dijkstra: 63.876857 ms
Edges:8398297
Nodes:226981
Time Dijkstra: 37.649051 ms
Edges:8398297
Nodes:226981
Time Dijkstra: 37.884030 ms
Edges:8398297
Nodes:226981
Time Dijkstra: 38.607603 msВот выдрал соответствующую часть кода. Скачков по указателям почти нет т.к. граф и куча реализованы поверх std::vector.
Правильная производительность:
5.87181229 CPU cycles/operation=3.4*10^9 cycles/s*37.649051 ms/[(8398297/2+226981/2)operations*log(226981/2)]
То есть ещё можно оптимизировать. Пока что выходит не 20ms, но недалеко от моёй первой верхней оценки — 60-70ms.
(8398297+226981)*log(226981)=153462774.844
3.4*10^9Hz*37.649051 ms/153462774.844=0.83 операций на такт. Учитывая что так кеш-миссов нет — вполне нормально. Наверное, можно как-то еще SIMD задействовать, но я не представляю, как.
Я решил написать свой формат для графа. Граф разбивается на два бинарных файла. Один с координатами всех вершин, а второй с описанием всех ребер.
Файл с координатами — это просто последовательность из x, y пар (int32, 4 байта на координату). Смещение по которому находится пара координат я рассматриваю как иденификатор вершины (nodeId).
Вроде это CSR формат для хранения графов. Тут было встречал habrahabr.ru/post/214515
Два вопроса,
1. Есть где то место, где я бы смог по быстрому подменить ваш алгоритм на свой и проверить кто быстрей, ну так для спортивного интереса.
2. Планируется ли продолжение в виде продукта? Частенько от карт нужно быстро посмотреть маршрут между двумя точками и больше ничего, навигаторы и карты не то, что этого не позволяют, но слишком много действий, а нужно быстро.
Спасибо! Развитие в виде продукта я не планировал. А вот чтобы быстро подменить алгоритм нужно добавить его ключ/имя сюда, чтобы показывался в выпадающем списке. Потом для этого ключа нужно создать поисковик здесь — у поисковика только один метод find(fromNodeId, toNodeId), вернуть он должен массив узлов графа.
Можете также прислать ссылку на демо вашего алгоритма, если он публичный — я помогу потестировать.
У меня алгоритм вероятно чем то похож (но они все похожи) и так есть 2 стадии:
1. Максимально быстро найти первый путь до конечной точки
2. Проверить остальные варианты, до тех пор пока их расстояние меньше найденного.
В первой стадии, как быстро найти путь до конечной точки? (КО) Двигаться в ее направлении, то есть я сортировал все соседние точки по углу который между текущей точкой, конечной и соседней и первую очередь передвигался в сторону наименьшего угла между ними. Что бы не получилось вечного цикла, пройденные точки помечаются и повторном посещении, маршрут бракуется, алгоритм возвращается на шаг назад и проверяет остальные направления. Пока либо не переберет все точки до которых сможет добраться, либо не достигнет конечной точки.
Теперь если у нас есть первый маршрут, то маловероятно, что он самый оптимальный, поэтому алгоритм возвращается на шаг назад и проверяет нет ли более короткой дороги из предыдущей точки, в дополнение к проверкам из первой стадии, он проверяет что текущий маршрут не длинней уже найденного. Если длинней, дальше проверять нет смысла, дорог с отрицательной длинной нет. Если находится более короткий маршрут, то он заменяет тот первый. Все останавливается когда больше нет маршрута, который короче найденного.
код тут но он ужасен, в свое оправдание могу сказать только, что это было 15 лет назад, я его случайно нашел на старом сд с бекапом, когда перебирал кладовку :)
все ли до того как добраться до оценки было «выжато» из Дейкстры?
Я использовал тот же код что и для А* — просто эвристику в ноль поставил.
типа модели поиска минимального значения
Можете рассказать подробнее что это означает, пожалуйста?
типа модели поиска минимального значения
Можете рассказать подробнее что это означает, пожалуйста?
если в терминах псевдокода
1 function Dijkstra(Graph, source):
2
3 create vertex set Q
4
5 for each vertex v in Graph: // Initialization
6 dist[v] ← INFINITY // Unknown distance from source to v
7 prev[v] ← UNDEFINED // Previous node in optimal path from source
8 add v to Q // All nodes initially in Q (unvisited nodes)
9
10 dist[source] ← 0 // Distance from source to source
11
12 while Q is not empty:
13 u ← vertex in Q with min dist[u] // Node with the least distance will be selected first
14 remove u from Q
15
16 for each neighbor v of u: // where v is still in Q.
17 alt ← dist[u] + length(u, v)
18 if alt < dist[v]: // A shorter path to v has been found
19 dist[v] ← alt
20 prev[v] ← u
21
22 return dist[], prev[]то, например, реализация 13-я строчки
u ← vertex in Q with min dist[u]
для больших графов может очень сильно влиять на производительность всего алгоритма. В моем случае, использование в этом месте структуры данных «минимальной кучи» (min-heap) с алгоритмичской сложностью операции поиска минимального значения на уровне O(1), дал значительный прирост (на порядок) — даже не смотря на доп. издержки поддержания этой «кучи» при добавлении элементов.
Спасибо. Да, я тоже использую кучу для всех реализаций (включая Дейкстру)
Если речь идет о «турбо»
(ну… «как бы» турбо. Еще можно намутить свой распределитель памяти и вообще перейти на ассемблер — но это вопрос экономической целесообразности)
Я правильно понимаю, что вы задачу все-таки слегка упростили? Ну т.е., из overpass достается граф дорог, но потом вы удаляете тэги, показывающие, что это вот — велодорога или хайвей? И маршрут строится без учета того, какой у нас транспорт, и какой транспорт может двигаться по каждому из участка дороги? Или я что-то пропустил?
Примерно так. Вот запрос который я выполняю для получения дорог.
Маршрут действительно строится без весов.
А вы для какого ID его делаете для Нью-Йорка? Я попробовал для id 3600175905 ("New York City") и получил только 50000 ребер и 195000 вершин.
200мс — это чудовищно, отвратительно медленно. Я верю что это число можно уменьшить по меньшей мере раз в десять просто переписав код один в один на любом из более нормальных языков программирования. А немножко пооптимизировав и во все пятьдесят.
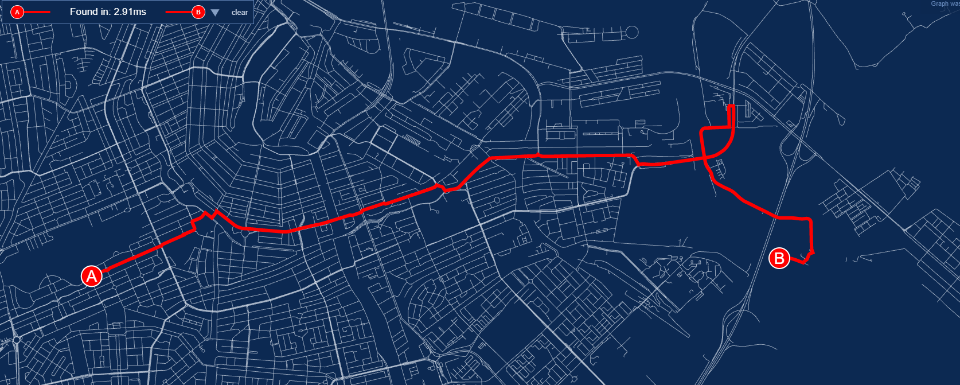
Мне кажется, я видел эту петлю на гуглокартах — есть подозрение что это единственный путь к точке B
Если вы любите такие задачи, то могу подкинуть насущную проблему, которую в мире js никто ещё не решил. Это реализация бесконечного скрола. Не для конкретного случая, а универсальная. Т.е. динамически подгружаеммый с сервера массив данных, которые рендерятся в дом-элементы произвольной высоты, которая к тому же может динамически менятся. Это могут быть как строки, так и плитка и т.п. Состав элементов так же может меняться (какие-то удаляться, какие-то добавляться). Ну и методы для скролла к произвольному элементу, к началу, к концу. Разумеется, всё это должно шустро работать в современных браузерах и не прыгать по странице. Сделаете — будет вам вечный респект от js мира
Проблема с бесконечным скролом интересная, конечно! Увы, у меня сейчас другие приоритеты.
Если вы на реакте пишете, то вот эта библиотека выглядит очень многообещающе: github.com/bvaughn/react-virtualized
Увидел у вас на github страничке, что вы пытались сделать двунаправленный A*, но он был не оптимальный. У меня была похожая проблема, главное правильно выбирать, когда встречаются дороги, т.е. важен порядок какую ветку сейчас надо рассматривать от начала или от конца. Так же очень важно не завершать работу алгоритма, когда найдена точка соприкосновения, а необходимо выполнения условия, что найденный маршрут короче суммы стоимости оставшихся дорог из очередей.
К сожалению, не могу поверить, что NBA* будет быстрее, чем двунаправленный A*, потому что «эвристика» (неправильно называть эвристика так как если она меньше 1, то она всегда находит оптимальный маршрут) направляет построение маршрута.
Еще маленькое замечание, оптимизации самого движка построения маршрута вещь необходимая для конечного продука, но сам алгоритм желательно проверять масштабированием. Грубо говоря, насколько становится медленным если перейти от 10К edge к 100К. Или сколько занимает времени построить 10 км маршрут, 100 км, 1000 км.
Спасибо за дельный совет!
NBA* и есть двунаправленный А*, его особенность в том, что он делает после того как оба поиска встретились, и в том, как он учитывает эвристики с противоположной стороны поиска. Когда поиск вперед раздумывает зайти ли в узел или нет, он так же смотрит на эвристику обратного поиска — здесь f2 инициализровано обратным поиском. Доказательство корректности можно найти здесь: https://repub.eur.nl/pub/16100/ei2009-10.pdf
R, S — priority queues forward & backward.
f — calculated route time function
h — heuristic function — h(x, y) = min_time(x, y) * h // обязательно, что h <= 1 и маршрут между x, y всегда меньше, чем min_time(x,y), на практике min_time = distance / max_possible_speed
R = priorityQueue | f(x) + h(x, end)
Q = priorityQueue | h(start, x) + f(x)
queue = R
while(!queue.isEmpty()) {
Edge start = queue.poll()
for(Edge e : exploreAllOutgoingEdges(start)) {
Edge s = visitedOppositeEdges.get(e)
if(s != null){
queue.push(makeCompleteRoute(s, e));
} else {
e.setParent(start);
queue.push(e);
}
}
if(peak( R ) < peak( S )) {
queue = R
} else {
queue = S
}
}
Отличная статья, по поводу алгоритма «квад дерево» место этого можно использовать алгоритм: «R_tree», пример реализация на java github.com/davidmoten/rtree чтобы проиндексировать точки. Да стратегия вставки в R -tree с {\ displaystyle {\ mathcal {O}} (M \ log M)} {\ mathcal {O}} (M \ log M) более сложной, чем линейная стратегия разделения ( {\ displaystyle {\ mathcal {O}} (M)} {\ mathcal {O}} (M)) R-дерева, но менее сложной, чем квадратичная стратегия разделения ( {\ displaystyle {\ mathcal {O}} (M ^ {2})} {\ mathcal {O}} (M ^ {2})) для размера страницы {\ displaystyle M} Mобъектов и мало влияет на общую сложность.
Сейчас тоже занят задачами на графах и интересно посмотреть как другие работают с этим.
Библиотека быстрого поиска путей на графе