В практиктических приложениях ТАУ часто необходимо точно и качественно идентифицировать объект управления. В этой статье речь пойдет об идентификации объекта управления частотным методом. Данный метод применим, когда есть возможность физически протестировать объект управления синусоидальным входным воздействиямем, изменяя частоту в широком диапазоне. Если это условие соблюдено, то результат, как правило, оправдывает самые оптимистичные ожидания.
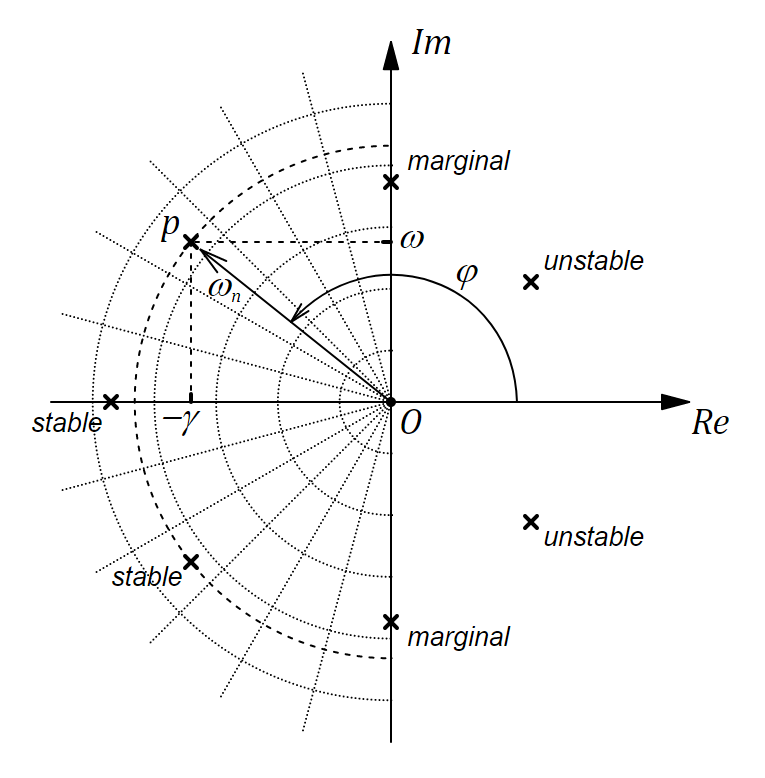
Начнем с краткой теоретической справки. Для понимания материала статьи читателю необходимо иметь представление о следущих вещах:
Как известно, отклик динамической системы на синусоидальное воздействие — есть синусоида с той же частотой, но отличной амплитудой и фазой. Именно эти две характеристики: амплитуда и фаза образуют график Боде, то есть ЛАЧХ и ЛФЧХ. По сути, задача идентификации динамической системы сводится к экспериментальному нахождению этих двух графиков.
Для примера рассмотрим уравнение гармонического осциллятора с ненулевой правой частью как образец линейной динамической системы второго порядка
Обозначим преобразование Лапласа произвольной функции через
через  . Применим преобразование Лапласа к обеим частям уравнения
. Применим преобразование Лапласа к обеим частям уравнения
Тогда характеристическое уравнение динамической системы будет
А передаточная функция
Искомые характеристики ЛАЧХ и ЛФЧХ получаются заменой и взятием модуля и аргумента функции
и взятием модуля и аргумента функции  соответственно
соответственно
Здесь — амплитуда (Magnitude), а
— амплитуда (Magnitude), а  — фаза (Phase) соответствующей компоненты на частоте
— фаза (Phase) соответствующей компоненты на частоте  . В результате получится нечто похожее на это
. В результате получится нечто похожее на это

Характеристика Боде: ЛАЧХ и ЛФЧХ
Эти два графика однозначным образом характеризуют динамическую систему. Справедливо и обратное, зная ЛАЧХ и ЛФЧХ динамической системы с некоторой точностью, можно полностью идентифицировать данную систему в некоторых доверительных интервалах. Вопрос состоит в том, как получить частотные характеристики. Об этом мы и расскажем далее.
Подавая синусоидальное воздействие на вход, мы будем наблюдать примерно такую картину

Синусоидальное входное воздействие и отклик системы
График получен в эксперименте. Как видно из графика, в выходном сигнале явно присутствует синусоидальная составляющая с той же частотой, что и у входного сигнала. Однако, помимо этого там могут содержаться также и высшие гармоники, и шумы. Но не стоит беспокоиться, потому что преобразование Фурье — мощнейший аналитический инструмент, который настолько хорош, что может выделить полезный сигнал, исключая все возмущения.
Допустим, мы измерили два графика, входное воздействие и отклик системы
и отклик системы  , для какой-то заданной частоты входного воздействия
, для какой-то заданной частоты входного воздействия  . Необходимо, чтобы оба измерения были сделаны синхронно и с одинаковым периодом дискретизации
. Необходимо, чтобы оба измерения были сделаны синхронно и с одинаковым периодом дискретизации  , который должен быть известен достаточно точно. Таким образом, мы имеем два набора дискретных значений
, который должен быть известен достаточно точно. Таким образом, мы имеем два набора дискретных значений  и
и  , где
, где  , а
, а  и
и  — значения
— значения  и
и  в соответствующие дискретные моменты времени
в соответствующие дискретные моменты времени  . Следует заметить, что полное время измерения должно быть достаточно большим, чтобы захватить хотя бы несколько (я бы рекомендовал 3 или больше) периодов колебаний.
. Следует заметить, что полное время измерения должно быть достаточно большим, чтобы захватить хотя бы несколько (я бы рекомендовал 3 или больше) периодов колебаний.
К дискретным наборам и
и  можем применить дискретное преобразование Фурье. Дискретное преобразование Фурье переводит вышеуказанные сигналы из временной области в частотную, то есть
можем применить дискретное преобразование Фурье. Дискретное преобразование Фурье переводит вышеуказанные сигналы из временной области в частотную, то есть
где , а
, а  и
и  — соответствующие комплексные амплитуды
— соответствующие комплексные амплитуды  -й гармоники.
-й гармоники.
Теперь применим дискретное преобразование Фурье к нашим двум сигналам. На рисунке ниже показаны графики амплитуд и
и 
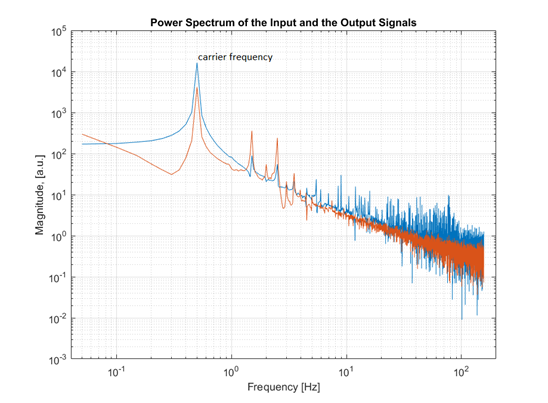
Амплитудный спектр входного и выходного сигнала
График также получен при обработке экспериментальных данных. Как можно видеть, на графике выделяется острый пик на частоте Hz. Это «несущая» частота входного воздействия, то есть частота, на которой происходило возбуждение объекта управления. На обоих графиках, входном и выходном, для данной гармоники наблюдается пик. Из двух значений комплексных амплитуд
Hz. Это «несущая» частота входного воздействия, то есть частота, на которой происходило возбуждение объекта управления. На обоих графиках, входном и выходном, для данной гармоники наблюдается пик. Из двух значений комплексных амплитуд  и
и  на данной частоте получим значение передаточной функции
на данной частоте получим значение передаточной функции  .
.
Как мы помним,
В случае же дискретных и
и  имеем
имеем
Тогда, на графики ЛАЧХ и ЛФЧХ можем нанести точку:
Какую же частоту имеет гармоника с номером ? Отвечаем: частота гармоники дается формулой
? Отвечаем: частота гармоники дается формулой
Можно также записать
Выражение же для, собственно, гармоники следующее
Описанную выше процедуру нужно повторить достаточное количество раз, чтобы захватить весь диапазон частот. Как правило, можно использовать более крупный шаг по частоте в области низких и высоких частот. И наоборот, более мелкий шаг необходим в области промежуточных частот, и особенно вблизи резонансов.
Проделав такой эксперимент и обработав данные, получаем таблицу частотных характеристик
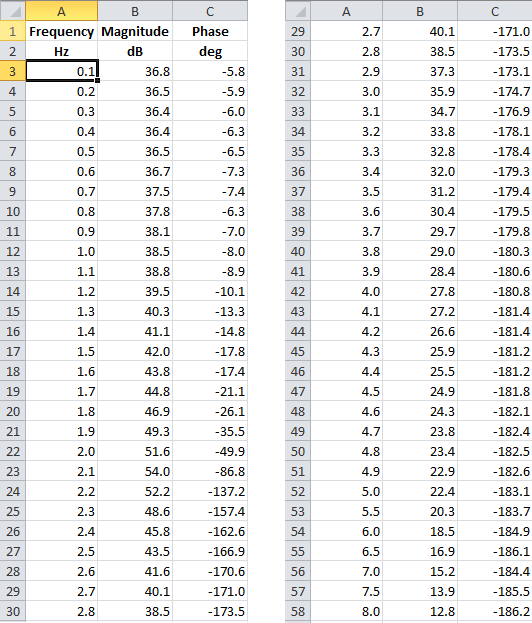
Можно сразу построить измеренные графики ЛАЧХ и ЛФЧХ. Выглядит это примерно вот так
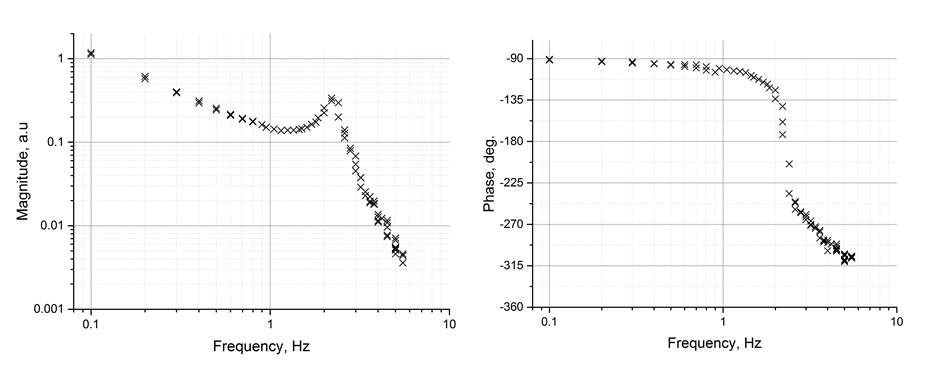
ЛАЧХ и ЛФЧХ, построенные по экспериментальным данным
Нужно сказать, что, хотя мы и пользовались дискретными методами, эти два графика отражают динамику исходной физической системы, то есть объекта управления, без каких-либо упрощений, связанных с дискретизацией (разумеется, в данном диапазоне частот).
Теперь нужно воспользоваться MATLAB, а конкретнее System Identification Toolbox. В составе этого Toolbox'а есть System Identification App — интерактивное приложение, которое может идентифицировать вашу систему по частотным данным. К слову, есть и другие опции, как то, идентификация напрямую по временным измерениям.
Для корректной идентификации необходимо знать порядок системы. Здесь нам поможет график ЛФЧХ. Чтобы узнать порядок системы, посмотрите на график ЛФЧХ и прикиньте, на сколько раз по 90 градусов отстает фаза на высокой частоте. Количество раз по 90 градусов и будет порядок (знаменателя) вашей системы.
Во время идентификации автоматически генерируется отчет, который может быть очень полезен. Выглядит он вот так
Согласно отчету об идентификации, входные данные удовлетворяются найденной моделью на 92.26%. Имеем следующую передаточную функцию физической системы
Теперь у вас есть объект типа IDTF c именем tf1, с которым можно делать все то же самое, что и с любой другой LTI System в MATLAB. Кроме того объект содержит в себе информацию о неопределенности внутренних параметров, и если мы построим Bode Plot, то на графике можно вызвать отображение доверительных интервалов. В настройках можно указать количество стандартных отклонений.
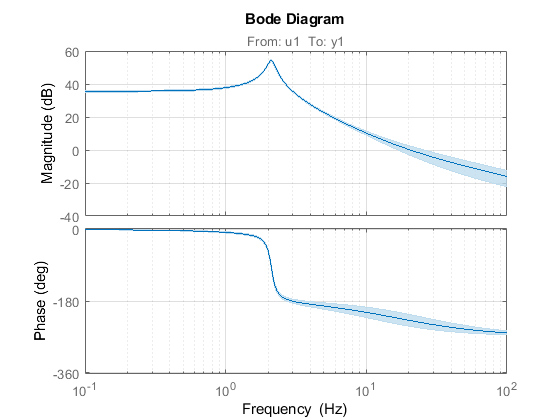
Идентифицированная модель системы с доверительными интервалами
Чтобы проверить правильность идентификации можно совместить экспериментальные точки с графиками частотных характеристик идентифицированной модели
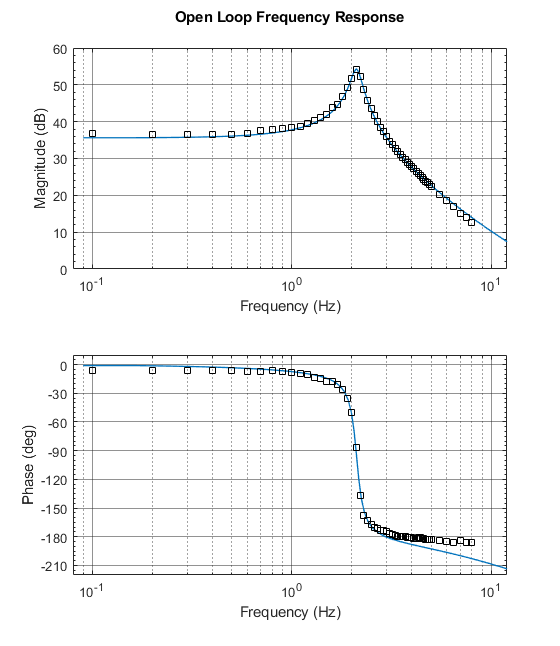
Совмещенные графики для ЛАЧХ и ЛФЧХ
Использование данного метода существенно облегчает процесс проектирования системы управления. Автор статьи успешно разработал и воплотил в железе LQG котроллер для гидравлической цепи специального назначения. Кроме того, данный метод можно использовать для оценки эффективности системы управления, при условии, что вам физически доступно входное воздействие на объект управления со стороны нежелательных возмущений.

Что необходимо знать
Начнем с краткой теоретической справки. Для понимания материала статьи читателю необходимо иметь представление о следущих вещах:
- Преобразование лапласа
- Линейные динамические системы
- Характеристическое уравнение
- Передаточная функция
- Дискретное преобразование Фурье
- Характеристика Боде: ЛАЧХ и ЛФЧХ
Отклик на синусоидальное воздействие
Как известно, отклик динамической системы на синусоидальное воздействие — есть синусоида с той же частотой, но отличной амплитудой и фазой. Именно эти две характеристики: амплитуда и фаза образуют график Боде, то есть ЛАЧХ и ЛФЧХ. По сути, задача идентификации динамической системы сводится к экспериментальному нахождению этих двух графиков.
Для примера рассмотрим уравнение гармонического осциллятора с ненулевой правой частью как образец линейной динамической системы второго порядка
Обозначим преобразование Лапласа произвольной функции
Тогда характеристическое уравнение динамической системы будет
А передаточная функция
Искомые характеристики ЛАЧХ и ЛФЧХ получаются заменой
Здесь

Характеристика Боде: ЛАЧХ и ЛФЧХ
Эти два графика однозначным образом характеризуют динамическую систему. Справедливо и обратное, зная ЛАЧХ и ЛФЧХ динамической системы с некоторой точностью, можно полностью идентифицировать данную систему в некоторых доверительных интервалах. Вопрос состоит в том, как получить частотные характеристики. Об этом мы и расскажем далее.
Подавая синусоидальное воздействие на вход, мы будем наблюдать примерно такую картину

Синусоидальное входное воздействие и отклик системы
График получен в эксперименте. Как видно из графика, в выходном сигнале явно присутствует синусоидальная составляющая с той же частотой, что и у входного сигнала. Однако, помимо этого там могут содержаться также и высшие гармоники, и шумы. Но не стоит беспокоиться, потому что преобразование Фурье — мощнейший аналитический инструмент, который настолько хорош, что может выделить полезный сигнал, исключая все возмущения.
Дискретное преобразование Фурье
Допустим, мы измерили два графика, входное воздействие
К дискретным наборам
где
Применение метода
Теперь применим дискретное преобразование Фурье к нашим двум сигналам. На рисунке ниже показаны графики амплитуд

Амплитудный спектр входного и выходного сигнала
График также получен при обработке экспериментальных данных. Как можно видеть, на графике выделяется острый пик на частоте
Как мы помним,
В случае же дискретных
Тогда, на графики ЛАЧХ и ЛФЧХ можем нанести точку:
Какую же частоту имеет гармоника с номером
Можно также записать
Выражение же для, собственно, гармоники следующее
Описанную выше процедуру нужно повторить достаточное количество раз, чтобы захватить весь диапазон частот. Как правило, можно использовать более крупный шаг по частоте в области низких и высоких частот. И наоборот, более мелкий шаг необходим в области промежуточных частот, и особенно вблизи резонансов.
Проделав такой эксперимент и обработав данные, получаем таблицу частотных характеристик

Можно сразу построить измеренные графики ЛАЧХ и ЛФЧХ. Выглядит это примерно вот так

ЛАЧХ и ЛФЧХ, построенные по экспериментальным данным
Нужно сказать, что, хотя мы и пользовались дискретными методами, эти два графика отражают динамику исходной физической системы, то есть объекта управления, без каких-либо упрощений, связанных с дискретизацией (разумеется, в данном диапазоне частот).
Теперь нужно воспользоваться MATLAB, а конкретнее System Identification Toolbox. В составе этого Toolbox'а есть System Identification App — интерактивное приложение, которое может идентифицировать вашу систему по частотным данным. К слову, есть и другие опции, как то, идентификация напрямую по временным измерениям.
Для корректной идентификации необходимо знать порядок системы. Здесь нам поможет график ЛФЧХ. Чтобы узнать порядок системы, посмотрите на график ЛФЧХ и прикиньте, на сколько раз по 90 градусов отстает фаза на высокой частоте. Количество раз по 90 градусов и будет порядок (знаменателя) вашей системы.
Во время идентификации автоматически генерируется отчет, который может быть очень полезен. Выглядит он вот так
tf1 =
From input "u1" to output "y1":
-97.64 s + 1.063e04
---------------------
s^2 + 1.547 s + 176.7
Name: tf1
Continuous-time identified transfer function.
Parameterization:
Number of poles: 2 Number of zeros: 1
Number of free coefficients: 4
Use "tfdata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using TFEST on frequency response data "h".
Fit to estimation data: 92.26% (stability enforced)
FPE: 120.6, MSE: 112.3
Согласно отчету об идентификации, входные данные удовлетворяются найденной моделью на 92.26%. Имеем следующую передаточную функцию физической системы
Теперь у вас есть объект типа IDTF c именем tf1, с которым можно делать все то же самое, что и с любой другой LTI System в MATLAB. Кроме того объект содержит в себе информацию о неопределенности внутренних параметров, и если мы построим Bode Plot, то на графике можно вызвать отображение доверительных интервалов. В настройках можно указать количество стандартных отклонений.

Идентифицированная модель системы с доверительными интервалами
Чтобы проверить правильность идентификации можно совместить экспериментальные точки с графиками частотных характеристик идентифицированной модели

Совмещенные графики для ЛАЧХ и ЛФЧХ
Заключение
Использование данного метода существенно облегчает процесс проектирования системы управления. Автор статьи успешно разработал и воплотил в железе LQG котроллер для гидравлической цепи специального назначения. Кроме того, данный метод можно использовать для оценки эффективности системы управления, при условии, что вам физически доступно входное воздействие на объект управления со стороны нежелательных возмущений.