
Данная статья является ответом на вот эту статью (Анализ результатов президентских выборов 2018 года. На федеральном и региональном уровне).
В той статье меня удивила фраза автора:
Вместо нормального или логнормального распределения мы видим интересную кривую, с очень странными пиками на круглых значениях (70%, 75%, 80% и т.д.), возрастающую на около-100% явке и уходящей далеко вверх на 100%.Сразу возникают вопросы:
- Почему автор считает, что вместо «странных» пиков должно быть нормальное или логнормальное распределение?
- Почему вообще пики считаются «странными»?
- Откуда могут появиться «естественные» пики на круглых значениях?
Та статья сильно политизирована и комментарии в ней соответствующие. В этой статье мы будем обсуждать только математику, поэтому политические взгляды попрошу держать при себе.
А в качестве бонуса, в конце статьи будет выложен ключ к решению загадки «круглых чисел» на графике выборов 2018.
Исходные данные
Файл БД (MongoDB) с результатами голосования (парсинг с гос. сайта), который был выложен автором исходной статьи:
Файл = 15-04-18.tar.xz
MD5 = 3a1c198cbc4ce102fbc074752fc0ca99
Мы будем исследовать график зависимости процента явки и количества УИКов с данной явкой. В исходной статье он выглядит так:

Вступление
Все желающие могут скачать БД и самостоятельно проверить на наличие ошибок. Мной из полученной БД были случайным образом выбраны и проверены данные по нескольким УИКам, что позволяет с некоторой вероятностью утверждать, что данные были загружены с гос. сайта корректно.
Но, есть некоторые замечания:
Автор исходной статьи пока не дал пояснений, по заданным вопросам:
где results_0 – это «Число избирателей, включенных в список избирателей».
На станицах гос. сайта атрибутов number_bulletin и share нет.
Странность заключается в том, что в БД number_bulletin не всегда считается корректно (с точки зрения официального расчета кол-ва людей принявших участие в выборах).
А именно, официальная формула такая:
В БД number_bulletin в большинстве случае совпадает с этой формулой, но при этом есть и множество УИКов, где number_bulletin отличается, от приведенной выше формулы на кол-во 1-2 и больше бюллетеней, причем закономерности я не увидел.
Вот выборка с примером и hash-ключами УИКов, чтоб можно было быстро найти в БД:
Порядок атрибутов в строке:
ID — ключ УИК
RESULTS_0 – поле results.0 из БД («Число избирателей, включенных в список избирателей»)
TEST_NUMBER_BULLETIN – рассчитанное значение по формуле
RESULTS_NUMBER_BULLETIN — значение в БД
TEST_YAVKA — рассчитанное значение по формуле
RESULTS_SHARE — значение в БД
Таким образом, если обсуждаемый график строился автором из БД с использованием значения share – то этот график не соответствует официальному варианту расчета явки. Но, я допускаю возможность, что данные атрибуты использовались автором в тестовых целях и приведенный им график построен без использования текущих значений share из БД.
В любом случае, все графики данной статьи строятся по официальным формулам и не используют вышеописанные атрибуты.
1. По какой формуле вы считали % явки на каждом уике?Но, по структуре БД видно, что скорее всего, атрибут number_bulletin является самостоятельно рассчитанным параметром определяющим кол-во избирателей включаемых в «явку», а share – это процент явки, рассчитанный по формуле
2. Поясните пожалуйста назначение атрибутов share и number_bulletin.
3. Каким образом округлялись значения до 0.1%?
share = number_bulletin / results_0;где results_0 – это «Число избирателей, включенных в список избирателей».
На станицах гос. сайта атрибутов number_bulletin и share нет.
Странность заключается в том, что в БД number_bulletin не всегда считается корректно (с точки зрения официального расчета кол-ва людей принявших участие в выборах).
А именно, официальная формула такая:
- Число бюллетеней, выданных на участке +
- Число бюллетеней, выданных вне участка +
- Число бюллетеней, выданных досрочно
В БД number_bulletin в большинстве случае совпадает с этой формулой, но при этом есть и множество УИКов, где number_bulletin отличается, от приведенной выше формулы на кол-во 1-2 и больше бюллетеней, причем закономерности я не увидел.
Вот выборка с примером и hash-ключами УИКов, чтоб можно было быстро найти в БД:
Порядок атрибутов в строке:
ID — ключ УИК
RESULTS_0 – поле results.0 из БД («Число избирателей, включенных в список избирателей»)
TEST_NUMBER_BULLETIN – рассчитанное значение по формуле
RESULTS_NUMBER_BULLETIN — значение в БД
TEST_YAVKA — рассчитанное значение по формуле
RESULTS_SHARE — значение в БД
5ab557a2866a6a69f2cf8c90 2241 1368 1367 0,610441 61
5ab557aa866a6a69f2cf8ca8 2853 1665 1662 0,583596 58,25
5ab557b1866a6a69f2cf8cba 2138 1413 1412 0,660898 66,04
5ab557b1866a6a69f2cf8cbb 2093 1291 1290 0,616817 61,63
5ab557b3866a6a69f2cf8cc2 2463 1688 1687 0,685343 68,49
5ab557b5866a6a69f2cf8cc7 1583 1085 1084 0,685407 68,48
5ab557b9866a6a69f2cf8cd7 1483 912 911 0,614969 61,43
5ab557ba866a6a69f2cf8cdb 2166 1403 1402 0,647737 64,73
5ab557bb866a6a69f2cf8cdd 2186 1204 1203 0,550777 55,03
5ab557bc866a6a69f2cf8ce1 1574 986 985 0,626429 62,58
5ab557bd866a6a69f2cf8ce5 1284 803 802 0,625389 62,46
5ab557bd866a6a69f2cf8ce6 2543 1610 1608 0,63311 63,23
5ab557bf866a6a69f2cf8ced 2215 1353 1350 0,610835 60,95
5ab557cf866a6a69f2cf8d36 1627 1374 1372 0,844499 84,33
5ab557f7866a6a69f2cf8dbd 449 262 261 0,583518 58,13
5ab557f8866a6a69f2cf8dbf 597 349 347 0,584589 58,12
5ab55809866a6a69f2cf8dfa 194 156 155 0,804123 79,9Таким образом, если обсуждаемый график строился автором из БД с использованием значения share – то этот график не соответствует официальному варианту расчета явки. Но, я допускаю возможность, что данные атрибуты использовались автором в тестовых целях и приведенный им график построен без использования текущих значений share из БД.
В любом случае, все графики данной статьи строятся по официальным формулам и не используют вышеописанные атрибуты.
Официальная формула расчета явки:
- Число бюллетеней, выданных на участке +
- Число бюллетеней, выданных вне участка +
- Число бюллетеней, выданных досрочно
Все графики в данной статье построены по следующим параметрам:
Явка на каждом уике = формула приведенная выше
Округление до ближайшего целого:
10.2 => 10
10.5 => 11
Округление до первого знака после запятой и последующих..:
0.22 => 0.2
0.25 => 0.3
Визуализация #1
Давайте посмотрим на графики с визуализацией кол-ва УИК по проценту явки, дополнительно добавив линию со средним размером УИК, чтобы проверить возможную корреляцию:
График_1а:
Ось Х – Процент явки (интервал = 1%)
Ось Y(левая) – Количество УИК
Ось Y(правая) – Средний размер одного УИК (кол-во зарег. избирателей)
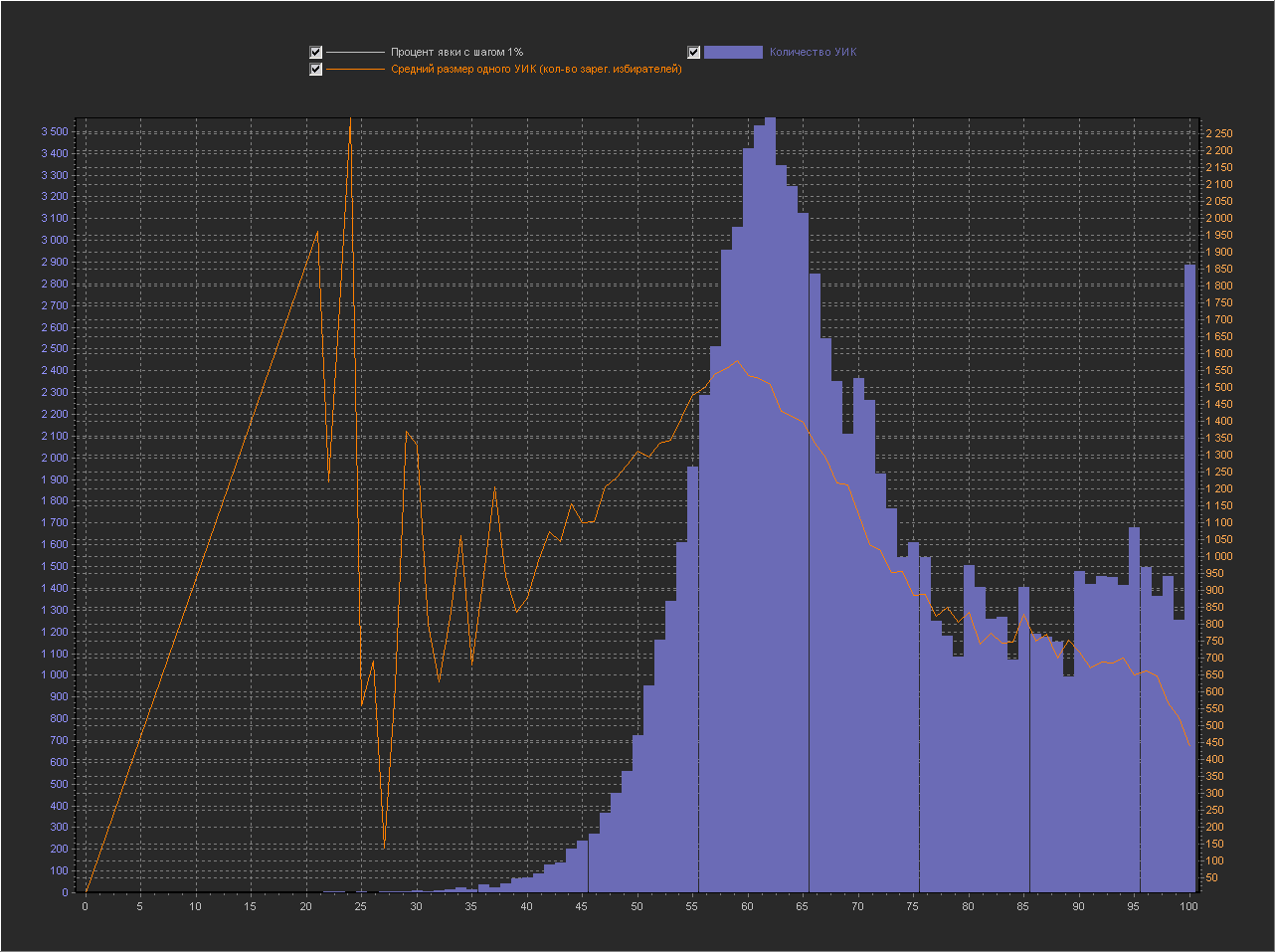
Видно, что на точке X=100 значение очень высокое, а средний размер УИК при этом уменьшается. В обсуждении fediq высказывалось логичное предположение:
Высокая явка — нормальное явление для высокоорганизованных УИКов типа традиционных общин, режимных учреждений, военных частей.Давайте посмотрим на первые 10 регионов по кол-ву УИК со 100% явкой:
K_ALL — кол-во УИК в регионе
K_100 — кол-во УИК со 100% явкой
REGION — название региона
K_ALL K_100 REGION
393 346 foreign-countries
1580 213 primorsk
1911 165 dagestan
482 156 sakhalin
596 138 murmansk
2817 132 tatarstan
2052 128 st-petersburg
317 123 kamchatka_krai
948 67 arkhangelsk
854 60 khabarovskГрафик_1б:
Ось Х – Процент явки (интервал = 0.1%)
Ось Y(левая) – Количество УИК
Ось Y(правая) – Средний размер одного УИК (кол-во зарег. избирателей)
+ Не выводится точка 100%, т.к. с ней остальные значения слишком мелкие.

Появились те самые пики на круглых значениях.
График_1в:
Ось Х – Процент явки (интервал = 0.01%)
Ось Y(левая) – Количество УИК
+ Не выводится точка 100%, т.к. с ней остальные значения слишком мелкие.

Как и ожидалось с уменьшением шага кол-во пиков увеличивается и они расположены по всему графику.
График_1г:
Ось Х – Процент явки (интервал = 0.001%)
Ось Y(левая) – Количество УИК
+ Не выводится точка 100%, т.к. с ней остальные значения слишком мелкие.

Как мы видим весь график в пиках, т.е. на данном масштабе – пики это нормальное явление.
График_1д:
Ось Х – Процент явки (интервал = 0.001%)
Ось Y(левая) – Количество УИК
Увеличенная область для значения 80%

Видим, что рядом с круглым 80% много мелких значений.
Визуализация #2
Теперь давайте посмотрим на те же самые графики, но под другим углом. Так как расположенные рядом друг с другом на графике по оси X точки (процент явки) ни чем не связаны (в каждую такую точку-выборку попадают совершенно разные УИКи с различным гео-положением, размером и настроением избирателей и т.п...), то разницы в каком порядке они стоят нет, поэтому отсортируем их по оси Х не по возрастанию процента явки, а по возрастанию кол-ва УИКов.
Т.е. на графиках выше мы видели, как при возрастании процента явки ведет себя кол-во УИК, а на данном графике мы увидим, как при возрастании кол-ва УИК ведет себя процент явки.
График_2а:
Ось Х – номер точки из БД по порядку
Ось Y(левая) – Количество УИК
Ось Y(правая) – Процент явки (интервал = 1%)

Это тот же самый график, который приведен выше, но ось X (белый цвет) теперь перенесена на Ось Y(правая) и отображается в виде отдельной линии, Ось Y(левая) так же как и раньше отображает кол-во УИК, а на оси X теперь отображается просто номер выборки из БД (номер точки по оси X по порядку).
Пояснение
Точке по оси X с номером 60 соответствует:
процент явки = 95
кол-во УИК = 1680
График_2б:
Ось Х – номер точки из БД по порядку
Ось Y(левая) – Количество УИК
Ось Y(правая) – Процент явки (интервал = 0.1%)
+ Не выводится точка 100%, т.к. с ней остальные значения слишком мелкие.
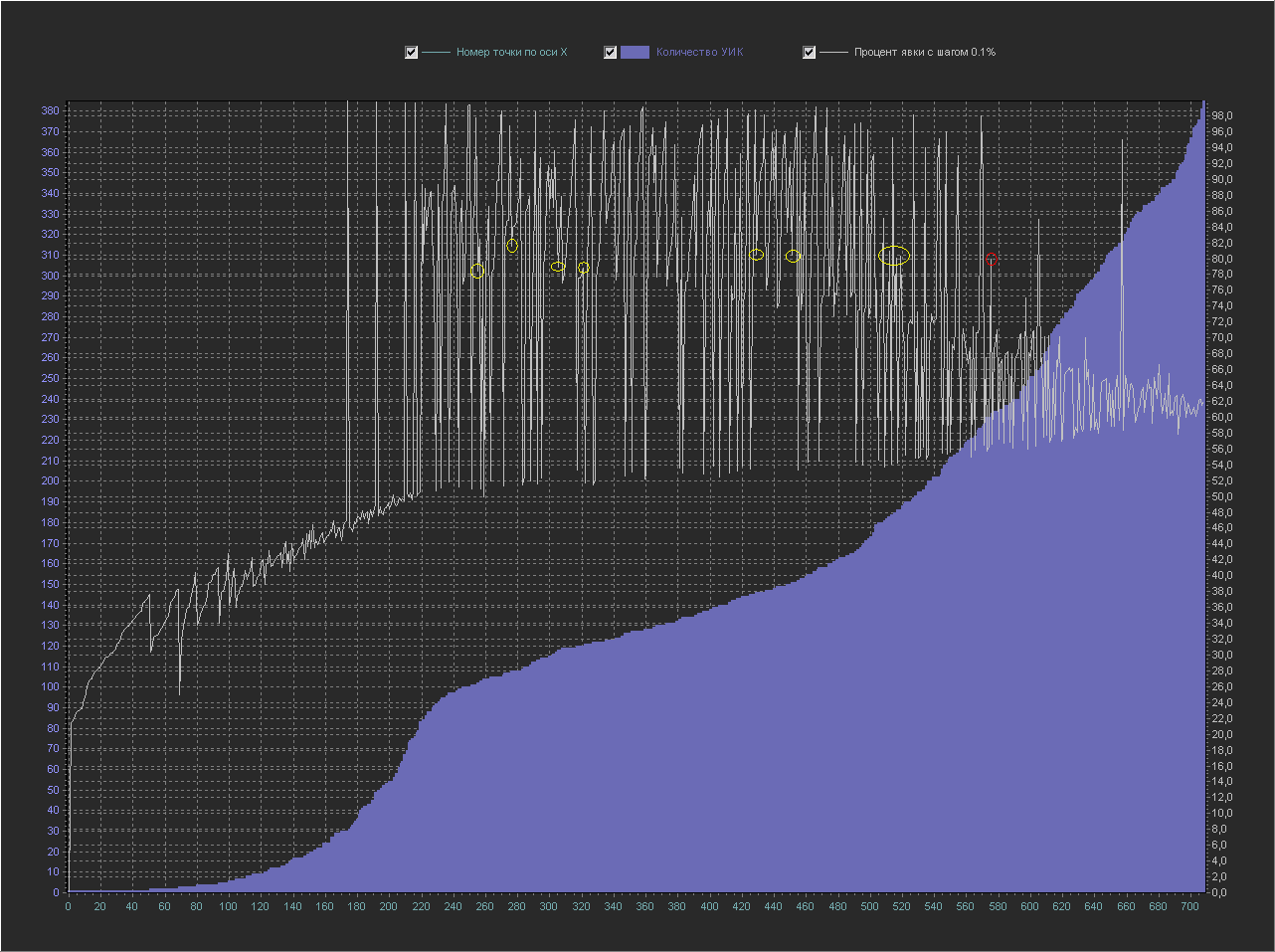
Давайте найдем на этом графике нашу круглую точку 80% (обведена красным кружком), которая на графике выше выглядела как пика с мелкими значениями вокруг себя.
Здесь она уже выглядит менее вычурно на линии с точками близкими ей по значению процента явки (желтые кружки).
График_2в:
Ось Х – номер точки из БД по порядку
Ось Y(левая) – Количество УИК
Ось Y(правая) – Процент явки (интервал = 0.01%)
+ Не выводится точка 100%, т.к. с ней остальные значения слишком мелкие.
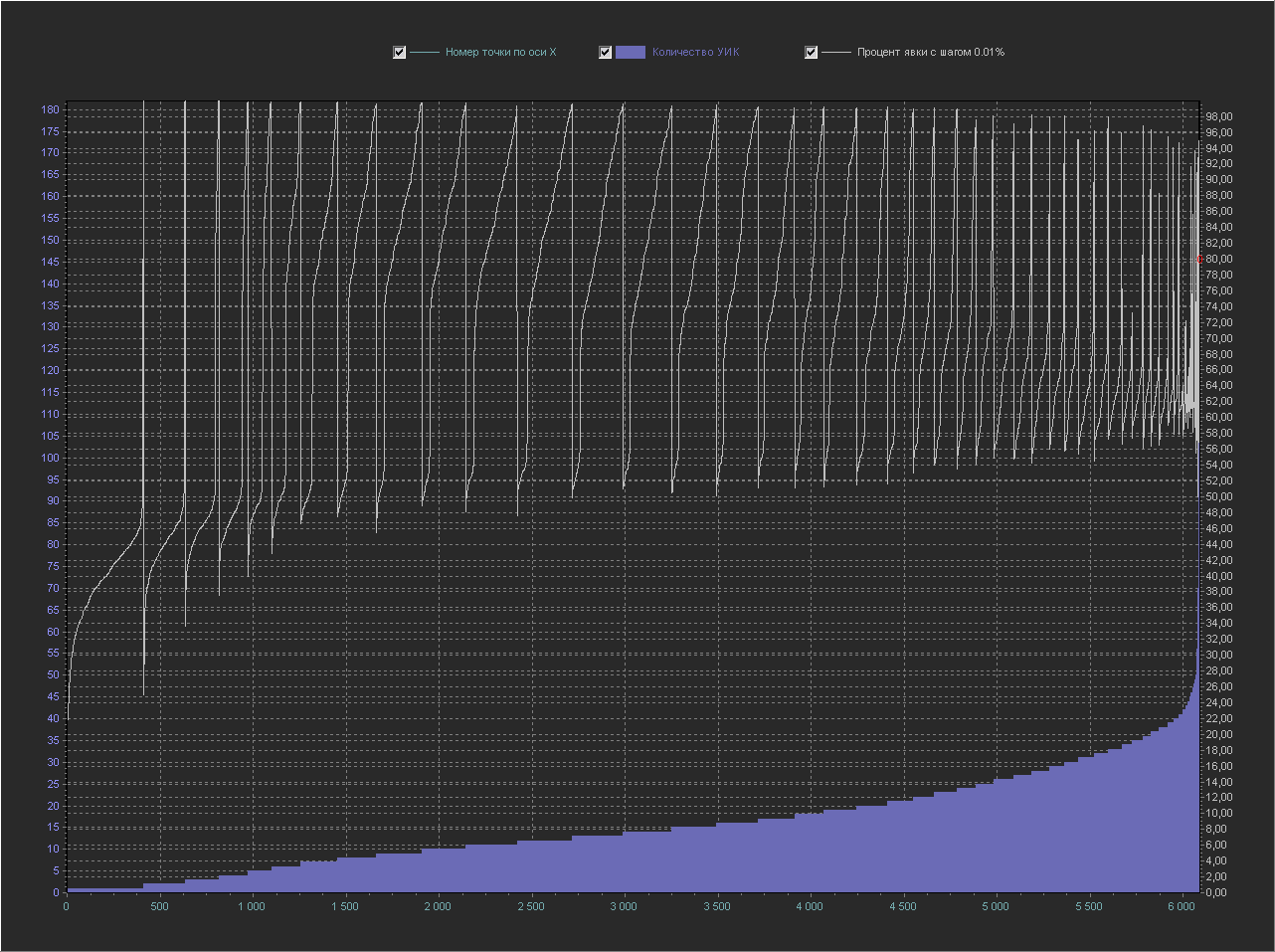
А вот это уже интересно, те, кто разбирается в математике уже наверно начинают понимать в чем фишка. А точку 80% уже не различить, т.к. на этом масштабе она уже не видна.
График_2г:
Ось Х – номер точки из БД по порядку
Ось Y(левая) – Количество УИК
Ось Y(правая) – Процент явки (интервал = 0.001%)
+ Не выводится точка 100%, т.к. с ней остальные значения слишком мелкие.

А этот график – просто откровение. Можно даже посчитать кол-во ступенек в каждом периоде…
Ключ к решению загадки круглых чисел
Ну и в качестве бонуса, любителям «конспиралогии» и математических ребусов посвящается:
PROCENTX KOLVO X2 X5 X10
25 2 2 0 0
40 5 2 5 2
45 3 3 3 3
50 70 70 15 15
55 10 10 10 10
60 108 57 108 57
65 34 34 34 34
70 57 57 57 57
75 140 140 29 29
80 122 62 122 62
85 36 36 36 36
90 78 78 78 78
95 64 64 64 64
100 2613 1370 582 324Это красивая закономерность, которую я обнаружил в «круглых цифрах».
Суть в том, что начиная с точки 40% и далее с шагом 5% количество зарегистрированных избирателей в УИК всегда кратно 2, 5 или 10. Собственно таблица выше это отображает.
PROCENTX – процент явки
KOLVO – общее кол-во УИК ровно с данным процентом без каких-либо округлений
X2 – количество УИК в которых кол-во зарег. избирателей кратно 2
X5 – количество УИК в которых кол-во зарег. избирателей кратно 5
X10 – количество УИК в которых кол-во зарег. избирателей кратно 10
Далее, я решил проверить кратность с шагом 1…
PROCENTX KOLVO X2 X5 X10
25 2 2 0 0
34 1 1 1 1
36 1 1 1 1
40 5 2 5 2
42 1 1 1 1
44 2 0 2 0
45 3 3 3 3
46 1 1 1 1
47 1 1 1 1
48 2 0 2 0
50 70 70 15 15
51 3 3 3 3
52 7 4 7 4
53 4 4 4 4
54 4 4 4 4
55 10 10 10 10
56 10 6 10 6
57 5 5 5 5
58 9 9 9 9
59 4 4 4 4
60 108 57 108 57
61 3 3 3 3
62 18 18 18 18
63 1 1 1 1
64 23 10 23 10
65 34 34 34 34
66 14 14 14 14
67 8 8 8 8
68 22 10 22 10
69 2 2 2 2
70 57 57 57 57
71 4 4 4 4
72 17 5 17 5
73 6 6 6 6
74 8 8 8 8
75 140 140 29 29
76 23 11 23 11
77 4 4 4 4
78 10 10 10 10
79 2 2 2 2
80 122 62 122 62
81 10 10 10 10
82 14 14 14 14
83 6 6 6 6
84 24 11 24 11
85 36 36 36 36
86 10 10 10 10
87 3 3 3 3
88 23 8 23 8
89 4 4 4 4
90 78 78 78 78
91 4 4 4 4
92 31 17 31 17
93 6 6 6 6
94 13 13 13 13
95 64 64 64 64
96 25 11 25 11
97 6 6 6 6
98 17 17 17 17
99 4 4 4 4
100 2613 1370 582 324
Получается, что такая закономерность соблюдается кроме 100 на всех целых числах (в которых имеется ровно целое значение, если целого значения нет – оно в списке пропущено).
Ну и напоследок, общее разбиение по кратности количества зарегистрированных избирателей x2-10 для всех УИК:
KOLVO X2 X3 X4 X5 X6 X7 X8 X9 X10
97699 49413 32753 24724 20283 16649 13923 12464 10917 10411 KOLVO – общее кол-во УИК в которых проводились выборы
X2-10 – количество УИК в которых кол-во зарег. избирателей кратно 2-10
И общее разбиение по кратности пришедших на выборы избирателей x2-10 для всех УИК:
KOLVO X2 X3 X4 X5 X6 X7 X8 X9 X10
97699 49268 32712 24634 20608 16492 14085 12192 10938 10752KOLVO – общее кол-во УИК в которых проводились выборы
X2-10 – количество УИК в которых кол-во пришедших избирателей кратно 2-10
Ну, а дальше обычно в таких случаях математики пишут… решение тривиально :)
Update:
Заключение
Как ни странно, но моя статья оказалась довольно двусмысленна для тех, кто присоединился к обсуждению без чтения основной статьи на которую делался ответ и дискуссии, которая там велась. Поэтому добавлю здесь пояснения, в виде ответов на поставленные мной вопросы в начале статьи.
Почему автор (исходной статьи) считает, что вместо «странных» пиков должно быть нормальное или логнормальное распределение?
— Ответа я так и не получил.
Но, мое мнение такое — ожидать что, на графике голосования (где участвует разумный выбор) должно быть обязательно нормальное или логнормальное распределение — не верно.
Почему вообще пики считаются «странными»?
— В исходной статье на это была версия «Зато это можно объяснить тем, что при фальсификации председатели предпочитали комиссий брать «круглые» цифры процентов.», а так же «Потому, что я не вижу естественных причин их появления на круглых числах.»
Откуда могут появиться «естественные» пики на круглых значениях?
— Это уже был мой вопрос самому себе, для решения которого я просил автора исходной статьи выложить файл БД для возможности анализа.
Собственно эта статья на него и отвечает — по графикам График_1в, График_1г мы видим — что наличие пиков на обсуждаемом графике — вполне естественно, а причина их появления кроется в дроби
количество_избирателей_пришедших_на_выборы / количество_избирателей_зарегистрированных_на_участке
Значение которой имеет более высокую вероятность оказаться «круглым» чем другие, это подтверждается данными из раздела «Ключ к решению загадки круглых чисел». Но надо иметь в виду, что под «круглыми» значениями здесь понимаются «ровно круглые» значения без какого либо округления, т.е. иллюстрируемые пики на График_1г и График_1в. На График_1б — значения уже сильно округлены и к «ровно круглым» значениям, добавляются значения из ближайших окрестностей, поэтому «естественность» пик на «ровно круглых» значениях оказывает уже гораздо меньше влияния чем «разумный выбор». Поэтому появление высоких пик на круглых значениях в реальном голосовании, показанная нами «естественность» не объясняет. Но, то что они существуют и могут быть усилены «разумным выбором» вполне вероятно.
Дополнительные пояснения
Вся статья задумывалась как некая загадка, которую можно решить если использовать логику и минимум математических знаний. Само решение, благодаря подсказкам в виде графиков и данных «ключа», на мой взгляд, казалось настолько очевидным, что большинству читателей потребуется минимум усилий, чтобы понять о чем речь. Но, теперь ясно, что это не так, и как говорится телепатов нет, и эта «загадочность» больше путает, чем помогает понять смысл статьи.
Вот дополнительные пояснения (я буду нумеровать тезисы, чтобы можно было на них ссылаться в случае несогласия):
Графики 2абвг строились для визуализации моей мысли о том, что три точки стоящие рядом друг с другом по порядку на графиках 1абвг — между собой никак не связаны.
Т.е. например 79,80,81 — включают в себя совершенно разные по параметрам УИКи (размер, гео-расположение, разумность избирателей) и никакой прямой связи между этими точками нет, т.е. допустим пика на 80 относительно 79 и 81 пикой является только в силу того, что на числовой прямой эти числа стоят рядом и дополнительной смысловой нагрузки не несет. Т.е. нет никакой «обязательности» в том, чтобы изменения значения процента явки между этими точками было всегда ниже некого субъективного порога, выше которого это изменение можно назвать «пикой». Упрощенно – наличие пик на графиках 1бвг, вызывает у некоторых читателей субъективное чувство «не естественности», т.к. они видят, что в других местах график выглядит более гладко, это происходит из-за некоего подсознательного ожидания нормального распределения функции на графике. Но такое ожидание является заблуждением. Для иллюстрации этого заблуждения и были показаны графики 2абвг. Суть этих графиков в том, что отображают они ровно одни и те же данные, что на графиках 1абвг, но кол-во субъективных «аномалий» сильно отличается.
Графики 2абвг отсортированы не по возрастанию процента явки, как 1абвг, а по возрастанию кол-ва УИКов. Естественно, пики по количеству УИКов пропали, они идут по возрастанию, но теперь появилась ломаная кривая (белого цвета), на которой мы и будем искать «пики». Т.е. мы пытаемся найти «аномалии» на другой визуализации одних и тех же данных.
Давайте посмотрим на График_2а (шаг 1%):
В зависимости от субъективного выбора и наших ожиданий на графике, мы можем, как обнаружить здесь «аномалии», так и считать что их нет.
Их нет, если посмотреть по линии 56% или 68% и т.п… то все колебания (нижние, верхние пики рядом с этими линиями) особо не выделяются.
Они есть, если мы будем использовать логику «аномалий» из графика 1абвг, где «аномальность» формулировалась вопросом «Как может быть так, чтобы явка X% была на большом кол-ве УИК, а (X-1)% и (X+1)% на маленьком?», то здесь «аномальность» формулируется вопросом «Почему в точке X – с N кол-вом УИКов высокий процент явки, а в точках (X+1) и (X-1) (в которых N+1 и N-1 не сильно отличаются от N) процент явки гораздо ниже?»
И в наличии и в отсутствии аномалий есть некая логика, давайте посмотрим, куда она нас заведет дальше.
График_2б (шаг 0.1%):
Здесь, если мы считали, что на График_2а – нет аномалий, мы в этом дополнительно убеждаемся. Это показано на примере линии с 80%, если на график_1б 80% — это одинокая пика, то здесь рядом с линией 80% есть еще множество значений близких к 80% (отмечены желтыми кружками).
А вот если мы придерживаемся понятия «аномальности» для графиков 1бвг, то здесь у нас вообще всё в пиках и одна сплошная «аномальность» никаких «гладких» мест на линии белого цвета практически нет.
Таким образом, в зависимости от способа визуализации и выбранного критерия «аномальности», мы можем придти к двум совершенно противоположным выводам.
График_2в (шаг 0.01%):
На этом масштабе интересен тот факт, что по оси X уже выводится достаточно много точек, чтобы увидеть, как изменяется процент явки для УИКов с одинаковым количеством зарегистрированных избирателей. Внутри каждой уже достаточно широкой ступеньки располагается некое распределение явки и это распределение уже можно сравнивать между разными ступеньками. В комментарии к графику я дал намек на то, что любители математики должны явно заметить вид периодической функции и некую «аномалию» из-за того, что в ней меняется ширина периода (согласен, так себе был намек :).
График_2г (шаг 0.001%):
Ну… а здесь я просто откровенно прикололся, показав, что «аномалии» можно буквально создавать из воздуха. На графике – реальные данные, и если проверить значения каждой точки – все честно, при этом мы видим явно «искусственные» ступеньки, которые должны безапелляционно «доказывать», что выборы «нарисованы».
На самом деле секрет прост. На нашем графике сортировка идет по количеству УИКов, и на одной ступеньке (фиолетовый цвет) мы видим множество УИКов, каждому из которых соответствует свой процент явки (на белой линии), так вот, все ступеньки идут по возрастанию, а что происходит внутри ступенек? А внутри ступенек мы можем делать, все что угодно. На предыдущем графике мы внутри ступенек отсортировали УИКи по возрастанию у них процента явки… и получилась, такая изогнутая плавно возрастающая линия. А здесь сортировка внутри ступенек вообще была отключена и они выводились на график в той последовательности, в которой хранятся в БД (бинарное дерево или что-то вроде того), что привило к рисованию таких вот ступенек процента явки (на белой линии).
Ну и собственно мой первый тезис:
Тезис 1:
От выбранного способа визуализации зависит количество некой субъективной «аномальности» на графике. Причем, всё зависит от того, что мы понимаем под «аномальностью». Пики на графике 1бвг – субъективно некоторыми людьми считаются «аномальностью» лишь из-за «геометрической» близости точек с высоким и низким значением (без какого-либо доказательства, что таких пиков на графике быть не должно), замечу еще раз, что кроме «геометрической» близости между этими точками никакой связи нет. Грубо говоря, мы можем сортировать их всё новым, и новым способом находя всё новые и новые «геометрические» аномалии, которые не несут в себе никакой смысловой нагрузки. Вот когда появится доказательство, что пиков на какой-то визуализации быть не должно, а они там есть – вот тогда, такая визуализация имеет смысл.
Теперь пояснения по графикам 1абвг:
Здесь мы разбираем тот вариант, когда за «доказательство» на запрет появления пиков выдается «не знание способа, как эти пики могут появиться естественным путем». Т.е. для некоторых людей, появление пиков на круглых значениях – очень маловероятное событие и кроме как вмешательством «конспиралогических» факторов необъяснимое.
График_1а (шаг 1%):
Это базовый график, на котором нет «аномалий».
График_1б (шаг 0.1%):
Это график, в котором автор исходной статьи обнаружил и показал «аномальные» пики на круглых значениях. И да, действительно, если на этой визуализации следовать логике «геометрической» близости точек и ожидать нормального распределения, то пики – это анамалия.
График_1в (шаг 0.01%):
Здесь мы уменьшаем шаг и уже видим гораздо больше пиков, причем они разбросаны по всему графику. О чем это говорит? Что мы обнаружили еще больше аномалий? Или может для данного графика пики просто сами по себе являются нормальным явлением?
График_1г (шаг 0.001%):
Ну, тут ответ на вопрос выше очевиден – весь график состоит из пик, значит либо весь график – аномалия, либо пики – это нормальное (естественное) явление для данной визуализации, и значит бездоказательно считать, что пики на графике График_1б «аномалия» — это ошибка. Ибо утверждать, что пики маловероятны мы уже не можем.
Тезис 2:
На графиках 1абвг – просто голословное утверждение, что пики «маловероятны» — не является доказательством «аномальности» пиков, так как на График_1а их нет, а на всех последующих График_бвг с уменьшением шага их становится всё больше и больше.
Ну и собственно разгадка пиков на круглых значениях:
По графикам График_1в, График_1г мы видим — что наличие пиков на обсуждаемом графике — вполне естественно, а причина их появления кроется в дроби:
количество_избирателей_пришедших_на_выборы / количество_избирателей_зарегистрированных_на_участке
Значение которой имеет более высокую вероятность оказаться «круглым» чем другие, это подтверждается данными из раздела «Ключ к решению загадки круглых чисел».
Визуально, подсказка на это дается в графике График_1д, где видно пустую воронку вокруг значения 80%.
Входные данные для задачи:
1. По таблице мы видим, что в точки для всех «круглых» значений процента явки – попадают только УИКи в которых кол-во зарег. избирателей кратно 2,5 или 10.
2. Далее приведены таблицы с данными по кратности 2,3,4,5,6,7,8,9,10 для всех УИКов
по кол-ву пришедших на выборы избирателей (числитель)
и
по кол-ву зарег. избирателей (знаменатель)
Ну а дальше, можно посчитать вероятности по появлению интересующих значений, но это я уже оставляю на откуп читателям статьи. Если кому-то нужно, могу привести больше данных по кратности.
Еще просто для справки:
Минимальный размер (кол-во зарег.избирателей) УИКа = 3 чел
Максимальный = 7746 чел
Вот дополнительные пояснения (я буду нумеровать тезисы, чтобы можно было на них ссылаться в случае несогласия):
Графики 2абвг строились для визуализации моей мысли о том, что три точки стоящие рядом друг с другом по порядку на графиках 1абвг — между собой никак не связаны.
Т.е. например 79,80,81 — включают в себя совершенно разные по параметрам УИКи (размер, гео-расположение, разумность избирателей) и никакой прямой связи между этими точками нет, т.е. допустим пика на 80 относительно 79 и 81 пикой является только в силу того, что на числовой прямой эти числа стоят рядом и дополнительной смысловой нагрузки не несет. Т.е. нет никакой «обязательности» в том, чтобы изменения значения процента явки между этими точками было всегда ниже некого субъективного порога, выше которого это изменение можно назвать «пикой». Упрощенно – наличие пик на графиках 1бвг, вызывает у некоторых читателей субъективное чувство «не естественности», т.к. они видят, что в других местах график выглядит более гладко, это происходит из-за некоего подсознательного ожидания нормального распределения функции на графике. Но такое ожидание является заблуждением. Для иллюстрации этого заблуждения и были показаны графики 2абвг. Суть этих графиков в том, что отображают они ровно одни и те же данные, что на графиках 1абвг, но кол-во субъективных «аномалий» сильно отличается.
Графики 2абвг отсортированы не по возрастанию процента явки, как 1абвг, а по возрастанию кол-ва УИКов. Естественно, пики по количеству УИКов пропали, они идут по возрастанию, но теперь появилась ломаная кривая (белого цвета), на которой мы и будем искать «пики». Т.е. мы пытаемся найти «аномалии» на другой визуализации одних и тех же данных.
Давайте посмотрим на График_2а (шаг 1%):
В зависимости от субъективного выбора и наших ожиданий на графике, мы можем, как обнаружить здесь «аномалии», так и считать что их нет.
Их нет, если посмотреть по линии 56% или 68% и т.п… то все колебания (нижние, верхние пики рядом с этими линиями) особо не выделяются.
Они есть, если мы будем использовать логику «аномалий» из графика 1абвг, где «аномальность» формулировалась вопросом «Как может быть так, чтобы явка X% была на большом кол-ве УИК, а (X-1)% и (X+1)% на маленьком?», то здесь «аномальность» формулируется вопросом «Почему в точке X – с N кол-вом УИКов высокий процент явки, а в точках (X+1) и (X-1) (в которых N+1 и N-1 не сильно отличаются от N) процент явки гораздо ниже?»
И в наличии и в отсутствии аномалий есть некая логика, давайте посмотрим, куда она нас заведет дальше.
График_2б (шаг 0.1%):
Здесь, если мы считали, что на График_2а – нет аномалий, мы в этом дополнительно убеждаемся. Это показано на примере линии с 80%, если на график_1б 80% — это одинокая пика, то здесь рядом с линией 80% есть еще множество значений близких к 80% (отмечены желтыми кружками).
А вот если мы придерживаемся понятия «аномальности» для графиков 1бвг, то здесь у нас вообще всё в пиках и одна сплошная «аномальность» никаких «гладких» мест на линии белого цвета практически нет.
Таким образом, в зависимости от способа визуализации и выбранного критерия «аномальности», мы можем придти к двум совершенно противоположным выводам.
График_2в (шаг 0.01%):
На этом масштабе интересен тот факт, что по оси X уже выводится достаточно много точек, чтобы увидеть, как изменяется процент явки для УИКов с одинаковым количеством зарегистрированных избирателей. Внутри каждой уже достаточно широкой ступеньки располагается некое распределение явки и это распределение уже можно сравнивать между разными ступеньками. В комментарии к графику я дал намек на то, что любители математики должны явно заметить вид периодической функции и некую «аномалию» из-за того, что в ней меняется ширина периода (согласен, так себе был намек :).
График_2г (шаг 0.001%):
Ну… а здесь я просто откровенно прикололся, показав, что «аномалии» можно буквально создавать из воздуха. На графике – реальные данные, и если проверить значения каждой точки – все честно, при этом мы видим явно «искусственные» ступеньки, которые должны безапелляционно «доказывать», что выборы «нарисованы».
На самом деле секрет прост. На нашем графике сортировка идет по количеству УИКов, и на одной ступеньке (фиолетовый цвет) мы видим множество УИКов, каждому из которых соответствует свой процент явки (на белой линии), так вот, все ступеньки идут по возрастанию, а что происходит внутри ступенек? А внутри ступенек мы можем делать, все что угодно. На предыдущем графике мы внутри ступенек отсортировали УИКи по возрастанию у них процента явки… и получилась, такая изогнутая плавно возрастающая линия. А здесь сортировка внутри ступенек вообще была отключена и они выводились на график в той последовательности, в которой хранятся в БД (бинарное дерево или что-то вроде того), что привило к рисованию таких вот ступенек процента явки (на белой линии).
Ну и собственно мой первый тезис:
Тезис 1:
От выбранного способа визуализации зависит количество некой субъективной «аномальности» на графике. Причем, всё зависит от того, что мы понимаем под «аномальностью». Пики на графике 1бвг – субъективно некоторыми людьми считаются «аномальностью» лишь из-за «геометрической» близости точек с высоким и низким значением (без какого-либо доказательства, что таких пиков на графике быть не должно), замечу еще раз, что кроме «геометрической» близости между этими точками никакой связи нет. Грубо говоря, мы можем сортировать их всё новым, и новым способом находя всё новые и новые «геометрические» аномалии, которые не несут в себе никакой смысловой нагрузки. Вот когда появится доказательство, что пиков на какой-то визуализации быть не должно, а они там есть – вот тогда, такая визуализация имеет смысл.
Теперь пояснения по графикам 1абвг:
Здесь мы разбираем тот вариант, когда за «доказательство» на запрет появления пиков выдается «не знание способа, как эти пики могут появиться естественным путем». Т.е. для некоторых людей, появление пиков на круглых значениях – очень маловероятное событие и кроме как вмешательством «конспиралогических» факторов необъяснимое.
График_1а (шаг 1%):
Это базовый график, на котором нет «аномалий».
График_1б (шаг 0.1%):
Это график, в котором автор исходной статьи обнаружил и показал «аномальные» пики на круглых значениях. И да, действительно, если на этой визуализации следовать логике «геометрической» близости точек и ожидать нормального распределения, то пики – это анамалия.
График_1в (шаг 0.01%):
Здесь мы уменьшаем шаг и уже видим гораздо больше пиков, причем они разбросаны по всему графику. О чем это говорит? Что мы обнаружили еще больше аномалий? Или может для данного графика пики просто сами по себе являются нормальным явлением?
График_1г (шаг 0.001%):
Ну, тут ответ на вопрос выше очевиден – весь график состоит из пик, значит либо весь график – аномалия, либо пики – это нормальное (естественное) явление для данной визуализации, и значит бездоказательно считать, что пики на графике График_1б «аномалия» — это ошибка. Ибо утверждать, что пики маловероятны мы уже не можем.
Тезис 2:
На графиках 1абвг – просто голословное утверждение, что пики «маловероятны» — не является доказательством «аномальности» пиков, так как на График_1а их нет, а на всех последующих График_бвг с уменьшением шага их становится всё больше и больше.
Ну и собственно разгадка пиков на круглых значениях:
По графикам График_1в, График_1г мы видим — что наличие пиков на обсуждаемом графике — вполне естественно, а причина их появления кроется в дроби:
количество_избирателей_пришедших_на_выборы / количество_избирателей_зарегистрированных_на_участке
Значение которой имеет более высокую вероятность оказаться «круглым» чем другие, это подтверждается данными из раздела «Ключ к решению загадки круглых чисел».
Визуально, подсказка на это дается в графике График_1д, где видно пустую воронку вокруг значения 80%.
Входные данные для задачи:
1. По таблице мы видим, что в точки для всех «круглых» значений процента явки – попадают только УИКи в которых кол-во зарег. избирателей кратно 2,5 или 10.
2. Далее приведены таблицы с данными по кратности 2,3,4,5,6,7,8,9,10 для всех УИКов
по кол-ву пришедших на выборы избирателей (числитель)
и
по кол-ву зарег. избирателей (знаменатель)
Ну а дальше, можно посчитать вероятности по появлению интересующих значений, но это я уже оставляю на откуп читателям статьи. Если кому-то нужно, могу привести больше данных по кратности.
Еще просто для справки:
Минимальный размер (кол-во зарег.избирателей) УИКа = 3 чел
Максимальный = 7746 чел
Update2:
Модель выборов на основе кратности размеров УИКов из раздела 'Ключ'
Я думаю такой модели, которая может симулировать реальный «разумный выбор» всей страны создать невозможно :)
Но, я могу построить модель, которая будет использовать реальные данные по голосованию и мы посмотрим, что получится. В разделе «ключ» изначально были представлены таблицы с данными по кратности, я их выложил с самого начала, так как по моим прикидкам вероятности, которые они описывают, как раз и являются «ключом» к решению проблемы. Но формулы и расчеты это одно, а практика это другое… давайте проверим.
Вот визуализация, основанная на таблице кратности размеров УИК:
Шаг выборки (1%)
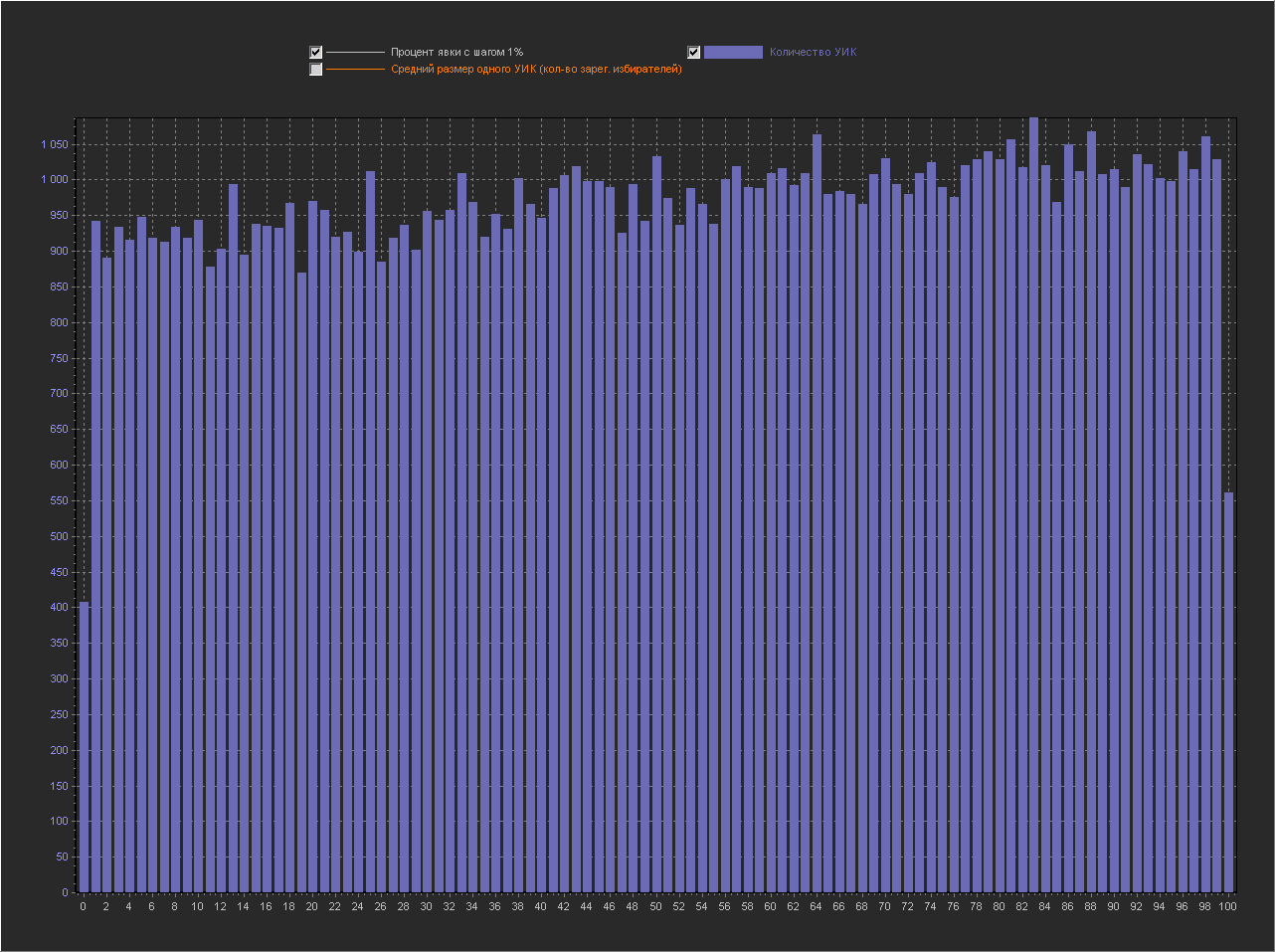
Шаг выборки (0.1%)
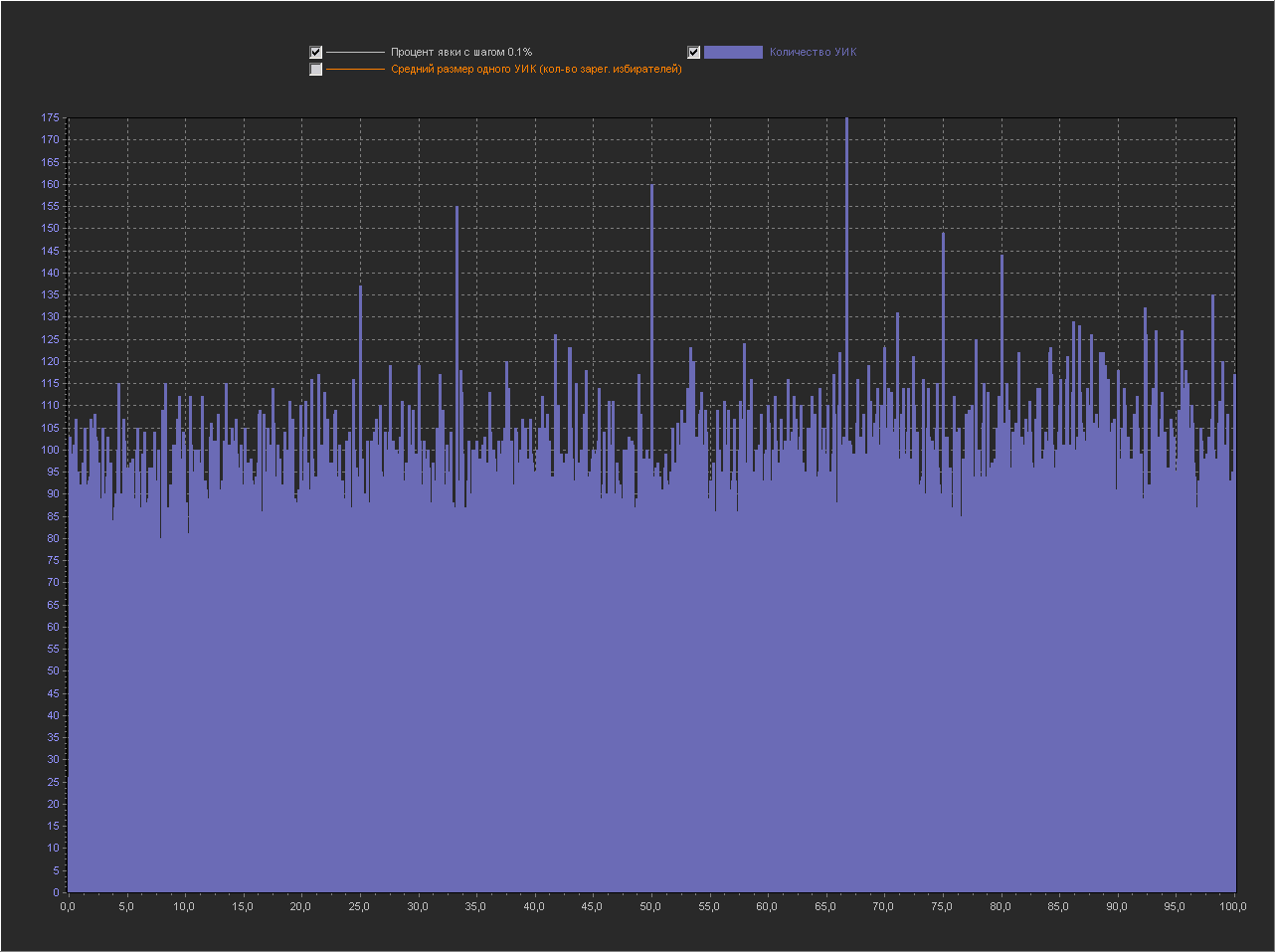
Шаг выборки (0.01%)
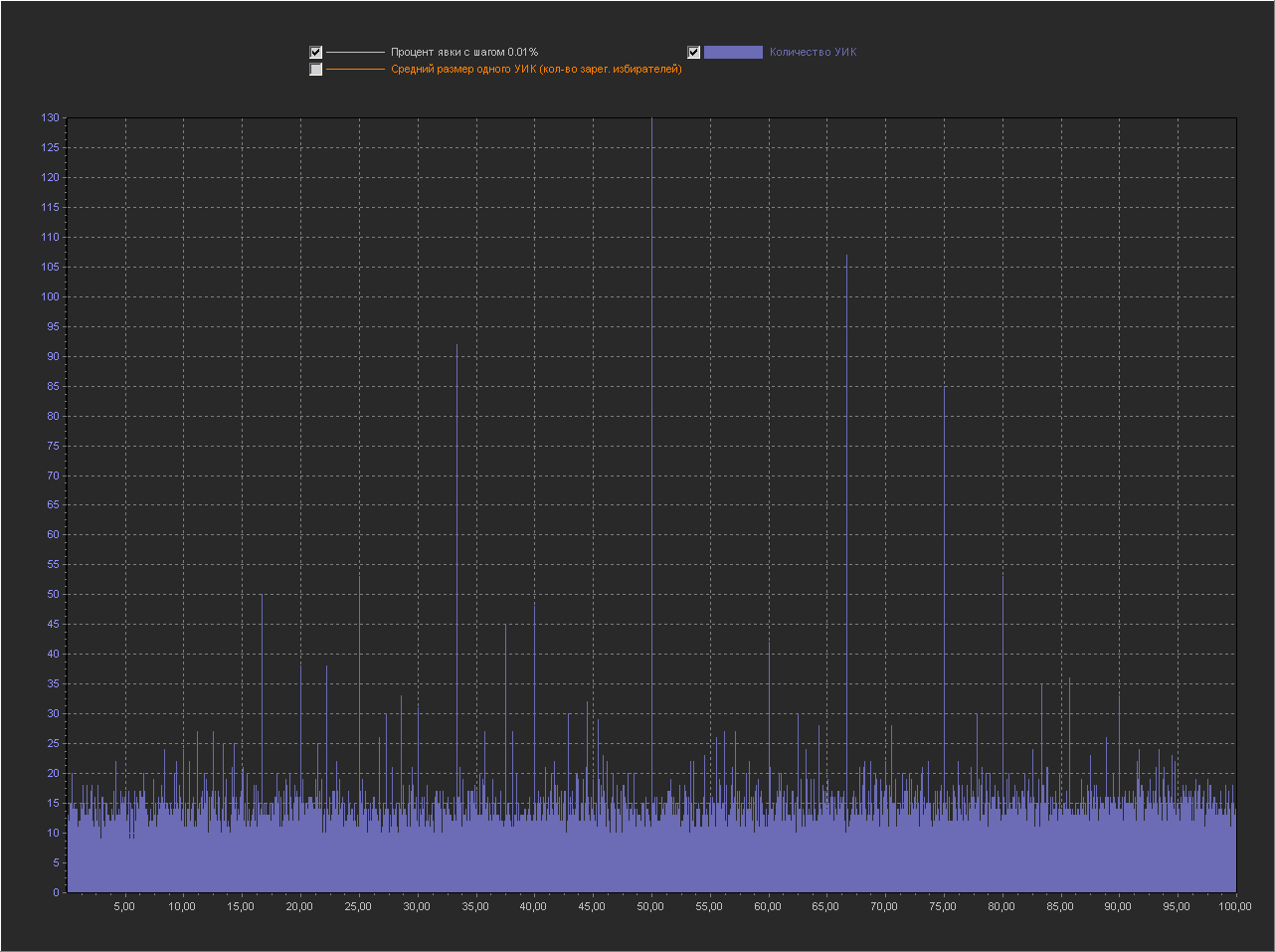
Шаг выборки (0.001%)
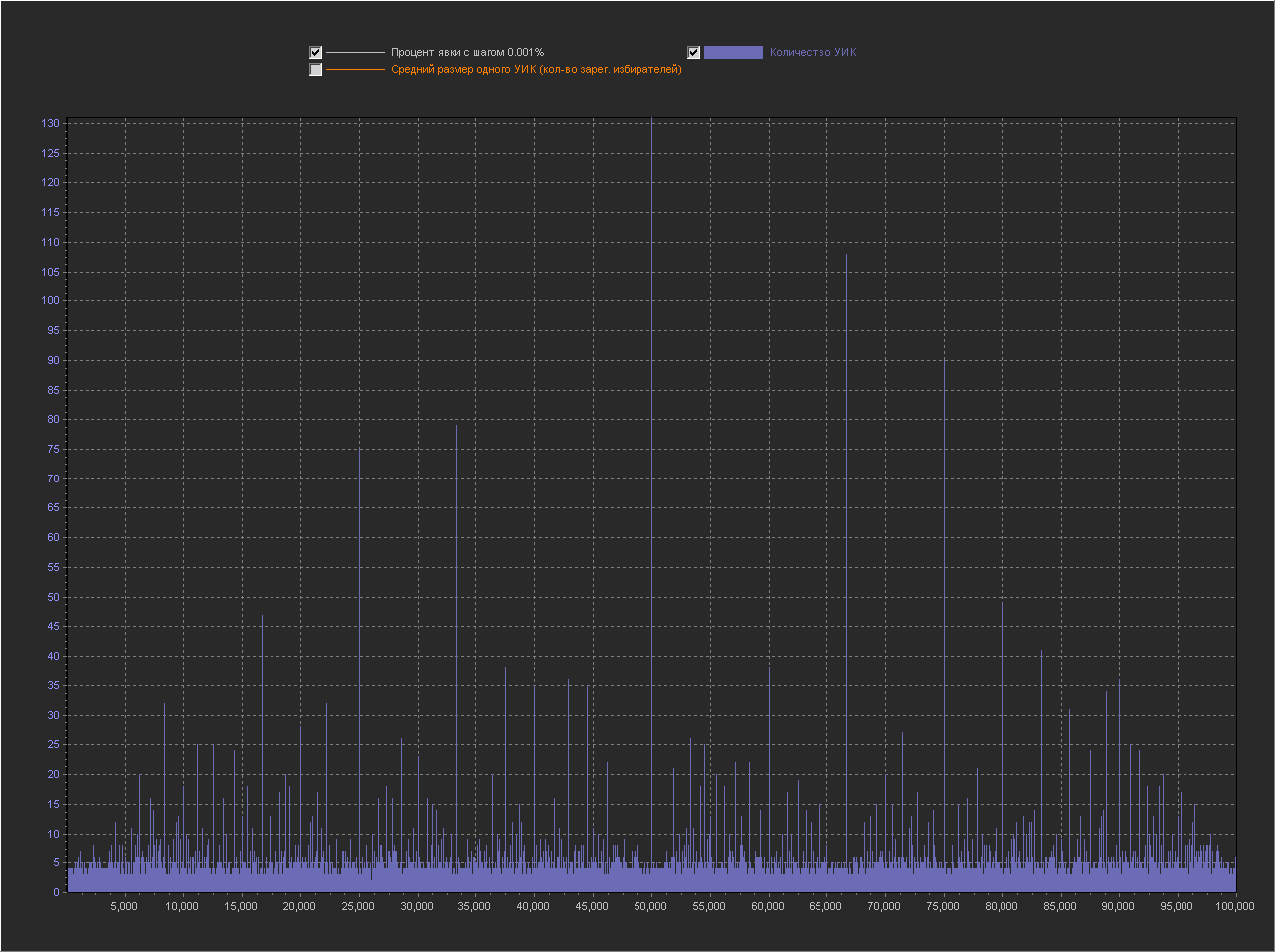
Таблицы из раздела «ключ»:
Общее разбиение по кратности количества зарегистрированных избирателей x2-10 для всех УИК:
KOLVO X2 X3 X4 X5 X6 X7 X8 X9 X10
97699 49413 32753 24724 20283 16649 13923 12464 10917 10411
KOLVO – общее кол-во УИК в которых проводились выборы
X2-10 – количество УИК в которых кол-во зарег. избирателей кратно 2-10
И общее разбиение по кратности пришедших на выборы избирателей x2-10 для всех УИК:
KOLVO X2 X3 X4 X5 X6 X7 X8 X9 X10
97699 49268 32712 24634 20608 16492 14085 12192 10938 10752
KOLVO – общее кол-во УИК в которых проводились выборы
X2-10 – количество УИК в которых кол-во пришедших избирателей кратно 2-10
Как работает модель:
0. По таблице рассчитывается вероятность появления числа кратного X2-X10
VerX2 = X2 / KOLVO
VerX3 = X3 / KOLVO
…
1. Запускается цикл по кол-ву УИКов = 97699
2. Для каждого УИКа случайно генерируется его размер из реального диапазона 3 — 7746 чел
3. В соответствии с вероятностью выбирается кратность УИКа, и от случайного размера УИКа — вычитается остаток от деления на кратное число. Если ни одна из вероятностей не сработала, то размер УИКа остается без изменения (случайным).
4. Случайно выбирается кол-во человек пришедших на выборы в УИК из диапазона 0… размер УИКа.
5. В соответствии с вероятностью выбирается кратность человек пришедших в УИК и от этого числа — вычитается остаток от деления на кратное число. Если ни одна из вероятностей не сработала, то кол-во человек остается без изменения (случайным).
6. Считается явка и в массиве результата соответствующему явке увеличивается кол-во УИК на +1.
7. По массиву результата строится график
Как видно из графиков на шаге 1%, пиков нет. На шаге 0.1% — есть, в том числе и на круглых значениях (90,85,80,75,70,65,60,50...). Сгенерировав график десяток раз можно подобрать конфигурацию пиков на свой вкус :) Такая длинная последовательность «круглых» чисел появляется не всегда, обычно есть пропуски или склеивания, но за примерно 10 генераций ее можно увидеть если искать по всему графику и учитывать все пики, а не только 5 самых высоких.
Замечания:
Естественно — это очень упрощенная модель выборов. Я бы сказал это модель выборов где в реальных УИКах все люди выбирают между пойти/не пойти на выборы подбрасывая монетку (поэтому пика 50% обычно выше других, хотя это не обязательно (например на графике с 0.1% я выбрал вариант где самая высокая пика не 50%)). Но как мы видим, само физическое распределение размера УИКов по кратности и кол-ва пришедших избирателей — уже является причиной появления пиков на «случайном выборе», а когда добавляется «разумный выбор» эти пики уже могут усиливаться или ослабляться в зависимости от распределения «разумного выбора».
Заключение:
Считаю, что показанная выше модель пиков вполне объясняет их возможность «естественного» происхождения и на реальном графике выборов (в силу того, что использует вероятности взятые из реальных данных). Пики — это не «аномалия», это скажем так, базовые классы, которые отображают некую обобщенную тенденцию выбора.
Но, я могу построить модель, которая будет использовать реальные данные по голосованию и мы посмотрим, что получится. В разделе «ключ» изначально были представлены таблицы с данными по кратности, я их выложил с самого начала, так как по моим прикидкам вероятности, которые они описывают, как раз и являются «ключом» к решению проблемы. Но формулы и расчеты это одно, а практика это другое… давайте проверим.
Вот визуализация, основанная на таблице кратности размеров УИК:
Шаг выборки (1%)

Шаг выборки (0.1%)

Шаг выборки (0.01%)

Шаг выборки (0.001%)

Таблицы из раздела «ключ»:
Общее разбиение по кратности количества зарегистрированных избирателей x2-10 для всех УИК:
KOLVO X2 X3 X4 X5 X6 X7 X8 X9 X10
97699 49413 32753 24724 20283 16649 13923 12464 10917 10411
KOLVO – общее кол-во УИК в которых проводились выборы
X2-10 – количество УИК в которых кол-во зарег. избирателей кратно 2-10
И общее разбиение по кратности пришедших на выборы избирателей x2-10 для всех УИК:
KOLVO X2 X3 X4 X5 X6 X7 X8 X9 X10
97699 49268 32712 24634 20608 16492 14085 12192 10938 10752
KOLVO – общее кол-во УИК в которых проводились выборы
X2-10 – количество УИК в которых кол-во пришедших избирателей кратно 2-10
Как работает модель:
0. По таблице рассчитывается вероятность появления числа кратного X2-X10
VerX2 = X2 / KOLVO
VerX3 = X3 / KOLVO
…
1. Запускается цикл по кол-ву УИКов = 97699
2. Для каждого УИКа случайно генерируется его размер из реального диапазона 3 — 7746 чел
3. В соответствии с вероятностью выбирается кратность УИКа, и от случайного размера УИКа — вычитается остаток от деления на кратное число. Если ни одна из вероятностей не сработала, то размер УИКа остается без изменения (случайным).
4. Случайно выбирается кол-во человек пришедших на выборы в УИК из диапазона 0… размер УИКа.
5. В соответствии с вероятностью выбирается кратность человек пришедших в УИК и от этого числа — вычитается остаток от деления на кратное число. Если ни одна из вероятностей не сработала, то кол-во человек остается без изменения (случайным).
6. Считается явка и в массиве результата соответствующему явке увеличивается кол-во УИК на +1.
7. По массиву результата строится график
Вот код на c++
int k_uchastok = 97699;
int arr[] = {49413 ,32753 ,24724 ,20283 ,16649 ,13923 ,12464 ,10917 ,10411};
std::vector<int> all_kratnost(arr, arr + sizeof(arr) / sizeof(int));
std::vector<double> ver_kratnost(all_kratnost.size());
for (int i = 0; i < all_kratnost.size(); i++)
{
ver_kratnost[i] = (double)all_kratnost[i] / (double)k_uchastok;
}
int arr2[] = {49268, 32712, 24634, 20608, 16492, 14085, 12192, 10938, 10752};
std::vector<int> all_kratnost2(arr2, arr2 + sizeof(arr2) / sizeof(int));
std::vector<double> ver_kratnost2(all_kratnost2.size());
for (int i = 0; i < all_kratnost2.size(); i++)
{
ver_kratnost2[i] = (double)all_kratnost2[i] / (double)k_uchastok;
}
for (int i = 0; i < k_uchastok; i++)
{
// Случайное значение от 0 до 1
double ver_value = (double)rand() / RAND_MAX ;
uik_size = 3 + rand()%7743;
int k;
for (k = 0; k < all_kratnost.size(); k++)
{
if (ver_value < ver_kratnost[k])
{
// кратно 2+k
int ostatok = uik_size % (k+2);
if (uik_size > (ostatok+3))
{
uik_size -= ostatok;
}
uik_yavka = uik_size - rand()%uik_size;
// Случайное значение от 0 до 1
double ver_value2 = (double)rand() / RAND_MAX ;
for (int k2 = 0; k2 < all_kratnost2.size(); k2++)
{
if (ver_value2 < ver_kratnost2[k2])
{
// кратно 2+k2
int ostatok = uik_yavka % (k2+2);
if (uik_yavka > ostatok)
{
uik_yavka -= ostatok;
}
break;
}
else
{
ver_value2 -= ver_kratnost2[k2];
}
}
procentx = (double)uik_yavka / uik_size;
procentx = RoundTo(procentx * 100.0, round_digits);
result_map[procentx] += 1;
break;
}
else
{
ver_value -= ver_kratnost[k];
}
}
// ни одна вероятность не сработала
if (k == all_kratnost.size())
{
uik_yavka = uik_size - rand()%uik_size;
procentx = (double)uik_yavka / uik_size;
procentx = RoundTo(procentx * 100.0, round_digits);
result_map[procentx] += 1;
}
}
std::map<double, int>::iterator it;
for (it = result_map.begin(); it != result_map.end(); ++it)
{
m_BarSeries_Bottom->AddXY(it->first, it->second);
}Как видно из графиков на шаге 1%, пиков нет. На шаге 0.1% — есть, в том числе и на круглых значениях (90,85,80,75,70,65,60,50...). Сгенерировав график десяток раз можно подобрать конфигурацию пиков на свой вкус :) Такая длинная последовательность «круглых» чисел появляется не всегда, обычно есть пропуски или склеивания, но за примерно 10 генераций ее можно увидеть если искать по всему графику и учитывать все пики, а не только 5 самых высоких.
Замечания:
Естественно — это очень упрощенная модель выборов. Я бы сказал это модель выборов где в реальных УИКах все люди выбирают между пойти/не пойти на выборы подбрасывая монетку (поэтому пика 50% обычно выше других, хотя это не обязательно (например на графике с 0.1% я выбрал вариант где самая высокая пика не 50%)). Но как мы видим, само физическое распределение размера УИКов по кратности и кол-ва пришедших избирателей — уже является причиной появления пиков на «случайном выборе», а когда добавляется «разумный выбор» эти пики уже могут усиливаться или ослабляться в зависимости от распределения «разумного выбора».
Заключение:
Считаю, что показанная выше модель пиков вполне объясняет их возможность «естественного» происхождения и на реальном графике выборов (в силу того, что использует вероятности взятые из реальных данных). Пики — это не «аномалия», это скажем так, базовые классы, которые отображают некую обобщенную тенденцию выбора.
Update3:
Еще более реальная модель по настоящим размерам УИКов из БД
Теперь мы не будем генерировать размеры УИКа случайно, а возьмем реально каждый УИК в БД с его реальным размером и сгенерируем для него абсолютно случайную явку от 0 до размера УИКа.
Т.е. в симуляции мы полностью воспроизводим выборы в РФ на всех реально существующих в ней УИКах, но «разумный выбор» заменяем монеткой «пойти/не пойти».
График для шага 1%
(Пики на ровно «круглых» значениях с кратностью 5 выделены желтой линией. Подсвечиваются все пики в которых ровно круглое значение выше чем ближайшие справа и слева.).

Графики для шага 0.1%
Привожу для примера 5 генераций.
1
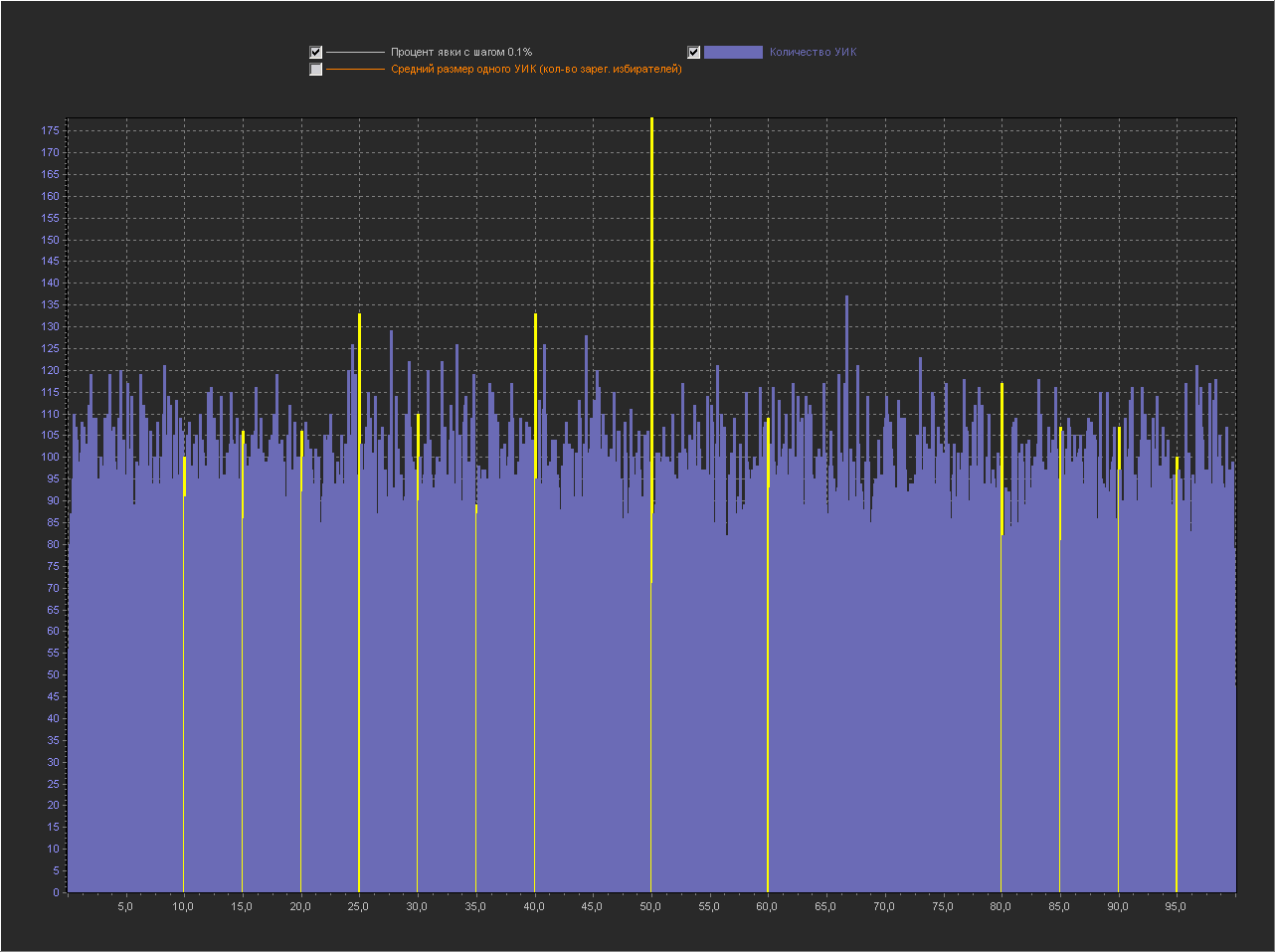
2

3
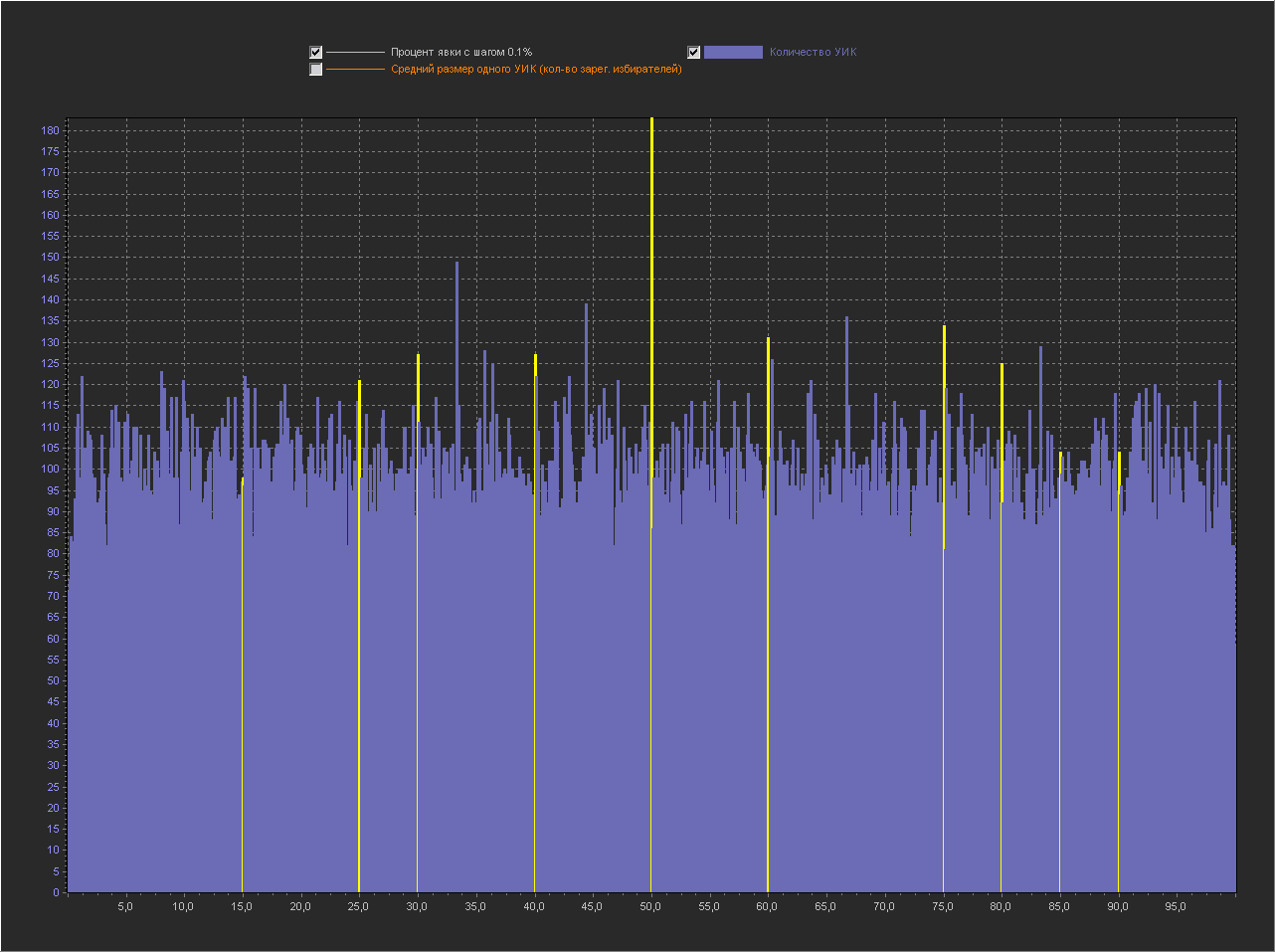
4
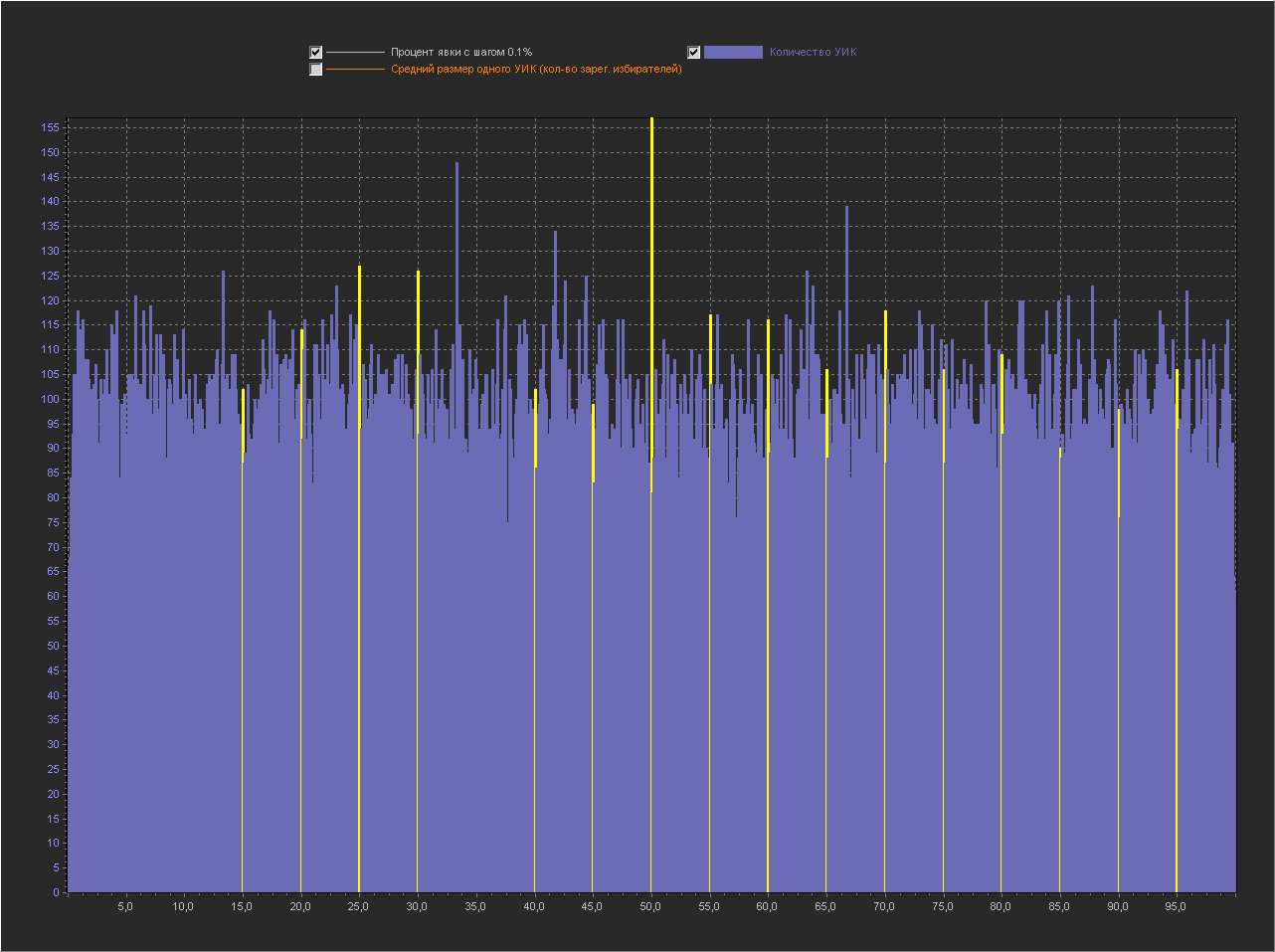
5
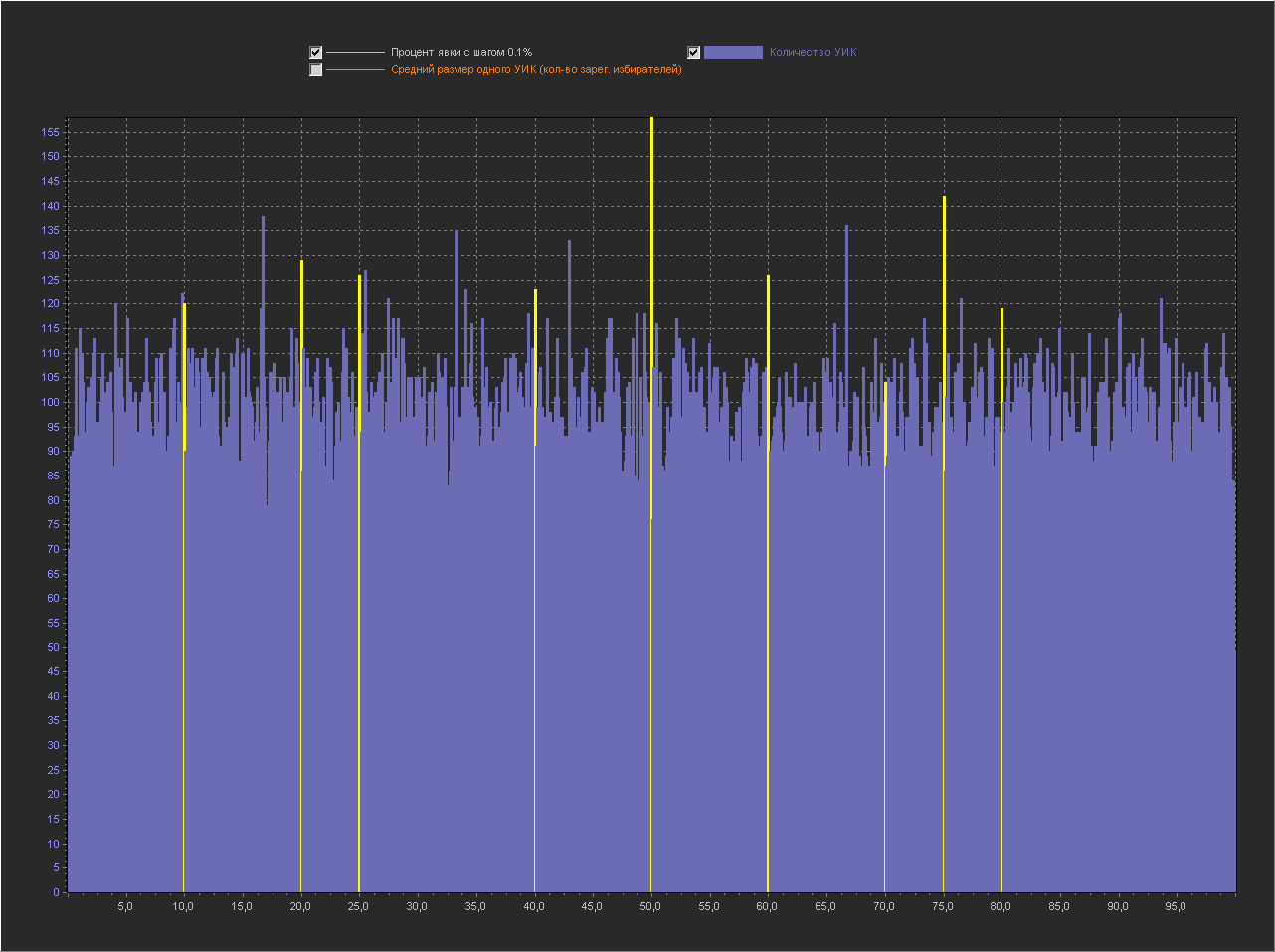
Графики для шага 0.01%

Графики для шага 0.001%

Выводы:
1. Мы видим — что пики это абсолютно нормальное явление на шаге 0.1% и тем более на 0.01% и 0.001%.
2. Мы видим, что пики на ровно «круглых» значениях с кратностью 5 — стабильно существуют на графике обычно в диапазоне (9 — 16 шт).
3. На шаге 0.001% — пики на «круглых» значениях включают в себя только ровно то количество УИКов, которое к ним относится. Далее при увеличении шага и округлении, к пикам добавляются значения из их ближайших окрестностей. При этом высота пик на «круглых» значениях перестает доминировать, на 0.01% это не очень заметно, а вот на графике 0.1% мы в зависимости от случайности в генерации уже можем увидеть наличие последовательности высоких пик на круглых значениях (сравнимых с самыми высокими пиками на графике) реже, но они стабильно появляются на графике.
Можно сказать, что существование высоких пик на круглых значениях с шагом 0.001% — связано с более высокой вероятностью появления целого значения в дроби при расчете явки. А вот дальнейшее распределение пик при более мелких шагах с округлением, уже больше зависит от «разумного выбора».
При симуляции выборов по реальному кол-ву и размерам УИКов мы использовали логику подбрасывания монетки, естественно результаты такой симуляции нельзя напрямую сравнивать с результатами реального голосования но, мы точно показали что:
Теперь мы не будем генерировать размеры УИКа случайно, а возьмем реально каждый УИК в БД с его реальным размером и сгенерируем для него абсолютно случайную явку от 0 до размера УИКа.
Т.е. в симуляции мы полностью воспроизводим выборы в РФ на всех реально существующих в ней УИКах, но «разумный выбор» заменяем монеткой «пойти/не пойти».
График для шага 1%
(Пики на ровно «круглых» значениях с кратностью 5 выделены желтой линией. Подсвечиваются все пики в которых ровно круглое значение выше чем ближайшие справа и слева.).

Графики для шага 0.1%
Привожу для примера 5 генераций.
1

2

3

4

5

Графики для шага 0.01%

Графики для шага 0.001%

Выводы:
1. Мы видим — что пики это абсолютно нормальное явление на шаге 0.1% и тем более на 0.01% и 0.001%.
2. Мы видим, что пики на ровно «круглых» значениях с кратностью 5 — стабильно существуют на графике обычно в диапазоне (9 — 16 шт).
3. На шаге 0.001% — пики на «круглых» значениях включают в себя только ровно то количество УИКов, которое к ним относится. Далее при увеличении шага и округлении, к пикам добавляются значения из их ближайших окрестностей. При этом высота пик на «круглых» значениях перестает доминировать, на 0.01% это не очень заметно, а вот на графике 0.1% мы в зависимости от случайности в генерации уже можем увидеть наличие последовательности высоких пик на круглых значениях (сравнимых с самыми высокими пиками на графике) реже, но они стабильно появляются на графике.
Можно сказать, что существование высоких пик на круглых значениях с шагом 0.001% — связано с более высокой вероятностью появления целого значения в дроби при расчете явки. А вот дальнейшее распределение пик при более мелких шагах с округлением, уже больше зависит от «разумного выбора».
При симуляции выборов по реальному кол-ву и размерам УИКов мы использовали логику подбрасывания монетки, естественно результаты такой симуляции нельзя напрямую сравнивать с результатами реального голосования но, мы точно показали что:
- Пики на круглых значениях стабильно существуют на нашем голосовании монеткой и это является подтверждением их «естественности».
- Размеры пик на «круглых» значениях сопоставимы по размерам с пиками на «не круглых» значениях, но редко могут на много превышать другие пики с не круглыми значениями. Поэтому появление высоких пик на круглых значениях в реальном голосовании, показанная нами «естественность» не объясняет. Но, то что они существуют и могут быть усилены «разумным выбором» вполне вероятно.
P.S.
Да и еще, в виду отрицательной кармической ситуации не могу отвечать сразу всем на комментарии в статье, поэтому кому пока не ответил извините :)