Предисловие
В этой статье речь пойдет о методах решения задач математической оптимизации, основанных на использовании градиента функции. Основная цель — собрать в статье все наиболее важные идеи, которые так или иначе связаны с этим методом и его всевозможными модификациями.
UPD. В комментариях пишут, что на некоторых браузерах и в мобильном приложении формулы не отображаются. К сожалению, не знаю, как с этим бороться. Могу лишь сказать, что использовал макросы «inline» и «display» хабравского редактора. Если вдруг знаете, как это исправить — напишите в комментариях, пожалуйста.
Примечание от автора
На момент написания я защитил диссертацию, задача которой требовала от меня глубокое понимание теоретических основно методов математической оптимизации. Тем не менее, у меня до сих пор (как и у всех) расплываются глаза от страшных длинных формул, поэтому я потратил немалое время, чтобы вычленить ключевые идеи, которые бы характеризовали разные вариации градиентных методов. Моя личная цель — написать статью, содержащую минимальное количество информации, необходимое для более менее подробного понимания тематики. Но будьте готовы, без формул так или иначе не обойтись.
Постановка задачи
Прежде чем описывать метод, следует сначала описать задачу, а именно: «Даны множество
В теории обычно предполагается, что
Немного математики
Допустим пока что нам нужно просто найти минимум одномерной функции
Еще в 17 веке Пьером Ферма был придуман критерий, который позволял решать простые задачи оптимизации, а именно, еcли
где
Чем ближе
Величина
Стоит отметить, что указанные условия являются необходимыми, но не достаточными, самый простой пример — 0 для
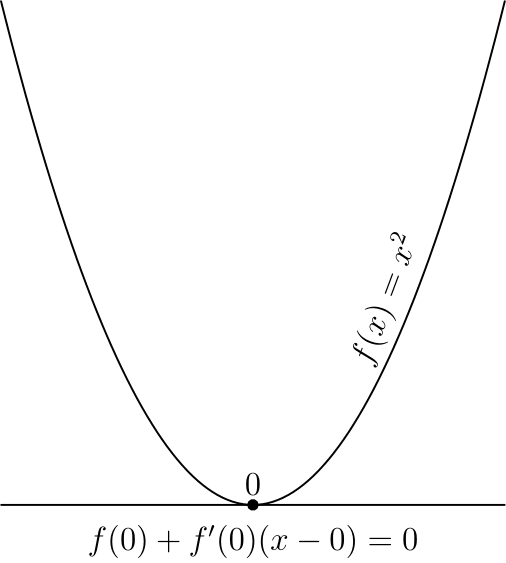
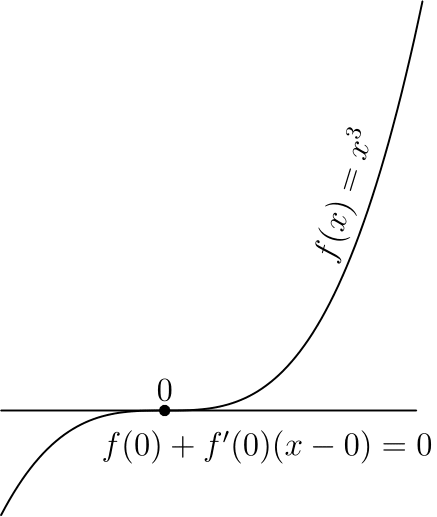
Этот критерий является достаточным в случае выпуклой функции, во многом из-за этого для выпуклых функций удалось получить так много результатов.
Квадратичные функции
Квадратичные функции в
Для экономии места (да и чтобы меньше возиться с индексами) такую функцию обычно записывают в матричной форме:
где
Зачем я об этом рассказываю? Дело в том, что квадратичные функции важны в оптимизации по двум причинам:
- Они тоже встречаются на практике, например при построении линейной регрессии методом наименьших квадратов
- Градиент квадратичной функции — линейная функция, в частности для функции выше
Или в матричной форме
Таким образом система— линейная система. Системы, проще чем линейная, просто не существует. Мысль, к которой я старался подобраться — оптимизация квадратичной функции — самый простой класс задач оптимизации. С другой стороны, тот факт, что
— необходимые условия минимума дает возможность решать линейные системы через задачи оптимизации. Чуть позже я постараюсь вас убедить в том, что это имеет смысл.
Полезные свойства градиента
Хорошо, мы вроде бы выяснили, что если функция дифференцируема (у нее существуют производные по всем переменным), то в точке минимума градиент должен быть равен нулю. А вот несет ли градиент какую-нибудь полезную информацию в случае, когда он отличен от нуля?
Попробуем пока решить более простую задачу: дана точка
Аналогично, если
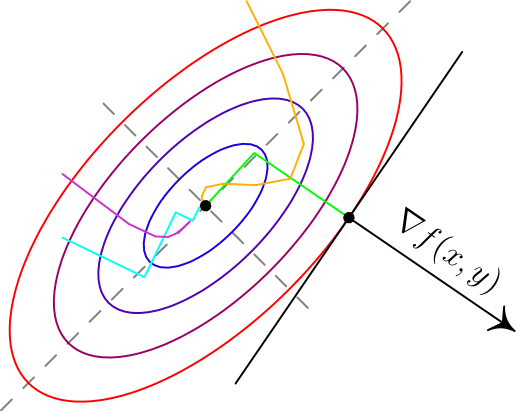
Вот два примера для двумерных функций. Такого рода картинки можно часто увидеть в демонстрациях градиентного спуска. Цветные линии — так называемые линии уровня, это множество точек, для которых функция принимает фиксированное значений, в моем случае это круги и эллипсы. Я обозначил синими линии уровня с более низким значением, красными — с более высоким.
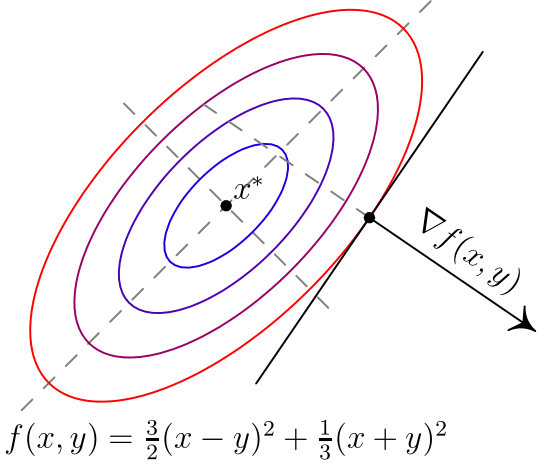
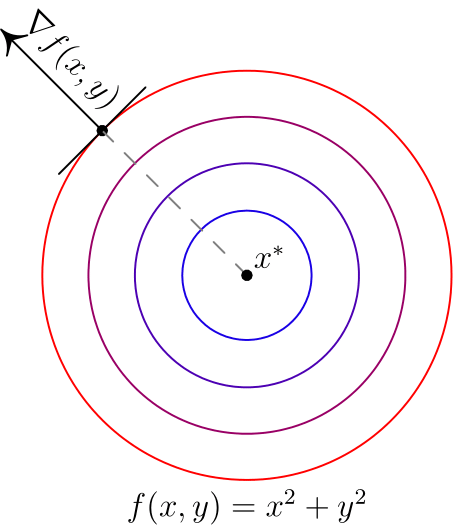
Обратите внимание, что для поверхности, заданной уравнением вида
Градиентный спуск
До базового метода градиентного спуска остался лишь малый шажок: мы научились по точке
Величина
для всех
Анализ для квадратичных функций
Если
где
Выражение слева — расстояние от приближения, полученного на шаге
Модификации градиентного спуска
Теперь хотелось бы рассказать немного про часто используемые модификации градиентного спуска, в первую очередь так называемые
Инерционные или ускоренные градиентные методы
Все методы такого класса выражаются в следующем виде
Последнее слагаемое характеризует эту самую «инерционность», алгоритм на каждом шаге старается двигаться против градиента, но при этом по инерции частично двигается в том же направлении, что и на предыдущей итерации. Такие методы обладают двумя важными свойствами:
- Они практически не усложняют обычный градиентный спуск в вычислительном плане.
- При аккуратном подборе
такие методы на порядок быстрее, чем обычный градиентный спуск даже с оптимально подобранным шагом.
Один из первых таких методов появился в середине 20 века и назывался метод тяжелого шарика, что передавало природу инерционности метода: в этом методе
Метод тяжелого шарика — самый простой инерционный метод, но не самый первый. При этом, на мой взгляд, самый первый метод довольно важен для понимания сути этих методов.
Метод Чебышева
Да да, первый метод такого типа был придуман еще Чебышевым для решения систем линейных уравнений. В какой-то момент при анализе градиентного спуска было получено следующее равенство
где
поэтому их невозможно построить для градиентного спуска, который вычисляет новое значение лишь по одному предыдущему, а для инерционных становится возможным за счет того, что используется два предыдущих значения. При этом оказывается, что сложность вычисления
Метод сопряженных градиентов
Еще один очень интересный и важный факт (следствие теоремы Гамильтона-Кэли): для любой квадратной матрицы
Если бы мы могли подбирать размер шага в градиентном спуске так, чтобы получать именно этот обнуляющий многочлен, то градиентный спуск сходился бы за фиксированное число итерации не большее размерности
- Одна итерация градиентного спуска (без учета вычислений параметров) содежит одно умножение матрицы на вектор и 2-3 сложения векторов
- Вычисление параметров также требует 1-2 умножение матрицы на вектор, 2-3 скалярных умножения вектор на вектор и несколько сложений векторов.
Самое сложное в вычислительном плане — умножение Матрицы на вектор, обычно это делается за время
Метод сопряженных градиентов хорошо работает и в случае, если
Метод Нестерова
Для сообществ математической оптимизации и машинного обучения фамилия «Нестеров» уже давно стало нарицательной. В 80х годах прошлого века Ю.Е. Нестеров придумал интересный вариант инерционного метода, который имеет вид
при этом не предполагается какого-то сложного подсчета
Стохастический градиентный спуск
Единственное формальное отличие от обычного градиентного спуска — использование вместо градиента функции
и
Если
Стоит отметить, что идеи иннерционных методов применяются для стохастического градиентного спуска и на практике часто дают прирост, в теории же обычно считается, что асимптотическая скорость сходимости не меняется из-за того, что основная погрешность в стохастическом градиентном спуске обусловлена дисперсией
Субградиентный спуск
Эта вариация позволяет работать с недифференцируемыми функциями, её я опишу более подробно. Придется опять вспомнить линейное приближение — дело в том, что есть простая характеристика выпуклости через градиент, дифференцируемая функция
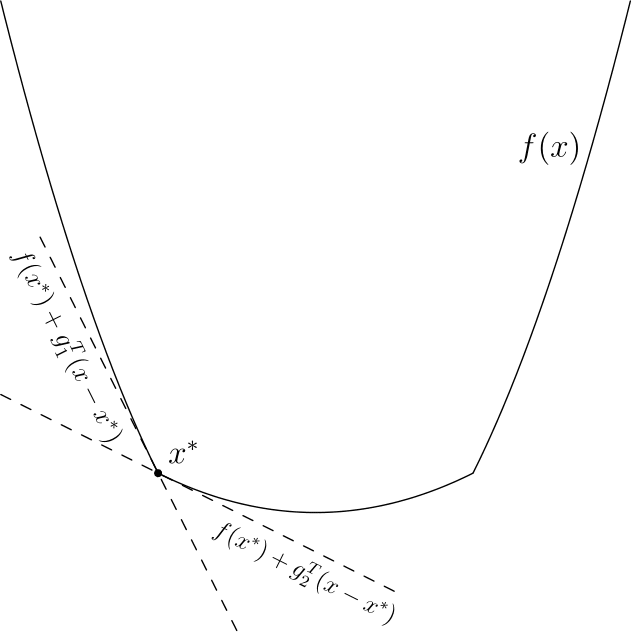
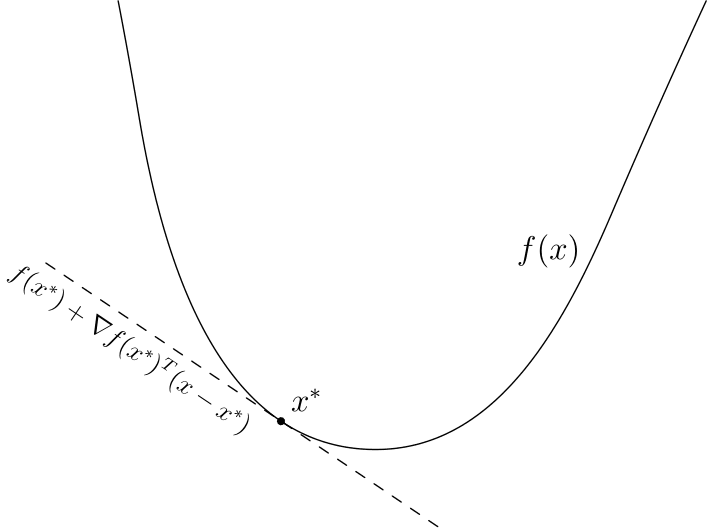
Вычислить хотя бы один субградиент для точки обычно не очень сложно, субградиентный спуск по сути использует субградиент вместо градиента. Оказывается — этого достаточно, в теории скорость сходимости при этом падает, однако например в нейронных сетях недифференцируемую функцию
Пожалуй, последняя важная вещь, которую стоит знать, — это то, что субградиентный спуск не сходится при постоянном размере шага. Это проще всего увидеть для указанной выше функции
- Допустим мы начали из точки
.
- Шаг субградиентного спуска:
- Если
, то первые несколько шагов мы будет вычитать единицу, если
, то прибавлять. Так или иначе мы в какой-то момент окажемся на интервале
, из которого попадем в
, а дальше будем прыгать между двумя точками этих интервалов.
В теории для субградиентного спуска рекомендуется брать последовательность шагов
Где
Proximal методы
К сожалению я не знаю хорошего перевода для «proximal» в контексте оптимизации, поэтому просто так и буду называть этот метод. Proximal-методы появились как обобщение проективных градиентных методов. Идея очень простая: если есть функция
Думаю, пока что совершенно непонятно, зачем это может понадобиться, особенно учитывая то, что я не объяснил, что такое proximal-оператор. Вот два примера:
— индикатор-функция выпуклого множества
, то есть
В этом случае— это проекция на множество
, то есть «ближайшая к
точка множества
». Таким образом, мы ограничиваем градиентный спуск только на множество
, что позволяет решать задачи с ограничениями. К сожалению, вычисление проекции в общем случае может быть еще более сложной задачей, поэтому обычно такой метод применяется, если ограничения имеют простой вид, например так называемые box-ограничения: по каждой координате
—
-регуляризация. Такое слагаемое любят добавлять в задачи оптимизации в машинном обучении, чтобы избежать переобучения. Регуляризация такого вида еще и имеет тенденцию обнулять наименее значимые компоненты. Для такой функции proximal-оператор имеет вид (ниже описано выражение для одной координаты):
что довольно просто вычислить.
Заключение
На этом заканчиваются основные известные мне вариации градиентного метода. Пожалуй под конец я бы отметил, что все указанные модификации (кроме разве что метода сопряженных градиентов) могут легко взаимодействовать друг с другом. Я специально не стал включать в эту перечень метод Ньютона и квазиньютоновские методы (BFGS и прочие): они хоть и используют градиент, но при этом являются более сложными методами, требуют специфических дополнительных вычислений, которые обычно более вычислительно затратны, нежели вычисление градиента. Тем не менее, если этот текст будет востребован, я с удовольствием сделаю подобный обзор и по ним.
Использованная / рекомендованная литература
Boyd. S, Vandenberghe L. Convex Optimization
Shewchuk J. R. An Introduction to the Conjugate Gradient Method Without the Agonizing Pain
Bertsekas D. P. Convex Optimization Theory
Нестеров Ю. Е. Методы выпуклой оптимизации
Гасников А. В. Универсальный градиентный спуск