На самом деле, он самый. Но обо всём по порядку.
Осваиваю питон, решаю всякое на Codewars. Сталкиваюсь с известной задачей про небоскрёб и яйца. Разница лишь в том, что исходные данные — не 100 этажей и 2 яйца, а чуть побольше.
Дано: N яиц, M попыток их бросить, бесконечный небоскрёб.
Определить: максимальный этаж, с которого можно бросить яйцо, не разбив. Яйца сферические в вакууме и, если одно из них не разбилось, упав, например, с 99-го этажа, то остальные тоже выдержат падение со всех этажей меньше сотого.
0 <= N, M <= 20000.
Время прогона двух десятков тестов — 12 секунд.
Нужно написать функцию height(n, m), которая будет возвращать номер этажа для заданных n,m. Так как упоминаться она будет очень часто, а писать каждый раз «height» лень, то везде, кроме кода обозначу её, как f(n, m).
Начнём с нулей. Очевидно, что если нет яиц или попыток их бросить, то определить ничего нельзя и ответом будет ноль. f(0, m) = 0, f(n, 0) = 0.
Допустим, яйцо одно, а попыток 10. Можно рискнуть всем и бросить его сразу с сотого этажа, но в случае неудачи, определить больше ничего не удастся, так что логичнее всё же начинать с первого этажа и подниматься вверх на один этаж после каждого броска, пока не кончатся либо попытки, либо яйцо. Максимум, куда получится добраться, если яйцо не подведёт — этаж номер 10. f(1, m) = m
Возьмём второе яйцо, попыток опять 10. Теперь-то можно рискнуть с сотого? Разобьётся — останется ещё одно и 9 попыток, хотя бы 9 этажей получится пройти. Так может и рисковать нужно не с сотого, а с десятого? Логично. Тогда, в случае успеха, останется 2 яйца и 9 попыток. По аналогии, теперь нужно подняться ещё на 9 этажей. При серии успехов — ещё на 8, 7, 6, 5, 4, 3, 2 и 1. Итого, мы на 55-ом этаже с двумя целыми яйцами и без попыток. Ответом видится сумма первых M членов арифметической прогрессии с первым членом 1 и шагом 1. f(2, m) = (m*m + m) / 2. А ещё видно, что на каждом шаге как бы происходил вызов функции f(1, m), но это пока не точно.
Продолжим с тремя яйцами и десятью попытками. В случае неудачного первого броска, прикрыты снизу будут этажи, определяемые 2 яйцами и 9 попытками, а это значит, что первый бросок надо совершать с этажа f(2, 9) + 1. Тогда, в случае успеха, имеем 3 яйца и 9 попыток. И для второй попытки нужно подняться ещё на f(2,8) + 1 этажей. И так далее, пока на руках не останется 3 яйца и 3 попытки. И тут самое время отвлечься на рассмотрение случаев с N=M, когда яиц столько же, сколько и попыток.
Вернёмся к f(3, 10). По сути, на каждом шаге всё сводится к сумме f(2, m-1) — количеству этажей, которые можно определить в случае неудачи, единицы и f(3, m-1) — количеству этажей, которые можно определить в случае успеха. И становится понятно, что от увеличения количества яиц и попыток вряд ли что-то изменится. f(n, m) = f(n — 1, m — 1) + 1 + f(n, m — 1). И это универсальная формула, можно воплощать в коде.
Разумеется, предварительно я наступил на грабли немемоизирования рекурсивных функций и узнал, что f(10, 40) выполняется почти 40 секунд с количеством вызов самой себя — 97806983. Но и мемоизация спасает только на начальных интервалах. Если f(200,400) выполняется за 0.8 секунды, то f(200, 500) уже за 31 секунду. Забавно, что при замере времени выполнения с помощью %timeit, то результат получается куда меньше реального. Очевидно, что первый прогон функции занимает большую часть времени, а остальные просто пользуются результатами его мемоизации. Ложь, наглая ложь и статистика.
Итак, в тестах фигурирует, например, f(9477, 10000), а у меня жалкая f(200, 500) уже не укладывается в нужное время. Значит есть другое решение, без рекурсии, продолжим его поиски. Дополнил код подсчетом вызовов функции с определёнными параметрами, чтобы посмотреть на что она в итоге раскладывается. Для 10 попыток получились такие результаты:
f(3,10) = 7+ 1*f(2,9)+ 1*f(2,8)+ 1*f(2,7)+ 1*f(2,6)+ 1*f(2,5)+ 1*f(2,4)+ 1*f(2,3)+ 1*f(3,3)
f(4,10) = 27+ 1*f(2,8)+ 2*f(2,7)+ 3*f(2,6)+ 4*f(2,5)+ 5*f(2,4)+ 6*f(2,3)+ 6*f(3,3)+ 1*f(4,4)
f(5,10) = 55+ 1*f(2,7)+ 3*f(2,6)+ 6*f(2,5)+ 10*f(2,4)+ 15*f(2,3)+ 15*f(3,3)+ 5*f(4,4)+ 1*f(5,5)
f(6,10) = 69+ 1*f(2,6)+ 4*f(2,5)+ 10*f(2,4)+ 20*f(2,3)+ 20*f(3,3)+ 10*f(4,4)+ 4*f(5,5)+ 1*f(6,6)
f(7,10) = 55+ 1*f(2,5)+ 5*f(2,4)+ 15*f(2,3)+ 15*f(3,3)+ 10*f(4,4)+ 6*f(5,5)+ 3*f(6,6)+ 1*f(7,7)
f(8,10) = 27+ 1*f(2,4)+ 6*f(2,3)+ 6*f(3,3)+ 5*f(4,4)+ 4*f(5,5)+ 3*f(6,6)+ 2*f(7,7)+ 1*f(8,8)
f(9,10) = 7+ 1*f(2,3)+ 1*f(3,3)+ 1*f(4,4)+ 1*f(5,5)+ 1*f(6,6)+ 1*f(7,7)+ 1*f(8,8)+ 1*f(9,9)
Какая-то закономерность просматривается:

Коэффициенты эти теоретически рассчитываются. Каждый голубой — сумма верхнего и левого. А фиолетовые — те же самые голубые, только в обратном порядке. Рассчитать можно, но это же опять рекурсия, а в ней я разочаровался. Скорее всего, многие (жаль, что не я) уже узнали эти числа, но я пока сохраню интригу, следуя своему пути решения. Решил на них плюнуть и зайти с другой стороны.
Открыл эксель, соорудил табличку с результатами работы функции и стал высматривать закономерности. С3=ЕСЛИ(C$2>$B3;2^$B3-1;C2+B2+1), где $2 — строка с количеством яиц (1-13), $B — столбец с количеством попыток (1-20), C3 — ячейка на пересечении двух яиц и одной попытки.

Серая диагональ это N=M и тут наглядно видно, что справа от неё (при N > M) ничего не меняется. Видно — да иначе и быть не может, ведь это все результаты работы формулы, в которой так и задано- что каждая ячейка равна сумме верхней, верхней слева и единицы. Но какой-то универсальной формулы, куда можно подставить N и M и получить номер этажа, найти не удалось. Спойлер: её и не существует. Но зато так просто создание этой таблицы в экселе выглядит, может быть можно сгенерировать такую же питоном и таскать из неё ответы?
Вспоминаю, что существует NumPy, который как раз предназначен для работы с многомерными массивами, почему бы не попробовать его? Для начала нам понадобится одномерный массив из нулей размером в N+1 И одномерный массив из единиц размером в N. Берём первый массив от нулевого до предпоследнего элемента, складываем поэлементно с первым же массивом от первого элемента до последнего и с массивом единиц. К получившемуся массиву в начало добавляем ноль. Повторять M раз. Элемент номер N получившегося массива и будет ответом. Первые 3 шага выглядят так:

NumPy работает так быстро, что сохранять всю таблицу я не стал — каждый раз считал нужную строку заново. Одно но — результат работы на больших числах был неправильный. Старшие разряды вроде те, а младшие — нет. Так выглядят накопившиеся от многократного сложения погрешности арифметики чисел с плавающей точкой. Не беда — можно же изменить тип массива на int. Нет, беда — оказалось, что NumPy ради быстродействия работает только со своими типами данных, а его int, в отличие от питоновского int, может быть не больше 2^64-1, после чего молча переполняется и продолжается с -2^64. А у меня вообще-то ожидаются числа под три тысячи знаков. Зато работает очень быстро, f(9477, 10000) выполняется 233 мс, просто на выходе ерунда какая-то получается. Код даже приводить не буду, раз такое дело. Попробую сделать то же самое чистым питоном.
44 секунды на расчет f(9477, 10000), многовато. Но зато абсолютно точно. Что можно оптимизировать? Первое — нет нужды считать всё, что правее диагонали M,M. Второе — ни к чему считать последний массив целиком, ради одной-то ячейки. Для этого сгодятся две последние две ячейки предыдущего. Для вычисления f(10, 20) будет достаточно только вот этих серых ячеек:

И так это выглядит в коде:
И что вы думаете? f(9477, 10000) за 2 секунды! Но эти входные данные слишком хороши, длина массива на любом этапе будет не больше 533 элементов (10000-9477). Проверим на f(5477, 10000) — 11 секунд. Тоже хорошо, но только по сравнению с 44 секундами — двадцать тестов с таким временем не пройдёшь.
Всё не то. Но раз есть задача, значит есть и решение, поиски продолжаются. Я снова стал смотреть в экселевскую таблицу. Ячейка слева от (m, m) всегда на единицу меньше. А ячейка слева от неё уже нет, в каждой строке разность становится больше. Ячейка снизу от (m, m) всегда вдвое больше. А ячейка снизу от неё — уже не вдвое, а чуть меньше, но для каждого столбца по разному, чем дальше, тем больше. А ещё числа в одной строке сначала растут быстро, а после середины медленно. Дай-ка я построю таблицу разностей между соседними ячейками, может там какая закономерность появится?
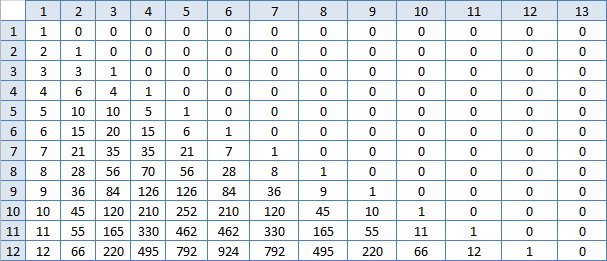
Ба, знакомые числа! То есть сумма N этих числе в строке номер M это и есть ответ? Правда, считать их — примерно то же самое, что я уже делал, вряд ли это сильно ускорит работу. Но надо попробовать:
Не сказать, что более оптимальное решение. На каких-то данных работает быстрее, на каких-то медленнее. Надо отправляться глубже. Что это за треугольник с числами, что появился в решении дважды? Стыдно признаться, но высшую математику, где треугольник наверняка фигурировал, я благополучно позабыл, так что пришлось гуглить.
Треугольник Паскаля, так он официально называется. Бесконечная таблица биномиальных коэффициентов. Так что ответом на задачу с N яйцами и M бросками является сумма первых N коэффициентов в разложении бинома Ньютона M-ой степени, кроме нулевого.
Произвольный биномиальный коэффициент может быть вычислен через факториалы номера строки и номера коэффициента в строке: bk = m!/(n!*(m-n!)). Но самое приятное — можно последовательно рассчитать числа в строке, зная её номер и нулевой коэффициент (всегда единица): bk[n] = bk[n-1] * (m — n + 1) / n. На каждом шаге числитель уменьшается на единицу, а знаменатель увеличивается. И лаконичное финальное решение выглядит так:
33 мс. на расчёт f(9477, 10000)! Это решение тоже можно оптимизировать, хотя в заданных диапазонах и оно отлично работает. Если n лежит во второй половине треугольника, то можно инвертировать его в m-n, посчитать сумму первых n коэффициентов и отнять её от 2^m-2. Если n близко к середине и m нечётное, то расчеты тоже можно сократить: сумма первой половины строки будет равна 2^(m-1)-1, последний коэффициент в первой половине можно рассчитать через факториалы, его номер это (m-1)/2, а дальше либо продолжаем прибавлять коэффициенты, если n в правой половине треугольника, либо отнимать, если в левой. Если m чётное, то половину строки уже не посчитаешь, но можно найти сумму первых m/2+1 коэффициентов, посчитав через факториалы средний и прибавив половину его к 2^(m-1)-1. На входных данных в районе 10^6 это очень заметно уменьшает время выполнения.
Уже после успешного решения, стал искать чьи-нибудь ещё изыскания по этому вопросу, но нашёл только то самое, с собеседований, с всего лишь двумя яйцами, а это не спортивно. Интернет будет неполон без моего решения, решил я, и вот оно.
Постановка задачи
Осваиваю питон, решаю всякое на Codewars. Сталкиваюсь с известной задачей про небоскрёб и яйца. Разница лишь в том, что исходные данные — не 100 этажей и 2 яйца, а чуть побольше.
Дано: N яиц, M попыток их бросить, бесконечный небоскрёб.
Определить: максимальный этаж, с которого можно бросить яйцо, не разбив. Яйца сферические в вакууме и, если одно из них не разбилось, упав, например, с 99-го этажа, то остальные тоже выдержат падение со всех этажей меньше сотого.
0 <= N, M <= 20000.
Время прогона двух десятков тестов — 12 секунд.
Поиск решения
Нужно написать функцию height(n, m), которая будет возвращать номер этажа для заданных n,m. Так как упоминаться она будет очень часто, а писать каждый раз «height» лень, то везде, кроме кода обозначу её, как f(n, m).
Начнём с нулей. Очевидно, что если нет яиц или попыток их бросить, то определить ничего нельзя и ответом будет ноль. f(0, m) = 0, f(n, 0) = 0.
Допустим, яйцо одно, а попыток 10. Можно рискнуть всем и бросить его сразу с сотого этажа, но в случае неудачи, определить больше ничего не удастся, так что логичнее всё же начинать с первого этажа и подниматься вверх на один этаж после каждого броска, пока не кончатся либо попытки, либо яйцо. Максимум, куда получится добраться, если яйцо не подведёт — этаж номер 10. f(1, m) = m
Возьмём второе яйцо, попыток опять 10. Теперь-то можно рискнуть с сотого? Разобьётся — останется ещё одно и 9 попыток, хотя бы 9 этажей получится пройти. Так может и рисковать нужно не с сотого, а с десятого? Логично. Тогда, в случае успеха, останется 2 яйца и 9 попыток. По аналогии, теперь нужно подняться ещё на 9 этажей. При серии успехов — ещё на 8, 7, 6, 5, 4, 3, 2 и 1. Итого, мы на 55-ом этаже с двумя целыми яйцами и без попыток. Ответом видится сумма первых M членов арифметической прогрессии с первым членом 1 и шагом 1. f(2, m) = (m*m + m) / 2. А ещё видно, что на каждом шаге как бы происходил вызов функции f(1, m), но это пока не точно.
Продолжим с тремя яйцами и десятью попытками. В случае неудачного первого броска, прикрыты снизу будут этажи, определяемые 2 яйцами и 9 попытками, а это значит, что первый бросок надо совершать с этажа f(2, 9) + 1. Тогда, в случае успеха, имеем 3 яйца и 9 попыток. И для второй попытки нужно подняться ещё на f(2,8) + 1 этажей. И так далее, пока на руках не останется 3 яйца и 3 попытки. И тут самое время отвлечься на рассмотрение случаев с N=M, когда яиц столько же, сколько и попыток.
А заодно и тех, когда яиц больше.
Но тут всё очевидно — нам не пригодятся яйца сверх тех, что разобьются, даже если каждый бросок будет неудачным. f(n, m) = f(m, m), если n > m. И вот всего поровну, 3 яйца, 3 броска. Если первое яйцо разбивается, то проверить можно f(2, 2) этажей к низу, а если не разбивается, то f(3,2) этажей к верху, то есть те же f(2, 2). Итого f(3, 3) = 2*f(2, 2) + 1 = 7. А f(4, 4), по аналогии, сложится из двух f(3, 3) и единицы, и будет равно 15. Всё это напоминает степени двойки, так и запишем: f(m, m) = 2^m — 1.
Выглядит, как бинарный поиск в физическом мире: начинаем с этажа номер 2^(m-1), в случае успеха поднимаемся на 2^(m-2) этажа вверх, а в случае неудачи — спускаемся на столько же вниз, и так, пока не кончатся попытки. В нашем случае, всё время поднимаемся.
Выглядит, как бинарный поиск в физическом мире: начинаем с этажа номер 2^(m-1), в случае успеха поднимаемся на 2^(m-2) этажа вверх, а в случае неудачи — спускаемся на столько же вниз, и так, пока не кончатся попытки. В нашем случае, всё время поднимаемся.
Вернёмся к f(3, 10). По сути, на каждом шаге всё сводится к сумме f(2, m-1) — количеству этажей, которые можно определить в случае неудачи, единицы и f(3, m-1) — количеству этажей, которые можно определить в случае успеха. И становится понятно, что от увеличения количества яиц и попыток вряд ли что-то изменится. f(n, m) = f(n — 1, m — 1) + 1 + f(n, m — 1). И это универсальная формула, можно воплощать в коде.
from functools import lru_cache
@lru_cache()
def height(n,m):
if n==0 or m==0: return 0
elif n==1: return m
elif n==2: return (m**2+m)/2
elif n>=m: return 2**n-1
else: return height(n-1,m-1)+1+height(n,m-1)Разумеется, предварительно я наступил на грабли немемоизирования рекурсивных функций и узнал, что f(10, 40) выполняется почти 40 секунд с количеством вызов самой себя — 97806983. Но и мемоизация спасает только на начальных интервалах. Если f(200,400) выполняется за 0.8 секунды, то f(200, 500) уже за 31 секунду. Забавно, что при замере времени выполнения с помощью %timeit, то результат получается куда меньше реального. Очевидно, что первый прогон функции занимает большую часть времени, а остальные просто пользуются результатами его мемоизации. Ложь, наглая ложь и статистика.
Рекурсия не нужна, ищем дальше
Итак, в тестах фигурирует, например, f(9477, 10000), а у меня жалкая f(200, 500) уже не укладывается в нужное время. Значит есть другое решение, без рекурсии, продолжим его поиски. Дополнил код подсчетом вызовов функции с определёнными параметрами, чтобы посмотреть на что она в итоге раскладывается. Для 10 попыток получились такие результаты:
f(3,10) = 7+ 1*f(2,9)+ 1*f(2,8)+ 1*f(2,7)+ 1*f(2,6)+ 1*f(2,5)+ 1*f(2,4)+ 1*f(2,3)+ 1*f(3,3)
f(4,10) = 27+ 1*f(2,8)+ 2*f(2,7)+ 3*f(2,6)+ 4*f(2,5)+ 5*f(2,4)+ 6*f(2,3)+ 6*f(3,3)+ 1*f(4,4)
f(5,10) = 55+ 1*f(2,7)+ 3*f(2,6)+ 6*f(2,5)+ 10*f(2,4)+ 15*f(2,3)+ 15*f(3,3)+ 5*f(4,4)+ 1*f(5,5)
f(6,10) = 69+ 1*f(2,6)+ 4*f(2,5)+ 10*f(2,4)+ 20*f(2,3)+ 20*f(3,3)+ 10*f(4,4)+ 4*f(5,5)+ 1*f(6,6)
f(7,10) = 55+ 1*f(2,5)+ 5*f(2,4)+ 15*f(2,3)+ 15*f(3,3)+ 10*f(4,4)+ 6*f(5,5)+ 3*f(6,6)+ 1*f(7,7)
f(8,10) = 27+ 1*f(2,4)+ 6*f(2,3)+ 6*f(3,3)+ 5*f(4,4)+ 4*f(5,5)+ 3*f(6,6)+ 2*f(7,7)+ 1*f(8,8)
f(9,10) = 7+ 1*f(2,3)+ 1*f(3,3)+ 1*f(4,4)+ 1*f(5,5)+ 1*f(6,6)+ 1*f(7,7)+ 1*f(8,8)+ 1*f(9,9)
Какая-то закономерность просматривается:

Коэффициенты эти теоретически рассчитываются. Каждый голубой — сумма верхнего и левого. А фиолетовые — те же самые голубые, только в обратном порядке. Рассчитать можно, но это же опять рекурсия, а в ней я разочаровался. Скорее всего, многие (жаль, что не я) уже узнали эти числа, но я пока сохраню интригу, следуя своему пути решения. Решил на них плюнуть и зайти с другой стороны.
Открыл эксель, соорудил табличку с результатами работы функции и стал высматривать закономерности. С3=ЕСЛИ(C$2>$B3;2^$B3-1;C2+B2+1), где $2 — строка с количеством яиц (1-13), $B — столбец с количеством попыток (1-20), C3 — ячейка на пересечении двух яиц и одной попытки.

Серая диагональ это N=M и тут наглядно видно, что справа от неё (при N > M) ничего не меняется. Видно — да иначе и быть не может, ведь это все результаты работы формулы, в которой так и задано- что каждая ячейка равна сумме верхней, верхней слева и единицы. Но какой-то универсальной формулы, куда можно подставить N и M и получить номер этажа, найти не удалось. Спойлер: её и не существует. Но зато так просто создание этой таблицы в экселе выглядит, может быть можно сгенерировать такую же питоном и таскать из неё ответы?
NumPy, вам нет
Вспоминаю, что существует NumPy, который как раз предназначен для работы с многомерными массивами, почему бы не попробовать его? Для начала нам понадобится одномерный массив из нулей размером в N+1 И одномерный массив из единиц размером в N. Берём первый массив от нулевого до предпоследнего элемента, складываем поэлементно с первым же массивом от первого элемента до последнего и с массивом единиц. К получившемуся массиву в начало добавляем ноль. Повторять M раз. Элемент номер N получившегося массива и будет ответом. Первые 3 шага выглядят так:

NumPy работает так быстро, что сохранять всю таблицу я не стал — каждый раз считал нужную строку заново. Одно но — результат работы на больших числах был неправильный. Старшие разряды вроде те, а младшие — нет. Так выглядят накопившиеся от многократного сложения погрешности арифметики чисел с плавающей точкой. Не беда — можно же изменить тип массива на int. Нет, беда — оказалось, что NumPy ради быстродействия работает только со своими типами данных, а его int, в отличие от питоновского int, может быть не больше 2^64-1, после чего молча переполняется и продолжается с -2^64. А у меня вообще-то ожидаются числа под три тысячи знаков. Зато работает очень быстро, f(9477, 10000) выполняется 233 мс, просто на выходе ерунда какая-то получается. Код даже приводить не буду, раз такое дело. Попробую сделать то же самое чистым питоном.
Итерировал, итерировал, да не выитерировал
def height(n, m):
arr = [0]*(n+1)
while m > 0:
arr = [0] + list(map(lambda x,y: x+y+1, arr[:-1], arr[1:]))
m-=1
return arr[n]44 секунды на расчет f(9477, 10000), многовато. Но зато абсолютно точно. Что можно оптимизировать? Первое — нет нужды считать всё, что правее диагонали M,M. Второе — ни к чему считать последний массив целиком, ради одной-то ячейки. Для этого сгодятся две последние две ячейки предыдущего. Для вычисления f(10, 20) будет достаточно только вот этих серых ячеек:

И так это выглядит в коде:
def height(n, m):
arr = [0, 1, 1]
i = 1
while i < n and i < m-n: # треугольник слева от m,m
arr = [0] + list(map(lambda x,y: x+y+1, arr[:-1], arr[1:]))
arr += [arr[-1]]
i+=1
arr.pop(-1)
while i < n or i < m-n: # прямоугольник или трапеция до начала следующего треугольника
arr = list(map(lambda x,y: x+y+1, arr[:-1], arr[1:]))
arr = arr + [arr[-1]+1] if n > len(arr) else [0] + arr
i+=1
while i < m: # треугольник, сходящийся в одну ячейку - ответ
arr = list(map(lambda x,y: x+y+1, arr[:-1], arr[1:]))
i+=1
return arr[0]И что вы думаете? f(9477, 10000) за 2 секунды! Но эти входные данные слишком хороши, длина массива на любом этапе будет не больше 533 элементов (10000-9477). Проверим на f(5477, 10000) — 11 секунд. Тоже хорошо, но только по сравнению с 44 секундами — двадцать тестов с таким временем не пройдёшь.
Всё не то. Но раз есть задача, значит есть и решение, поиски продолжаются. Я снова стал смотреть в экселевскую таблицу. Ячейка слева от (m, m) всегда на единицу меньше. А ячейка слева от неё уже нет, в каждой строке разность становится больше. Ячейка снизу от (m, m) всегда вдвое больше. А ячейка снизу от неё — уже не вдвое, а чуть меньше, но для каждого столбца по разному, чем дальше, тем больше. А ещё числа в одной строке сначала растут быстро, а после середины медленно. Дай-ка я построю таблицу разностей между соседними ячейками, может там какая закономерность появится?
Теплее

Ба, знакомые числа! То есть сумма N этих числе в строке номер M это и есть ответ? Правда, считать их — примерно то же самое, что я уже делал, вряд ли это сильно ускорит работу. Но надо попробовать:
f(9477, 10000): 17 секунд
def height(n, m):
arr = [1,1]
while m > 1:
arr = [1] + list(map(lambda x,y: x+y, arr[1:], arr[:-1])) + [1]
m-=1
return sum(arr[1:n+1])
Или 8, если считать только половину треугольника
def height(n, m):
arr = [1,1]
while m > 2 and len(arr) < n+2: # половина треугольника или трапеция, если n < половины
arr = [1] + list(map(lambda x,y: x+y, arr[1:], arr[:-1]))
arr = [1] + list(map(lambda x,y: x+y, arr[1:], arr[:-1]))
arr += [arr[-1]]
m-=2
while m > 1:
arr = [1] + list(map(lambda x,y: x+y, arr[1:], arr[:-1]))
m-=1
if len(arr) < n+1: arr += arr[::-1][1:] # если n во второй половине, отражаем строку
return sum(arr[1:n+1])
Не сказать, что более оптимальное решение. На каких-то данных работает быстрее, на каких-то медленнее. Надо отправляться глубже. Что это за треугольник с числами, что появился в решении дважды? Стыдно признаться, но высшую математику, где треугольник наверняка фигурировал, я благополучно позабыл, так что пришлось гуглить.
Бинго!
Треугольник Паскаля, так он официально называется. Бесконечная таблица биномиальных коэффициентов. Так что ответом на задачу с N яйцами и M бросками является сумма первых N коэффициентов в разложении бинома Ньютона M-ой степени, кроме нулевого.
Произвольный биномиальный коэффициент может быть вычислен через факториалы номера строки и номера коэффициента в строке: bk = m!/(n!*(m-n!)). Но самое приятное — можно последовательно рассчитать числа в строке, зная её номер и нулевой коэффициент (всегда единица): bk[n] = bk[n-1] * (m — n + 1) / n. На каждом шаге числитель уменьшается на единицу, а знаменатель увеличивается. И лаконичное финальное решение выглядит так:
def height(n, m):
h, bk = 0, 1 # высота и нулевой биномиальный коэффициент
for i in range(1, n + 1):
bk = bk * m // i
h += bk
m-=1
return h
33 мс. на расчёт f(9477, 10000)! Это решение тоже можно оптимизировать, хотя в заданных диапазонах и оно отлично работает. Если n лежит во второй половине треугольника, то можно инвертировать его в m-n, посчитать сумму первых n коэффициентов и отнять её от 2^m-2. Если n близко к середине и m нечётное, то расчеты тоже можно сократить: сумма первой половины строки будет равна 2^(m-1)-1, последний коэффициент в первой половине можно рассчитать через факториалы, его номер это (m-1)/2, а дальше либо продолжаем прибавлять коэффициенты, если n в правой половине треугольника, либо отнимать, если в левой. Если m чётное, то половину строки уже не посчитаешь, но можно найти сумму первых m/2+1 коэффициентов, посчитав через факториалы средний и прибавив половину его к 2^(m-1)-1. На входных данных в районе 10^6 это очень заметно уменьшает время выполнения.
Уже после успешного решения, стал искать чьи-нибудь ещё изыскания по этому вопросу, но нашёл только то самое, с собеседований, с всего лишь двумя яйцами, а это не спортивно. Интернет будет неполон без моего решения, решил я, и вот оно.