Я долго готовился и собирал материал, надеюсь в этот раз получилось лучше. Эту статью посвящаю основным методам решения задач математической оптимизации с ограничениями, так что если вы слышали, что симплекс-метод — это какой-то очень важный метод, но до сих пор не знаете, что он делает, то возможно эта статья вам поможет.
P. S. Статья содержит математические формулы, добавленные макросами хабраредактора. Говорят, что они иногда не отображаются. Также есть много анимаций в формате gif.
Задача математической оптимизации — это задача вида «Найти в множестве элемент
элемент  такой, что для всех
такой, что для всех  из
из  выполняется
выполняется  », что в научной литературе скорее будет записано как-то так
», что в научной литературе скорее будет записано как-то так
Исторически так сложилось, что популярные методы такие как градиентный спуск или метод Ньютона работают только в линейных пространствах (причем желательно простых, например ). На практике же часто встречаются задачи, где нужно найти минимум не в линейном пространстве. Например нужно найти минимум некоторой функции на таких векторах
). На практике же часто встречаются задачи, где нужно найти минимум не в линейном пространстве. Например нужно найти минимум некоторой функции на таких векторах  , для которых
, для которых  , это может быть обусловлено тем, что
, это может быть обусловлено тем, что  обозначают длины каких-либо объектов. Или же например, если
обозначают длины каких-либо объектов. Или же например, если  представляют координаты точки, которая должна быть на расстоянии не больше
представляют координаты точки, которая должна быть на расстоянии не больше  от
от  , т. е.
, т. е.  . Для таких задач градиентный спуск или метод Ньютона уже напрямую не применить. Оказалось, что очень большой класс задач оптимизации удобно покрывается «ограничениям», подобными тем, что я описал выше. Иначе говоря, удобно представлять множество
. Для таких задач градиентный спуск или метод Ньютона уже напрямую не применить. Оказалось, что очень большой класс задач оптимизации удобно покрывается «ограничениям», подобными тем, что я описал выше. Иначе говоря, удобно представлять множество  в виде системы равенств и неравенств
в виде системы равенств и неравенств
Задачи минимизации над пространством вида таким образом стали условно называть «задачами без ограничений» (unconstrained problem), а задачи над множествами, заданными наборами равенств и неравенств — «задачами с ограничениями» (constrained problem).
таким образом стали условно называть «задачами без ограничений» (unconstrained problem), а задачи над множествами, заданными наборами равенств и неравенств — «задачами с ограничениями» (constrained problem).
Технически, совершенно любое множество можно представить в виде одного равенства или неравенство с помощью индикатор-функции, которая определяется как
можно представить в виде одного равенства или неравенство с помощью индикатор-функции, которая определяется как
однако такая функция не обладает разными полезными свойствами (выпуклость, дифференцируемость и т. п.). Тем не менее, часто можно представить в виде нескольких равенств и неравенств, каждое из которых такими свойствами обладает. Основная теория подведена под случай
в виде нескольких равенств и неравенств, каждое из которых такими свойствами обладает. Основная теория подведена под случай
где — выпуклые (но не обязательно дифференцируемые) функции,
— выпуклые (но не обязательно дифференцируемые) функции,  — матрица. Для демонстрации работы методов я буду использовать два примера:
— матрица. Для демонстрации работы методов я буду использовать два примера:
Из всех методов, которые я покрываю этим обзором, симплекс-метод наверно является самым известным. Метод был разработан специально для линейного программирования и единственный из представленных достигает точного решения за конечное число шагов (при условии, что для вычислений используется точная арифметика, на практике это обычно не так, но в теории возможно). Идея симплекс-метода состоит из двух частей:
Симплекс-метод является итеративным, то есть он последовательно по чуть-чуть улучшает решение. Для таких методов нужно с чего-то начинать, в общем случае это делается с помощью решения вспомогательной задачи
Если для решения этой задачи такое, что
такое, что  , то выполняется
, то выполняется  , иначе исходная задача вообще задана на пустом множестве. Чтобы решить вспомогательную задачу, можно также использовать симплекс-метод, начальной же точкой можно взять
, иначе исходная задача вообще задана на пустом множестве. Чтобы решить вспомогательную задачу, можно также использовать симплекс-метод, начальной же точкой можно взять  с произвольным
с произвольным  . Нахождение начальной точки можно условно назвать первой фазой метода, нахождение решение исходной задачи можно условно назвать второй фазой метода.
. Нахождение начальной точки можно условно назвать первой фазой метода, нахождение решение исходной задачи можно условно назвать второй фазой метода.
Про градиентный спуск я недавно писал отдельную статью, в которой в том числе кратко описал и этот метод. Сейчас этот метод вполне себе живой, но изучается как часть более общего проксимального градиентного спуска. Сама идея метода совсем банальна: если мы применяем градиентный спуск к выпуклой функции , то при правильном выборе параметров получаем глобальный минимум
, то при правильном выборе параметров получаем глобальный минимум  . Если же после каждого шага градиентного спуска корректировать полученную точку, взяв вместо нее её проекцию на замкнутое выпуклое множество
. Если же после каждого шага градиентного спуска корректировать полученную точку, взяв вместо нее её проекцию на замкнутое выпуклое множество  , то в результате мы получим минимум функции
, то в результате мы получим минимум функции  на
на  . Ну или более формально, проективный градиентный спуск — это алгоритм, который последовательно вычисляет
. Ну или более формально, проективный градиентный спуск — это алгоритм, который последовательно вычисляет
где
Последнее равенство определяет стандартный оператор проекции на множество, по сути это функция, которая по точке вычисляет ближайшую к ней точку множества
вычисляет ближайшую к ней точку множества  . Роль расстояния здесь играет
. Роль расстояния здесь играет  , стоит отметить, что здесь можно использовать любую норму, тем не менее проекции с разными нормами могут отличаться!
, стоит отметить, что здесь можно использовать любую норму, тем не менее проекции с разными нормами могут отличаться!
На практике проективный градиентный спуск используется только в особых случаях. Основная его проблема состоит в том, что вычисление проекции может быть еще более сложной задачей, чем исходная, а её нужно вычислять много раз. Самый распространенный случай, для которого удобно применять проективный градиентный спуск — это «коробочные ограничения», которые имеют вид
В этом случае проекция вычисляется очень просто, по каждой координате получается
Применение проективного градиентного спуска для задач линейного программирования совершенно бессмысленно, тем не менее если это все-таки сделать, то выглядеть будет как-то так
А вот как выглядит траектория проективного градиентного спуска для второй задачи, если
и если
Этот метод примечателен тем, что является первым полиномиальным алгоритмом для задач линейного программирования, его можно считать многомерным обобщением метода бисекции. Я начну с более общего метода разделяющей гиперплоскости:
Для задач оптимизации построение «разделяющей гиперплоскости» основано на следующем неравенстве для выпуклых функций
Если зафиксировать , то для выпуклой функции
, то для выпуклой функции  полупространство
полупространство  содержит только точки со значением не меньше, чем в точке
содержит только точки со значением не меньше, чем в точке  , а значит их можно отсечь, так как эти точки не лучше, чем та, что мы уже нашли. Для задач с ограничениями можно аналогичным образом избавиться от точек, которые гарантированно нарушают какое-то из ограничений.
, а значит их можно отсечь, так как эти точки не лучше, чем та, что мы уже нашли. Для задач с ограничениями можно аналогичным образом избавиться от точек, которые гарантированно нарушают какое-то из ограничений.
Самый простой вариант метода разделяющей гиперплоскости — это просто отсекать полупространства без добавления каких-либо точек. В результате на каждом шаге у нас будет некий многогранник. Проблема этого метода в том, что количество граней многогранника скорее всего будет возрастать от шага к шагу. Более того, оно может расти экспоненциально.
Метод эллипсоидов собственно на каждом шаге хранит эллипсоид. Точнее, после проведения гиперплоскости строится эллипсоид минимального объема, который содержит одну из частей исходного. Этого получается добиться за счет добавления новых точек. Эллипсоид всегда можно задать положительно определенной матрицей и вектором (центром эллипсоида) следующим образом
Построение минимального по объему эллипсоида, содержащего пересечение полупространства и другого эллипсоида, можно осуществить с помощью в меру громоздких формул. К сожалению на практике этот метод оказался все еще на так хорош, как симплекс-метод или метод внутренней точки.
А вот собственно как он работает для
и для
Этот метод имеет долгую историю развития, одни из первых предпосылок появились примерно в то же время, когда был разработан симплекс-метод. Но в то время он был еще недостаточно эффективен, чтобы использоваться на практике. Позднее в 1984 был разработан вариант метода специально для линейного программирования, который был хорош как в теории, так и на практике. Более того, метод внутренней точки не ограничен только линейным программированием в отличие от симплекс-метода, и сейчас он является основным алгоритмом для задач выпуклой оптимизации с ограничениями.
Базовая идея метода — замена ограничений на штраф в виде так называемой барьерной функции. Функция называется барьерной функцией для множества
называется барьерной функцией для множества  , если
, если
Здесь — внутренность
— внутренность  ,
,  — граница
— граница  . Вместо исходной задачи предлагается решать задачу
. Вместо исходной задачи предлагается решать задачу
 и
и  заданы только на внутренности
заданы только на внутренности  (по сути отсюда и название), свойство барьера гарантирует, что у
(по сути отсюда и название), свойство барьера гарантирует, что у  минимум по
минимум по  существует. Более того, чем больше
существует. Более того, чем больше  , тем больше влияние
, тем больше влияние  . При достаточно разумных условиях можно добиться того, что если устремить
. При достаточно разумных условиях можно добиться того, что если устремить  к бесконечности, то минимум
к бесконечности, то минимум  будет сходиться к решению исходной задачи.
будет сходиться к решению исходной задачи.
Если множество задано в виде набора неравенств
задано в виде набора неравенств  , то стандартным выбором барьерной функции является логарифмический барьер
, то стандартным выбором барьерной функции является логарифмический барьер
Точки минимума функции
функции  для разных
для разных  образует кривую, которую обычно называют центральный путь, метод внутренний точки как бы пытается следовать этому пути. Вот так он выглядит для
образует кривую, которую обычно называют центральный путь, метод внутренний точки как бы пытается следовать этому пути. Вот так он выглядит для
Наконец сам метод внутренней точки имеет следующий вид
Использование метода Ньютона здесь очень важно: дело в том, что при правильном выборе барьерной функции шаг метода Ньютона генерирует точку,которая остается внутри нашего множества, поэкспериментировали, в таком виде не всегда выдает. Ну и наконец, так выглядит траектория метода внутренней точки

P. S. Статья содержит математические формулы, добавленные макросами хабраредактора. Говорят, что они иногда не отображаются. Также есть много анимаций в формате gif.
Преамбула
Задача математической оптимизации — это задача вида «Найти в множестве
Исторически так сложилось, что популярные методы такие как градиентный спуск или метод Ньютона работают только в линейных пространствах (причем желательно простых, например
Задачи минимизации над пространством вида
Технически, совершенно любое множество
однако такая функция не обладает разными полезными свойствами (выпуклость, дифференцируемость и т. п.). Тем не менее, часто можно представить
где
- Задача линейного программирования
По сути эта задача состоит в том, чтобы найти самую дальнюю точку многоугольника в направлении (2, 1), решение задачи — точка (4.7, 3.5) — самая «правая» в многоугольнике). А вот собственно и сам многоугольник

- Минимизация квадратичной функции с одним квадратичным ограничением
Симплекс-метод
Из всех методов, которые я покрываю этим обзором, симплекс-метод наверно является самым известным. Метод был разработан специально для линейного программирования и единственный из представленных достигает точного решения за конечное число шагов (при условии, что для вычислений используется точная арифметика, на практике это обычно не так, но в теории возможно). Идея симплекс-метода состоит из двух частей:
- Системы линейных неравенств и равенств задают многомерные выпуклые многогранники (политопы). В одномерном случае это точка, луч или отрезок, в двумерном — выпуклый многоугольник, в трехмерном — выпуклый многогранник. Минимизация линейной функции — это по сути нахождение самой «дальней» точки в определенном направлении. Думаю, интуиция должна подсказывать, что этой самой дальней точкой должна быть некая вершина, и это действительно так. В общем случае, для системы из
неравенств в
-мерном пространстве вершина — это точка, удовлетворяющая системе, для которой ровно
из этих неравенств обращаются в равенства (при условии, что среди неравенств нет эквивалентных). Таких точек всегда конечное число, хоть их и может быть очень много.
- Теперь у нас есть конечный набор точек, вообще говоря можно их просто взять и перебрать, то есть сделать что-то такое: для каждого подмножества из
неравенств решить систему линейных уравнений, составленных на выбранных неравенствах, проверить, что решение подходит в исходную систему неравенств и сравнить с другими такими точками. Это довольно простой неэффективный, но рабочий метод. Симплекс-метод вместо перебора двигается от вершины к вершине по ребрам таким образом, чтобы значений целевой функции улучшалось. Оказывается, если у вершины нет «соседей», в которых значений функции лучше, то она оптимальна.
Симплекс-метод является итеративным, то есть он последовательно по чуть-чуть улучшает решение. Для таких методов нужно с чего-то начинать, в общем случае это делается с помощью решения вспомогательной задачи
Если для решения этой задачи
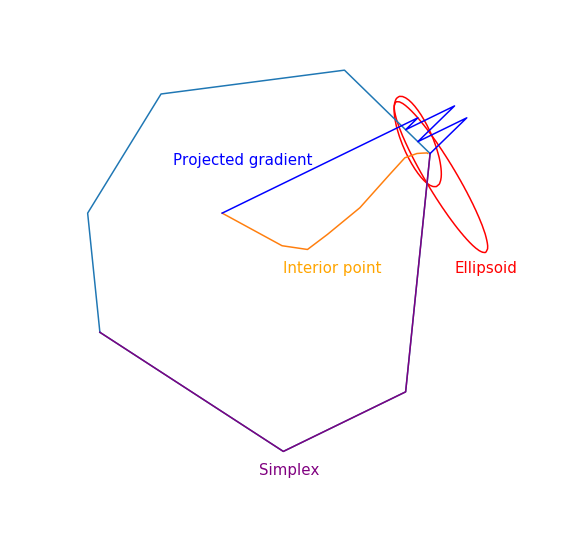
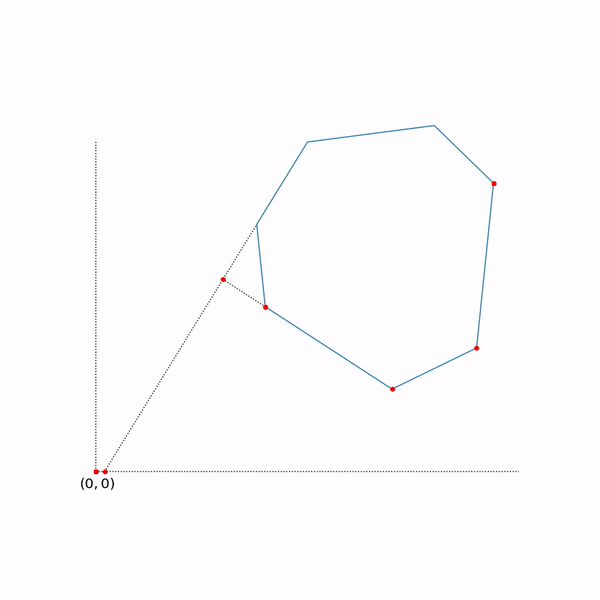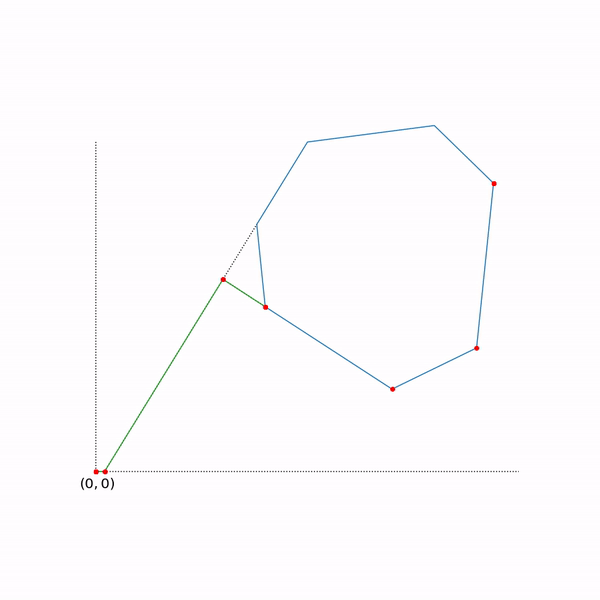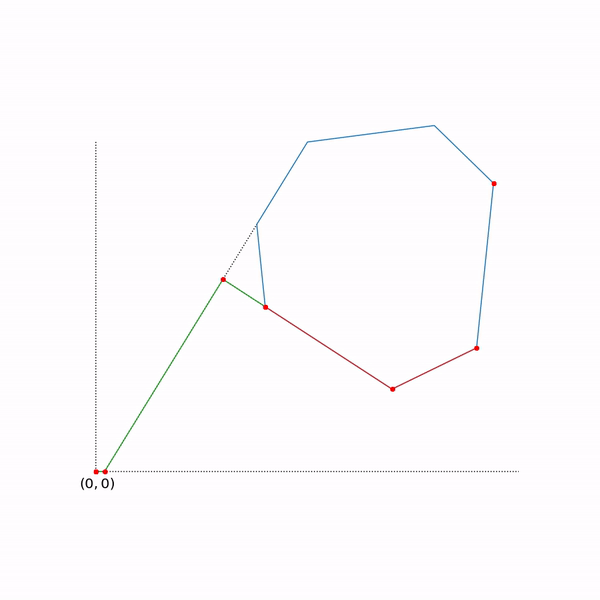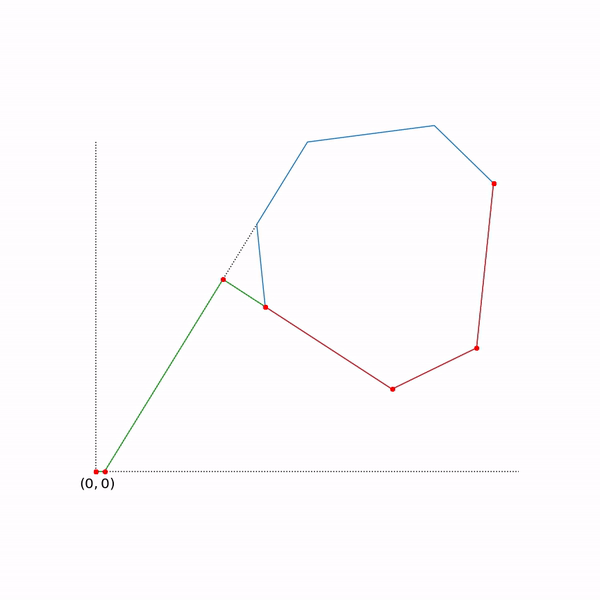
Траектория двухфазового симплекс-метода
Траектория была сгенерирована с помощью scipy.optimize.linprog.

Проективный градиентный спуск
Про градиентный спуск я недавно писал отдельную статью, в которой в том числе кратко описал и этот метод. Сейчас этот метод вполне себе живой, но изучается как часть более общего проксимального градиентного спуска. Сама идея метода совсем банальна: если мы применяем градиентный спуск к выпуклой функции
где
Последнее равенство определяет стандартный оператор проекции на множество, по сути это функция, которая по точке
На практике проективный градиентный спуск используется только в особых случаях. Основная его проблема состоит в том, что вычисление проекции может быть еще более сложной задачей, чем исходная, а её нужно вычислять много раз. Самый распространенный случай, для которого удобно применять проективный градиентный спуск — это «коробочные ограничения», которые имеют вид
В этом случае проекция вычисляется очень просто, по каждой координате получается
Применение проективного градиентного спуска для задач линейного программирования совершенно бессмысленно, тем не менее если это все-таки сделать, то выглядеть будет как-то так
Траектория проективного градиентного спуска для задачи линейного программирования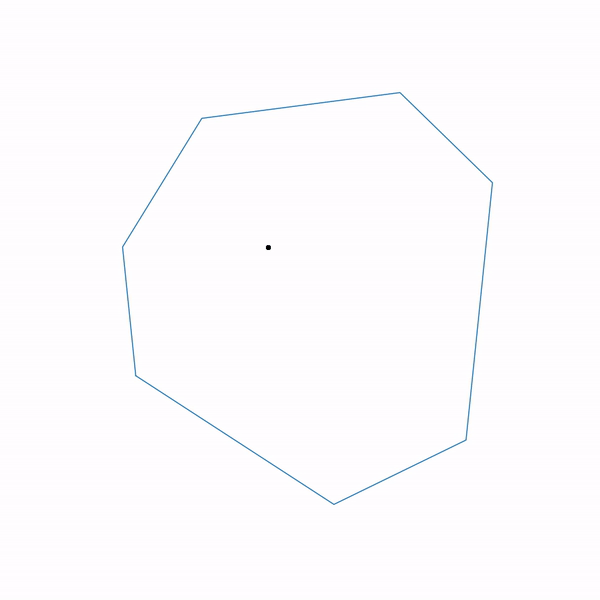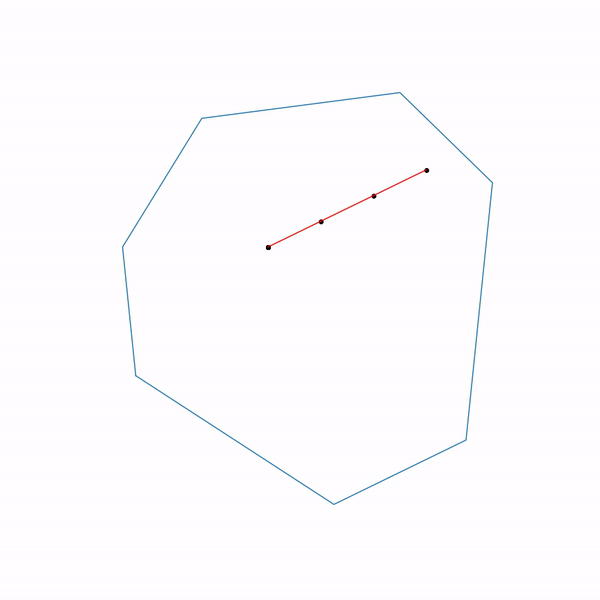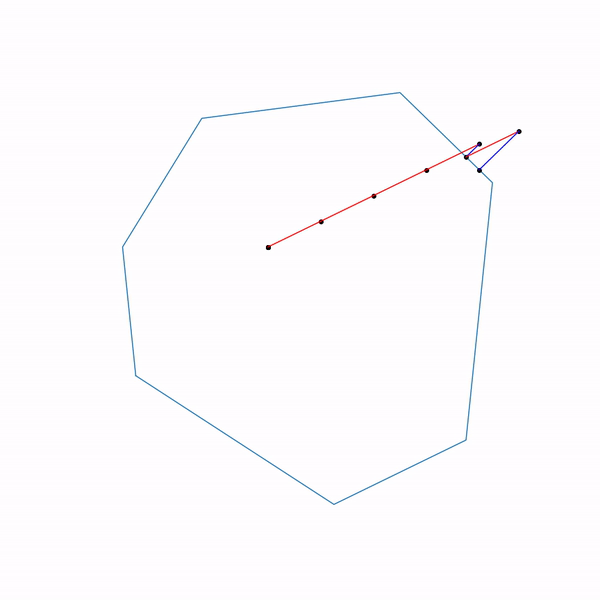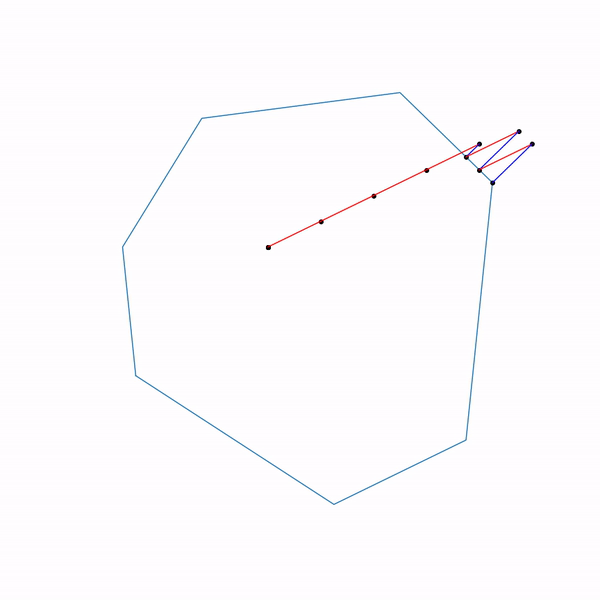

А вот как выглядит траектория проективного градиентного спуска для второй задачи, если
выбирать большой размер шага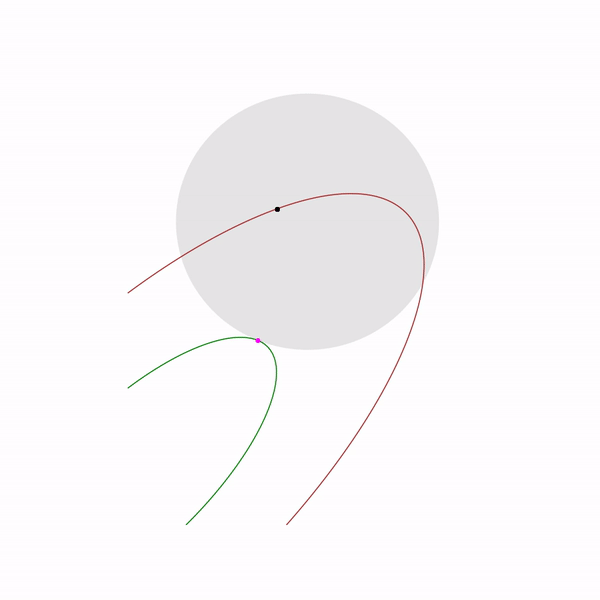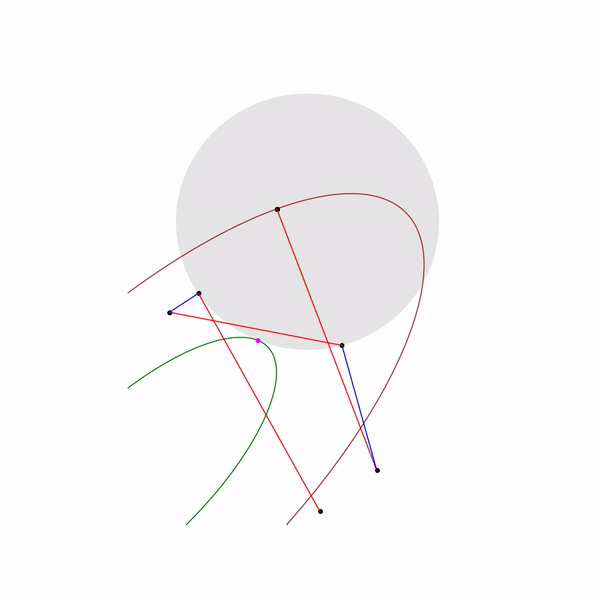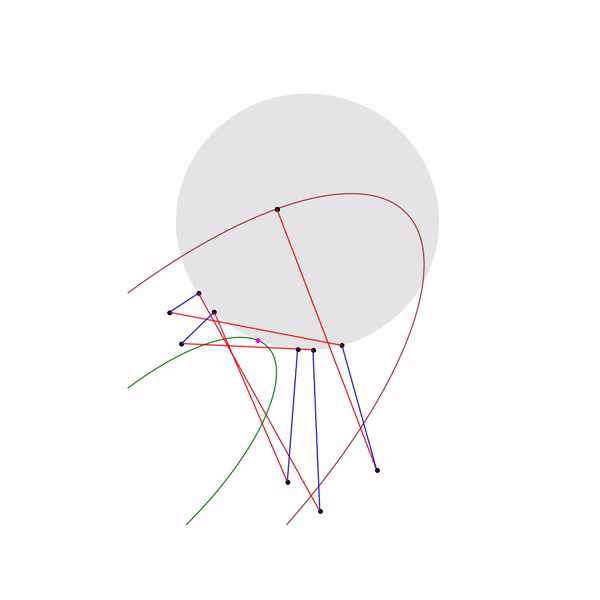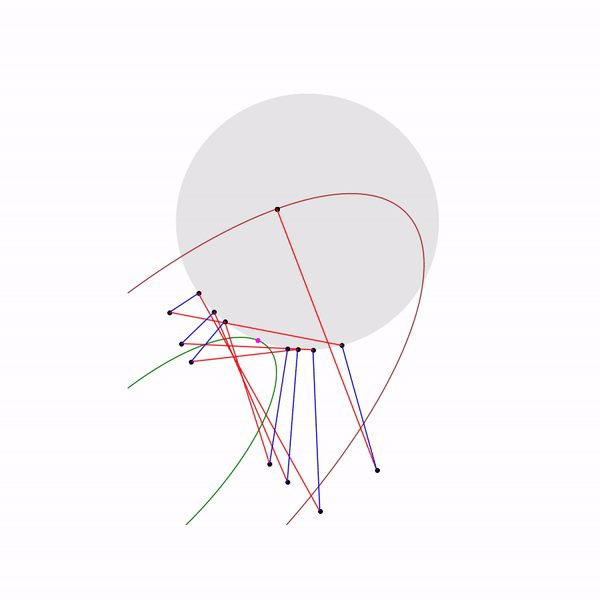

и если
выбирать небольшой размер шага

Метод эллипсоидов
Этот метод примечателен тем, что является первым полиномиальным алгоритмом для задач линейного программирования, его можно считать многомерным обобщением метода бисекции. Я начну с более общего метода разделяющей гиперплоскости:
- На каждом шаге метода есть некоторое множество, которое содержит решение задачи.
- На каждом шаге строится гиперплоскость, после чего из множества удаляются все точки, лежащие по одну сторону выбранной гиперплоскости, и, возможно, к этому множеству добавятся какие-то новые точки
Для задач оптимизации построение «разделяющей гиперплоскости» основано на следующем неравенстве для выпуклых функций
Если зафиксировать
Самый простой вариант метода разделяющей гиперплоскости — это просто отсекать полупространства без добавления каких-либо точек. В результате на каждом шаге у нас будет некий многогранник. Проблема этого метода в том, что количество граней многогранника скорее всего будет возрастать от шага к шагу. Более того, оно может расти экспоненциально.
Метод эллипсоидов собственно на каждом шаге хранит эллипсоид. Точнее, после проведения гиперплоскости строится эллипсоид минимального объема, который содержит одну из частей исходного. Этого получается добиться за счет добавления новых точек. Эллипсоид всегда можно задать положительно определенной матрицей и вектором (центром эллипсоида) следующим образом
Построение минимального по объему эллипсоида, содержащего пересечение полупространства и другого эллипсоида, можно осуществить с помощью в меру громоздких формул. К сожалению на практике этот метод оказался все еще на так хорош, как симплекс-метод или метод внутренней точки.
А вот собственно как он работает для
линейного программирования

и для
квадратичного программирования

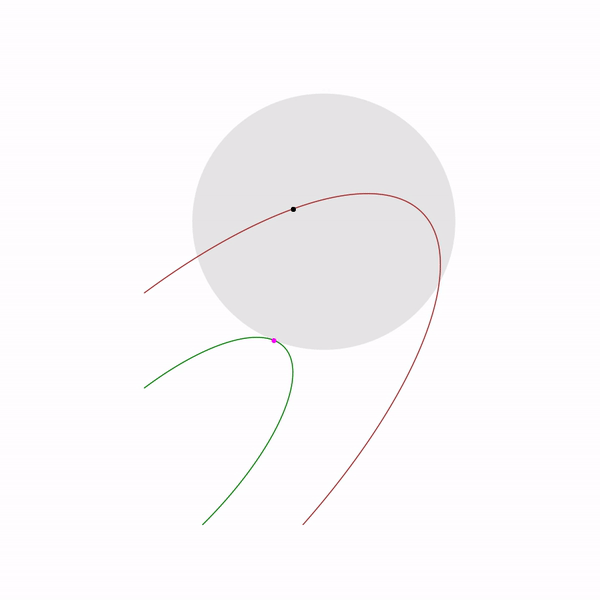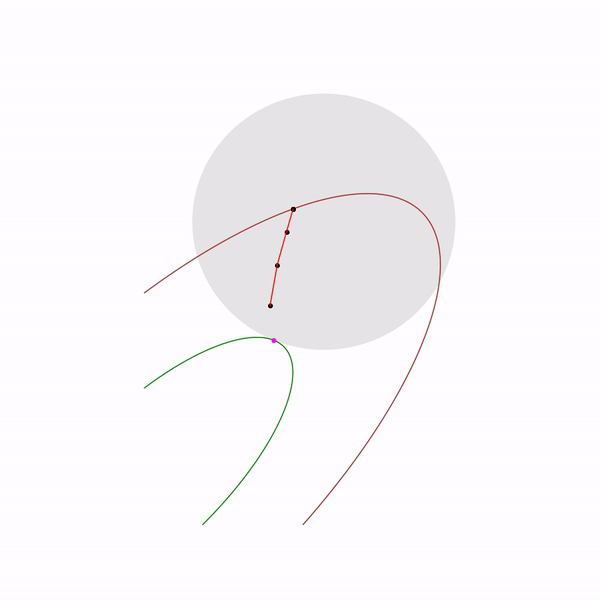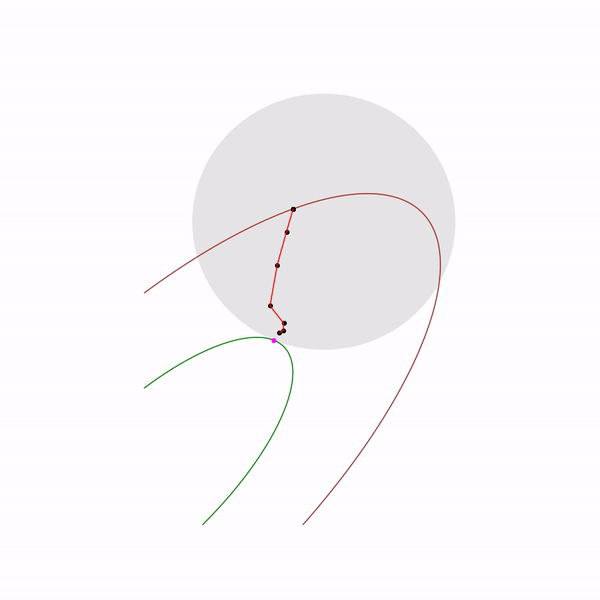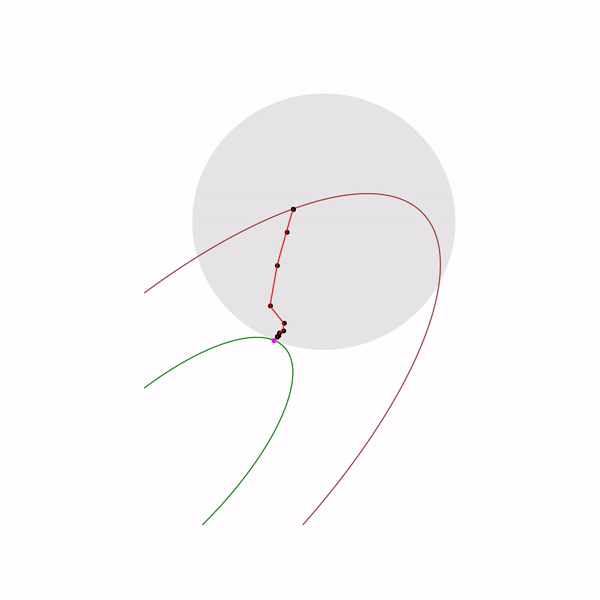
Метод внутренней точки
Этот метод имеет долгую историю развития, одни из первых предпосылок появились примерно в то же время, когда был разработан симплекс-метод. Но в то время он был еще недостаточно эффективен, чтобы использоваться на практике. Позднее в 1984 был разработан вариант метода специально для линейного программирования, который был хорош как в теории, так и на практике. Более того, метод внутренней точки не ограничен только линейным программированием в отличие от симплекс-метода, и сейчас он является основным алгоритмом для задач выпуклой оптимизации с ограничениями.
Базовая идея метода — замена ограничений на штраф в виде так называемой барьерной функции. Функция
Здесь
Если множество
Точки минимума
Примера с линейным программированием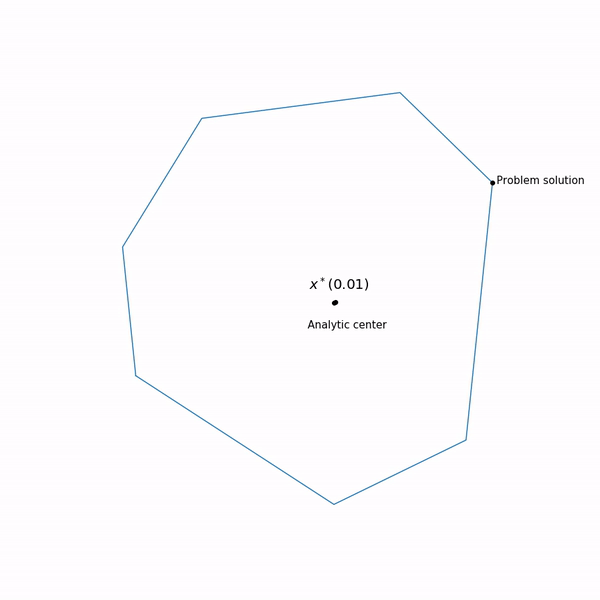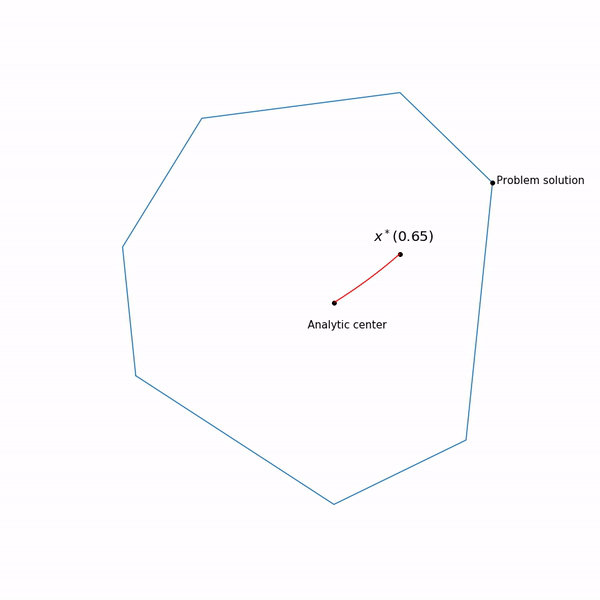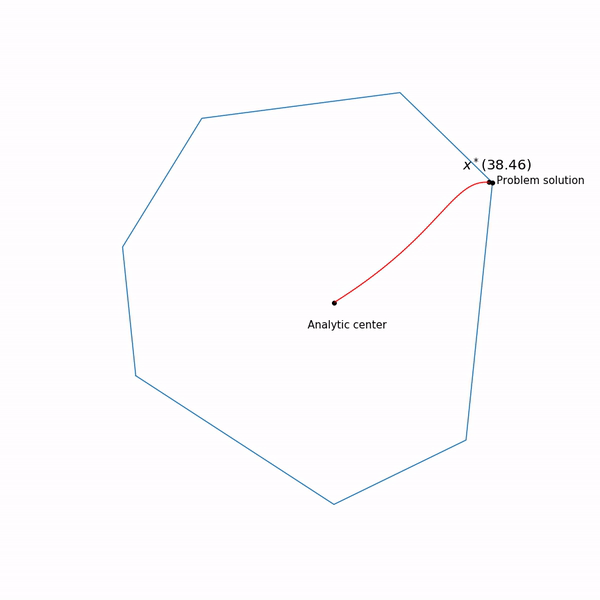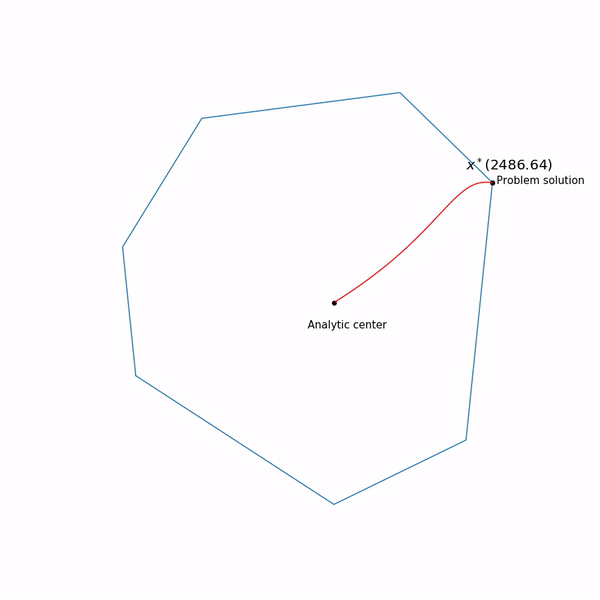
Аналитический центр — это просто

Аналитический центр — это просто
Наконец сам метод внутренней точки имеет следующий вид
- Выбрать начальное приближение
,
- Выбрать новое приближение методом Ньютона
- Увеличить
Использование метода Ньютона здесь очень важно: дело в том, что при правильном выборе барьерной функции шаг метода Ньютона генерирует точку,
Задача линейного программирования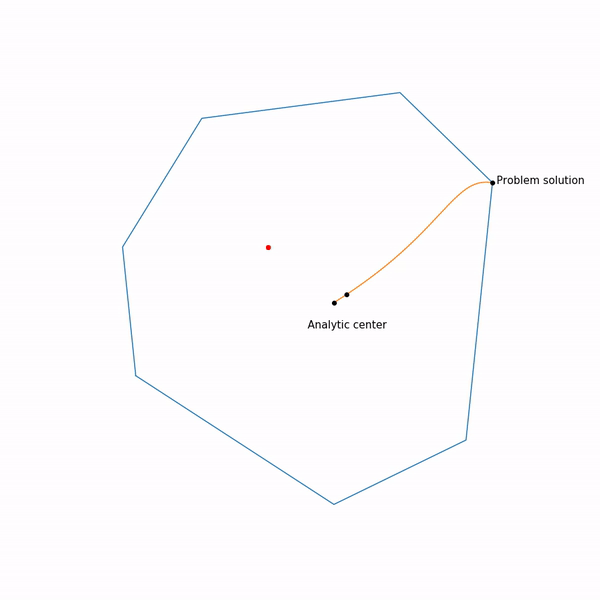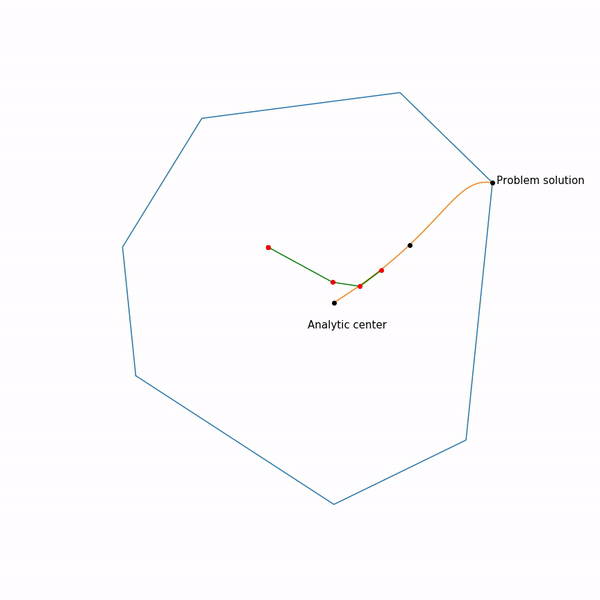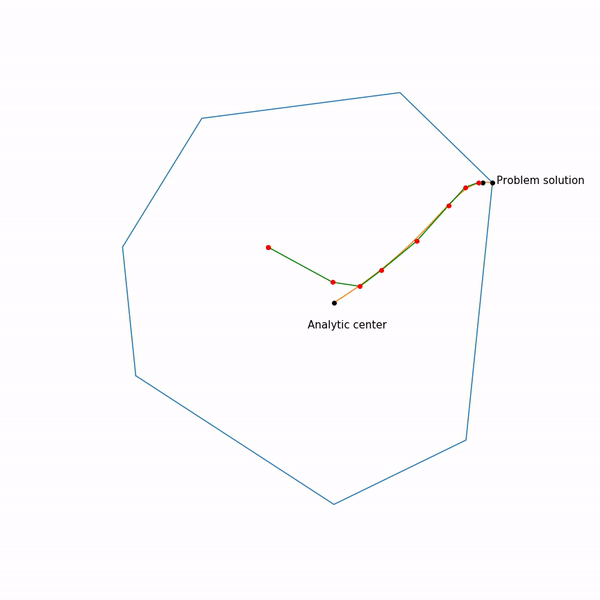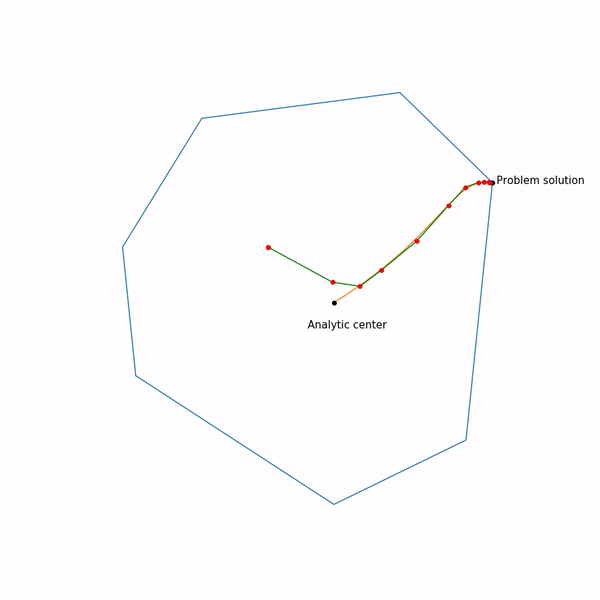
Прыгающая черная точка — это , т.е. точка, к которой мы пытаемся приблизиться шагом метода Ньютона на текущем шаге.
, т.е. точка, к которой мы пытаемся приблизиться шагом метода Ньютона на текущем шаге.

Прыгающая черная точка — это
Задача квадратичного программирования