PatientZero Nov 16 2018 at 11:12

Давайте уберём кватернионы из всех 3D-движков

13 min

30K

Working with 3D-graphics *Game development *Mathematics *

Translation

Для записи трёхмерных поворотов программисты графики используют кватернионы. Однако в кватернионах сложно разобраться, потому что изучают их поверхностно. Мы просто принимаем на веру странные таблицы умножения и другие загадочные определения, и используем их как «чёрные ящики», поворачивающие векторы так, как нам нужно. Почему $\mathbf{i}^2=\mathbf{j}^2=\mathbf{k}^2=-1$ и $\mathbf{i} \mathbf{j} = \mathbf{k}$ ? Почему мы берём вектор и превращаем его в «мнимый» вектор, чтобы преобразовать его, например $\mathbf{q} (x\mathbf{i} + y\mathbf{j} + z \mathbf{k}) \mathbf{q}^{*}$ ? Да кому это интересно, если всё работает, правда?

Существует способ описания поворотов под названием ротор, который относится к области и комплексных чисел (в 2D), и кватернионов (в 3D), и даже обобщается до любого количества измерений.

Мы можем создавать роторы практически полностью с нуля, вместо того, чтобы определять из ничего кватернионы и пытаться объяснить, как они работают задним числом. Это занимает больше времени, но мне кажется, что это стоит того, потому что их гораздо легче понять!

Кроме того, для визуализации и понимания трёхмерных роторов не нужно использовать четвёртое пространственное измерение.

Было бы здорово, если бы начали вытеснять использование и изучение кватернионов, заменяя их роторами. Заменить их очень просто, а код останется почти таким же. Всё, что можно делать с кватернионами, например, интерполяцию и устранение блокировки осей (Gimbal lock), можно сделать и с роторами. Но понимать мы начинаем гораздо больше.

(В оригинале статьи все графики интерактивны, а за статьёй следует видео. Нажимая на кнопки воспроизведения, можно запустить соответствующий раздел видео. Также можно нажать под видео кнопку перехода, чтобы перейти к соответствующему разделу статьи. Можно развернуть окно, чтобы для видео было больше места, или установить для него постоянный размер.)

1. Плоскости поворотов

1.1. Повороты выполняются на двухмерных плоскостях

В трёхмерном пространстве мы обычно воспринимаем повороты как происходящие вокруг осей, как колесо вращается на оси, но вместо этого корректнее будет представлять плоскость, на которой лежит колесо. Эта плоскость перпендикулярна оси.

Эта старушка крутит колесо в плоскости $\mathbf{xz}$ , перпендикулярно оси $\mathbf{y}$ .

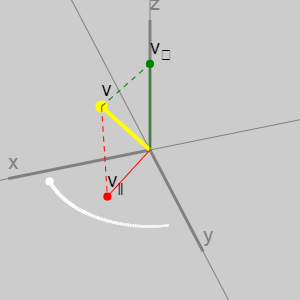
Так получается, потому что если мы разделили вектор на две части, одна из которых лежит на плоскости ( $\mathbf{v}_\parallel$ ), а другая находится за её пределами ( $\mathbf{v}_\perp$ ), то поворот вращает внутреннюю часть, а внешняя остаётся неизменной.

Поворот в плоскости $inline$ [в оригинале статьи это анимация и камеру можно перемещать]

В двухмерном пространстве есть только одна плоскость, в которой возможен поворот (внешней части нет). Поэтому считать, что повороты происходят вокруг третьей оси (перпендикулярной к 2D-плоскости) строго говоря неверно, потому что для выполнения поворотов мы не должны добавлять ещё одно измерение.

Если рассказать двухмерному «плоскоземельщику» (который живёт внутри 2D-плоскости и никогда не выбирался из двухмерного пространства) о перпендикулярной оси поворота, то он бы спросил: «В каком направлении указывает эта ось? Я не могу её представить!»

Примечание

И в более высоких измерениях (4D и выше) невозможно определить один вектор нормали к 2D-плоскости (например, в 4D у 2D-плоскости есть два направления нормалей, в 5D есть три направления нормалей, а в $inline$ их $inline$ )

1.2. Точное направление поворотов

Кроме того, когда мы думаем о повороте вокруг оси, направление поворота не определено, и поэтому его нужно определять по правилу (так называемому «правилу правой руки»).

Однако если считать, что повороты происходят внутри плоскостей, то направление становится понятным: поворот в плоскости $\mathbf{xy}$ означает поворот, который перемещает (единичный) вектор $\mathbf{x}$ к (единичному) вектору $\mathbf{y}$ внутри плоскости, которую они совместно образуют. Поворот в плоскости $\mathbf{yx}$ — это поворот в обратном направлении: он перемещает вектор $\mathbf{y}$ к вектору $\mathbf{x}$ .

Примечание

Помню, что когда я впервые узнал о трёх матрицах 3D-поворотов вдоль ортогональных плоскостей, то первым делом подумал: какого чёрта матрица $\mathbf{R_y}$ имеет противоположный знак? Так получается из-за правила правой руки, по которому мы должны определять поворот вокруг оси $\mathbf{y}$ так, чтобы он выполнялся от $\mathbf{z}$ к $\mathbf{x}$ , а не от $\mathbf{x}$ к $\mathbf{z}$ , чтобы сохранять постоянное «праворукое» направление поворота. Когда мы начинаем говорить непосредственно о самой плоскости, это правило становится ненужным.

$R_X(\theta) = \begin{bmatrix}1 & 0 & 0\\0 & cos(\theta) & -sin(\theta)\\0 & sin(\theta) & cos(\theta)\end{bmatrix} \: \: \: R_Y(\theta) = \begin{bmatrix}cos(\theta) & 0 & \bbox[5px,border-bottom:2px solid red]{\ \ }sin(\theta)\\0 & 1 & 0\\ \bbox[5px,border-bottom:2px solid red]{-}sin(\theta) & 0 & cos(\theta)\end{bmatrix} \: \: \: R_Z(\theta) = \begin{bmatrix}cos(\theta) & -sin(\theta) & 0\\sin(\theta) & cos(\theta) & 0\\0 & 0 & 1\end{bmatrix}$

2. Бивекторы

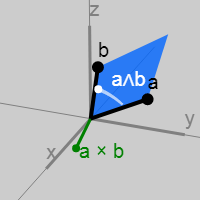
2.1. Внешнее произведение

Для вычисления оси поворота при повороте одного вектора $\mathbf{a}$ к другому вектору $\mathbf{b}$ мы берём векторное произведение двух векторов, чтобы получить вектор, перпендикулярный им обоим. Но зачем нам «уходить» из плоскости, если поворот по сути своей является двухмерной операцией?

Вместо этого мы возьмём то, что называется внешним произведением (также известное как двухмерное векторное произведение), двух векторов, создав новый элемент под названием «бивектор» (или 2-вектор) $\mathbf{B}$ , представляющий плоскость, которую совместно образуют два вектора. Если векторное произведение создаёт вектор нормали к плоскости, то внешнее произведение создаёт саму плоскость. Вычисление нормали к плоскости не относится к делу.

$\mathbf{B} = \mathbf{a} \wedge \mathbf{b}$

$\mathbf{B}$ можно представить как параллелограмм, построенный из векторов $\mathbf{a}$ и $\mathbf{b}$ в плоскости, которую они совместно образуют.

Поначалу идея бивектора может казаться странной, но скоро мы увидим, что они почти столь же фундаментальны, как и сами векторы. Если вектор можно сравнить с прямой, то бивектор подобен плоскости… Свойства внешнего произведения ухватывают важные свойства плоскостей.

2.2. Базис для бивекторов

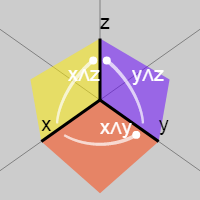
Бивекторы, как и векторы, имеют компоненты. Но они определяются на базисе плоскостей, а не прямых, как векторы.

Три ортогональных базисных плоскости — это $\mathbf{x} \wedge \mathbf{y}$ , $\mathbf{x} \wedge \mathbf{z}$ и $\mathbf{y} \wedge \mathbf{z}$ , как мы видим из рисунка.

Но сначала давайте рассмотрим более простой двухмерный случай…

2.3. Двухмерные бивекторы

В 2D есть только одна плоскость, а именно $\mathbf{xy}$ . То есть двухмерный бивектор имеет только один компонент. Для бивектора, составленного из векторов $\mathbf{a}$ и $\mathbf{b}$ , это число $B_{xy}$ равно площади (со знаком) параллелограмма, образованного двумя векторами.

$\mathbf{B}=\mathbf{a} \wedge \mathbf{b} = B_{xy} (\mathbf{x} \wedge \mathbf{y})$

В оригинале статьи с 2D-бивектором можно поэкспериментировать на интерактивном графике, изменяя (единичные) векторы, из которых он составлен:

Можно увидеть, что при изменении угла между векторами площадь параллелограмма меняется (в соответствии с синусом угла).

Если векторы совпадают или параллельны, то они не образуют правильной плоскости и результат будет равен нулю. Это простое свойство определяет то, чем является бивектор:

$\mathbf{a} \wedge \mathbf{a} = 0$

Взглянув на сумму двух векторов, можно увидеть, что из свойства следует:

$\begin{eqnarray}(\mathbf{a}+\mathbf{b}) \wedge (\mathbf{a}+\mathbf{b}) &=& 0 \\ \mathbf{a} \wedge \mathbf{a} + \mathbf{b} \wedge \mathbf{a} + \mathbf{a} \wedge \mathbf{b} + \mathbf{b} \wedge \mathbf{b} &=& 0 \\ \mathbf{b} \wedge \mathbf{a} + \mathbf{a} \wedge \mathbf{b} &=& 0 \end{eqnarray}$

Следовательно:

$\mathbf{a} \wedge \mathbf{b} = -\mathbf{b} \wedge \mathbf{a}$

Так же, как направление поворота, важен порядок аргументов во внешнем произведении. Перемена мест аргументов меняет знак результата (это называется «антисимметрией»).

На графике знак обозначается цветом, который сменяется с синего на зелёный. Знак меняется, когда поворот из $\mathbf{a}$ в $\mathbf{b}$ переходит от движения по часовой стрелке к движению против часовой стрелки (т.е. если он соответствует направлению (от $\mathbf{x}$ к $\mathbf{y}$ ) или направлению (от $\mathbf{y}$ к $\mathbf{x}$ )).

Можно увидеть, что свойства внешнего произведения устроены так, что передают свойства плоскостей и поворотов.

2.4. Двухмерные бивекторы из неединичных векторов

Очевидно, что векторы не обязаны быть единичной длины, и на этом графике данное ограничение устранено:

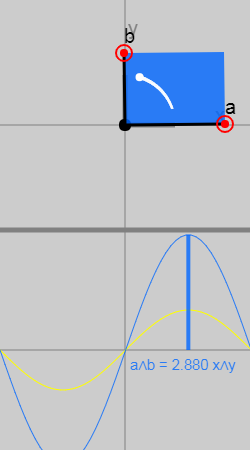
Площадь параллелограмма со знаком пропорциональна длинам обоих векторов: $B_{xy} = sin(\alpha)\|a\|\|b\|$ , где $\alpha$ — это угол между $\mathbf{a}$ и $\mathbf{b}$ . То есть, например, при удвоении длины одного вектора вдвое увеличивается площадь.

Мы можем получить истинное значение, подставив векторы в виде компонентов:

$\begin{eqnarray}\mathbf{a} \wedge \mathbf{b} &=& (a_x \mathbf{x} + a_y \mathbf{y}) \wedge (b_x \mathbf{x} + b_y \mathbf{y}) \\ &=& a_x b_x (\mathbf{x} \wedge \mathbf{x}) + a_x b_y (\mathbf{x} \wedge \mathbf{y}) + a_y b_x (\mathbf{y} \wedge \mathbf{x}) + a_y b_y (\mathbf{y} \wedge \mathbf{y}) \\ &=& a_x b_y (\mathbf{x} \wedge \mathbf{y}) + a_y b_x (\mathbf{y} \wedge \mathbf{x}) \\ &=& a_x b_y (\mathbf{x} \wedge \mathbf{y}) - a_y b_x (\mathbf{x} \wedge \mathbf{y}) \\ &=& (a_x b_y - a_y b_x) (\mathbf{x} \wedge \mathbf{y}) \end{eqnarray}$

$B_{xy} = a_x b_y - b_x a_y$

2.5. Трёхмерные бивекторы

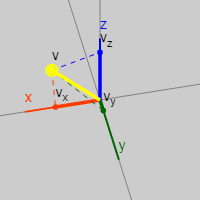
Так же, как координаты вектора $\mathbf{v}$ можно считать проекциями вектора на три ортогональных базисных оси ( $\mathbf{x}$ , $\mathbf{y}$ , $\mathbf{z}$ ), координаты бивектора $\mathbf{B}$ можно считать проекциями меньше плоскости на три ортогональные базисные плоскости.

Проекции вектора являются длинами этого вектора вдоль каждого базисного вектора, а проекции бивектора являются площадями плоскости на каждую базисную плоскость.

Для вектора:

$\mathbf{v} = \bbox[5px,border-bottom:2px solid red]{v_x} \mathbf{x} + \bbox[5px,border-bottom:2px solid green]{v_y} \mathbf{y} + \bbox[5px,border-bottom:2px solid blue]{v_z} \mathbf{z}$

Для бивектора:

$\mathbf{B} = \bbox[5px,border-bottom:2px solid coral]{B_{xy}} (\mathbf{x} \wedge \mathbf{y}) + \bbox[5px,border-bottom:2px solid gold]{B_{xz}} (\mathbf{x} \wedge \mathbf{z}) + \bbox[5px,border-bottom:2px solid DarkViolet]{B_{yz}} (\mathbf{y} \wedge \mathbf{z})$

Где $B_{xy}$ , $B_{xz}$ , $B_{yz}$ — это просто числа, наподобие $inline$ , $inline$ , $inline$ (они подчёркнуты цветами, соответствующими цветам на графике).

Компоненты 3D-бивектора — это просто три 2D-проекции бивектора на базисные 2D-плоскости.

Пользуясь тем же методом, что и раньше, мы находим, что истинные величины компонентов выглядят во многом похоже на компонент XY из двухмерного случая, но применённого ко всем трём плоскостям:

$B_{xy} = a_x b_y - b_x a_y$

$B_{xz} = a_x b_z - b_x a_z$

$B_{yz} = a_y b_z - b_y a_z$

Можно поэкспериментировать с 3D-бивектором на интерактивном графике в оригинале статьи:

Примечание

Норма бивектора $\|\mathbf{B}\|=\|\mathbf{a} \wedge \mathbf{b}\|$ определяется аналогично норме вектора (квадратный корень из суммы квадратов компонентов). Это равно площади параллелограмма, образованного $\mathbf{a}$ и $\mathbf{b}$ , т.е. $\|\mathbf{a} \wedge \mathbf{b}\|= \mid sin(\alpha)\mid\|\mathbf{a}\|\|\mathbf{b}\|$ , где $\alpha$ — угол между $\mathbf{a}$ и $\mathbf{b}$ .

Если мы разделим бивектор на его норму, то сократим две длины векторов и (абсолютное) значение синуса угла, то есть у нас останется бивектор $\hat{\mathbf{B}}$ , который будет построен так, как будто два вектора изначально были перпендикулярны и имели единичную длину. Это очень чистое представление плоскости, содержащей оба вектора. Значит:

$\mathbf{B} = |\mathbf{a}\|\|\mathbf{b}\| \mid sin(\alpha) \mid \hat{\mathbf{B}}$

Напоминает ли вам что-нибудь внешнее произведение? В 3D определение внешнего произведения очень схоже с определением векторного произведения. На самом деле, вектор в 3D, получаемый из векторного произведения (например, вектор нормали) будет иметь три компонента, равные компонентам бивектора (числа будут теми же, но базис отличается).

$\begin{eqnarray}\mathbf{a} \wedge \mathbf{b} &=& & (a_x b_y - b_x a_y)(\mathbf{x} \wedge \mathbf{y}) \\ & & + & (a_x b_z - b_x a_z)(\mathbf{x} \wedge \mathbf{z}) \\ & & + & (a_y b_z - b_y a_z)(\mathbf{y} \wedge \mathbf{z}) \\ \\ \mathbf{a} \times \mathbf{b} &=& & (a_x b_y - b_x a_y) \ \mathbf{z} \\ & & - & (a_x b_z - b_x a_z) \ \mathbf{y} \\ & & + & (a_y b_z - b_y a_z) \ \mathbf{x}\end{eqnarray}$

Определение бивектора имеет геометрический смысл, а не появляется из ниоткуда. Помню, что когда изучал векторные произведения, я думал: «Какого чёрта оно возвращает вектор, длина которого равна площади параллелограмма, образованного этими двумя векторами? Это кажется таким случайным. И почему нам можно превратить площадь параллелограмма в длину вектора?»

2.6. Семантика векторов и бивекторов

В 3D бивектор имеет три координаты, по одной на плоскость: ( $\mathbf{xy}$ , $\mathbf{xz}$ и $\mathbf{yz}$ ). Векторы также имеют три координаты, по одной на ось ( $\mathbf{x}$ , $\mathbf{y}$ и $\mathbf{z}$ ). Каждая плоскость перпендикулярна к одной оси. Это совпадение возникает только в трёх измерениях (*) и именно поэтому мы постоянно путаем бивекторы с векторами.

(*)

В 2D есть только один базисный бивектор ( $\mathbf{xy}$ ), а в 3D есть 3 базисных бивектора ( $\mathbf{xy}$ , $\mathbf{xz}$ , $\mathbf{yz}$ ), в 4D есть 6 базисных бивектора ( $\mathbf{xy}$ , $\mathbf{xz}$ , $\mathbf{xw}$ , $\mathbf{yz}$ , $\mathbf{yw}$ , $\mathbf{zw}$ ) и так далее...

В программировании они оба имеют одинаковую схему размещения в памяти, но разные операции. Использование 3D-вектора вместо 3D-бивектора похоже на «преобразование типа» бивектора.

Вот пример: вы могли видеть, что векторы нормалей преобразуются иначе, чем обычные векторы, с помощью «обратного переноса» матрицы $(\mathbf{M}^{T})^{-1}$ , вместо самой матрицы. Так происходит, потому что на самом деле они на самом деле являются не векторами, а бивекторами, которые «преобразованием типов» превратили в векторы. В физике есть хак под названием «осевой вектор», который был введён для того, чтобы отличать векторы, получаемые векторным произведением, от обычных векторов. Бивектор является истинным «типом» объекта и должен восприниматься и обрабатываться соответствующим образом.

Тривекторы

Мы можем продолжать брать внешнее произведение для получения не только ориентированных 2D-площадей, но и ориентированных 3D-объёмов. Тривектор $inline$ можно получить, дважды выполнив внешнее произведение:

$\mathbf{T} = \mathbf{a} \wedge \mathbf{b} \wedge \mathbf{c}$

В трёхмерном пространстве всё на этом заканчивается. Как и в 2D, где есть только одна плоскость, заполняющая всё 2D-пространство, в 3D есть только один объём, заполняющий всё 3D-пространство.

[Но в nD мы можем продолжать создавать ещё большие внешние произведения векторов, пока не достигнем n-ного измерения. Например в 4D у нас есть четыре базисных тривектора (3-вектора) ( $\mathbf{xyz}$ , $\mathbf{xyw}$ , $\mathbf{xwz}$ , $\mathbf{yzw}$ ) и один базисный 4-вектор $\mathbf{xyzw}$ ]

В 3D тривектор имеет только один базисный компонент ( $T_{xyz}$ ), равный объёму параллелепипеда, образованного тремя векторами. Тройное внешнее произведение является улучшенной версией скалярного тройного произведения ( $(\mathbf{a} \times \mathbf{b}) \cdot \mathbf{c}$ ), потому что в нём задействован только один тип операций, оно возвращает корректный тип (объём вместо скаляра) и работает в любом количестве измерений.

$\mathbf{T} = T_{xyz} \mathbf{x} \wedge \mathbf{y} \wedge \mathbf{z}$

3. Геометрическое произведение

3.1. Умножение векторов друг на друга

Геометрическое произведение $\mathbf{a b}$ (обозначаемое без символа) — это ещё одна операция, которую можно выполнить с векторами. Геометрическое произведение определяется так, что векторы имеют обратные величины (например $\mathbf{a} \mathbf{a}^{-1}= 1$ , где 1 — это просто число 1!) и обладают удобными свойствами, например ассоциативностью ( $\mathbf{a} (\mathbf{b} \mathbf{c}) = (\mathbf{a} \mathbf{b}) \mathbf{c}$ ). Цель этого в том, чтобы иметь возможность перемножать векторы так, чтобы (как и в случае с матрицами) умножение соответствовало геометрическим операциям.

Примечание

Наличие обратных величин полезно, потому что каким бы ни был объект $\mathbf{a} \mathbf{a}^{-1}$ , он не повлияет на векторы, то есть будет вести себя так же, как и при умножении числа на 1.

Чтобы определить произведение, сначала заметим, что можно разделить произведение (или любую функцию, получающую два аргумента) на сумму части, которая не изменяется, если мы поменяем аргументы местами, и на ту часть, которая изменится, следующим образом:

$\begin{eqnarray}\mathbf{a} \mathbf{b} &=& \frac{1}{2} (\mathbf{a} \mathbf{b} + \mathbf{a} \mathbf{b} + \mathbf{b} \mathbf{a} - \mathbf{b} \mathbf{a}) \\ &=& \frac{1}{2} (\mathbf{a} \mathbf{b} + \mathbf{b} \mathbf{a}) + \frac{1}{2} (\mathbf{a} \mathbf{b} - \mathbf{b} \mathbf{a})\end{eqnarray}$

Первый член больше не зависит от порядка аргументов $\mathbf{a}$ и $\mathbf{b}$ (он называется «симметричной» частью), а второй член при перемене мест аргументов меняет знак (он называется «антисимметричной» частью).

Скалярное произведение двух векторов (также называемое внутренним произведением) симметрично и является мерой расстояния ( $\mathbf{a} \cdot \mathbf{a} = \|\mathbf{a}\|^2$ ), поэтому с геометрической точки зрения кажется полезным, чтобы мы сделали его равным симметричной части:

$\frac{1}{2} (\mathbf{a} \mathbf{b} + \mathbf{b} \mathbf{a}) = \mathbf{a} \cdot \mathbf{b}$

Аналогично, внешнее произведение двух векторов антисимметрично, поэтому полезно будет приравнять его к антисимметричной части:

$\frac{1}{2} (\mathbf{a} \mathbf{b} - \mathbf{b} \mathbf{a}) = \mathbf{a} \wedge \mathbf{b}$

Кроме того, скалярное произведение содержит косинус угла между двумя векторами ( $\mathbf{a} \cdot \mathbf{b} = \|\mathbf{a}\|\|\mathbf{b}\|cos(\alpha)$ ), в то время как внешнее произведение содержит синус угла. Вместе они полностью описывают угол между векторами, а также образуемую ими плоскость.

Примечание

Именно полнота описания делает произведение обратимым, потому что мы можем перейти от одного вектора к другому с помощью информации, содержащейся в их произведении. Если я дам вам $\mathbf{a}$ и $\mathbf{a} \mathbf{b}$ , то вы сможете получить $\mathbf{b}$ . Это невозможно сделать, зная только косинус или только синус/плоскость.

То есть геометрическое произведение равно:

$\mathbf{a} \mathbf{b} = \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \wedge \mathbf{b}$

Это странно, потому что умножение двух векторов даёт сумму двух различных вещей: скаляра и бивектора. Однако это похоже на то, как комплексное число является суммой скаляра и «мнимого» числа, поэтому вы уже могли к этому привыкнуть. Здесь часть с бивектором соответствует «мнимой» части комплексного числа. Только это не «мнимое» значение, это просто бивектор, который мы по-настоящему можем показать графически!

По сути, перемножив два вектора, мы вычисляем их полезные свойства («длину их проекций друг на друга» / «косинус угла» ( $\mathbf{a} \cdot \mathbf{b}$ ) и «плоскость, которую они вместе образуют» / «синус угла» ( $\mathbf{a} \wedge \mathbf{b}$ )), которые мы соединяем вместе знаком «плюс». Геометрическое произведение также даёт операции «групп свойств», которые к ним можно применить, и эти операции имеют геометрические интерпретации (например: поворот и отражение векторов). Это мы скоро увидим.

Можно выразить геометрическое произведение через синус и косинус: $\mathbf{a} \mathbf{b} = \|\mathbf{a}\|\|\mathbf{b}\| ( cos(\alpha) + sin(\alpha) \mathbf{B} )$ , где $\mathbf{B}$ — это бивектор обоих векторов на плоскости, составленный из двух единичных перпендикулярных векторов.

3.2. Таблица умножения

Таблица умножения позволяет сделать произведение более конкретным: давайте посмотрим, что произойдёт, если мы получим произведения базисных векторов ( $\mathbf{x}$ , $\mathbf{y}$ , $\mathbf{z}$ ).

Для любого базисного вектора, например оси $\mathbf{x}$ , результат будет равен $inline$ :

$\mathbf{x} \mathbf{x} = \mathbf{x} \cdot \mathbf{x} + \mathbf{x} \wedge \mathbf{x} = 1$

Для любой пары базисных векторов, например, осей $\mathbf{x}$ и $\mathbf{y}$ , результат будет бивектором, который они вместе образуют:

$\mathbf{x} \mathbf{y} = \mathbf{x} \cdot \mathbf{y} + \mathbf{x} \wedge \mathbf{y} = \mathbf{x} \wedge \mathbf{y}$

(то есть мы можем назвать $\mathbf{x} \wedge \mathbf{y}$ просто $\mathbf{x} \mathbf{y}$ , так как это одно и то же!)

Это даёт нам следующую таблицу:

$\mathbf{a} \mathbf{b}$		$\mathbf{b}$
$\mathbf{a} \mathbf{b}$		$\mathbf{x}$	$\mathbf{y}$	$\mathbf{z}$
$\mathbf{a}$	$\mathbf{x}$	$inline$	$\mathbf{x} \mathbf{y}$	$\mathbf{x} \mathbf{z}$
	$\mathbf{y}$	$-\mathbf{x} \mathbf{y}$	$inline$	$\mathbf{y} \mathbf{z}$
	$\mathbf{z}$	$-\mathbf{x} \mathbf{z}$	$-\mathbf{y} \mathbf{z}$	$inline$

По сути, эта таблица тривиальна, по сравнению, например, с таблицей кватернионов.

Примечание

Например, вот умножение двух векторов $inline$ и $inline$ :

$\begin{eqnarray}( 5 \mathbf{x} + 3 \mathbf{y} ) ( 2 \mathbf{x} + 1 \mathbf{z} ) &=& 5 \ 2 \ \mathbf{x} \mathbf{x} + 5 \ 1 \ \mathbf{x} \mathbf{z} + 3 \ 2 \ \mathbf{y} \mathbf{x} + 3 \ 1 \ \mathbf{y} \mathbf{z}\\ &=& 10 + 5 \ \mathbf{x} \mathbf{z} - 6 \ \mathbf{x} \mathbf{y} + 3 \ \mathbf{y} \mathbf{z} \end{eqnarray}$

3.3. Формула отражения (традиционный вид)

Отражение на вектор [в оригинале статьи каждый вектор можно перемещать]

Если у нас есть единичный вектор $\mathbf{a}$ и вектор $\mathbf{v}$ , мы можем отразить $\mathbf{v}$ через плоскость, перпендикулярную $\mathbf{a}$ .

Это делается обычным образом: мы разделяем $\mathbf{v}$ на часть, перпендикулярную к плоскости: $\mathbf{v}_\perp = (\mathbf{v} \cdot \mathbf{a}) \mathbf{a}$ , и часть, параллельную плоскости: $\mathbf{v}_\parallel = \mathbf{v} - \mathbf{v}_\perp = \mathbf{v} - (\mathbf{v} \cdot \mathbf{a})\mathbf{a}$ .

Затем, для того, чтобы отразить вектор, перевернём перпендикулярную часть, а параллельную оставим неизменной:

$\begin{eqnarray}R_{\mathbf{a}}(\mathbf{v}) &=& \mathbf{v}_\parallel - \mathbf{v}_\perp \\ &=& ( \mathbf{v} - (\mathbf{v} \cdot \mathbf{a})\mathbf{a} ) - ((\mathbf{v} \cdot \mathbf{a}) \mathbf{a}) \\ &=&\mathbf{v} - 2 (\mathbf{v} \cdot \mathbf{a}) \mathbf{a}\end{eqnarray}$

3.4. Формула отражения (вид для геометрического произведения)

На этом этапе мы можем заменить скалярное произведение $\mathbf{v} \cdot \mathbf{a}$ на его версию в виде геометрического произведения $\frac{1}{2} (\mathbf{v} \mathbf{a} + \mathbf{a} \mathbf{v})$ , и получить следующее:

$\begin{eqnarray}R_{\mathbf{a}}(\mathbf{v}) &=& \mathbf{v} - 2(\frac{1}{2}( \mathbf{v} \mathbf{a} + \mathbf{a} \mathbf{v})) \mathbf{a} \\ &= & \mathbf{v} - \mathbf{v} \mathbf{a}^2 - \mathbf{a} \mathbf{v} \mathbf{a} \\ &= & - \mathbf{a} \mathbf{v} \mathbf{a}\end{eqnarray}$

( $\mathbf{a}^2 = \mathbf{a} \cdot \mathbf{a} = 1$ , так как $\mathbf{a}$ является единичным вектором)

Это даёт нам абсолютно то же самое, но в другой записи. Использование записи в виде простого произведения вместо формулы для кодирования такой фундаментальной операции, как отражение, будет очень полезным!

Как работает многократное геометрическое произведение

Если вы не понимаете, как работает многократное взятие геометрического произведения, то просто посмотрите на базисные векторы. Есть всего три возможных случая:

$\begin{eqnarray}\mathbf{x} (\mathbf{x} \mathbf{x}) &=& \mathbf{x} 1 = \mathbf{x} \\ \mathbf{x} (\mathbf{x} \mathbf{y}) &=& \mathbf{x} (\mathbf{x} \cdot \mathbf{y} + \mathbf{x} \wedge \mathbf{y}) = \mathbf{x} (\mathbf{x} \cdot \mathbf{y}) + \mathbf{x} \mathbf{x} \mathbf{y} = \mathbf{x} (\mathbf{x} \cdot \mathbf{y} ) + \mathbf{y} \\ \mathbf{x} (\mathbf{y} \mathbf{z}) &=& \mathbf{x} (\mathbf{y} \cdot \mathbf{z}) + \mathbf{x} \mathbf{y} \mathbf{z}\end{eqnarray}$

Результаты будут следующими: вектор, вектор, вектор + тривектор. Однако последний случай может возникнуть, только когда все три вектора независимы, что никогда не истинно для $-\mathbf{ava}$

Подробности

Любопытствующие могут посмотреть, на то, что происходит на каждом этапе $- \mathbf{a} \mathbf{v} \mathbf{a}$ с точки зрения геометрического произведения.

Первый этап:

$\mathbf{v} \mathbf{a} = \mathbf{v} \cdot \mathbf{a} + \mathbf{v} \wedge \mathbf{a}$

Если, как и раньше, мы разделим $\mathbf{v}$ на часть, перпендикулярную к плоскости ( $\mathbf{v}_\perp$ ), и часть, параллельную ей ( $\mathbf{v}_\parallel$ ), то мы получим:

$\begin{eqnarray}(\mathbf{v}_\perp + \mathbf{v}_\parallel) \mathbf{a} &=& (\mathbf{v}_\perp + \mathbf{v}_\parallel) \cdot \mathbf{a} + (\mathbf{v}_\perp + \mathbf{v}_\parallel) \wedge \mathbf{a} \\ &=& \mathbf{v}_\perp \cdot \mathbf{a} + \mathbf{v}_\parallel \cdot \mathbf{a} + \mathbf{v}_\perp \wedge \mathbf{a} + \mathbf{v}_\parallel \wedge \mathbf{a}\end{eqnarray}$

$\mathbf{v}_\parallel \cdot \mathbf{a} = 0$ , потому что эти векторы перпендикулярны, а $\mathbf{v}_\perp \wedge \mathbf{a} = 0$ , потому что эти векторы параллельны.

$\mathbf{v} \mathbf{a} = \mathbf{v}_\perp \cdot \mathbf{a} + \mathbf{v}_\parallel \wedge \mathbf{a}$

Первый член — это просто длина проекции $\mathbf{v}$ на $\mathbf{a}$ , т.е. первый член — это просто длина $\mathbf{v}_\perp$ .

Давайте назовём $\hat{\mathbf{v}_\parallel}$ нормализованной версией $\mathbf{v}_\parallel$ , то есть $\mathbf{v}_\parallel = \hat{\mathbf{v}_\parallel}\|\mathbf{v}_\parallel\|$ . Тогда второй член — это просто бивектор $\mathbf{B} = \hat{\mathbf{v}_\parallel} \wedge \mathbf{a}$ , умноженный на длину $\mathbf{v}_\parallel$ .

Этот бивектор $\mathbf{B}$ составлен из двух перпендикулярных единичных векторов, то есть это очень чистое представление плоскости векторов $\mathbf{a}$ и $\mathbf{v}$ . Он не содержит информацию об их относительном угле или их длинах, только ориентацию плоскости.

То есть оба члена являются просто разложением $\mathbf{v}$ на две ортогональные проекции ( $\mathbf{v}_\parallel$ и $\mathbf{v}_\perp$ ), а также образуемой ими плоскость ( $\mathbf{B}$ ):

$\| \mathbf{v}_\perp \| + \| \mathbf{v}_\parallel \| \mathbf{B}$

Прежде чем переходить к следующему шагу, мы можем заменить внешнее произведение геометрическим, потому что $\mathbf{a}$ и $\mathbf{v}_\parallel$ перпендикулярны, а потому их внешнее и геометрическое произведение будут эквивалентными (так так часть со скалярным произведением из их геометрического произведения равна нулю).

$\mathbf{v}_\perp \cdot \mathbf{a} + \mathbf{v}_\parallel \wedge \mathbf{a} = \mathbf{v}_\perp \cdot \mathbf{a} + \mathbf{v}_\parallel \mathbf{a}$

Второй этап будет следующим:

$\mathbf{a} \mathbf{v} \mathbf{a} = \mathbf{a} (\mathbf{v}_\perp \cdot \mathbf{a}) + \mathbf{a} \mathbf{v}_\parallel \mathbf{a}$

Первый член — это просто компонент $\mathbf{v}$ вдоль $\mathbf{a}$ , т.е. компонент $\mathbf{v}$ , перпендикулярный плоскости. Другими словами, первый член — это просто $\mathbf{v}_\perp$ .

$\mathbf{a} \mathbf{v} \mathbf{a} = \mathbf{v}_\perp + \mathbf{a} \mathbf{v}_\parallel \mathbf{a}$

Так как $\mathbf{a}$ и $\mathbf{v}_\parallel$ (снова) перпендикулярны, их геометрическое произведение просто является их внешним произведением, то есть можно поменять их местами и изменить знак.

$\begin{eqnarray}\mathbf{a} \mathbf{v} \mathbf{a} &=& \mathbf{v}_\perp - \mathbf{v}_\parallel \mathbf{a} \mathbf{a} \\ &=& \mathbf{v}_\perp - \mathbf{v}_\parallel\end{eqnarray}$

И наконец, последний этап переворачивает знак:

$-\mathbf{a} \mathbf{v} \mathbf{a} = -\mathbf{v}_\perp + \mathbf{v}_\parallel$

То есть мы видим, что компонент $\mathbf{v}$ , перпендикулярный плоскости, перевёрнут, а параллельная часть остаётся такой же!

Примечание

Длина $\mathbf{a}$ не очень важна, поэтому ниже мы её игнорируем, но если $\mathbf{a}$ не является единичным вектором, то мы должны выполнить деление на его длину и формула превращается в $- \mathbf{a} \mathbf{v} \mathbf{a}^{-1}$ , что больше походит на «послойное произведение», к которому вы уже должны были привыкнуть.

3.5. Два отражения — это поворот: ситуация в 2D

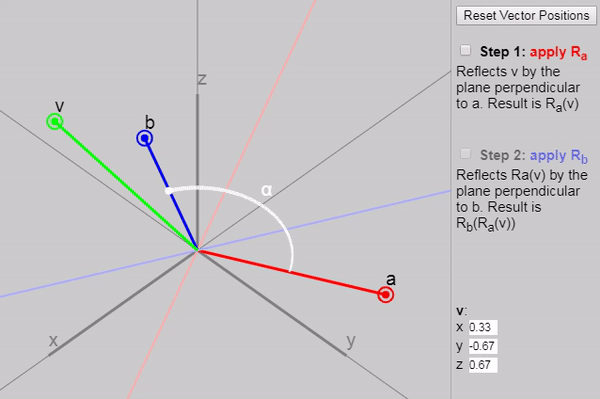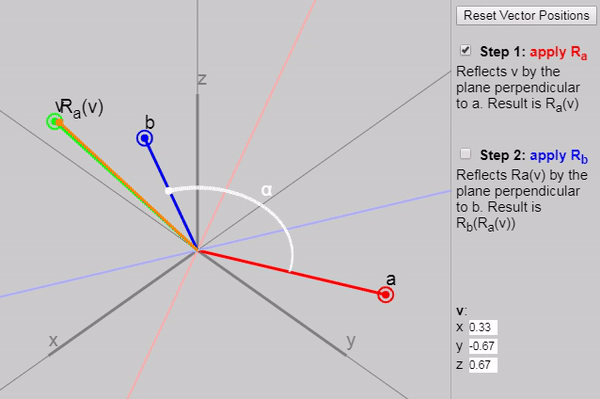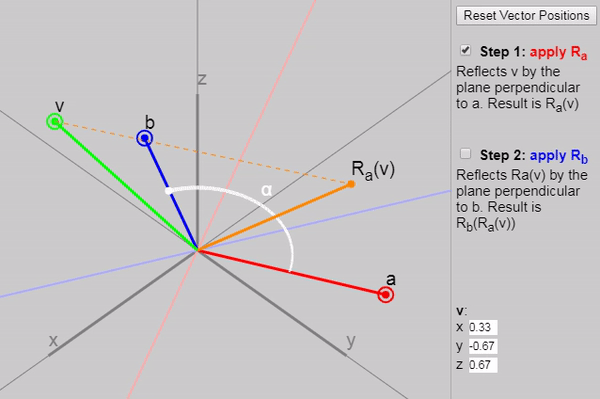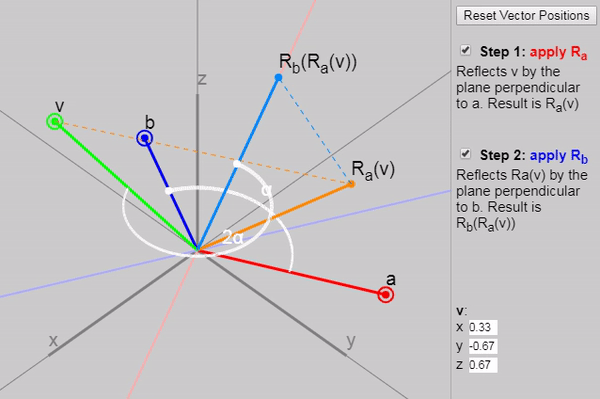
Оказывается, что если мы применим к $\mathbf{v}$ два последовательных отражения (сначала с вектором $\mathbf{a}$ , а затем с вектором $\mathbf{b}$ ), то получим поворот на удвоенный угол между векторами $\mathbf{a}$ и $\mathbf{b}$ .

Мы можем показать каждый последующий этап отражения на показанном ниже графике:

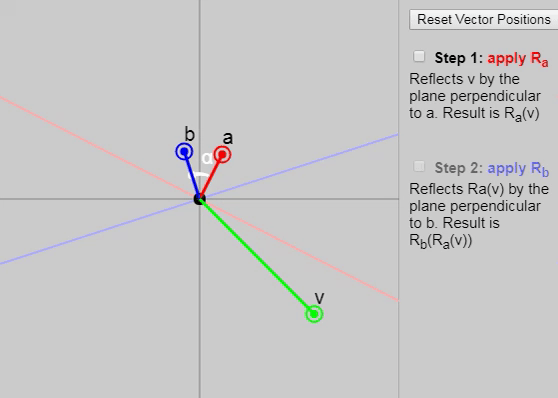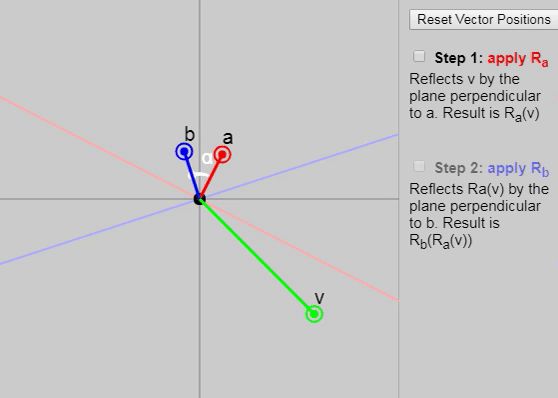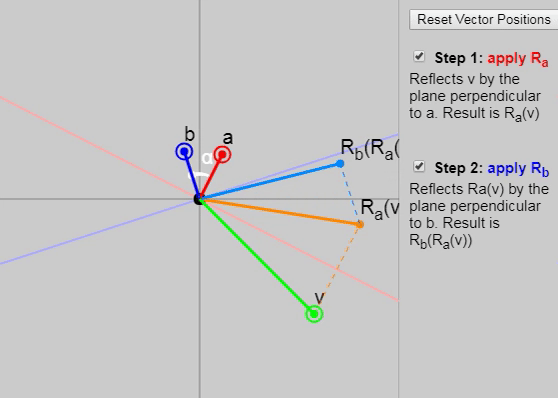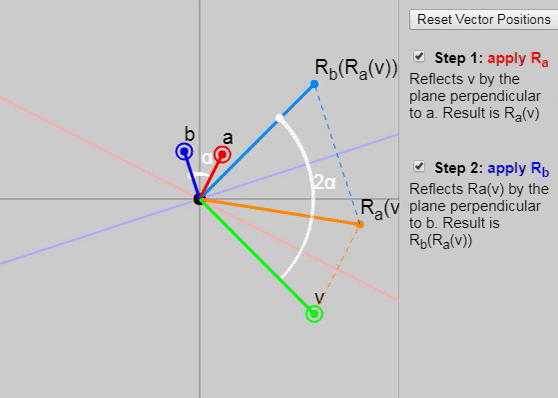
Также в оригинале статьи можно изменить векторы $\mathbf{a}$ , $\mathbf{b}$ и $\mathbf{v}$ , но исходная конфигурация векторов на графике (нажмите на кнопку «Reset Vector Positions») особенно явно демонстрирует, почему поворот в результате происходит на удвоенный угол. Ещё одна неплохая конфигурация — задание в качестве $\mathbf{a}$ и $\mathbf{b}$ осей $\mathbf{x}$ и $\mathbf{y}$ .

3.6. Два отражения — это поворот: ситуация в 3D

В случае 3D вектор $\mathbf{v}$ можно разделить на две части, одна из которых лежит на плоскости, заданной $\mathbf{a}$ и $\mathbf{b}$ , а другая лежит снаружи плоскости (перпендикулярна ей). Как показано на графике ниже, когда вектор отражается каждой из плоскостей, его внешняя часть остаётся той же. Что касается внутренней части, то мы возвращаемся в 2D, и она просто поворачивается на удвоенный угол!

3.7. Роторы

С точки зрения геометрического произведения два отражения просто соответствуют следующему:

$R_{\mathbf{b}}(R_{\mathbf{a}}(\mathbf{v})) = - \mathbf{b} (-\mathbf{a} \mathbf{v} \mathbf{a}) \mathbf{b} = \mathbf{b} \mathbf{a} \: \mathbf{v} \: \mathbf{a} \mathbf{b}$

Мы называем $\mathbf{a} \mathbf{b} = \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \wedge \mathbf{b}$ ротором, потому что умножая на $\mathbf{a} \mathbf{b}$ с обеих сторон вектора, мы выполняем поворот ( $\mathbf{b} \mathbf{a}$ — это то же самое, что и $\mathbf{a} \mathbf{b}$ , только в перевёрнутой частью-бивектором).

Применение ротора $\mathbf{a} \mathbf{b}$ к обеим сторонам вектора поворачивает этот вектор в плоскости векторов $\mathbf{a}$ и $\mathbf{b}$ на удвоенный угол между $\mathbf{a}$ и $\mathbf{b}$ .

И на этом всё!

Сравнение 3D-роторов и кватернионов

Можно заметить, что 3D-роторы во многом выглядят как кватернионы:

$a + B_{xy} \ \mathbf{x} \wedge \mathbf{y} + B_{xz} \ \mathbf{x} \wedge \mathbf{z} + B_{yz} \ \mathbf{y} \wedge \mathbf{z}$

$a + b \ \mathbf{i} + c \ \mathbf{j} + d \ \mathbf{k}$

На самом деле, код/математика практически те же самые! Главное различие в том, что $\mathbf{i}$ , $\mathbf{j}$ и $\mathbf{k}$ заменяются на $\mathbf{y} \wedge \mathbf{z}$ , $\mathbf{x} \wedge \mathbf{z}$ и $\mathbf{x} \wedge \mathbf{y}$ , но работают они в основном так же. Сравнение кода можно посмотреть здесь. Я не стал реализовывать всё, например log/exp для интерполяции, но их создать довольно просто.

Однако, как мы видели, 3D-роторы — это трёхмерная концепция, не требующая для визуализации использования «четырёхмерных двойных поворотов» или «стереографического проецирования». Попытка визуализировать кватернионы, работающие в 4D, для объяснения 3D-поворотов немного похожа на то, чтобы пытаться понять движение планет с геоцентрической точки зрения. Т.е. такой подход слишком сложен, потому что мы смотрим на него с неверной точки зрения.

Как мы увидели, моделирование поворотов как происходящих внутри плоскостей, а не вокруг векторов, сильно нам помогает. Например, квадраты базисных бивекторов дают $inline$ , точно так же как и базисные кватернионы ( $\mathbf{i}^2=\mathbf{j}^2=\mathbf{k}^2 = -1$ ):

$(\mathbf{x} \mathbf{y})^2 = (\mathbf{x} \mathbf{y}) (\mathbf{x} \mathbf{y}) = - (\mathbf{y} \mathbf{x}) (\mathbf{x} \mathbf{y}) = -\mathbf{y} (\mathbf{x} \mathbf{x}) \mathbf{y} = - \mathbf{y} \mathbf{y} = -1$

Умножение двух бивекторов друг на друга даёт третий бивектор, но по сути это тривиально, и нам не нужно запоминать, что $\mathbf{i} \mathbf{j} = \mathbf{k}$ :

$(\mathbf{x} \mathbf{y}) (\mathbf{y} \mathbf{z}) = \mathbf{x} (\mathbf{y} \mathbf{y}) \mathbf{z} = \mathbf{x} \mathbf{z}$

(Заметьте, что мы использовали $\mathbf{x} \wedge \mathbf{y} = \mathbf{x} \mathbf{y}$ )

Эти свойства являются следствием геометрического произведения, а не возникают ниоткуда!

Дополнительное чтение

(Кстати, в геометрической алгебре есть не только роторы, но и другие крутые штуки!)

Linear and Geometric Algebra by Macdonald [ссылка на Amazon]

Отличный источник, очень чёткий и понятный, потому что подразумевалось, что он заменит учебник линейной алгебры для студентов.
Geometric Algebra For Computer Science by Dorst et al. [ссылка на Amazon]

Отличный источник, потому что программирование иногда позволяет лучше разобраться в предмете.
Примечание: в этой книге авторы дают понять, что геометрическая алгебра медленее, чем кватернионы (и тому подобное...). На самом деле она должна иметь примерно такой же код (т.е. не стоит писать код для геометрической алгебры, создавая обобщённую struct, которая может содержать все возможные типы k-векторов, просто пишите при необходимости по одной struct для каждого типа k-векторов. То есть для замены кватернионов можно написать одну структуру Bivector и одну структуру Rotor, которая является Scalar + Bivector).

Tags:

Hubs:

If this publication inspired you and you want to support the author, do not hesitate to click on the button