Размытие изображения посредством фильтра Gaussian Blur широко используется в самых разных задачах. Но иногда хочется чуть большего разнообразия, чем просто один фильтр на все случаи жизни, в котором регулировке поддаётся только один параметр — его размер. В этой статье мы рассмотрим несколько других реализаций размытия.

Эффект Gaussian Blur является линейной операцией и математически представляет собой свёртку изображения с матрицей фильтра. При этом каждый пиксель в изображении замещается на сумму близлежащих, взятых с определёнными весовыми коэффициентами.
Фильтр называется Gaussian, потому что он строится из функции, известной как гауссиана, :
:
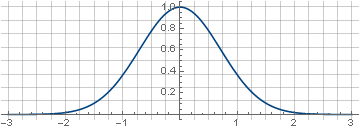
двумерный вариант которой получен её вращением относительно оси ординат, :
:
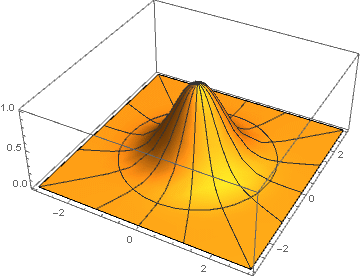
Здесь для каждой пары координат рассчитывается расстояние до центра по формуле
рассчитывается расстояние до центра по формуле  , которое передаётся как аргумент в функцию гауссианы — и, как легко увидеть,
, которое передаётся как аргумент в функцию гауссианы — и, как легко увидеть,  сокращается до
сокращается до  .
.
Матрица, построенная на отрезке![$[-3,3]$](https://habrastorage.org/getpro/habr/formulas/456/612/eb4/456612eb4809b8f3d59cc309d5f0785c.svg) и с некоторым уровнем дискретизации, будет выглядеть так:
и с некоторым уровнем дискретизации, будет выглядеть так:
Или, если рассматривать значения элементов матрицы как уровень яркости, так:

В терминах обработки сигналов это называется импульсной характеристикой, поскольку именно так будет выглядеть результат свёртки данного фильтра с единичным импульсом (в данном случае — пикселем).
Изначально гауссиана определена на бесконечном интервале. Но за счёт того, что она довольно быстро затухает, можно исключить из вычислений значения, близкие к нулю — поскольку они всё равно не отразятся на результате. В реальных приложениях также необходима нормализация по значению, чтобы после свёртки яркость изображения не изменялась; а в случае размытия изображения, в котором каждый пиксель имеет один и тот же цвет, не должно меняться и само изображение.
Для удобства часто используют нормализацию и по координатам, посредством введения дополнительного параметра (читается как «сигма») — чтобы рассматривать аргумент в диапазоне
(читается как «сигма») — чтобы рассматривать аргумент в диапазоне ![$[-1,1]$](https://habrastorage.org/getpro/habr/formulas/18f/000/34f/18f00034fa5ce903aae2db2027678177.svg) , а
, а  определяет степень сжатия гауссианы:
определяет степень сжатия гауссианы:
Нормализующий делитель здесь получен аналитически через определённый интеграл на бесконечности:
здесь получен аналитически через определённый интеграл на бесконечности:
За счёт того, что выполняется равенство , размытие по Гауссу можно реализовать последовательно сначала по строкам, а затем по столбцам — что позволяет достаточно сильно сэкономить на вычислениях. В этом случае необходимо использовать формулу с нормализацией для одномерного случая —
, размытие по Гауссу можно реализовать последовательно сначала по строкам, а затем по столбцам — что позволяет достаточно сильно сэкономить на вычислениях. В этом случае необходимо использовать формулу с нормализацией для одномерного случая —
Для произвольного фильтра нам нужно сначала определить собственную функцию затухания от одной переменной , из которой вращением получается функция от двух переменных путём замены
, из которой вращением получается функция от двух переменных путём замены  на
на  , где
, где  и
и  это координаты элемента матрицы в диапазоне
это координаты элемента матрицы в диапазоне  , и которая далее используется для заполнения элементов матрицы. Нормализацию будем считать не аналитически, а непосредственным суммированием всех элементов матрицы — это и проще, и точнее — поскольку после дискретизации функция получается «прореженной», и значение нормализации будет зависеть от уровня дискретизации.
, и которая далее используется для заполнения элементов матрицы. Нормализацию будем считать не аналитически, а непосредственным суммированием всех элементов матрицы — это и проще, и точнее — поскольку после дискретизации функция получается «прореженной», и значение нормализации будет зависеть от уровня дискретизации.
В случае, если элементы матрицы нумеруются с нуля, координата или
или  считается по формуле
считается по формуле
где — порядковый номер элемента в строке или столбце, а
— порядковый номер элемента в строке или столбце, а  — общее количество элементов.
— общее количество элементов.
Например, для матрицы 5 на 5 это будет выглядеть так:
Или, если исключить граничные значения, которые всё равно равны нулю, то координаты будут считаться по формуле
а матрица соответственно примет вид
После того, как элементы матрицы были рассчитаны по формуле, необходимо посчитать их сумму и поделить матрицу на неё. К примеру, если у нас получилась матрица
то суммой всех её элементов будет 40, и после нормализации она примет вид
и суммой всех её элементов станет 1.
Для начала возьмём самую простую функцию — линию:
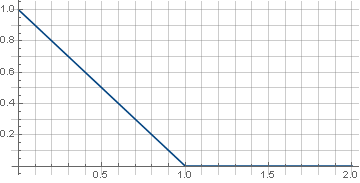
Кусочно-непрерывное определение здесь нужно, чтобы функция гарантированно уходила в ноль и при вращении не возникало артефактов на углах матрицы. Кроме того, поскольку при вращении используется корень из суммы квадратов координат, который всегда положителен, то и функцию достаточно определить только в положительной части значений. В итоге получим:
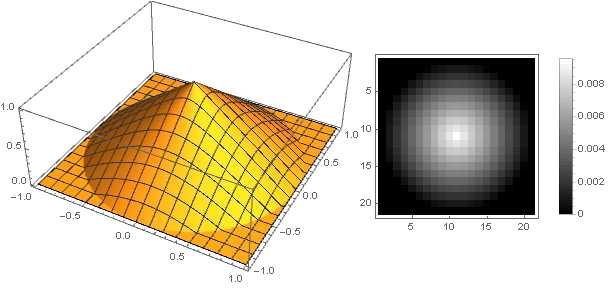
Резкий переход от наклонной линии к нулю функции может вызвать противоречие с чувством прекрасного. Для его устранения нам поможет функция
в которой определяет «жёсткость» стыковки,
определяет «жёсткость» стыковки,  . Для, например,
. Для, например,  получим
получим
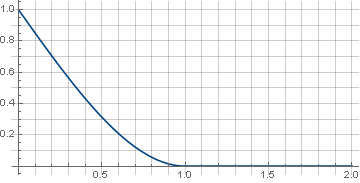
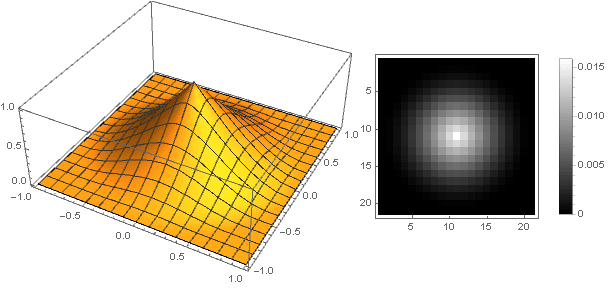
а сам фильтр будет выглядеть как
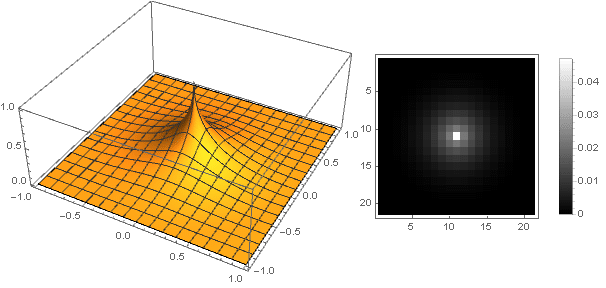
Фильтр можно сделать более «острым» и более плавно уходящим в ноль, взяв в качестве образующей другую функцию — например, гиперболу, а плавный переход к нулю обеспечив путём суммирования с параболой.
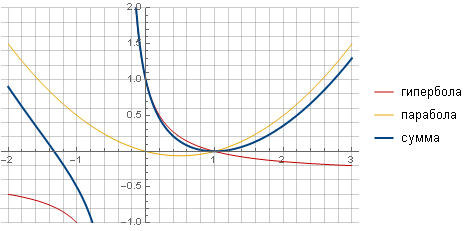
После всех вычислений и упрощений получим формулу
в которой параметр определяет характер затухания:
определяет характер затухания:
а сам фильтр будет выглядеть (для ) как
) как
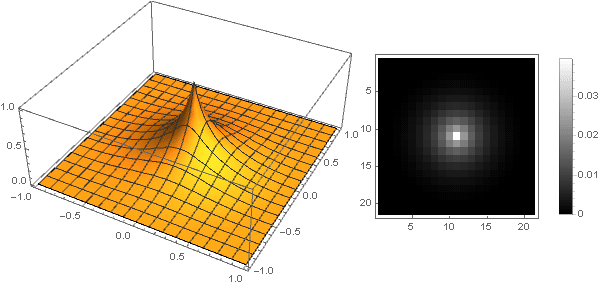
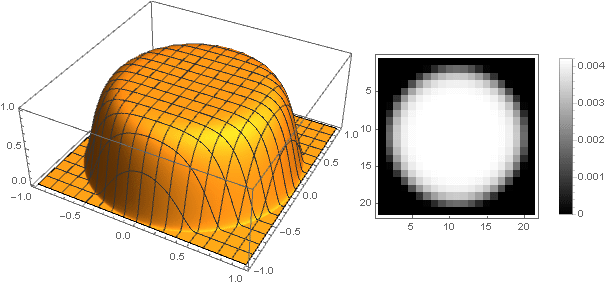
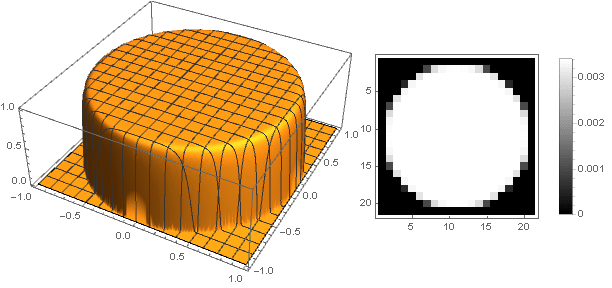
Можно пойти и другим путём — делать вершину фильтра не острой, а тупой. Наиболее простой способ реализовать это — задать функцию затухания как константу:
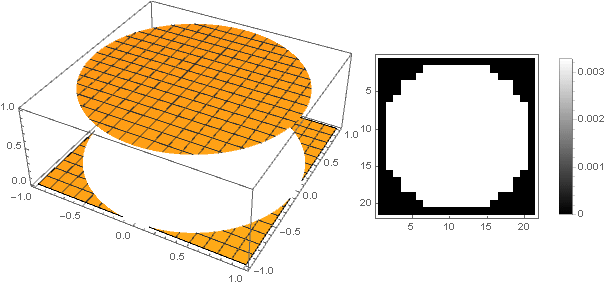
Но в таком случае мы получаем сильную пикселизацию, что контрастирует с чувством прекрасного. Сделать его более гладким на краях нам поможет парабола высших порядков, из которой посредством её смещения вдоль оси ординат и возведением в квадрат получим
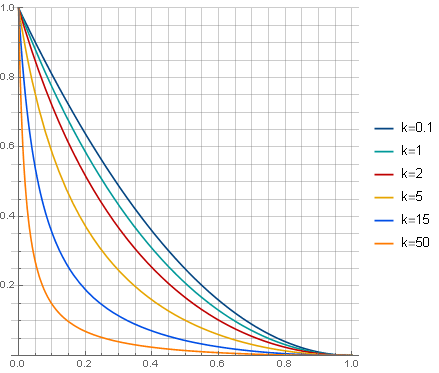
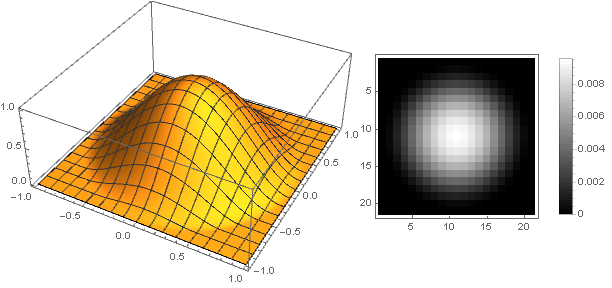
Варьируя параметр , можно получить широкий спектр вариантов фильтра:
, можно получить широкий спектр вариантов фильтра:
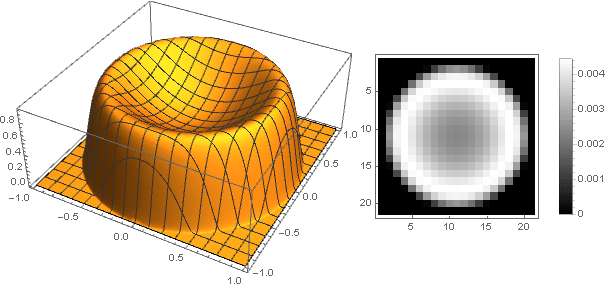
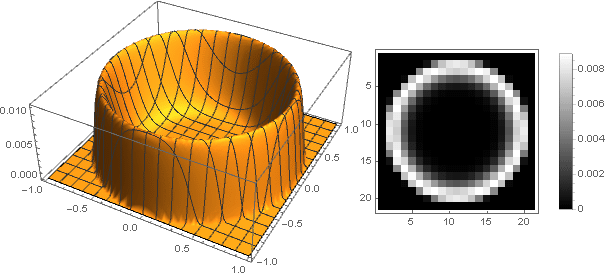
А слегка модифицировав функцию затухания, можно сделать более выраженным кольцо на краях фильтра, например так:
Здесь параметр определяет высоту центра, а
определяет высоту центра, а  — резкость перехода к краям.
— резкость перехода к краям.
Для получим
получим
а для
Можно модифицировать и непосредственно саму функцию гауссианы. Наиболее очевидный способ для этого — параметрировать показатель степени — мы сейчас рассматривать не будем, а возьмём более интересный вариант:
За счёт того, что при стремящемся к единице знаменатель
стремящемся к единице знаменатель  стремится к нулю, дробь
стремится к нулю, дробь  стремится к минус бесконечности, а сама экспонента также стремится к нулю. Таким образом, деление на
стремится к минус бесконечности, а сама экспонента также стремится к нулю. Таким образом, деление на  позволяет сжать область определения функции с
позволяет сжать область определения функции с  до
до  . При этом, при
. При этом, при  за счёт деления на ноль (
за счёт деления на ноль ( ) значение функции не определено, но имеет два предела — предел с одной стороны (изнутри) равен нулю, а с другой стороны — бесконечности:
) значение функции не определено, но имеет два предела — предел с одной стороны (изнутри) равен нулю, а с другой стороны — бесконечности:
Поскольку граничные значения в интервал не входят, то нуля в пределе только с одной стороны вполне достаточно. Интересно, что это свойство распространяется и на все производные этой функции, что обеспечивает идеальную стыковку с нулём.
Параметр определяет схожесть с гауссианой — чем он больше, тем сильнее получается схожесть — за счёт того, что всё более линейный участок
определяет схожесть с гауссианой — чем он больше, тем сильнее получается схожесть — за счёт того, что всё более линейный участок  приходиться на центр функции. Можно было бы предположить, что за счёт этого в пределе можно получить оригинальную гауссиану — но, к сожалению, нет — функции всё-таки разные.
приходиться на центр функции. Можно было бы предположить, что за счёт этого в пределе можно получить оригинальную гауссиану — но, к сожалению, нет — функции всё-таки разные.
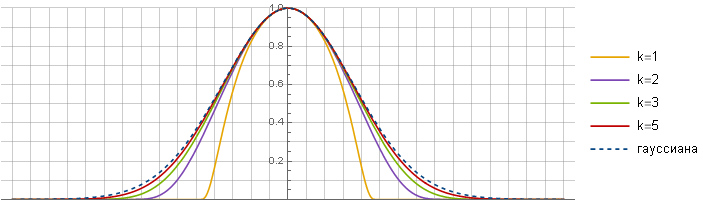
Теперь можно посмотреть, что получилось:
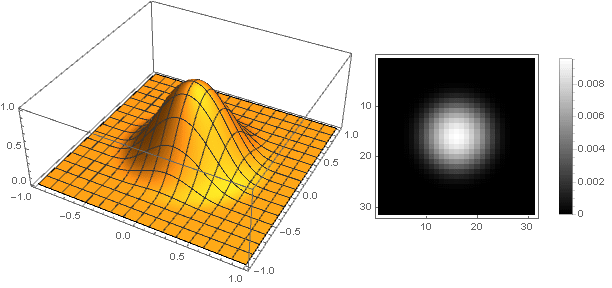
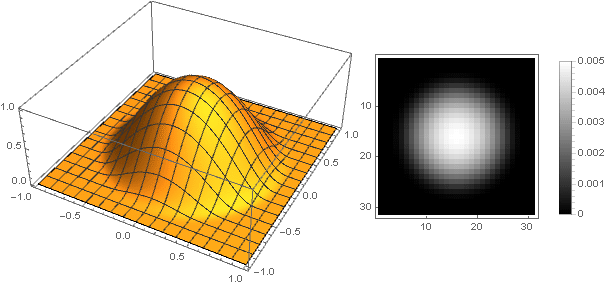
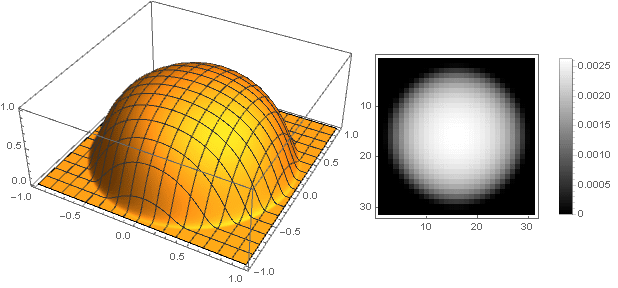
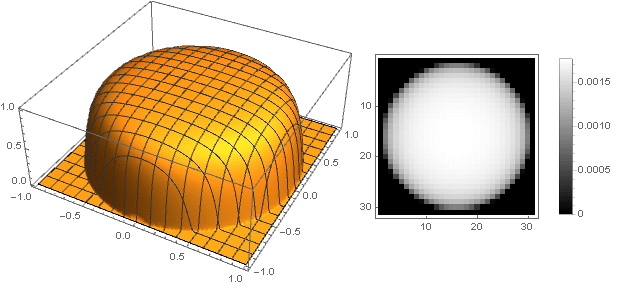
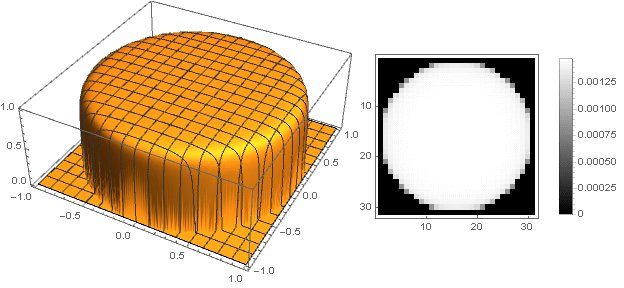
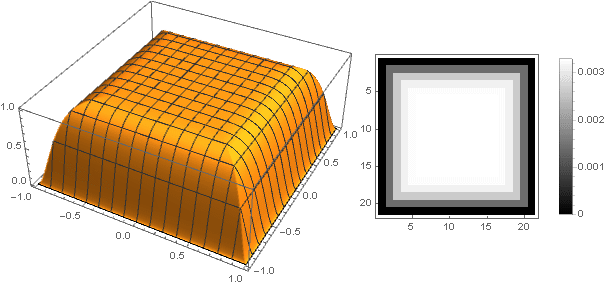
Изменив функцию перехода от двух координат к одной , можно получить и другие фигуры, а не только диск. Например:
, можно получить и другие фигуры, а не только диск. Например:
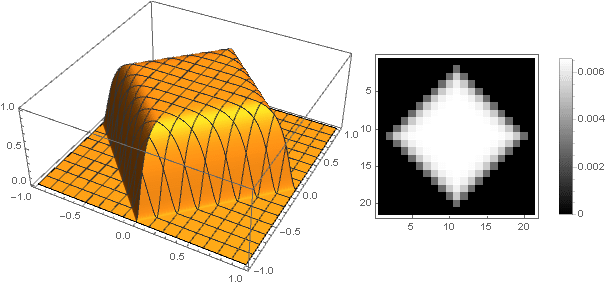
Перейдя на комплексные числа, можно конструировать и более сложные фигуры:
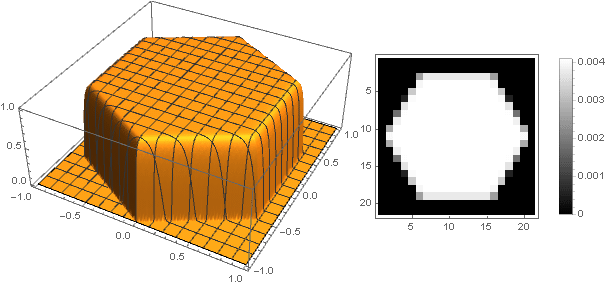
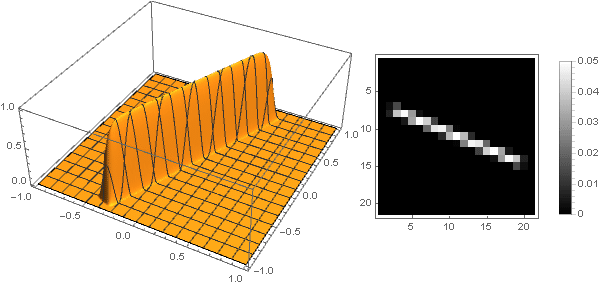
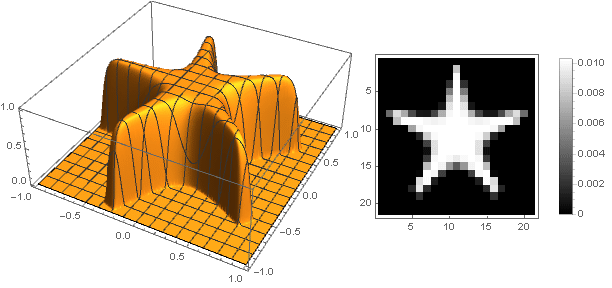
При этом нужно следить, чтобы при преобразовании координат не выходить за пределы интервала — ну или наоборот, доопределить функцию затухания для отрицательных значений аргумента.
— ну или наоборот, доопределить функцию затухания для отрицательных значений аргумента.
Статья была бы не полной без практического испытания на конкретных изображениях. Поскольку у нас не научная работа, то и изображение Лены мы брать не будем — а возьмём что-нибудь мягкое и пушистое:






Те же фильтры, но для текста:





Аналогичным образом можно строить и более сложные фильтры, в том числе и с усилением резкости или выделением контуров; а также модифицировать уже рассмотренные.
Отдельный интерес представляет и нелинейная фильтрация, когда значения коэффициентов фильтра зависят от координат или непосредственно самого фильтруемого изображения — но это уже предмет для других исследований.
Более подробно вывод функций для стыковки с константой рассматривается здесь. В качестве функции затухания также могут быть использованы оконные функции, рассмотренные здесь — нужно лишь масштабировать аргумент c (0,1) на ( ,1) или изначально считать оконные функции по формуле
,1) или изначально считать оконные функции по формуле  .
.
Исходный документ Wolfram Mathematica для этой статьи можно скачать здесь.

Введение
Эффект Gaussian Blur является линейной операцией и математически представляет собой свёртку изображения с матрицей фильтра. При этом каждый пиксель в изображении замещается на сумму близлежащих, взятых с определёнными весовыми коэффициентами.
Фильтр называется Gaussian, потому что он строится из функции, известной как гауссиана,

двумерный вариант которой получен её вращением относительно оси ординат,

Здесь для каждой пары координат
Матрица, построенная на отрезке
Или, если рассматривать значения элементов матрицы как уровень яркости, так:

В терминах обработки сигналов это называется импульсной характеристикой, поскольку именно так будет выглядеть результат свёртки данного фильтра с единичным импульсом (в данном случае — пикселем).
Изначально гауссиана определена на бесконечном интервале. Но за счёт того, что она довольно быстро затухает, можно исключить из вычислений значения, близкие к нулю — поскольку они всё равно не отразятся на результате. В реальных приложениях также необходима нормализация по значению, чтобы после свёртки яркость изображения не изменялась; а в случае размытия изображения, в котором каждый пиксель имеет один и тот же цвет, не должно меняться и само изображение.
Для удобства часто используют нормализацию и по координатам, посредством введения дополнительного параметра
Нормализующий делитель
За счёт того, что выполняется равенство
Начало
Для произвольного фильтра нам нужно сначала определить собственную функцию затухания от одной переменной
В случае, если элементы матрицы нумеруются с нуля, координата
где
Например, для матрицы 5 на 5 это будет выглядеть так:
Или, если исключить граничные значения, которые всё равно равны нулю, то координаты будут считаться по формуле
а матрица соответственно примет вид
После того, как элементы матрицы были рассчитаны по формуле, необходимо посчитать их сумму и поделить матрицу на неё. К примеру, если у нас получилась матрица
то суммой всех её элементов будет 40, и после нормализации она примет вид
и суммой всех её элементов станет 1.
Линейное затухание
Для начала возьмём самую простую функцию — линию:

Кусочно-непрерывное определение здесь нужно, чтобы функция гарантированно уходила в ноль и при вращении не возникало артефактов на углах матрицы. Кроме того, поскольку при вращении используется корень из суммы квадратов координат, который всегда положителен, то и функцию достаточно определить только в положительной части значений. В итоге получим:

Мягкое линейное затухание
Резкий переход от наклонной линии к нулю функции может вызвать противоречие с чувством прекрасного. Для его устранения нам поможет функция
в которой

а сам фильтр будет выглядеть как

Гиперболическое затухание
Фильтр можно сделать более «острым» и более плавно уходящим в ноль, взяв в качестве образующей другую функцию — например, гиперболу, а плавный переход к нулю обеспечив путём суммирования с параболой.

После всех вычислений и упрощений получим формулу
в которой параметр

а сам фильтр будет выглядеть (для

Имитация эффекта боке
Можно пойти и другим путём — делать вершину фильтра не острой, а тупой. Наиболее простой способ реализовать это — задать функцию затухания как константу:

Но в таком случае мы получаем сильную пикселизацию, что контрастирует с чувством прекрасного. Сделать его более гладким на краях нам поможет парабола высших порядков, из которой посредством её смещения вдоль оси ординат и возведением в квадрат получим
Варьируя параметр




А слегка модифицировав функцию затухания, можно сделать более выраженным кольцо на краях фильтра, например так:
Здесь параметр
Для

а для

Вариации гауссианы
Можно модифицировать и непосредственно саму функцию гауссианы. Наиболее очевидный способ для этого — параметрировать показатель степени — мы сейчас рассматривать не будем, а возьмём более интересный вариант:
За счёт того, что при
Поскольку граничные значения в интервал не входят, то нуля в пределе только с одной стороны вполне достаточно. Интересно, что это свойство распространяется и на все производные этой функции, что обеспечивает идеальную стыковку с нулём.
Параметр

Теперь можно посмотреть, что получилось:





Вариации формы
Изменив функцию перехода от двух координат к одной


Перейдя на комплексные числа, можно конструировать и более сложные фигуры:



При этом нужно следить, чтобы при преобразовании координат не выходить за пределы интервала
Несколько конкретных примеров
Статья была бы не полной без практического испытания на конкретных изображениях. Поскольку у нас не научная работа, то и изображение Лены мы брать не будем — а возьмём что-нибудь мягкое и пушистое:

Гауссиана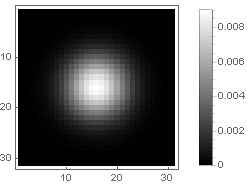


Гиперболическое затухание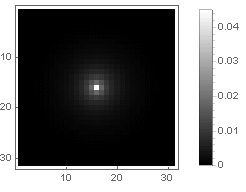


Крест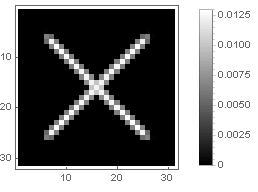


Кольцо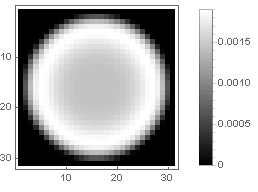


Одностороннее затухание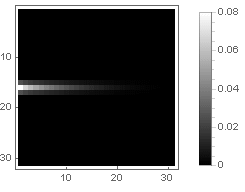


Те же фильтры, но для текста:
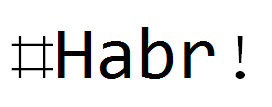





Заключение
Аналогичным образом можно строить и более сложные фильтры, в том числе и с усилением резкости или выделением контуров; а также модифицировать уже рассмотренные.
Отдельный интерес представляет и нелинейная фильтрация, когда значения коэффициентов фильтра зависят от координат или непосредственно самого фильтруемого изображения — но это уже предмет для других исследований.
Более подробно вывод функций для стыковки с константой рассматривается здесь. В качестве функции затухания также могут быть использованы оконные функции, рассмотренные здесь — нужно лишь масштабировать аргумент c (0,1) на (
Исходный документ Wolfram Mathematica для этой статьи можно скачать здесь.