О чём речь
Появление на Хабре поста о фильтре Маджвика было по-своему символическим событием. Видимо, всеобщее увлечение дронами возродило интерес к задаче оценивания ориентации тела по инерциальным измерениям. При этом традиционные методы, основанные на фильтре Калмана, перестали удовлетворять публику — то ли из-за высоких требований к вычислительным ресурсам, неприемлемых для дронов, то ли из-за сложной и неинтуитивной настройки параметров.
Пост сопровождался весьма компактной и эффективной реализацией фильтра на C. Однако судя по комментариям, физический смысл этого кода, а равно и всей статьи, для кого-то остался туманным. Что ж, признаем честно: фильтр Маджвика — самый замысловатый из группы фильтров, основанных в общем-то на очень простых и элегантных принципах. Эти принципы я и рассмотрю в своём посте. Кода здесь не будет. Мой пост — не рассказ о какой-то конкретной реализации алгоритма оценивания ориентации, а скорее приглашение к изобретению собственных вариаций на заданную тему, которых может быть очень много.
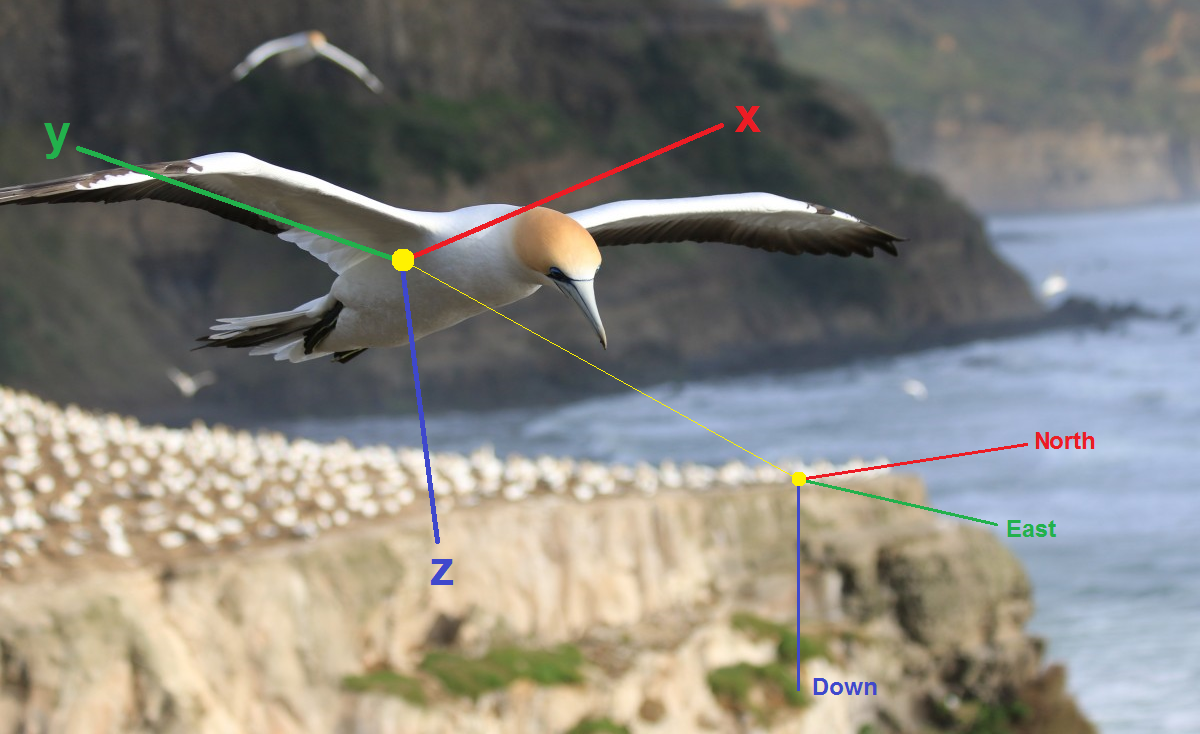
Представление ориентации
Вспомним основы. Чтобы оценить ориентацию тела в пространстве, нужно для начала выбрать какие-то параметры, которые в совокупности однозначно определяют эту ориентацию, т.е. по сути ориентацию связанной системы координат
Углы Эйлера — крен (roll,
Матрица поворота — матрица
Здесь
Матрица поворота чуть менее наглядна, чем углы Эйлера, зато в отличие от них позволяет непосредственно преобразовывать векторы и ни при каком угловом положении не лишается смысла. С вычислительной точки зрения её главный недостаток — избыточность: ради трёх степеней свободы вводятся сразу девять параметров, и все их нужно обновлять согласно кинематическому уравнению. Задачу можно слегка упростить, воспользовавшись ортогональностью матрицы.
Кватернион поворота — радикальное, но очень неинтуитивное средство против избыточности и вырождения. Это четырёхкомпонентный объект
Схемы фильтров
Самый наивный подход к вычислению ориентации — вооружиться кинематическим уравнением и обновлять в соответствии с ним любой понравившийся нам набор параметров. Например, если мы выбрали матрицу поворота, то можем написать цикл с чем-нибудь в духе
C += С * Omega * dt. Результат разочарует. Гироскопы, особенно MEMS, имеют большие и нестабильные смещения нуля — в результате даже в полном покое вычисляемая ориентация будет иметь неограниченно накапливающуюся ошибку (дрейф). Все ухищрения, придуманные Махони, Маджвиком и многими другими, не исключая и меня, были направлены на компенсацию этого дрейфа за счёт вовлечения измерений от акселерометров, магнитометров, приёмников GNSS, лагов и т.д. Так родилось целое семейство фильтров ориентации, опирающихся на простой базовый принцип.Базовый принцип. Для компенсации дрейфа ориентации нужно прибавить к измеренной гироскопами угловой скорости дополнительную управляющую угловую скорость, построенную на основе векторных измерений других датчиков. Вектор управляющей угловой скорости должен стремиться совместить направления измеренных векторов с их известными истинными направлениями.Здесь заключён совершенно иной подход, чем в построении корректирующего слагаемого фильтра Калмана. Главное отличие именно в том, что управляющая угловая скорость — не слагаемое, а множитель при оцениваемой величине (матрице или кватернионе). Отсюда вытекают важные преимущества:
- Оценивающий фильтр можно строить для самой ориентации, а не для малых отклонений ориентации от той, которую дают гироскопы. При этом оцениваемые величины будут автоматически удовлетворять всем требованиям, которые налагает задача: матрица будет ортогональной, кватернион — нормированным.
- Физический смысл управляющей угловой скорости намного яснее, чем корректирующего слагаемого в фильтре Калмана. Все манипуляции делаются с векторами и матрицами в обычном трёхмерном физическом пространстве, а не в абстрактном многомерном пространстве состояний. Это заметно упрощает доработку и настройку фильтра, а в качестве бонуса позволяет избавиться от матриц большой размерности и тяжеловесных матричных библиотек.
Теперь посмотрим, как эта идея реализуется в конкретных вариантах фильтров.
Фильтр Махони. Вся зубодробительная математика оригинальной статьи Махони написана ради обоснования несложных уравнений (32). Перепишем их в наших обозначениях. Если отвлечься от оценивания смещений нуля гироскопов, то останутся два ключевых уравнения — собственно кинематическое уравнение для матрицы поворота (с управляющей угловой скоростью в виде матрицы
Разумеется, в фильтре Махони необязательно пользоваться матрицей поворота. Есть и неканонические кватернионные варианты.
Виртуальная гироплатформа. В фильтре Махони мы прилагали управляющую угловую скорость

www.theairlinepilots.com
Задачей платформы там была материализация географической системы координат. Ориентация носителя измерялась относительно этой платформы датчиками углов на рамах подвеса. Если гироскопы имели дрейф, то вслед за ними дрейфовала и платформа, и в показаниях датчиков углов накапливались ошибки. Чтобы эти ошибки устранить, вводилась обратная связь от акселерометров, установленных на платформе. Например, отклонение платформы от горизонта вокруг северной оси воспринималось акселерометром восточной оси. Этот сигнал позволял задать управляющую угловую скорость
Теми же самыми наглядными понятиями мы можем пользоваться и в своей задаче. Выписанное кинематическое уравнение нужно тогда читать так: скорость изменения ориентации представляет собой разность двух вращательных движений — абсолютного движения носителя (первое слагаемое) и абсолютного движения виртуальной гироплатформы (второе слагаемое). Аналогию можно распространить и на закон формирования управляющей угловой скорости. Вектор
Первый намёк на полезную аналогию платформенной и бесплатформенной инерциальной навигации появляется, видимо, в древнем патенте «Боинга». Затем эта идея активно разрабатывалась Салычевым, а в последнее время — и мной тоже. Очевидные преимущества такого подхода:
- Управляющую угловую скорость можно формировать на основе понятных физических принципов.
- Естественным образом оказываются разделены горизонтальные и курсовой каналы, очень различные по своим свойствам и способам коррекции. В фильтре Махони они смешаны.
- Удобно компенсировать влияние ускорений за счёт привлечения данных GNSS, которые выдаются именно в географических, а не связанных осях.
- Легко обобщить алгоритм на случай высокоточной инерциальной навигации, где приходится учитывать форму и вращение Земли. Как это сделать в схеме Махони, я не представляю.
Фильтр Маджвика. Маджвик избрал трудный путь. Если Махони, судя по всему, интуитивно пришёл к своему решению, а потом обосновал его математически, то Маджвик с самого начала проявил себя формалистом. Он взялся решать задачу оптимизации. Рассудил он так. Зададим ориентацию кватернионом поворота. В идеальном случае расчётное направление какого-нибудь измеряемого вектора (пусть у нас это будет
Градиентный спуск в итоге приводит к следующему условию: для компенсации дрейфа ориентации нужно добавить к скорости изменения кватерниона из кинематического уравнения новое отрицательное слагаемое, пропорциональное
Влияние ускорений
До сих пор предполагалось, что истинных ускорений нет и акселерометры измеряют только ускорение свободного падения
Это легко проиллюстрировать с помощью аналогии виртуальной гироплатформы. Её система коррекции устроена так, что платформа останавливается в том угловом положении, в котором обнуляются сигналы акселерометров, якобы установленных на ней, т.е. когда измеряемый вектор
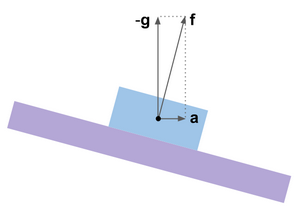
В комментариях к посту о фильтре Маджвика промелькнул вопрос о том, можно ли надеяться на то, что этот фильтр менее восприимчив к ускорениям, чем, например, фильтр Махони. Увы, все описанные здесь фильтры эксплуатируют одни и те же физические принципы и поэтому страдают от одних и тех же проблем. Обмануть физику математикой нельзя. Что же тогда делать?
Самый простой и грубый способ придумали ещё в середине прошлого века для авиационных гировертикалей: уменьшать или вовсе обнулять управляющую угловую скорость при наличии ускорений или угловой скорости курса (которая свидетельствует о входе в вираж). Тот же метод можно перенести и в нынешние бесплатформенные системы. Об ускорениях при этом нужно судить по значениям
Более точный способ основан на использовании внешних измерений скорости от приёмника GNSS. Если известна скорость
Смещения нуля датчиков
Печальной особенностью гироскопов и акселерометров потребительского класса являются большие нестабильности смещений нуля по времени и по температуре. Для их устранения недостаточно одной только заводской или лабораторной калибровки — нужно дооценивание во время работы.
Гироскопы. Разберёмся со смещениями нуля гироскопов
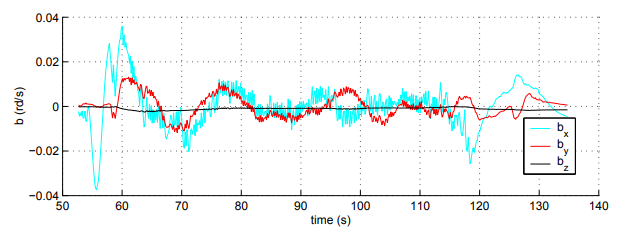
Mahony et al., 2008
Акселерометры. Оценить смещения нуля акселерометров

Вместо заключения: а что же с фильтром Калмана?
У меня нет сомнения, что описанные здесь фильтры почти всегда будут иметь преимущество перед традиционным фильтром Калмана в отношении быстродействия, компактности кода и удобства настройки — для этого они и создавались. Что касается точности оценивания, то здесь всё не столь однозначно. Мне встречались неудачно спроектированные фильтры Калмана, которые и по точности заметно проигрывали фильтру с виртуальной гироплатформой. Маджвик также доказывал выгоды своего фильтра относительно каких-то калмановских оценок. Однако для одной и той же задачи оценивания ориентации можно соорудить не менее десятка разных схем фильтра Калмана, и у каждой будет бесчисленное количество вариантов настройки. У меня нет никаких поводов думать, что фильтр Махони или Маджвика окажется точнее лучшего из возможных фильтров Калмана. И конечно, за калмановским подходом всегда останется преимущество универсальности: он не налагает никаких жёстких ограничений на конкретные динамические свойства оцениваемой системы.