Монин Илья Алексеевич, к.т.н., МГТУ им.Баумана., imoninpgd@gmail.com
Критика существующего Теоретического объяснения Подъёмной Силы на крыле самолёта
Прослушав курс лекций МФТИ Факультет аэромеханики и летательной техники (ФАЛТ) «Введение в Аэродинамику» и прочитав несколько разных ВУЗовских учеников по «Аэродинамике» [1-3], я был озадачен рядом явных противоречий в объяснениях физики процесса обтекания потоком воздуха (газа или идеальной жидкости) различных твёрдых предметов и формирования подъёмной силы на крыле.
Для полёта современного самолёта необходимая подъёмная сила в 500-600кг/м.кв. При совершении взлёта-посадки скорости современных самолётов составляют около 250км/ч. В этом случае нужная подъёмная сила на крыле обеспечивается при скорости обтекания верхней плоскости порядка 450км/ч.
Каков механизм такого разгона потока воздуха без видимого механизма разгонного воздействия на него?
Ведь контакт крыла с набегающим потоком может вести только к торможению потока, но никак не к его разгону!
Эти противоречия необходимо снять!
Физика не должна терять Физический смысл в угоду красивым и сложным математическим построениям!
Рассмотрим иное объяснение формирования подъёмной силы крыла без выявленных нарушений законов физики и здравого смысла. Для этого потребуются применение законов обычной механики.
В рассмотрении считаем, что воздух состоит из отдельных взаимно отталкивающихся (для создания давления газа) частиц с собственной массой, каждая из которых подчиняется законам механики при изменении её направления и величины скорости движения.
Рассматриваемое реальное крыло не является элементом идеальной трубки в модели Закона Бернулли, а является ограниченным твёрдым объектом в неограниченном пространстве движущегося реального газа, состоящего из вполне осязаемых по массе и размеру частиц газа. В таком случае следует рассмотреть криволинейное течение струй над криволинейной поверхностью крыла с учётом сил инерции и создаваемого давления, перпендикулярного вектору скорости и поверхности крыла.
Если рассматривать движение струй над профилем крыла, то создать разряжение над крылом может струя воздуха за счёт криволинейности своего течения.
Так для искривления прямолинейного движения тела нужно приложить силу, в перпендикулярном к вектору скорости направлении. В случае непрерывной плоской струи для её искривления нужно обеспечить разность давлений над и под ней. При этом со стороны выпуклости струи будет повышенное давлении, а с вогнутой стороны- пониженное давление.
При движении по окружности материальной точки центростремительное ускорение будет создаваться силой
F=m*V^2/R
А при таком же круговом движении тонкого слоя газа толщиной dR масса будет равна
m= q*S*dR,
где S- площадь участка слоя газа, q- плотность газа. Если привести центростремительную силу к элементарной площадке слоя газа, сила превратится в давление
P=q*V^2*dR/R
При протекании воздушной струи по поверхности крыла слой газа движется по криволинейной траектории. В каждой точке этой траектории существует свой радиус кривизны, который позволяет посчитать ИНЕРЦИОННОЕ давление газа в перпендикулярном к скорости направлении.
Таким образом, можно напрямую посчитать давление (разряжение) на крыле от слоя текущего над его поверхностью газа, при этом скорость течения газа будем всегда считать равной скорости полёта крыла Vo.
Для начала рассмотрим простейший случай крыла в виде изогнутой с радиусом R пластиной нулевой толщины. Такие тонкие изогнутые профили используют для сверхлёгких планеров в авиамоделизме.
Кстати, по привычной теории с законом Бернулли у тонкой изогнутой пластины вообще не должно быть подъёмной силы, так как длина пути под крылом и над крылом одинакова. Но подъёмная сила у тонкого крыла есть, причём весьма значительная, что однозначно показывает неправильность модели подъёмной силы с применением закона Бернулли.
Для оценочного расчёта крыла выберем привычную для малоскоростных самолётов высоту профиля 20% от ширины крыла. В данном случае за высоту профиля примем разницу высот передней и задней кромки по отношению к горизонтальному воздушному потоку (см.рис.1-3)

Рис.1. Геометрия тонкого крыла постоянной кривизны
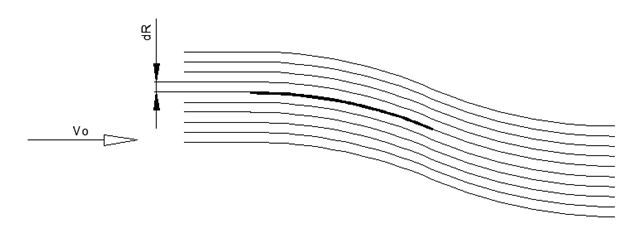
Рис.2. Предполагаемый режим обтекания тонкого радиусного крыла

Рис.3. Характер распределения давления по тонкому радиусному крылу и равнодействующие силы по направлениям
Тогда при ширине 1м и 20% высоте профиля радиус крыла составит 2,6м, при условии горизонтального расположения касательной к крылу в верхней точке профиля.
Теперь рассчитаем центростремительное давление на крыло от искривлённого по дуге слоя воздуха.
Так для скорости 70м/с (252км/ч) давление одного слоя толщиной 0,1м с радиусом кривизны 2,6м составляет 235,6Па или 24кг/м.кв., а величина скоростного напора при 70м/с равна 3063 Па.
Если учесть, что у тонкого крыла обтекание происходит с двух сторон, то эти величины нужно как минимум удвоить, а затем ещё и умножить на некоторое количество параллельных слоёв, так же искривлённых двигающимся крылом. Если предполагаем, что толщина возмущённого слоя не менее половины ширины крыла с каждой стороны крыла, то получаем суммарную удесятерённую нагрузку на крыло около 2356 Па. Эти цифры прекрасно бьются со значениями нагрузок на крыло для низкоскоростных лёгкомоторных самолётов с толстым крылом и аналогичной кривизной поверхности крыла. (см.таб.1)
Так как давление Ркр приложено к криволинейной поверхности тонкой пластины, то сила Fкр от Ркр может быть разложена на Подъёмную силы Fy и на силу Сопротивления полёту Fх.
Подъёмная сила Fy равна интегралу проекции на ось Y сил от Давления Криволинейного потока Ркр по всей площади крыла.
В случае равномерного давления на круговое крыло величина Fy будет равна произведению Ркр на площадь проекции крыла на ось Х, что равно S=B*L крыла ( в данном случае 1м.кв/м.п.).
Fy=Ркр*Bкр= 2356*1=2356 Н/м.п.
В то же время сопротивление горизонтальному движению в этом случае будет равно интегралу проекции dFкр на ось Х по всей площади крыла. В случае равномерного давления на крыло величина Fx будет равна произведению Ркр на площадь проекции крыла на ось Y, что равно высоте Н профиля крыла ( в данном случае 0,2м.кв/м.п.).
Fx=Ркр*Нкр= 2356*0,2=462 Н/м.п.
При этом получим К= Fy/ Fx= (Ркр*Bкр)/ ( Ркр*Нкр ) = Bкр/ Нкр, то есть при равномерном давлении на круговом тонком профиле качество крыла равно отношению только геометрических параметров профиля К=В/Н.
В общем виде величина К=В/Н=R*sinAк / (R*(1-cosAк))=sinAк/ (1-cosAк)
(см.график под Таб.4)
Согласно правилу векторного разложения сил из заданной картинки можно сразу получить величину качества крыла К=Fy/Fx, что в данном случае равно К=100*Ркр/20*Ркр =5.
Интересно, что если отмасштабировать данное расчётное крыло в сторону десятикратного уменьшения (по радиусу кривизны, высоте и ширине профиля), то давления на крыло при этом останутся неизменными при равных скоростях полёта (см.таб.2). Именно по этой причине тяжёлые крылатые ракеты летят на достаточно маленьких тонких крылышках. Оказывается, что их небольших по площади и тонких крыльев при достаточной кривизне действительно хватает для создания необходимой подъёмной силы!
Так как комнатный моделизм достаточно дёшев, то эти цифры достаточно просто проверяются на натурных моделях.
Таб.1. Давления искривлённых слоёв воздуха на крыло постоянного радиуса R=2,6 м в зависимости от скорости полёта.

Таб.2. Давления искривлённых слоёв воздуха на крыло постоянного радиуса R=0,26 м в зависимости от скорости полёта.

Интересно рассмотреть, как меняется Ккр крыла при постоянной его кривизне Rкр, но при изменяющемся параметре ширины профиля Вкр. (См.таб.3)
В самой первой строчке таблицы аэродинамическое качество крыла достигает фантастического значения К=182, но при этом нагрузка на крыло составляет всего 67Па (7кгс/м.кв), что пригодно только для авиамоделей планеров комнатной размерности.
Необходимая подъёмная сила на крыле возникает только при достаточно малых К крыла, что видно по последним строчкам таблицы.
Жёлтым выделены столбец изменяемого параметра и строчка исходного профиля с Ккр=5.
Таб.3. Изменение параметров крыла постоянного радиуса R=2,6м при различных углах профиля (ширина профиля) на постоянной скорости полёта.
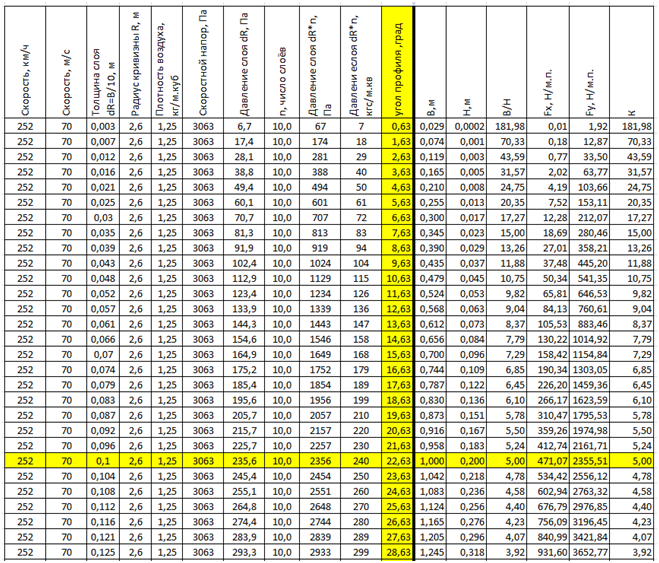
Также можно рассчитать изменение подъёмной силы Fy и качества крыла Ккр для крыла с постоянной хордой, но разной кривизной крыла при постоянной скорости. Жёлтым выделены столбцы: Изменяемый аргумент Rкр- радиус кривизны и постоянная ширина профиля Вкр. Так же выделена строчка исходного профиля с Ккр=5.
Таб.4. Изменение параметров крыла переменного радиуса кривизны при постоянной ширине профиля В=1м на постоянной скорости полёта. Ниже график качество крыла К (синим, значения по оси Y) и график Fу ( красным, в безразмерном масштабе) в зависимости от угла Ак кривизны профиля крыла по оси Х.
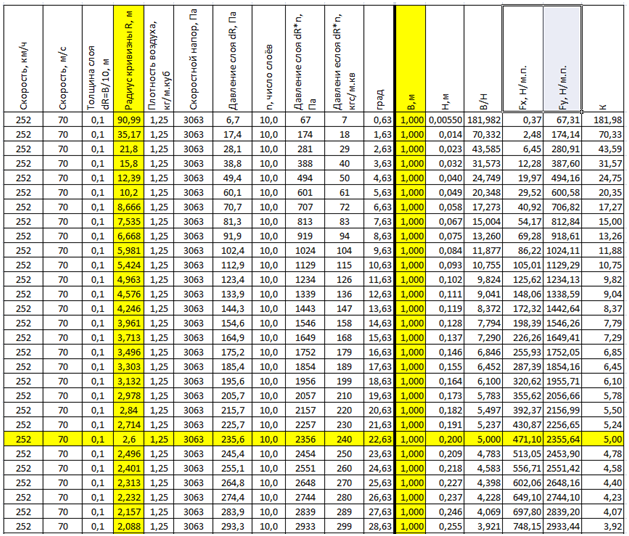
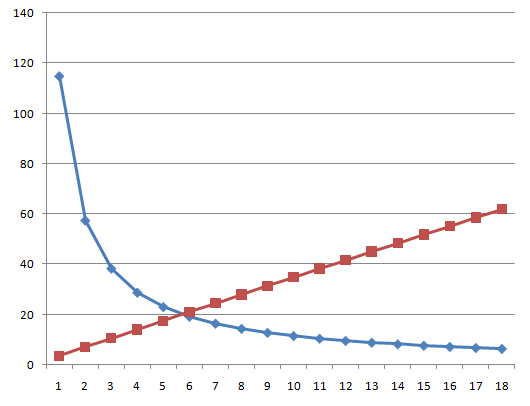
Граф. Зависимость качества крыла (синим) и подёмной силы (красным) от угла профиля Ак по оси X. По оси Y отложены величины качества крыла в безразмерных единицах. Размерность подёмной силы по оси Y условно не показана.
В описанной модели для получения разряжения над крылом не требуется дополнительный разгон воздуха над крылом. Заметное разряжение над крылом обеспечивается в условиях значительного искривления обтекающего крыло потока воздуха под действием статических сил давления воздуха всего окружающего пространства. Угол наклона хорды исходной изогнутой пластины составляет 11,3 градуса (половина угла сегмента дуги в 22,6град), что хорошо согласуется с посадочными режимами работы крыла современных авиалайнеров при посадке с выпущенной механизацией крыла (предкрылки +закрылки). В посадочном режиме крыло с выпущенной механизацией намного больше напоминает рассмотренный случай изогнутой тонкой пластинки, чем классическое крыло с прямой нижней плоскостью (см.рис 4).

Рис.4. Крыло несимметричного профиля с плоской нижней обтекаемой поверхностью: а) выпрямленное положение для скоростного полёта; б) крыло с максимальной кривизной при полностью выпущенной механизацией.
Сильно изогнутое тонкое крыло широко применяется в качестве лопастей вентиляторов. Низкие линейные скорости при малых величинах давления позволяют использовать в вентиляторах в качестве лопастей тонкие стальные или пластиковые пластины крайне малой толщины, так как их прочности хватает для выдерживания имеющихся нагрузок.
У тяжёлых самолётов использование тонких крыльев технически невозможно по причине их недостаточной прочности. Большая толщина крыла позволяет разместить внутри крыла достаточно высокие несущие балки достаточной прочности и жёсткости на изгиб и кручение, при этом сохранив приемлемый для самолёта вес. Именно по этой причине вся аэродинамика изучает крылья со вполне осязаемой толщиной. По этой причине переходим от рассмотрения аэродинамики тонкой изогнутой пластины к профилю крыла с реальной толщиной и плоскостями различной кривизны.
В завершении рассмотрения модели обтекания тонкого крыла необходимо привести ещё одно доказательство работоспособности предложенной модели объяснения «Подъёмной силы крыла». Как известно из механики, Сила- это изменение импульса в единицу времени, то есть
F=d (m*V)/dT
В озвученной модели обтекания тонкого криволинейного крыла мы можем подсчитать подъёмную силу Fy как изменение импульса набегающего потока воздуха по вертикали, который считается как
Fy2= (dR*10*q*Vo)*Vo*sinАкр,
Где Vo-скорость крыла, dR –толщина элементарного искривляемого слоя потока воздуха в расчётной модели, 10- число искривляемых одновременно слоёв, Акр- угол схода потока с крыла к направлению исходной скорости Vo.
Проведя расчёт получим, что оба расчёта дают одинаковый результат.
Или в аналитическом виде:
Fy1=Ркр*Bкр,
Ркр= (dR*10*q*Vo)* Vo/R,
Bкр=R* sinАкр
Подставив развёртки Ркр и Bкр в выражение для Fy1 и сократив одноимённые R в числителе и знаменателе, получим:
Fy= Ркр*Bкр= (dR*10*q*Vo)*Vo*sinАкр
А значит всегда верно равенство Fy =Fy1= Fy2
То есть «Инерционно-криволинейный» метод расчёта «Подъёмной Силы» крыла даёт формулу идентичную с методом «Реактивно-Импульсной Силы» для крыла одинаковой геометрии.
Это значит, что самолёты летают не благодаря какой-то «магической» силе из «магических вихрей», а благодаря старому и понятному «Импульсу Силы» или «Реактивной тяге» при отбрасывании массы воздуха вниз.
На малых скоростях полёта при взлёте-посадке (М= 0,2 или 250км/ч) скоростной напор не превышает 3кПа (3% от Атмосферного давления на уровне моря в 100кПа), то есть он столь мал по отношению к базовому атмосферному давлению, что геометрическое сжатие потока становится визуально не обнаружимо при рисовании струйного течения у крыла.
Для создания подъёмной силы над крылом необходимо создать искривление потока так, чтобы крыло находилось в зоне вогнутости потока воздуха. Обеспечить такое искривление струи над крылом помогает кривизна верхней плоскости крыла, находящейся в аэродинамической тени носового обтекателя крыла.
При этом нижняя плоскость крыла обтекается либо по прямой, не создавая разряжения, или по вогнутой поверхности, отбрасывая поток воздуха вниз, что создаёт уже положительный прирост давления на крыле снизу и суммируется с подъёмной силой от разряжения над крылом.
Главным отличием толстого крыла от тонкой пластины в нашем случае будет появление лобового обтекателя, раздвигающего встречный поток воздуха до того, как он достигнет изогнутых плоскостей, создающих подъёмную силу.
Перед летящим толстым крылом возникает зона торможения, где скорость движения воздуха становится равной нулю (относительно крыла), а избыточное давление в этой зоне равно скоростному напору Рvo.
Нарисовать линии тока без учёта сжатия воздуха не получится, иначе придется либо принять версию об ускорении воздуха над поверхностью крыла, либо зона влияния с искривлением потока устремится к бесконечности в несжимаемой среде, что является неправдоподобным.
Кстати, оба эффекта (Ускорение потока и Бесконечная зона влияния в несжимаемых жидкостях) проявляются на практике в аэродинамических трубах с дымовыми линиями тока и при движении подводных лодок на малых глубинах.
Так в аэродинамических трубах (АДТ) обтекание тестируемых макетов происходит с заметным ускорением потока (уменьшение толщин дымовых линий ) в зазоре стенка АДТ-макет. Вот только толкование этого явления совершенно неверно относят к ускорению потока для формирования подъёмной силы. В действительности ускорение потока в зазоре «стенка АДТ-макет» является просто следствием заужения проходного сечения в проточном тракте АДТ при сохранении постоянного расхода воздуха в самой АДТ за счёт мощных вентиляторов с жёсткой вентиляторной характеристикой.
При движении подводных лодок на малых глубинах над подводной лодкой образуется Визуально Заметный водяной горб. Величина этого горба равна объёму воды перед корпусом подлодки, который надо как-то переместить из зоны перед подлодкой в зону кормы при движении с заданной скоростью. Горб на поверхности образуется и при движении подлодки на больших глубинах, но из-за большей площади растекания горба его высота становится необнаружимой при простом визуальном наблюдении. Причиной возникновения горба воды на поверхности объясняется невозможностью переместить несжимаемую жидкость в сторону дна, а в сторону поверхности тонкий слой воды под атмосферным давлением воздуха становится Легко Сдвигаемым, с понятной упругой характеристикой пружины Атмосферного давления и Сил Тяготения. Кстати, даже при движении подводных лодок на больших глубинах водяной горб (и саму подлодку как следствие) могут обнаружить при наблюдении со спутников с помощью высокочувствительной аппаратуры, способной замерять геометрию поверхности морей с большой точностью и вычленить горб воды от подлодки из шума волн на поверхности с помощью ЭВМ.
Таким образом, принимаем газ сжимаемым, а зону влияния от огибания крыла ставим в зависимость от величины сжатия струи от давления Рvo.
Давление в зоне торможения у обтекателя удерживается искривлёнными струями воздуха, огибающими обтекатель. Связь давления с искривлением слоёв воздуха такая же, как и в случае с тонким изогнутым крылом dP=q*Vo^2*dR/Rсл.
Величина зоны влияния, где заметно искривление потока, также связано с величиной Вкр и Нкр. Повышение давления перед обтекателем будет скомпенсировано понижением давления в спутной струе позади крыла, то есть крыло формирует линейный Диполь по давлению, который на большом удалении практически перестаёт влиять на окружающее воздушное пространство на малых (дозвуковых) скоростях полёта.
Если принять форму носового обтекателя круглой, то половина высоты профиля будет равна Нкр/2=Rлоб.
Считаем, что зона торможения с давлением Рvo целиком создаётся кривизной слоя в границах ширины профиля Вкр, тогда можем оценить радиус кривизны струи толщиной Нкр/2= Rлоб.
Необходимо выполнить условие Pr= Рvo.
Следовательно
qVo^2*Rлоб/R= qVo^2/2
После сокращения одинаковых членов плотности и скорости соответственно в левой и правой части уравнения получаем
R= 2* Rлоб
Таким образом, получается, что предельные радиусы кривизны набегающего потока ограничены исключительно кривизной обтекателя (локальной высотой профиля), и при этом не зависят от скорости.
При повороте набегающей струи в обход профиля неизбежно возникает ситуация, в которой граничная с нулевой линей потока струя касается обтекателя. В этой точке касания скорость потока направляется от крыла, а кривая потока достигает точки перегиба. То есть в этой точке происходит отрыв слоя от крыла с изменением направления выпуклости кривизны струи (см.рис.5).
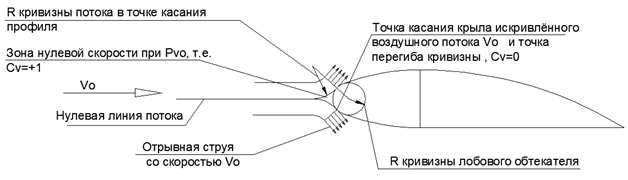
Рис.5. Взаимодействие набегающего потока Vo с лобовым обтекателем крыла.
На больших скоростях полёта величина скоростного напора Pvo столь велика, что струя отрывается от носового обтекателя и, описав длинную дугу над плоскостью крыла, возвращается обратно к поверхности крыла.
В месте возврата оторванной струи на плоскость крыла возникает Удар, а струя скачком меняет направление на касательное к плоскости крыла. При этом под дугой летящей струи от точки отрыва до точки возврата возникает замкнутая полость низкого давления. (см.рис.6).
В традиционной «Бернуллиевской Аэродинамике» описанное образование развитого отрывного пузыря с сильным разряжением и ударный возврат отрывной струи объясняют так: « …На высоких предзвуковых и трансзвуковых скоростях возникает ускорение потока воздуха над крылом до сверхзвуковых значений, в результате чего давление над крылом сильно снижается, а потом возникает скачёк давления (удар перехода на сверхзвук), с переходом после него на дозвуковое течение…». Такое объяснение выглядит как явная натяжка реальных экспериментальных данных на несостоятельную теорию.
Так как обтекатель делит набегающий поток на две части по нулевой линии, то отрыв потока возникает на обеих плоскостях крыла. Но из-за различных направлений плоскостей по отношению к потоку (на поток или в аэродинамической тени) отрывные пузыри разряжения над и под крылом имеют разный размер, и так же изменяется сила удара возвратной струи, пропорционально размеру отрывного пузыря.
На основе такого распределения эпюр давления на переднем обтекателе крыла и полученых качеств Ккр тонких радиусных пластин-крыльев в зависимости от относительной толщины профиля Вкр./Нкр. легко можно понять причины и закономерности такого явления, как «Обтекаемость» различных геометрических форм (см.Эпюру Сх на рис.6).
Так же было бы крайне интересно рассмотреть эпюры давления при Обтекании струйными течениями стандартных осесимметричных тел и получить их равёртки Сх и Су по сечениям, а не только один суммарный коэффициент Сх для фигуры в целом.

Рис.6. Обтекание струями воздуха толстого крыла с обозначенными характерными элементами движения. Эпюра давлений на крыло и диаграммы коэффициента давления Су по хорде крыла и Сх по высоте крыла. Площадь закрашенных зон соответствуют суммарным силам по направлениям Y и Х соответственно.
При низких числах М основная подъёмная сила формируется в зоне носового обтекателя в отрывных пузырях. При малых числах М возвратная струя в зоне отрыва идёт по касательной к толстому профилю крыла и не вызывает Удара в точке возврата. Но при приближении к М=1 отрывные пузыри раздуваются на столько сильно, что становится невозможно добиться нужной толщины профиля для безотрывного течения струи, и тогда возникает выраженный Отрыв потока с образованием Отрывного Пузыря, визуально наблюдаемого по колебаниям шелковинок, наклеенных на плоскость крыла. Раздувание отрывных пузырей по высоте становится препятствием для набора скорости, и потому их развитие начинают уменьшать за счёт заострения носовой кромки (понижение радиуса лобового обтекателя).
При трансзвуковых скоростях полёта задняя граница отрывного пузыря достигает задней кромки крыла, после чего происходит соединение объёмов верхнего отрывного пузыря с зоной высокого давления нижней плоскости крыла. В объединившихся объёмах верхнего и нижнего отрывных пузырей давление выравнивается, а подъёмная сила крыла Fy резко падает.
При сверхзвуковом полёте крыло привычной каплевидной формы становится уже совсем неприменимым, а вместо этого появляется крыло с развитым острым «клювом», на котором теперь и создаётся основная часть подъёмной силы, при этом минимизируется возможность возникновения отрывного пузыря.
Для обеспечения посадочных режимов полёта на низких числах Маха в «тонкоклювое» крыло осуществляют установку передней и задней отклоняемой механизации (см.рис.7). Подобного типа тонкие крылья с острыми передними кромками и отклоняемой передней и задней механизацией ставят на боевые истребители 4-5 поколений (см.фото.1-2). При отклонения механизации вниз «тонкоклювое» крыло становится близко к характеристикам обтекания тонкой изогнутой пластины, что позволяет осуществлять взлёт и посадку на малых скоростях и с коротким пробегом по ВПП. В перспективе возможен переход на поворот плоскости крыла целиком при выполнении манёвров на малых скоростях, как это уже сделано с полностью поворотным хвостовым оперением истребителей. Полностью поворотная плоскость крыла позволит избегать сильного задирания фюзеляжа против потока воздуха и сохранения сонаправленности вектора тяги двигателей к скорости полёта на больших углах атаки.
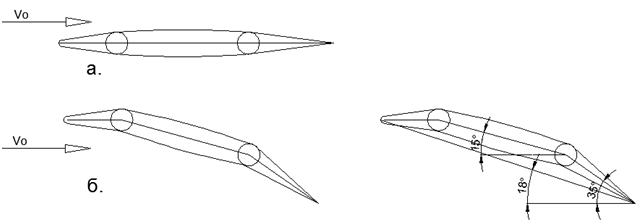
Рис.7. Профиль тонкого крыла Н/В=0,1 (10%) с острым отклоняемым «Клювом» и широким отклоняемым закрылком: а) выпрямленное положение для сверхзвукового полёта; б) отклонение механизации вниз для полётов на малых скоростях и в посадочном режиме с большими углами атаки.

Фото.1. Су- 35 на большом угле атаки с отклонёнными предкрылками и закрылками в посадочном режиме (выпущены шасси).

Фото.2. МиГ-29 с отклонёнными предкрылками и закрылками во взлёт-посадочном режиме на большом угле атаки и низкой скорости (выпущены шасси).

Фото.3. МиГ-29 на взлёте с полным отклонением вниз передней и задней механизации крыла.
На фото (см.фото.3) хорошо видна форма «остроклювого» предкрылка в сечении: плоская нижняя грань и радиусная верхняя грань. Сама передняя кромка отнюдь не острая, а имеет весьма конкретный малый радиус, тем самым улучшая аэродинамику дозвукового полёта. Управление наклоном предкрылка к набегающему потоку позволяет оптимизировать режим образования отрывного пузыря на низких скоростях, создав условия для его безотрывного схлопывания. Так же, учитывая фигуры высшего пилотажа с возможностью длительного полёта вверх ногами, отклоняемый вверх предкрылок позволяет сделать обратный прогиб плоского тонкого крыла для вполне эффективного полёта в перевёрнутом положении, хотя и с худшей аэродинамикой, чем в нормальном положении. На более поздних самолётах Су-35 и Су-57 передняя кромка острее и более симметрично клиновидная, так как рассчитана на более длительный сверхзвуковой полёт.
В сети можно найти массу объяснительного материала по любому вопросу, в том числе и к Вихреобразованию на крыле самолёта, например такой:

В тоже время в том же интернете легко найти Фотографии вихревых следов от самолётов в облачных слоях, которые демонстрируют гораздо больший масштаб явления, чем это нам пытаются показать в теории.

Фото.4. Вихревой след в слое тумана за летящим на высоте самолётом. Кольца видимого туманного вихря отстоят от самолёта на сотни метров, а визуальная близость – это оптическая иллюзия, созданная длиннофокусным телеобъективом при съёмке самолёта с дистанции в несколько километров.

Фото.5. Вихревой след в слое тумана за летящим на высоте самолётом. Виден вертикальный поток воздуха и заходящие с боков волны воздуха, закручиваемые в спираль при соприкосновении с вертикальным нисходящим потоком.

Фото.6. Вихревой след в слое тумана над ВПП за приземляющимся самолётом.
Эти огромные спутные вихри за самолётами формируются вовсе не за счёт концевых вихрей на крыле. Концевые вихри существуют, конечно, но их роль не так велика и с ним активно и успешно борются конструкторы самолётов.
Крупномасштабные вихри с фотографий формируются уже далеко за самолётом, когда волна воздуха, отброшенная самолётом вниз, замещается с двух боковых сторон перетоком воздуха из-под нисходящего слоя в разреженное пространство сверху (см.фото.4-5).
Шедевральное видео про визуализацию вихря за самолётом. В переувлажнённом воздухе конденсат выпадает во всём объёме воздуха за самолётом, тем самым визуализируя масштабное аэродинамическое явление в процессе реального полёта, лучше чем дымами в АДТ.
dzen.ru/video/watch/63badf7a0f646d4b9a595f89
Как альтернатива в сухом воздухе нет следа даже от работы двигателя (см.видео) dzen.ru/video/watch/64c68a149ab9276d36a64f22
Это объяснение образования спутного вихря перекликается с уже рассмотренным вопросом «зоны влияния крыла на окружающее пространство». При этом роль земной поверхности заключается в Границе распространения вниз отброшенного крылом вниз потока воздуха. То есть полёт самолёта и создание «подъёмной силы крыла» возможен и при отсутствии твёрдых подстилающих поверхностей, но при этом отброшенный вниз поток воздуха будет бесконечно долго двигаться вниз, по мере удаления теряя скорость и кинетическую энергию, но сохраняя неизменным вертикальный импульс. Кинетическая энергия первоначальной отброшенной массы воздуха будет теряться на вовлечение в движение боковых потоков воздуха, симметричная разнонаправленность которых не будет изменять исходный суммарный импульс, созданный крылом самолёта. Наглядной иллюстрацией роли Земли-Ограничителя является Фото.6. Там прямолинейный ток тумана над садящимся аэробусом (см.фото.6) опускается до земли по прямой и только потом далеко за самолётом начинается сдвиг в стороны вдоль земли-ограничителя, а слои тумана с боков и сверху уже надвигаются в середину спутного слоя, закручиваясь в двойную самокомпенсирующуюся спираль о нисходящий поток.
В свете изложенной роли Земли при формировании «Подъёмной силы крыла» имеет смысл дополнительно рассмотреть «Экранный Эффект», который без наличия твёрдой земной поверхности не может возникнуть. Таким образом, физика Полёта крыла в Бескрайнем воздушном пространстве и на «Экранном Эффекте» вблизи Земли имеет весьма различную природу.
Влияние близко расположенной поверхности земли на подъёмную силу крыла называют «экранным эффектом». При этом эффекте резко повышается подъёмная сила крыла при полёте вблизи твёрдой поверхности (земля, вода) на высоте сопоставимой с величиной хорды крыла. Основываясь на этом эффекте даже появился целый класс низко летающих аппаратов- «Экранопланов».
В чём же суть явления? Разобраться с этим вопросом можно только предположив, что воздух является Сжимаемым газом.
Тогда при полёте крыла над поверхностью земли образуется воздушный зазор ограниченного размера между двумя твёрдыми поверхностями. При полёте крыла с небольшим положительным углом атаки встречный поток воздуха под крылом испытывает постепенное сжатие от передней кромки крыла к задней кромке (см.рис.8).
Максимальное давление сжатия об экран потока под крылом зависит только от скоростного напора относительно летящего крыла, и это давление в сжатом слое не может превысить давление скоростного напора воздуха:
Ро=Vо^2*Q/2,
где Ро- скоростной напор воздуха при скорости крыла Vо, Vо-скорость полёта крыла, Q-плотность воздуха.
Зная максимальное приращение давления под крылом, рассчитаем геометрические параметры в зазоре «воздушной подушки».
Так при скорости 40 м/с (144км/ч) скоростной напор Ро= 1кПа или 1% от 1атм. (100кПа).
То есть на скорости 40 м/с максимальное давление под крылом достигается при сжатии на 1% по высоте Х зазора от передней кромки крыла к задней. На глаз такое поджатие практически необнаружимо, а слой под крылом визуально кажется плоским (см.рис.8.а).
При этом угол атаки составит А=(Ро/Ратм)*Х/В радиан (при малых углах sinA=A),
где В- хорда крыла, Х- величина воздушного зазора до земли под крылом на уровне задней кромки крыла, Ро- скоростной напор воздуха при скорости крыла Vо, Ратм- атмосферное давление (на уровне моря Ратм= 100кПа).
Получается, что максимально эффективный угол атаки для получения экранного эффекта зависит от высоты полёта крыла над поверхностью, конструктивной ширины крыла и заданной скорости полёта, а угол атаки оказывается лишь производной этих величин.
Вывод: Можно почти бесконечно наращивать ширину крыла, сводя угол атаки почти к нулю, тем самым достигая минимального сопротивления Сх при практически обнуленной индуктивной составляющей сопротивления.
«Экранный эффект» на низких скоростях полёта обеспечивает очень высокое качество крыла, так как создаёт максимальную удельную подъёмную силу на крыле, равную скоростному напору Ро при крайне малых углах атаки на практически плоском и очень тонком крыле. Качество крыла на малых числах Маха при полёте на экране может достигать величины К=25-30.
Вклад разрежения над верхней выпуклой поверхностью крыла при таком полёте на «экране» с плоским крылом достаточно мал в сравнении с давлением под крылом.
При повышении скорости полёта скоростной напор растёт квадратично, а для получение максимального экранного эффекта приходится задирать угол атаки пропорционально росту скоростного напора Ро.
То есть наращивание скорости Vо с целью увеличения Ро влечёт Квадратичное к росту скорости увеличение Угла атаки, что в свою очередь резко снижает качество крыла. И начиная с некоторой скорости Vо-max величина экранного эффект с большим углом атаки сравнивается с подъёмной силой обычного авиалайнера в посадочном режиме с выдвинутой механизацией крыла.
Для любого крыла с хордой В для увеличения высоты полёта Х необходимо задирать угол атаки, после чего Экраноплан поднимется на некоторую новую высоту Х2, где опять установится баланс степени поджатия струи за счёт нового угла атаки на новой высоте. При этом с увеличением высоты полёт экраноплана начинает линейно возрастать сопротивление полёту и соответственная ему потребная сила тяги тоже возрастает без изменения скорости полёта. То есть топливная экономичность полёта экраноплана может разительно изменяться от подъёма по высоте всего на несколько метров. Например, максимальная дальность полёта экранолёта «Иволга» на высоте 0,8 м составляет 1150 км, а на высоте 0,3 метра с той же нагрузкой — уже 1480 км.
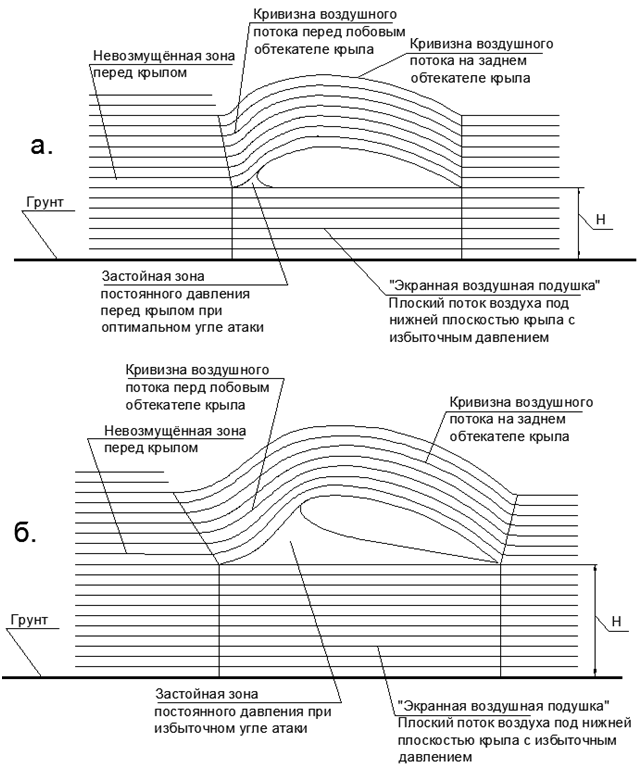
Рис.8. Конфигурация воздушных потоков на «Экранном эффекте»: а.) Оптимальный угол атаки без застойной зоны под крылом, б.) Избыточный угол атаки, формирующий большой пузырь застойного воздуха повышенного давления между крылом и поджатым слоем воздуха «Экранной воздушной подушки».
Вывод: Дополнительное задирание угла атаки крыла без увеличения скорости полёта на экране не даёт приращения подъёмной силы, а лишь увеличивает сопротивление полёту Сх (см.рис.8.б)
Считая угол хорды крыла авиалайнера в посадочном режиме около 15 градусов можем оценить величину сжатия струи под крылом до давления Ро и соответствующей ему скорости Vо, считая при этом величину хорды В равной высоте полёта крыла Х.
15 градусов соответствует sin15= 0,262
При угле атаки 15 градусов должен быть скоростной напор Ро=0,26атм= 26кПа, но такие давления реализуются на очень высоких скоростях (740км/ч) и намного превосходят необходимые для полёта расчётные нагрузки на крыло. То есть такой большой Посадочный угол атаки для создания экранного эффекта над ВПП является избыточным на посадочных скоростях 250-300 км/ч.
Качество крыла при угле атаки 15 градусов упадёт до величины всего К=3,7.
Посадочная скорость авиалайнера всего около 250км/ч (70м/с), при этом скоростной напор составит Ро=3кПа или всего 3% от Ратм, тогда как нормальна расчётная нагрузка на крыле в полёте составляет 5кПа (500кг/м.кв=5% от Ратм). То есть при посадке экранный эффект у авиалайнера начинает заметно ощущаться пилотом на высоте соизмеримой с шириной крыла В, сопоставимой с высотой стоек шасси. Выравнивание самолёта и снижение угла атаки для скорости 250км/ч позволяет самолёту пробить «экранную воздушную подушку», так как её несущая способность оказывается ниже, чем потребное давление под крылом для полёта.
За счёт «Экранного эффекта» возникает «Несажаемость» у самолёта в горизонтальном полёте без выпуска механизации крыла при угле атаки 5% (или 3 град.) при скоростном напоре Ро=5кПа, что соответствует Vо=324км/ч или 90м/с.
Угол атаки 5% (или 3 град.) создаёт качество крыла экраноплана равное К=20.
Высокий К=30 соответствует углу атаки в 3% (2 град), при этом подпор под крылом составит всего 3% * Ратм = 3кПа (300кг/м.кв), что соответствует скоростному напору при Vо=70м/с (250 км/ч).
Таким образом, экономически эффективные режимы полёта в режиме «экраноплана» в сравнении с обычным высотным «самолётом» лежат в зоне малых скоростей. При падении качества крыла экраноплана ниже К=20 выгоднее использовать для транспортировки обычный высотный самолёты. То есть экономически выгодные области эксплуатации Экранопланов соответсвуют скоростям ниже 300км/ч.
Отдельного рассмотрения заслуживает вопрос маневрирования Экраноплана в полёте. Так как подъёмная сила крыла на «экране» формируется иначе, чем при высотном полёте, то и маневрировать «по- самолётному» экраноплан не может.
Экраноплан не может закладывать виражи с креном на крыло, так как он немедленно получит потерю подъёмной силы на задранном крыле и касание воды опущенным крылом. Для экраноплана поворот возможен только «блинчиком», то есть совершенно без крена, а только за счёт создания боковых сил от вертикального оперения.
Само вертикальное оперение Экраноплана тоже должно отличаться от самолётного оперения. Вертикальное оперение Экраноплана должно состоять как минимум из двух килей, способых работать как синхронно, так и вразнобой, что зависит от типа выполняемого манёвра. Вертикальное оперение при этом не только осуществляет разворот Экраноплана вокруг его вертикальной оси, но и создаёт горизонтальную силу поперёк направления скорости полёта.
Горизонтальное оперение на заднем киле выполняет регулирование по углу атаки.
Широкое и короткое крыло необходимо оснащать развитыми концевыми шайбами-скегами, удерживающими спресованый под крылом поток от растекания в стороны. Дополнительно эти шайбы-скеги выполняют роль посадочных понтонов для приводнения.
Также нужно дополнительное горизонтальное оперение на концах основного крыла для компенсации опрокидывающего момента от действия вертикального оперения.
Практически по такой Схеме был построен экраноплан Бартини ВВА-14 (см.рис.9) и многочисленные версии перспективных макетов экранопланов-самолётов, где роль переднего вертикального оперения выполняют скеги-концевые шайбы (см.рис.10).

а.

б.

в.
Рис.9 Экраноплан Бартини ВВА-14. а.Чертёж. б. Модель в 3-Д. в. Фото действующего образца на воде.

Рис.10. Макет перспективного большого экраноплана.
Типы манёвров экраноплана за счёт вертикального оперения:
Все эти режимы практически мало реализуемы в ручном режиме, так как малая высота полёта просто не оставляет времени на реакцию в темпе человеческого восприятия. Для управления Экранопланом нужна автоматизация управлением, подобная автоматической стабилизации сверхнеустойчивых истребителей 4-5 поколения.
Все выше сказанные предположения строятся на открыто опубликованных экспериментальных данных (полученные на АДТ эпюры давления на крыле и другие данные).
В экспериментальную Аэродинамику за последний век вбуханы огромные деньги на строительство АДТ различных типов и размеров, так же получен огромный объём фактического материала в экспериментах с макетами различных летательных аппаратов и отдельных элементов крыла.
Вызывает удивление тот факт, что в процессе обучения студентов опираются не на материалы реальных Экспериментов, а на сомнительные теории 100 летней давности. И это при том, что сами экспериментальные данные явно противоречат, этим замшелым Теориям.
Даже в таком обобщённом вводном курсе, как «Введение в Аэродинамику» для ФАЛТ Физтеха, качественные объяснительные модели базового понятия «Подъёмной Силы Крыла» не даются, а вытеснены заумным наукообразным жонглированием математическими формулами (которые к тому же не позволяют ничего рассчитать).
В науке наметился тренд к расколу между теорией и практическим инженерным приложением в разработках конкретных изделий. Явные противоречия в Теоретических моделях не афишируются, а наоборот всячески замалчиваются, дабы не поколебать авторитет замшелых и уже покойных старцев из академии наук и не прервать победного шествия их искренних заблуждений по страницам вполне современных учебников и монографий.
P.S. После публикации первой части этой статьи в обсуждение под статьёй пришло сообщение, что приблизительно те же идеи были высказаны ещё в 2003 году профессором Кембриджа, преподающим там курс «Аэродинамики». В сообщении была дана ссылка на видео с лекцией профессора на эту тему, а также ссылка на статью, где на последней странице описан ровно тот же способ формирования давления изгибаемой струёй воздуха, что и я изложил в данной статье.
Меня несказанно обрадовало, что теперь мне не требуется отбиваться от всех нападок самому, а можно просто сослаться на Кембриджского профессора и его статью в британском научном журнале от 2003г.
Вот сообщение с сылками:
"
JoeHopkins7
24 февраля 2019 в 22:35
–1
Просматривая различные видео про аэродинамику, я наткнулcя на интересную лекцию по аэродинамике профессора Кембриджа.
Ещё в 2003г Кембриджский профессор излагает студентам на лекции ровно те же мысли, что и автор обсуждаемой здесь статьи.
У меня даже закрались подозрения, что автор просто плагиатор.
Но так как он на английских учёных в статье не ссылался, и для своей защиты этих видео в обсуждении не приводил, то можно поверить в его честном самостоятельном открытии чужого открытия.))
Вот ссылка на лекцию
www.youtube.com/attribution_link?a=nfUWqs-6T7M&u=%2Fwatch%3Fv%3DH2RRiF24L4A%26feature%3Dshare&fbclid=IwAR2NOfdqNs0HK9WbCp-OYwy0Y4LYK0ajPPcqV_TCHVqDPOl7yqFpoMfsQ68
Там же есть ссылка на статью, где ещё в 2003году профессор кембриджского университета в английском научном журнале пишет ровно тоже самое, что и автор статью на Хабре
www3.eng.cam.ac.uk/outreach/Project-resources/Wind-turbine/howwingswork.pdf
.."
Монин Илья Алексеевич, к.т.н., imoninpgd@gmail.com
Для понимания порядка развития «авиации» как отрасли промышленности и «аэродинамики» как науки нужно вспомнить, что сначала появились первые самолёты, построенные энтузиастами-инженерами по наитию (см.рис.11), а уж только потом начали появляться теоретики, создавшие за тем дисциплину «Аэродинамика» на основании результатов творения инженеров-конструкторов.
На картинке самолёт созданный автомобилистом Анри Фарманом переделкой из купленного мелкосерийного самолёта Вуазена. При этом исходный самолёт братьев Вуазенов начал производится только в 1907г. На момент покупки Фарманом самолёты Вуазена могли приразгоне только слегка подпрыгивать и пролетать при этом несколько десятков метров. Фарман, после ряда переделок исходного самолёта, добился возможности пролететь более 1000м, при этом ещё развернуться и, сделав круг, совершить посадку. Произошёл рекордный полёт Фармана 13 января 1908г. А уже в 1909 году фирма братьев Фарман открывает своё производство самолётов собственной конструкции и лётную школу по обучению искусству полёта на них (см.рис.12). Скорость полёта самолётов Фармана тогда составляла около 60км/ч, которая была показана в рекордном полёте на дистанцию 180км, преодолённую за 3 часа полёта.

Рис.11. Макет самолёта Вуазена, переделанного под рекордный полёт Фарманом в 1907-1908гг.


Рис.12. Макет самолёта «Фарман IV-1910.» в музее, и фото подлинного образца на аэродроме.
Понятно, что первые ранние самолёты были маломощные, лёгкие и низкоскоростные.
Именно этим параметрам соответствуют первые выпукло-вогнутые тонкие профили, больше похожие на простейший изогнутый лист фанеры, а не на сложный профиль с глубоким теоретическим просчётом.
Для справок привожу иллюстрацию трансформации профилей крыла от самых ранних начала 20-го века, до вполне развитой авиапромышленности середины 40-х годов. (см.рис.13)

Рис.13. Тенденции изменения профиля крыла самолётов первой половины 20-го века.
После первых лёгких экспериментальных самолётов последовал Быстрый рост размеров и массы самолётов для перевозки всё большей полезной нагрузки. Тонкие крылья уже никак не могли выдержать такого размаха и веса, что потребовало внутрь крыла устанавливать высокие прочные балки, а само крыло сделать плоско-выпуклым или даже двояко выпуклым, чтобы скрыть несущую балку за обтекаемой подшивкой крыла.
Уже в 20-х годах все профили крыла приняли вполне современный вид.
К 1940-м годам авиационная индустрия настолько развилась, что начала производить целые армады самолётов, способных с воздуха разносить в труху целые города. Но при столь взрывном развитии производственных мощностей теоретическая база оставалась крайне слабой.
К 30-м годам интенсивность развития авиации уже не позволяла строить новые самолёты по «наитию», а потребовало строительство мощной экспериментальной базы по продувке частей самолётов, масштабных макетов и самолётов целиком на земле в огромных аэродинамических трубах (АДТ).
Так в ЦАГИ в 1939 году была запущена крупнейшая на тот момент (вторая в мире сейчас) аэродинамическая труба Т-101, позволявшая на земле исследовать самолёты целиком на актуальных в то время скоростях полёта.
Скорость потока 5–52 м/с
Число Re на 1 м до 3.6∙106
Полное давление атмосферное
Скоростной напор до 1.7 кПа
Температура торможения окружающей среды
Диапазон углов атаки (α) ±20°
Диапазон углов скольжения (β) ±180°
Размеры рабочей части:
Сечение сопла (эллипс) 24x14 м
Длина рабочей части 24 м
Размеры объектов испытаний:
Размах крыла: до 18 м
Длина фюзеляжа: до 30 м
Площадь крыла: до 35 м2
С тех пор самолёты стали много крупнее, а скорости полёта много быстрее, так что уже ни один современный самолёт не влезает в АДТ Т-101 целиком, а в более современных и более скоростных АДТ продувают только масштабные уменьшенные макеты или элементы конструкции по отдельности.
Правда, в теории с начала прошлого века изменилось мало, так что уже в конце двадцатого века авиаконструкторы начали заново изобретать то, что уже прошли конструкторы начала-середины 20-го век, но так и не объяснили теоретики. Для примера приведу вид профиля крыла пилотажного самолёта, считавшимся лучшим ещё в 1980-х годах (см.рис.14).

Рис.14. Один из профилей крыла самолёта из каталога «Авиационные профили».
Такой же возвратный ход мысли наблюдается и среди крупных образцов лётной техники, это выразилось в создании монстров-экранопланов в 1960-80-х (рис.15), мало отличимых от гигантских самолётов конца 1930-х (рис.16).
При этом сам экранный эффект был обнаружен ещё в начале 30-х в моменты посадки крупных многомоторных самолётов с большой хордой крыла.
Так же экранный эффект ярко проявился при посадке рекордного дальнего самолёта АНТ-25, когда при испытательном полёте в 1933 году самолёт просто не мог приземлиться, а при лёгком касании колёсами земли самолёт подпрыгивал и снова взлетал. Чтобы убрать этот эффект и обеспечить спокойную посадку пришлось даже устанавливать специальные выдвижные тормозные щитки, резко ухудшающие лётные качества крыла во время посадки.
Хорда крыла в наиболее широкой корневой части у АНТ-25 превышала высоту стоек шасси, таким образом, создавались идеальные условия для формирования экранного эффекта под широким низколетящим крылом. При это во время посадки с пустыми баками при массе самолёта 4000кг и площади крыла 88м.кв, средняя нагрузка на крыле в полёте создавалась менее 50кг/м.кв, что соответствует скоростному напору 500Па создаваемому при скорости 104км/ч (29 м/с) для полёта на экране. Стоит заметить, что самолёты того времени летали крайне медленно (по современным меркам), так рекордный АНТ-25 имел крейсерскую скорость около 165км/ч (макс.246км/ч на высоте), при дальности полёта 10-12тыс.км и длительности 75-80 часов подряд.
А.
Б.
В.
Рис.15. Экраноплан «Каспийский Монстр»: а.) В полёте. Б.) Неподвижно на воде анфас. в.) Неподвижно в лобовой проекции.
А.
Б.

Рис.16. Самолёт-гигант АНТ-20 «Максим Горький», 1939г. а) Схематичный разрез. Б) Фото на аэродроме и при посадке.
Часто встречаются случаи. Когда необходимо построить линии тока воздуха вокруг тел, форму которых трудно назвать обтекаемой.
Понятно, что воздух не станет послушно обтекать все углы и выемки тела, а пойдёт мягкими извивами, проносясь над ямами и заполняя их вихрями оторванных потоков застойных зон.
Если учесть наличие застойных зон как дополнительных твёрдых объёмов самого профиля, то геометрия Обтекания известных нам аэродинамических элементов примет совершенно иной вид.
Интересно, что такой метод нахождения эквивалентного условного прототипа крыла используется и в существующей прикладной Аэродинамике. Во всяком случае метод построения «Фиктивного полубесконечного тела» вокруг твёрдого крыла описывается в учебнике[3] на целых трёх страницах(стр.435-437), при этом в качестве границ фиктивного крыла выбирают границу толстого заторможенного пограничного слоя, то есть прибавляя к крылу те самые наши застойные зоны в «отрывных пузырях» или турбулентне зоны при полном срыве потока над крылом. При этом давление на твёрдое крыло от скоростного потока воздуха считается равным давлению этого потока на «фиктивное тело». Получается, что давление передаётся от скоростной струи на твёрдое крыло через достаточно толстый слой малоподвижного воздуха пограничного заторможенного слоя (застойной зоны) без каких- либо искажений.
Рассмотрим детально процесс мягкого обтекания скоростными струями разной интенсивности профилей крыла и выделим различные «застойные зоны».
Случай полного прилипания потока к крылу на малых углах атаки особой новизны не прибавляет (см.рис.17), но появляется маленькая застойная зона на лобовом обтекателе, напоминающая маленький острый клюв на круглой голове птицы.
Элемент кажется небольшим, но он крайне важен для понимания явления «обтекания» в целом.
Рассмотрим привычный профиль крыла в горизонтальном полёте с выраженными отрывными струями сначала с нулевым углом атаки(см.рис.18), а затем это же крыло уже под большим углом атаки(см.рис.20).

Рис.17. Профиль крыла с обтеканием без отрывов на плоскостях крыла, но с маленькой зоной полного торможения потока на носовой части крыла.

Рис.18. Профиль крыла с отрывов потоков на плоскостях крыла при нулевом угле атаки и его «Фиктивное тело».
Глядя на сильное увеличение «Фиктивного тела» в сравнении с исходным расталкивающим лобовым обтекателем становится понятно как получается удивитльно низкое лобовое сопротивление у длинных веретёнообразных тел, на-пример, у фюзеляжей самолётов.
Обтекаемость таких форм достигает величины Сх=0,06, тогда как для шара такого же сечения Сх=0,4..0,5, а для плоской пластины Сх=1.
Оказывается в разряжении под отрывными струями в лобовой проекции сопротивление не создаётся совсем. Остаётся только приземлить отрывную струю на паралельную к вектору скорости прямую поверхность, чтобы при ударе не возникла продольная к скорости составляющая. С такой задачей прекрасно справляется длинный цилиндрический фюзеляж с вытянутым яйцевидным лобовым обтекателем. Получается, что лобовое сопротивление огромного фузеляжа равно сопротивлению шара на оконечности суживающейся носовой части (см.рис.19.)
Соотношение диаметра шара в носовом обтекателе к диаметру фюзеляжа зависит от скорости полёта, и чем выше скорость полёта, тем зауженней становится носовое скругление, расталкивающее воздушный поток. Возрастающая энергия встречного потока при постоянной величине лобового сечения требует разбрасывать всё меньшее количество воздуха в стороны от фюзеляжа при сохранении постоянного сечения «фиктивного тела» за обтекателем. На сверхзвуке радиус кривизны носового обтекателя вырождается в остриё, но это уже совсем другая история.
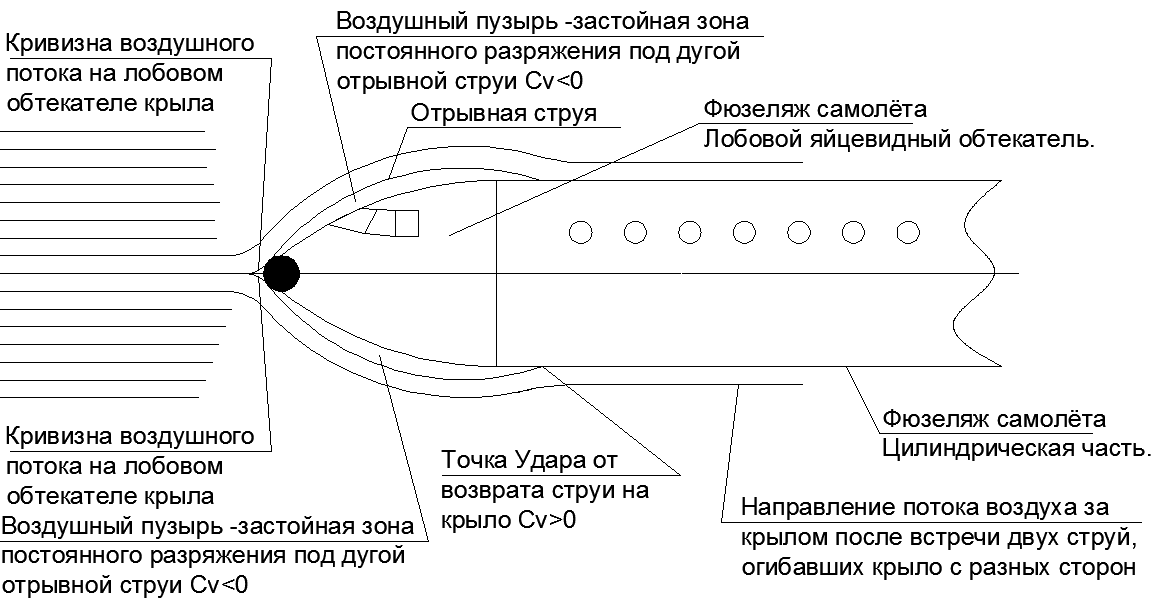
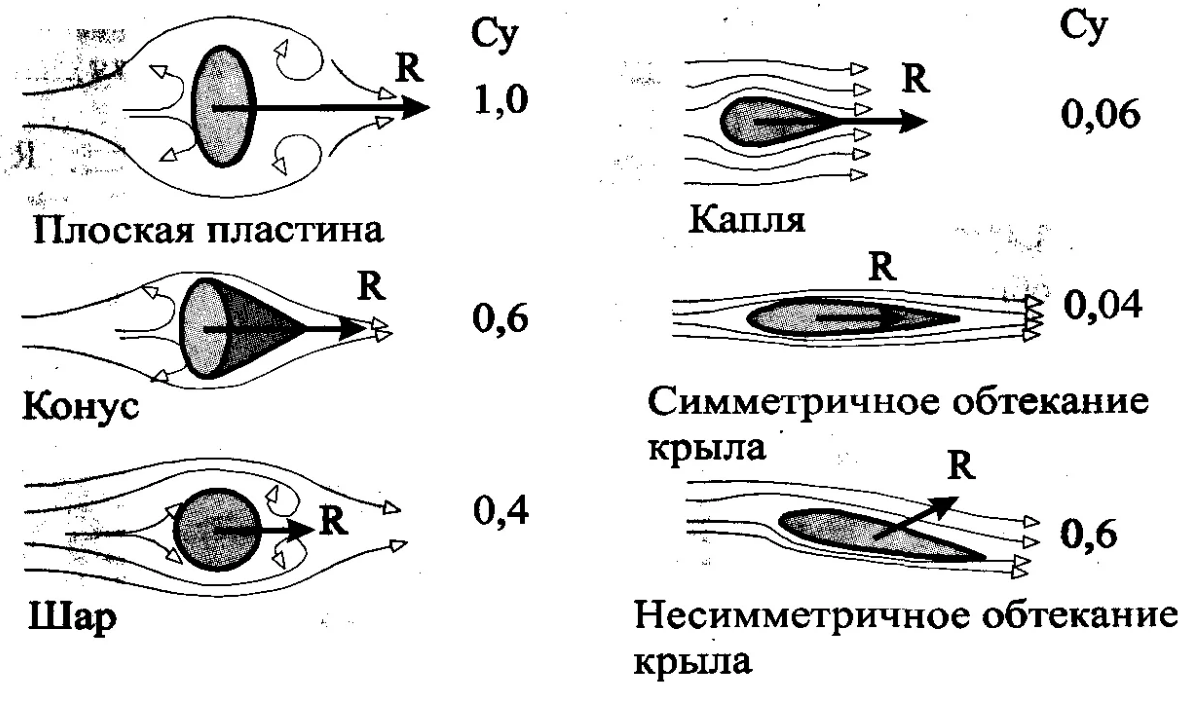

Рис. 19. Режим обтекания фюзеляжа с отрывными струями, под которыми создаётся зона нулевого сопротивления полёту. Всё сопротивлении фюзеляжа равно аэродинамическому сопротивленю шара в его носовом обтекателе. И сопровоодительные иллюстрации из учебников на тему сравнения сопротивления при обтекании воздухом различных тел .
Теперь рассмотрим поведение отрывных турбулентных зон при крыле с большим углом атаки (см.рис.20).
Сначала необходимо проследить траекторию отрывного потока над застойной зоной до момента встречи с потоком из под крыла самолёта. Так как профиль лобового обтекателя крыла считаем симметричным цилиндрическим, то и отрывные струи имеют равную мощность и траекторию, то есть тоже симметричны.
Для горизонтального крыла мы уже получили симметричный двусторонний отрывной пузырь с замыканием струй на крыле в одинаковых местах.
При придании крылу большого угла атаки картина отрывных струй меняется. При этом размеры «Отрывных пузырей»= «Застойных зон» над и под крылом начинают разительно отличаться по объёму.
В итоге в качестве «фиктивного тела» получится очень сильно распухшее крыло со значительным уплощением нижней плоскости по сравнению с огромным куполом отрывного пузыря на верхей плоскости крыла. Интересно, что эквивалентный виртуальный профиль «фиктивного тела» на большом угле атаки крыла с раздутыми отрывными пузырями на верхней плоскости крыла удивительно похож на известный летательный аппарат ЭКИП. (см. рис.21)
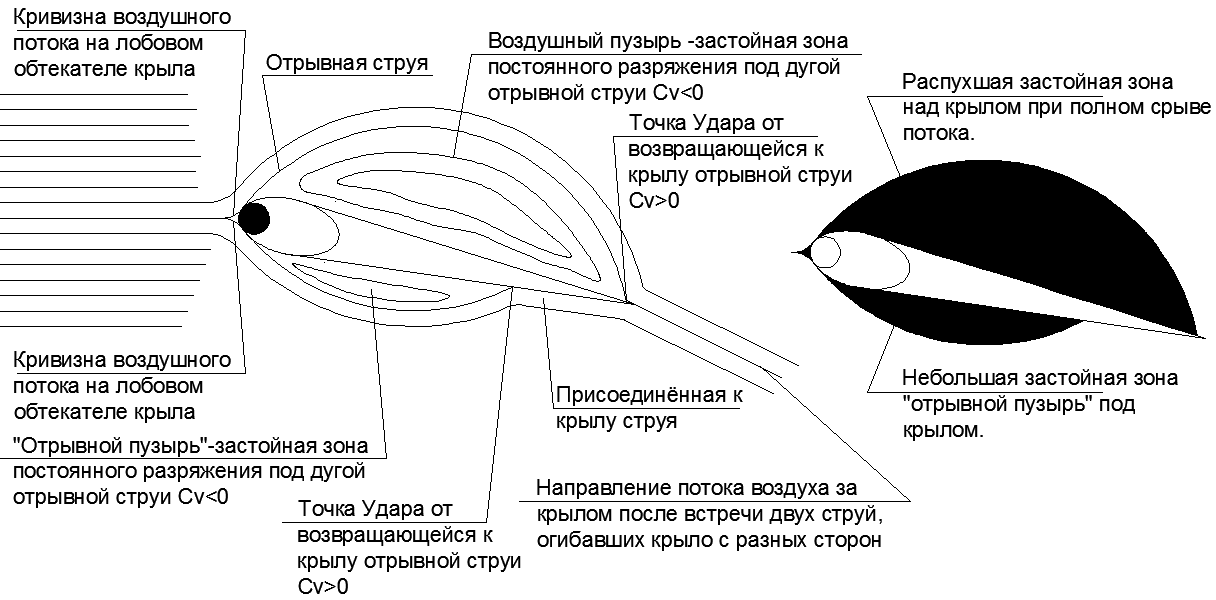
Рис.20. Профиль крыла с отрывов потоков на плоскостях крыла при большом угле атаки и его «Фиктивное тело».



Рис.21. Экраноплан ЭКИП. Макет перспективного образца Экраноплана и действующая уменшенная модель Экраноплана (так и не взлетевшая из-за остановки проекта).
То есть в Экранолёте ЭКИП предлагалась вполне здравая мысль по контролю застойной зоны в задней «теневой» части корпуса, что позволяло осаживать отрывную струю на крыло в верхней части купола, что даёт большую подъёмную силу и уменьшает аэродинамическое сопротивление полёту.
Выходит, что автор ЭКИПа был не таким уж и выдумщиком, предлагая в качестве летательного аппарата такую бегемотоподобную конструкцию.
Правда летать ЭКИП должен не очень быстро и на больших углах атаки исходного тонкого профиля (около 15 градусов), с соответствующим высоким лобовым сопротивлением.
Огромный объём грузового пространства в таком летающем крыле с лихвой может скомпенсировать некоторое ухудшение аэродинамики. При этом конструктивно безфюзеляжный Самолёт-Крыло выглядит гораздо привлекательней, чем традиционный самолёт с разделением функций тонкого «несущего крыла» и «грузо-пассажирского фюзеляжа». Вот только для стабильного полёта ещё придётся добавить длинную балку для размещения хвостового оперения, как на гигантском летающем крыле АНТ-20 «Максим Горький».
Значительное расширение крыла (увеличение хорды) делает Самолёт типа ЭКИП ещё и ярко выраженным Экранопланом по своим аэродинамическим свойствам при полёте вблизи земли. Так при полёте на экране «фиктивное тело» крыла с большим углом атаки трансформируется в странный утюг, где маленький носовой клюв зоны торможения на крыле раздувается до размеров огромного застойного клина под крылом (см.рис.22).
Образование такой мощной застойной зоны под крылом с большим углом атаки хорошо видно на стопкадре (см.рис.22-2). Сссылка на видео целиком www.youtube.com/watch?v=Sd4ycAtYcJA. Хорошо видно в трёх ракурсах одновременно как дымовые шнуры от двигателя огибают лобовой обтекатель снизу вверх и на равном удалении от крыла огибают всю плоскость крыла сверху.

Рис.22. Профиль крыла при полёте над экраном при большом угле атаки и его «Фиктивное тело».
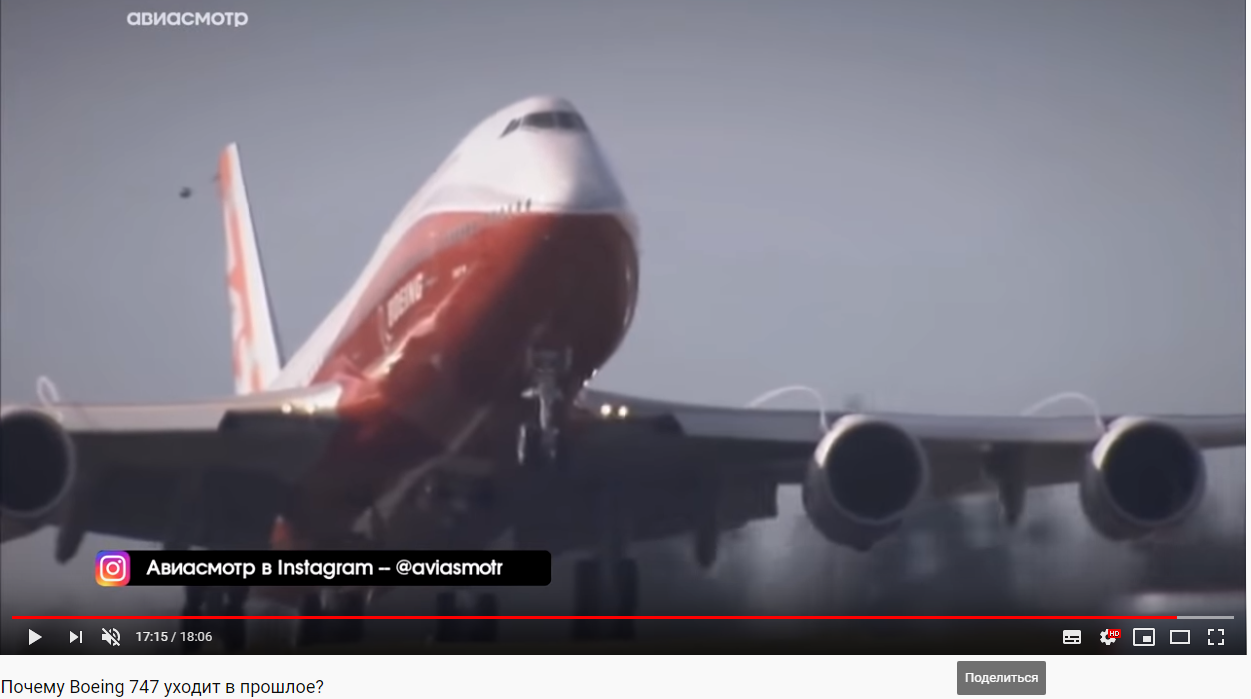
Рис.22-2. Дымовые шнуры от двигателей, затекающие из под крыла Боинг-747 в момент отрыва от ВПП на взлёте.
Внутрь этого остроносого утюга можно разместить как профили Экранолётов ЭКИП и ВВА-14 (Бартини), или сверхтолстое крыло как у АНТ-20 «Максим Горький».
Самолёты с очень толстым крылом были популярны в 1930-х годах в СССР, когда был создан самый крупный довоенный самолёт АНТ-20 «Максим Горький». У этого самолёта крыло было на столько толстым и широким, что в корневых отсеках крыла помещалось несколько кают, где человек ходил в полный рост (см. Рис.16.).
Правда, летал этот монстр с крейсерской скоростью всего 198км/ч (максимум 220км/ч).
Если у АНТ-20 чуток укоротить концевые участки крыла, оставив только центральную наиболее толстую часть, то самолёт станет похож на более поздний Экраноплан «Каспийский Монстр» Ростислава Алексеева.
Интересно сравнить близкие по размерам «Максим Горький» из 1930-х с «Каспийским Монстром» из 60-х (см.таб.5)
Таб.5. Сравнительные характеристики самолёта АНТ-20 «Максим Горький» 1934г. и Экраноплана КМ «Каспийский Монстр» 1966г.

В таблице представлены справочные данные, которые надо как-то интерпретировать.
Пойдём сначала простым путём прямого сравнения однородных цифр делением друг на друга.
Масса максимальная: 544/42= 13 раз
Площадь крыла: 662/486=1,36 раза
Удельная нагрузка на крыло: 13/1,36=9,5 раз
Скорость крейсерская: 430/198=2,17 раза
Различие скоростных напоров на крейсерской скорости: 2,17^2= 4,71раза
Мощность энергоустановок: (10*1300*9,81*430/3,6) /(8*900 000*0,735)=28,8 раз
Грузоподъёмность с учётом топлива: 304/(42-28,5)= 22,51.
Практическая дальность: 1500/1200=1,25
По соотношению топливной экономичности АНТ-20 = 7150/(1200*6)=0,993 л/(т*км)
Прожорливость КМ не известна, но можно её оценить через мощность и скорость.
При расчёте на удельный расход по справочной прожорливости 0.8кг/(кгс*ч) для двигателя ТРД ВД-7.
Расход на форсаже при разгоне с воды 10*13000*0,8=104 000кг/ ч
Если учесть длительность крейсерского полёта на экране только с двумя работающими моторами из десяти имеющихся для разгона и выхода на Экран, то экономичность повысится.
Для крейсерского полёта с двумя двигателями 2*13 000*0,8=20 800кг/ ч
Время полёта 1500/430=3,5часа
За полёт на максимальную дальность 1500км КМ сожрёт не менее 104*0.5+3,5*20,8=100тонн топлива.
А полезная нагрузка составит около 200 тонн.
Топливная экономичность КМ получится 100 000/(1500*200)=0.333 л/(т.км).
Выводы из полученных соотношений:
1. По топливной экономичности КМ может в оптимистичном варианте оказаться в 3 раза экономичнее, чем АНТ-20.
Сейчас у современного авиалайнера Аирбас А380 предусмотрена грузовая модификация A380F с возможностью перевозить груз до 150 тонн на расстояние до 10 370 км. Максимальная взлётная масса — 560 тонн (масса самого самолёта — 280 тонн). Расчёт экономичности для грузовой версии делаем из этих показателейдаёт 130тонн топлива 150 тонн груза на дистанцию 10370км: 130000/(150*10370)=0,0835 л/(т*км).
В пересчёте на пассажиров показатель другой: «Среди больших лайнеров самый экономичный — три литра топлива на одного пассажира на сто километров (54 морских миль) пути. По заявлениям Airbus[5], в расчёте на одного пассажира A380 сжигает на 17 % меньше топлива, чем «современный самый большой самолёт» (по всей видимости, имеется в виду Boeing 747). „
То есть при проверочном пересчёте на 850 пассажиров с багажом и креслами получим показатель близкий к расчёту для грузовой версии.
Выходит, что мы не только стали в 4-5 раза быстрее летать за последние 80 лет, но и по топливной экономичности улучшились более чем в 10 раз от АНТ-20 и в 4 раза от Экраноплана КМ. Хотя всего 20 лет назад наши аэробусы летали в 5 раз быстрее, чем АНТ-25. Недавнее снижение скорости в пассажирской авиации вызвано борьбой за топливную экономичность полёта.
2. Крейсерская скорость у КМ сделана столь высокой вынужденно, так как на меньшей скорости он просто не сможет лететь на экране. Условие полёта на экране- это выполнение неравенства «Скоростной напор» > «Средняя нагрузка на крыло», то есть
Pv= 8560Па при 430км/ч(120м/с) > 544000*9,81/662,5=8055Па.
3. Полётная безопасность тихоходного Самолёта-Гиганта из 30-х сильно лучше, чем у избыточно скоростного экраноплана из 60-х, почти неуправляемо несущегося среди тихоходных судов и вездесущих водных птиц.
4. Стоимость эксплуатации водоплавающих по морю экранопланов значительно дороже, чем для сухопутных высотных самолётов. Это связано с избыточным количеством двигателей, нужных только для старта с воды и выхода на экранный полёт, а также из-за чрезвычайной агрессивности морской воды при воздействии на двигатели и конструкции экраноплана при полёте в облаках брызг от близких морских волн.
5. Для Экраноплана КМ легко считается качество крыла при полёте на двух двигателях, равное отношению их тяги к весу самого экраноплана К=544/(13*2)=20,9. Таким образом, аэродинамическая эффективность большого и тяжёлого Экраноплана находится на уровне экономичность лучших современных крупных самолётов с качеством планера порядка К=18-20.
6. Загадкой для меня остаётся трёхкратный разрыв по экономичности Экраноплана КМ с Аэрбас 380F: Почему при равном качестве планера у Аэрбаса в 4 раза лучше топливная экономичность?
Или вся тайна кроется в жуткой прожорливости старых советских турбореактивных двигателей в сравнении с современными турбовентиляторными двигателями высокой степени двухконтурности?
Прошёл ровно год после первой пуликации на Хабре моей статьи (4.02.2019) про объяснение подъёмной силы крыла без уравнения Бернули.
Статья за год набрала боле 41 тысячи просмотров и заняла лидирующее положение в поиски Яндекс на запрос «подъёмная сила крыла», оказываясь в верхней части первой страницы сразу за определением из Википедии.
Так же в личных сообщениях мне было дано множество ценной информации и крайне важных критических замечаний.
Я не буду править ранее написанные части, но проведу разбор некоторых ошибочных заявлений, которые мною были оттиражированы из таких же ошибочных заявлений учебников.
Замечание 1.
Основным замечанием оказалось то, что я ошибочно привёл и неправильно истолковал картинки наглядных сравнений аэродинамических сопротивлений различных тел вращения полёту.
Так я считал это сопротивление соответствующим сопротивлению Сх для поляр самолётов, а на картинке из какого-то учебника (рис.19 во второй части) вообще указано ошибочное обозначение Су вместо Сx.
Мне же объяснили, что на самом деле для отдельных тел вращения будет правомочен коэффициент Cd, который связывает поперечное сечение (мидельное) продуваемого объекта с оказываемым ему сопротивлением скоростным напором.
Величина Cd у лучших гоночных машин не опускается ниже 0,27.
При этом для веретёнообразных тел и профиля крыла без подъёмной силы коэффициент лобового сопротивления заявляют до 0,06..0,04, что для показателя Dх не достижимо никогда.
Такое низкое Су, как 0,06...0,04, не является прямым обманом, но вводит в заблуждение из-за утаивания обстоятельств и нюансов расчёта. Так величина Cd рассчитывается из отношения к поперечному сечению (миделю), а величина Cх рассчитывается из соотношения к наибольшей площади крыла в вертикальной проекции, то есть к наиболшей площади крыла в продольном направлении к действующей силе сопротивления.
Так на красочных картинках, демонстрирующих обтекаемость различных тел в полёте, начинают некорректно сравнивать «Длинное» с «красным», то есть сравнивать величины в несравнимых размерностях.
Реальные же значения лобового сопротивления Сd, отнесённого к сечению по “миделю», cмотрите в таблице ниже.
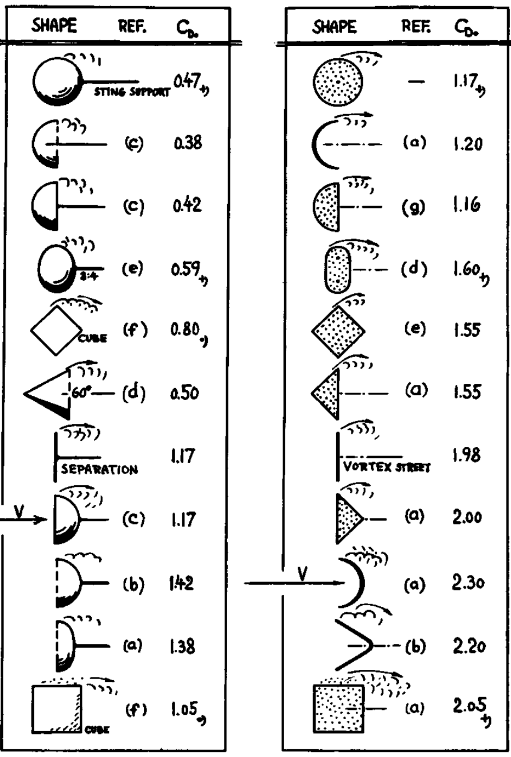
Таб. Величины лобовых аэродинамических сопротивлений Сd тел различной формы.
Левая таблица- тела вращения. Правая таблица- балки заданного сечения.
Замечание 2.
Хабр- отличный ресурс для публикации научно-технических статей разного профиля, но его правила дают удивительно широкие полномочия «троллям-негативщикам», которые своими дизлайками загоняют карму автора в глубокий минус, лишая его возможности как отвечать на критические замечания, так и делать новые публикации своих статей. Об этой особенности Кармы на Хабре есть даже опубликованные статьи на самом Хабре.
В результате падения моей Кармы ниже -30 я оказался отрезан от права комментировать свои же статьи, а так же лишен права на публикации.
Исключением является эта статья по аэродинамике, где мне каким-то чудом оставлено право на редактирование.
Этой «дырой возможности» я и воспользуюсь для публикации новой части статьи в обход отрицательной кармы.
Все ваши замечания и пожелания вы можете обращать мне в «личные сообщения» на самом Хабре или по адресу моей е-почты imoninpgd@gmail.com, также указанной и в начале каждой моей статьи.
Я всегда с удовольствием отвечаю на личные сообщения с конструктивной критикой в вежливой форме.
Как оказалось, расссмотренные в первой части тонкие выпукло вогнутые радиусные крылья сейчас активно используются в качестве поворотных лопаток в больших аэродинамических трубах (см.рис.23, 24)
На рисунке ярко видно, что для поворота потока используют именно такие тонкие лопатки, как и в моей статье.
Нет никаких сомнений, что конструкторы этих поворотных лопаток знают о тех механических нагрузках, которые испытывают данные лопатки от набегающего на них потока.
Также несомненно легко замерить давление на лопатки от искривлённого потока воздуха как на выпуклой, так и на вогнутой части этих лопаток. Причём замер давлений можно осуществить как для одного потока по толщине, так и для для одной лопатки с разных сторон.
Полагаю, что людям, имеющим доступ к АДТ ЦАГИ, не составит больших сложностей снять тензодатчиками давление с лопаток направляющего аппарта АДТ во время одного из текущих экспериментов.

Рис.23. Профиль аэродинамической лопатки, применяемой в современной аэродинамической трубе в качестве наборного поворотно-спрямляющего устройства в воздушном тракте АДТ.
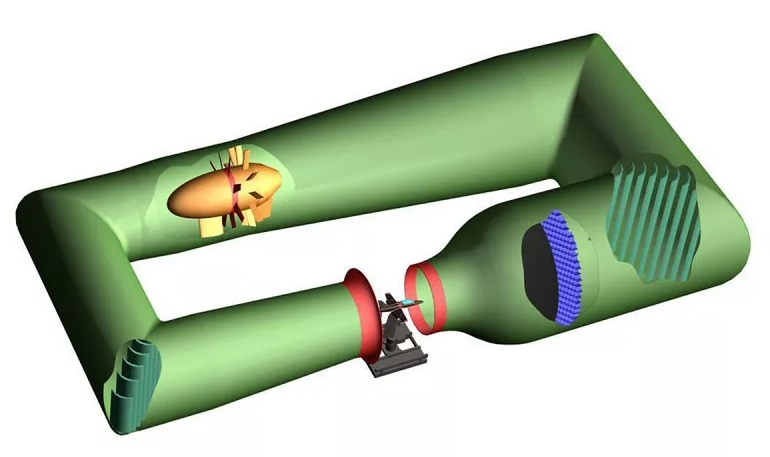
Рис.24.Расположение поворотных лопаток в тракте АДТ в 3Д-визуалищзации.
На фото (ри.25) изображены профили рабочих лопаток ротора газовой турбины из некого учебник по «Гидрогазодинамике», где рассматриваются элементы конструкции энергетических паровых и газовых турбин.
Эти лопатки практически точно повторяют профиль тонкого изогнутого выпукло-вогнутого крыла, описанного в теоретической 1-й части этой статьи, точно также как совпадают методики расчёт нагрузок на лопатки от потока газа в этих учебниках по «Гидрогазодинамике» с изложенной методикой в 1-й части этой статьи.
Отличительной особенностью работы лопаток ротора турбины заключаются в том, что при огибании газом поверхности лопаток сам газ не меняет плотности и температуры, но лишь плавно меняет направление вектора скорости потока газа, не меняя скорости газа по модулю, если рассматривать поток газа в координатах с привязкой к самой лопатке турбины. То есть условия работы отдельной лопатки ротора турбины практически точно воспризводят условия работы одиночного тонкого изогнутого крыла в свободном воздушном пространстве.
Удивительно то, что изложенное мною в статье давно известно и широко используется в прикладных расчётах в «Гидрогазодинамике» при конструировании газовых турбин как для энергетики так и для двигателей самолётов, при этом адепты «Аэродинамики» в упор не замечают эти расчётные и теоретические модели из «Гидрогазодинамики», считая «Аэродинамику» и «Гидрогазодинамику» разными науками с разными законами взаимодействия для совершенно одинаковых твёрдых крыльев с окружающей их одинаковой средой газов и жидкостей.

Рис.25. Профили рабочих лопаток газовой турбины и визуализация потока газов на них.
В период бурного развития авиации в 1930-х годах в погоне за высокими скоростями неожиданно проявилось удивительное явление, названное Флаттер, когда на определённой скорости самолёта внезапно возникают нарастающие крутильно-изгибные колебания крыльев, за несколько секунд приводящие к разрушению самолёта.
С этой проблемой разобрались конструктивными методами, увеличив крутильную и изгибную жёсткость конструкций крыла, но теоретические объяснения так и остались на уровне «Интуитивно-эмпирических решений», хотя академик Келдыш получил за эти решения Сталинскую премию.
В учебниках по аэродинамике (см. библиографию) я не обнаружил глав, объясняющих флаттер.
Таким образом, я буду давать объяснения явления Флаттера не опираясь ни на какую официальную теорию, а просто выводя следствия из теоретических положений, описанных в первой части статьи.
Как было описано в первой части, на лобовой обтекатель набегает поток, имеющий радиус искривления не менее
Rп=2*Rобт
Где Rобт – радиус скругления лобогого обтекателя крыла.
При этом толщина отклоняемого в каждую сторону от крыла потока равна Нп= Rобт.
Из геометрического построения следует, что угол вектора скорости отрывного потока при касании его обтекателя к направлению полёта равен
А=arccos(2/3)=48 градусов .
Вертикальная проекция скорости отрывного потока равна
Vп. верт=Vп* sin А=0,743*Vп.
То есть мы получили оценку сверху скорости по вертикали для отрывного потока, так как у нас ране уже был получен критерии предельной оценки для радиуса искривляемого потока Rп=2*Кобт
при толщине отклоняемого в одну сторону потока Нп=Rобт.
При дальнейшем движении над искривлённым профилем крыла отрывной поток с исходной энергией
Еп.верт.= Vверт.п^2*q*Rобт
должен погасить её за счёт работы разницы давления окружающего воздуха и давления на поверхности крыла под отрывным течением, то есть за счёт работы давления разряжения над плоскостью крыла.
Евозд= Нотр*Рвозд
То есть должно быть выполнено равенство Еп.верт=Евозд
Vверт.п^2*q* = Нотр* Рвозд
Высоту огибаемого пузыря без срыва потока с профиля:
Нотр= Vп.^2*q* Rобт /Рвозд
Подставляя выражение для Vп. верт=Vп* sin А
получаем:
Нотр= (Vп * sin А )^2*q* Rобт / Рвозд = Vп.^2*q* sin А^2* Rобт/ Рвозд
То есть при высоте профиля выше этой величины обтекание происходит без образования отрывного пузыря.
Если же величина горба профиля за лобовым обтекателем ниже величины Нотр, то обтекание профиля потоком происходит с образование воздушного пузыря с разряжением и застойным воздухом внутри, визуально обнаружимого по колебаниям шелковинок.
Дальше возникает вопрос длины застойного пузыря под отрывным течением.
Если считать перепад давления воздуха постоянным, то торможение потока воздуха будет равноускоренным, а кривая границы отрывного пузыря будет иметь вид параболы горбом вверх.
Время полного торможения потока по вертикали составит
T=V верт/А.верт
Где А.верт=Рвозд/(Rобт*q)
Получаем
Tпуз1=V верт/А.верт= V верт*(Rобт*q)/ Рвозд
Длина отрывного пузыря Lпуз1 до вершины составит
Lпуз1=Vп*Тпуз1= Vп* V верт*(Rобт*q)/ Рвозд= Vп *(Vп * sin 42)*Rобт*q/ Рвозд =>
Lпуз1=Vп ^2*q * sin А*Rобт / Рвозд
Из полученной формулы Lпуз1 для длины восходящей части отрывного течения над отрывным пузырём (или идеальным профилем) можно сделать вывод, что при некоторых значениях скорости полёта Vп и толщины лобового обтекателя Rобт может возникнуть ситуация, что величина отрывного пузыря
L пуз 1+2= 2* Lпуз1
может превысить ширину крыла Вкр.
Когда расширения отрывного пузыря достигает задней кромки крыла, а ниспадаюший отрывной поток уходит за заднюю кромку крыла, тогда под отрывной пузырь попадает воздух с высоким давлением из спутного следа.
После выравнивания давления в отрывном пузыре с атмосферой на отрывной поток перестаёт действовать разница давлений между атмосферой и пузырём над крылом. После чего отрывной поток отрывается от обтекателя и уже не может вернуться обратно на крыло, тем самым создавая полный срыв потока.
При скоростном горизонтальном полёте выше расчётной нормальной скорости для конкретного самолёта при таком срыве потока над верхней плоскостью крыла дальнейшие события развиваются в следующем порядке (см.рис.26):
— Отрывные течения формируют на крыле с малым углом атаки отрывные пузыри разных размеров, при этом общая равнодействующая подъёмная сила крыла Fк1= Fк.верх- Fк.низ, а крутящий момент относительно ЦТ имеет расчётную величину на рычаге L1
— При ускорении до Vф отрывноое течение над верхней плоскости крыла достигает задней кромки, а равнодействующа Fк2 становится больше расчётной Fк1. Также сильно возрастает крутящий момент на крыле от увеличения плеча L2 усиливая момент на пикирование.
— При срыве потока подъёмная сила от разряжения в верхнем отрывном пузыре пропадает.
— При резком исчезновении разряжения над верхней поверхностью крыла возникает мгновенное разгружение конструкций крыла только с одной стороны.
-На нижней плоскости крыла срыв потока ещё не происходит, а потому продолжает действовать значительная аэродинамическая сила вниз от развитого отрывного пузыря, которая по модулю многократно превосходит нормальную подъёмную силу крыла.
Таким образом, происходит резкая перегрузка крыла на изгиб в другую сторону, то есть вниз, с закручиванием крыла на кабрирование.
В результате самолёт резко проваливается вниз, задирая нос и теряя скорость.
При закручивании крыла задней кромкой вниз резко растёт угол атаки всего крыла, в результате чего резко усиливается торможение на поток воздуха, при этом происходит схлопывание отрывного пузыря, а подъёмная сила на нижней поверхности крыла резко меняет знак на подъём, выгибай крыло снова вверх.
При восстановлении нормального направления подъёмной силы крыло начинает резко изгибаться вверх, а момент от вновь созданной нормальной подъёмной силы скручивает крыло и разворачивает крыло со всем самолётом из кабрирования на пикирование.
Таким образом цикл замкнулся и пошёл на второй круг.
Самолёт уходит в разгон, восстанавливается обтекание без срыва потока по верхней плоскости крыла, и после нового достижения критической скорости срыв потока возникает снова, а изгибные перегрузки крыла со скручиванием повторяются.
Вот такая быстротекущая тряска со знакопеременными изгибами и скручиванием крыльев (при нагрузках в разы выше расчётных статических) неизбежно приводит к быстрому разрушению крыльев.

Рис.26. Фазы развития флаттера на крыле:
1) Нормальная подъёмная сила Fк1 до начала флатера, где площадь заштрихованного прямоугольника показывает равнодействующую сил давления на крыло от симетричны отрывных потоков.
2) Избыточная подёмная сила на крыле Fк2 при повышении скорости выше расчётной. От избыточной подъёмной силы Fк2 силы на сильно увеличеном плече L2 образуется сильный крутящий момент на пикирование незадолго до срыва потока с верхней плоскости и начала флаттера.
3) Срыв потока с верхней плоскости крыла при развитом флаттере. На верхней плоскости подъёмная сила исчезает из-за выравнивания давления с атмосферой. Некомпенсированная сила от нижнего отрывного пузыря создаёт перегрузку крыла огромной силой Fк3 в сторону земли, а крутящий момен на крыле резко меняется на кабрирование.
4) При резком увеличении угла атаки крыла набегающий поток воздуха гасит отрывной пузырь с пониженным давлением на нижней плоскости крыла, в результате чего подъёмная сила меняет направление на нормальное, то есть вверх, с востановлением крутящего момента на расчётное пикирование.
Именно такое циклическое быстро повторяющееся крутильно-изгибное колебание крыла на некой критической скорости Vф и называют Флаттером.
Разрушения крыла от Флатера можно избежать путём резкого усиления конструкций крыла. Именно такую рекомендацию на «интуитивно –эмпирическом уровне» дал Келдыш.
При этом усиливается не только прочность по величине выдерживаемых статических нагрузок на крыло, но также усиливается жёсткость крыльев на изгиб и кручение, что позволит понизить накапливаемую во взмахах крыльев энергию, тем самым сделав её ниже пороговой энергии разрушения крыла.
Для увеличения жёсткости на кручение лучше всего применять замкнутый контур типа «труба» или «короб». Более жесткие на кручение «короба» оказываются значительно тяжелей «ферм», применявшихся на тихоходных самолётах ранних конструкций.
В более поздних и продвинутых конструкциях самолётов замкнутым крутильным коробом оказывается вся внешняя толстая листовая обшивка крыла, при этом с применением внутри объёма крыла несущих балок и рёбер жёсткости ферменного или двутаврового типа. Использование листовой обшивки крыла в качестве несущего силового элемента резко увеличивает жёсткость конструкции с одновременным снижением веса всего крыла.
Кстати, в самодеятельном авиастроительстве с плёночной или тканевой обшивкой крыла и сейчас очень часто тонкостенные трубы применяют как основную несущую балку крыла.
Избежать появление флаттера на желаемой к достижению скорости можно за счёт изменения профиля крыла в сторону уменьшения радиуса лобового обтекателя Rобт, что приведёт к повышению величины пороговой скорости Vф для нового профиля крыла.
Согласно сделанных расчётов никак не получится избежать флатера совсем в горизонтальном полёте, но снизить его влияние для достижения предельных скоростных значений вполне возможно.
Таким предельным значением является скорость звук, после которой режим обтекания крыла резко меняется, а флаттер остаётся в дозвуковом скоростном диапазоне.
При сверхзвуковом полёте обе плоскости крыла информационно разделены, так как низкочастотные волны давления (звуковые волны низкой частоты с большой длиной волны) от циклических срывов потока не могут обогнать сверхзвуковое крыло и нарушить однородность воздушных масс перед летящим крылом.
Таким образом, даже если плоскости крыла работают в попеременном режиме полного срыва потока, то после перехода «звукового барьера» трясти самолёт резко перестаёт.
Как рассакзывают лётчики, после перехода звукового барьера после мучительной тряски внезапно наступает тишина.
Именно из-за принципиальной неустранимости флаттера летать на опасных флатерных трансзвуковых скоростях рекомендуют очень короткое время, что достигается быстрым разгоном до сверхзвука на полном форсаже, или быстрым торможением со сверзвука до уровня дофлатерной скорости.
Такими быстрыми проходами флатерного диапазона скоростей обеспечивается минимальная длительность воздействия вибрации от флаттера на конструкции самолёта.
При уменьшении радиуса лобового обтекателя Rобт само явление флаттера не исчезает полностью, но сдвигается в сторону более высоких скоростей.
Так в 1930-х для наиболее скоростных истребителей флаттер был актуален на скоростях 300-400км/ч, когда избытка мощности двигателя хватало разогнать небольшие облегчённые самолёты до критической скорости.
При снижении размеров Rобт на крыле были получены гораздо более скоростные и более высотные истребители, такие как МиГ-3 образца 1940г.
Но платой за скорость для новых скоростных самолётов оказалась меньшая подъёмная сила на низких скоростях, что потребовало бы больших скоростей при посадке.
Но увеличивать посадочные и взлётные скорости на грунтовых аэродромах нельзя!
Чтобы справиться с этой проблемой пришлось в конструкцию крыла новых скоростных самолётов специально для режима взлёта и посадки вводить дополнения в виде отклоняемых пластин — «закрылков» и «предкрылков». Закрылки и предкрылки резко поднимали подъёмную силу крыла на низких скоростях с большими углами атаки, но ухудшали качество крыла.
Так гонка за скоростью и борьба с флаттером привели к утяжелению крыла для упрочнения и усложнения крыла для обеспечения приемлимых скоростей влёта и посадки, что тоже дополнительно утяжелило самолёты.
Для сравнения можно оценить истребитель простой конструкции дофлатерной геометрии И-16 и более скоростной и сложный МиГ-3 (с предкрылками и закрылками в оснащении). Так при почти равной мощности мотора первый имел в полтора раза меньшую массу и при этом на 75-170 км/ч меньшую скорость (у земли 420км/ч и на высоте 470км/ч), чем более обтекаемы и скоростной, а потому более сложный и более тяжёлый МиГ-3 (у земли 495км/ч, на высоте 640км/ч).
Отношение максимальной скорости МиГ-3 и И-16 и составляет 495/420=1,18.
При этом согласно полученной формуле длина отрывного пузыря пропорциональна квадрату скорости, то есть увеличение скорости на 20% удлинит отрывной пузырь в 1,44 раза.
То есть для такого 20% приращения скорости без срыва потока и проявления Флаттера нужно либо расширить крыло в 1,5 раза, (что, как правило, конструктивно невозможно), либо уменьшить в те же полтора раза радиус скругления носового обтекателя и общую высоту профиля.
Именно таким образом решали проблему разгона МиГ-3, уменьшив толщину крыла по сравнению с И-16, при этом практически не изменив ширину крыла.
Такое снижение несущих балок крыла по высоте в полтора раза да ещё и при увеличении массы самолёта в те же полтора раза неизбежно потребует увеличения сечения наиболее нагруженных горизонтальных полок двутавровых балок приблизительно в 2,5-3 раза, что неизбежно приведет к заметному увеличению массы конструкции крыла в целом.
Сейчас современные дозвуковые аэробусы летают на скоростях 800-900км/ч, при этом не достигая критической скорости Vф, характерной для их профиля крыла. Низкое сопротивление потоку воздуха от тонкого крыла и отсутствие Флаттера на высоких скоростях влечёт за собой малую подъёмную силу при низких скоростях взлёта и посадки, что также требует установки развитой механизации крыла из комплекта закрылков и предкрылков, выдвигаемых из крыла вниз в режимах взлёта и посадки.
Полёт на высоких скоростях без флаттера у современных аэробусов достигается комбинацией технических приёмов, используемых в различных наборах на отдельных участках крыла (см.рис.26-2):
1. Толстая корневая часть имеет большую ширину и максимальную прочность, так что никакие срывы потока и тряска на «воздушных ямах» ей не страшна. На корневой трети крыла закреплён и тяговый двигатель. Именно эта наиболее широкая часть крыла создаёт наибольшую долю подъёмной силы крыла в полёте на крейсерской скорости на высоте 10км. Эта корневая часть имеет установочный угол профиля по отношению к фюзеляжу, равный углу атаки на крейсерской скорости.На корневой части установлены самые мощные выдвижные двухщелевые закрылки и предкрылки.
2. Средняя треть крыл имеет резкое сужение от корневой трапецивидной части. Также эта треть крыла плавно меняет угол атаки от установочного угла корня к нулю на расстоянии 2/3 от фузеляжа. Это изменение угла профиля по длине крыла называют «крутка крыла», что обеспечивает плавное снижение давления на крыле от корня к концу, тем самым снижая негативны эффект от концевого вихреобразования. У средней части такк же имеется механизация из предкрылков и закрылков.
3. Последняя треть крыла наиболее тонкая и не имеет полезной нагрузки при горизонтальном полёте на крейсерской скорости на высоте 10 км. Установочный угол последней трети крыла равен нулю (или близок к нулю). Роль узкой законцовки двойная: а.)Удлинитель крыла для снижения вихреобразовния на второй трети крыла. б) Удлинитель крыла для установки элеронов (рулей крена на крыльях) с максимальным плечём рычага. Установка элеронов исключает установку закрылков на дальнем конце крыла. Предкрылки на последней трети крыла для режимов взлёт-посадки также устанавливают.

Рис.26-2. Схематичный чертёж современного аэробуса, где можно чётко проследить три части крыла: толстую корневую с максимальным установочным углом атаки к фюзеляжу и мощной механизацией из прекрылков и двухщелевых закрылков (основная нагруженная часть в полёте), средняя переходная часть с переменной круткой профиля по углу атаки и полной механизацией из закрылков и предкрылков, крайня часть с нулевым установочным углом атаки и элероном на задней кромке для управления креном самолёта.
Замечательным моментом от проявления флаттера можно считать усиления внимания в СССР к научно-экспериментальному подходу к конструированию в авиации.
Невозможность объяснить на том теоретическом уровне явления флаттера вызвало острую потребность в моделировании полёта новой авиатехники в безопасных лабораторных условиях… В итоге к 1939 году в ЦАГИ была построена крупнейшая в мире на тот момент (вторая на сегодня) ародинамическая труба Т-101. Но ирония в том, что на момент ввода в эксплуатацию Т-101 уже морально устарела, так как её скоростные режимы (максимум 52м/с или 187км/ч) намного отстали от предельных скоростей в авиации на конец 1930-х, да и по размеру самолёты в эти годы уже переросли размеры экспериментальной зоны АДТ. В итоге на этой крупнейшей АДТ можно в реальных условиях испытывать только малоразмерные истребители и спортивные самолёты, да и то только в режимах низкоскоростных взлётов и посадок.
Аэродинамику современных самолётов и режимы течения воздуха вокруг них приходится изучать по отдельным фото самолётов с ярко выражеными туманными шлейфами (см.рис.27).
Добится такого эффекта в натурном виде в АДТ уже практически не возможно.
Данное явление называется Эффект Прандтля — Глоерта — конденсация атмосферной влаги позади объекта, движущегося на околозвуковых скоростях. Эффект чаще всего наблюдается у самолётов, но бывает он заметен и на более низких скоростях даже у автомобилей. Так в условиях очень высокой относительной влажности эффект можно наблюдать и при намного меньших скоростях, например на аэродинамических элементах автомобилей во время гонок Формула-1 в дождливую погоду.
У сверхзвуковых самолётов этот эффект также наблюдается, но при этом демонстрирует совсем иную картину туманных зон разряжения, чётко ограниченных линиями фронтальных ударных волны на лобовых поверхностях крыла и замыкающих волн разрежения при сходе с задней кромки крыла. (см.рис.28)

Рис.27. Полёт современног истрибителя с выпущеной механизацией на больших углах атаки с малой скоростью. Зоны разряжения над крылом выражены интенсивным выпадением тумана, под крылом зоны повышенного давления без образования тумана. Направление движения воздушных потоков под крылом самолёта хорошо отслеживается по туманными шнурами от подвешенных снизу крыла ракет.


Рис.28. Сверхзвуковой полёт с выраженными зонами выпадения тумана от конденсации атмосферной влаги ( Эффект Прандтля — Глоерта). Верхний снимок — при пролёте над переувлажнённым воздухом над морской поверхностью. Нижний снимок- полёт под облаками в условиях влажности близкой к 100%.
Сверхзвуковой полёт происходит по тем же законам физики и в той же среде, что и дозвуковой полёт, но существенным и крайне значимым различием является нераспространение волн плотности воздуха (звуковых волн) вперёд по ходу сверхзвукового летательного аппарата, что обеспечивает отсутствие влияния возмущённого воздуха из спутного следа на структуру воздушных масс перед крылом летящего самолёта. Это ограничение даёт резкое упрощение в понимании физических процессов взаимодействия крыла с воздухов при сверхзвуковом полёте.
Рассмотрим полёт крыла через идеальный невязкий газ со сверхзвуковой скоростью.
Последуем примеру учебника и рассмотрим взаимодействие идеальной тонкой пластины нулевой толщины с воздухом на сверхзвуковой скорости Мк>1 (Vк>Va).
Угол наклона пластины к скорости примем Ак.
Так как газ идеальный, то есть невязкий, то заторможенный пограничный слой отсутствует и трением между молекулами воздуха по поверхности пластины пренебрегаем.
Тогда летящая пластина с углом Ак к скорости может быть воспринята воздухом как твёрдая поверхность поршня, толкающая воздух перед собой. При этом скорость толкания воздуха в тангенциальном направлении к скорости полёта составит
Vт=Vк*sin Ак.
Так как угол Ак малый, то величина перпендикулярной скорости Vт будет много меньше сверхзвуковой. В таком случае происходит достаточно обычное толкание воздуха пластиной, движущейся с малой постоянной скоростью короткий отрезок времени, равный
Тт=Вк/Vк
Где Вк — ширина пластины в направлении полёта.
Зона влияния этого уплотнения воздуха над пластиной не превышает дальности распространения звуковой волны от каждой точки плпастины за время пролёта пластины Ттi через эту точку неподвижного воздушного пространства. Таким образом, форму этой зоны над пластиной можно ограничить фронтом звуковой волны или конусом распростронения звука в перпендикулярном к скорости Vк направлении за время Тт (конус Маха).
Угол фронта возмущения в воздухе от движения пластины к скорости полёта пластины будет равен
Аа=arctan( Va/Vк)= arctan (1/Мк)
То есть при скорости Vк=Vc наклон фронта волны звукового уплотнения составит 45 градусов.
При этом нам из опытов и шлирен фотографий явно видно, что ударный фронт на скорости 1М перпендикулярен скорости полёта, а на более высоких скоростях отклоняется назад по закону
Аударн= arctan (1/Мк)
То есть угол наклона фронта ударной волны от крыла при 1М будет равен 45 градусов.
При этом скорость удаления фронта звукового возмущения от крыла равна скорости полёта крыла, что описывается следующей геометрической картиной:
Катеты прямоугольного треугольника равны (скорость полёта равна скорости звука перпендикулярно крылу), а гипотенуза- это фронт ударной волны.
При скорости в 2М катеты будут уже иметь отношение 2:1, а угол наклона фронта составит величину
Аударн= arctan (1/2)=26,6 градуса
Такое различие в геометрии ударной волны на лобовых поверхностях и звуковых волн на плоскостях с малыми углами атаки говорит лишь о различии механизмов формирования ударных волн и звуковых волн.
Рассмотрим формирование звуковой волны в перпендикулярном направлении к скорости полёта на малых углах атаки Аа<< Аударн.
Для каждого момента пролёта пластины в данной точке неподвижного воздушного пространства существует своя величина удаления фронта звуковой волны от пластины
Lai=Ттi*Va
А величина поджатия воздуха в элементарном цилиндре с высотой Lai составит
Lтi =Ттi*Vт
В любой момент времен горизонтального полёта для плоской пластины Vт= const
Так как процесс быстротекущий, то воздух в зоне сжатия-разряжения меняет температуру за счёт совершаемой работы на крыле, но не успевает нагреться или остыть при теплообмене со средой, то есть протекает по адиабатическому закону с показателем адиабаты к=1,4 для воздуха
Р/Ро=(Vo/V)^1,4
При таком режиме движения толкающей поверхности у воздуха в зоне сжатия под фронтом звуковой волны появляется уплотнение, величина которого связано постоянным соотношением
Рк= Ро* /(1-Lт/La)^к=Ро/(1-Vт/Vа) ^k= Ро/(1- Vк* sinАк /Vа) ^k =Ро/(1-Мк* sinАк) ^k
Тогда изменение давления будет равно
dPк= Pк-Ро= Ро/(1-Мк* sinАк) ^k — Ро
Величина создаваемого избыточного давления постоянна по всей площади пластины, так как ситуация тождественна во всех соседних сечениях (см рис.29)

Рис.29. Схема продвижения плоской пластины на сверхзвуке через элементарный срез неподвижного воздушного пространства.
Период взаимодействия Тт определяет частоту генерируемой звуковой волны ( период полуволны), а интенсивность волны определяет проекция пластины на перпендикуляр к скорости
Нк=Вк* sinАк.
То есть, чем шире плоскость крыла, тем более низким и глухим будет звук ударной волны. И чем больше угол атаки крыла, тем больше сила звука. Это подтверждается наблюдением, что:
— пули над головой «свистят»- высокий тон 4-5кГц при малой длине самой пули (около2-3см) и короткой длине генерируемой волны ( длина волны 5-8см),
— Широкие лопасти пропеллеров турбовинтовых самолётов «гудят» с частотой около 90-170Гц, более низкий тон из-за значительно большей ширины лопасти ( около 0,5м лопасть и длина волны около 1-2м) в сравнении с размером пули.
Желающие сравнить ощущения от звука на разных частотах могут сами послушать звучание акустического ряда по частоте
yandex.ru/video/preview/?filmId=1603185091132691213&text=частота%20звука&noreask=1&path=wizard&parent-reqid=1583526054883660-1838767931406704632600067-vla1-1828&redircnt=1583526069.1
Итого.
Так как известны жёсткие ограничения по ширине зоны влияния и перпендикулярной к направлению полёта скорости толкающей пластины, то выясняется, что у объёма воздуха внутри конуса сжатия величина сжатия в разных сечениях одинакова.
При этом на плоскую пластину по всей площади давит одинаковое прибавочное давление dP.
Данное рассуждение верно и для пластины с отрицательнным углом –Ак на теневой от потока стороне пластины. Только вместо избыточного давления на ней будет разряжение на величину dP.
Простейший расчёт для плоского крыла на сверхзвуковой скорости Мк=1 даёт подъёмную силу на каждую сторону поверхности (давление) на уровне моря более 150кг/м.кв на каждый 1 процент уклона плоскости (100%*Нк/Вк), или более 300кг/м.кв при суммировании двух сторон идеально плоского тонкого крыла.
То есть уже при величине уклона крыла 2% (или 1,2 градуса угла атаки) обеспечивается необходимая современному истребителю удельная подъёмная сила на крыло в размере 500-600кг/м.кв при давлении атмосферы на уровне моря.
Для обеспечения манёвра с перегрузкойи в 10g в плотных нижних слоях атмосферы достаточно угла атаки на сверхзвуке 1,1М всего в 6,5 или 9 градусов (для Су- 57 и Су-35 соответственно).
А вот в разреженных слоях атмосферы уже на высоте 10км такие запредельные перегрузки становятся практически не реализуемы, так как для торможения с ускорением 10g пришлось бы практичеси ставит весь самолёт перпендикулярно потоку.
На больших высотах плотность воздуха и давление соответственно падают, что требует кратно больших углов атаки при той же сверхзвуковой скорости, или требует резкого роста скорости для компенсации падения давления воздуха в атмосфере и сохранения приемлемых углов атаки.
Именно с этим связанны столь высокие скорости истребителей (до 2,5Мах) на высотах 25км, где давление воздуха падает до 2,5% от величины на поверхности моря. И даже на таких скоростях углы атаки в разреженном воздухе приходится поднимать до критических 10-12градусов.
Данные расчёт можно проверить на примере сравнения двух практически одинаковых по большинству параметров самолётов Су-35 и Су-57. Они почти совпадают по массе, габаритам и тяге двигателей. Из массо- габаритных характеристик у них отличаются только площадь крыла и, как следствие, максимальная удельная нагрузка на крыло (см.Таб. Бис.30)

Рис.30 Таблица сравнения технических характеристик самолётов Су-57 и Су-35. Жёлтым указан сильно различающийся параметр в геометрии самолётов, а зелёным указаны последствия в изменениях ТТХ от модели к модели.
Результатом такого различия по удельной нагрузке на крыло оказывается увеличение: Максимальной скорости на сверхзвуке, максимальной высоты полёта, максимальной сверхзвуковой скорости без форсажа и максимально дальности полёта.
Попробуем получить эти выигрыши из полученых расчётных зависимостей подъёмной силы плоского крыла. Ниже приведены результаты расчётов в таблице, где попарно рассматривается на одном эшелоне с одинаковой скоростью самолёты Су-57 и Су-35.
Интересно отметить, что с ростом высоты полёта роль разряжения над крылом снижается, а роль сжатия становится доминирующей, достигая более 80% подъёмной силы на максимальной высоте полёта (см. рис.31. столбцы с показателями dP над и под крылом). Тогда как на уровне земли разряжение и сжатие вносят практически одинаковый вклад в создание подъёмной силы крыла на сверхзвуке.

Рис.31. Таблица сравнения аэродинамических характеристик самолётов Су-57 и Су-35. Внизу дополнительно указана строчка с характеристикой полёта американского самолёта разведчика «Чёрный дрозд» SR-71на скорости 3,2М на высоте 25 км.
Внизу таблицы отдельной строчкой показан пример максимальных полётных характеристик американского самолёта разведчика «Чёрный дрозд» SR-71, который по компоновке ближе к Су-57, а взлётные нагрузки на крыло ближе к СУ-35. Особенностью SR-71 является масса топлива на борту, составляющая 60% при влёте, тогда как у наших истребителей взлётный запас топлива всего 30% от максимальной взлётной массы. Таким образом, за время полёта нагрузка на крыло SR-71 изменяется от состояния хуже Су-35 в начале и до лучше Су-57 в конце полёта.
Интересно как отразилось на экстерьере истребителя Су-57 увеличение площади крыла на 32%.
Так если Су-35 выглядит эффектным самолётом с выраженным делением на крылья с явно отеделённым хвостовым оперением и агрессивным клювом наклонного к плоскости крыла фюзеляжем с кабиной экипажа, то облик Су-57 выглядит скучным плоским летающим блюдцем со слившимися в единый диск крыльями и хвостовым оперением. Су-57 эффектно выглядядит только в виде с верху, тогда как Су-35 выглядит крайне эффектно с любого ракурса (см. рис.32 -35)


Рис.32. Сравнение экстерьеров Су-35 (вверху) и Су-57(внизу). Заметно сильное уплощение Су-57 в профильной проекции, в сравнение с «крючконосым» Су-35.


Фото. 33. Сравнение вида Су-35 (вверху) и Су-57(внизу) в полёте. Явно выраженный наклон вниз передней части фюзеляжа у Су-35 говорит о больших углах атаки крыла в большую часть времени полёта, чтобы в этом положении фюзеляж находился горизонтально к скорости, тем самым минимизируя сопротивление полёту. У Су-57 фюзеляж вообще не выражен, при этом носовая его часть с кабиной является продолжением корневых наплывов крыла. То есть в борьбе за высокую сверхзвуковую скорость без форсажа лобовая проекция самолёта была минимизирована так, что фюзеляж редуцировался до утолщения крыла в корневой его части.
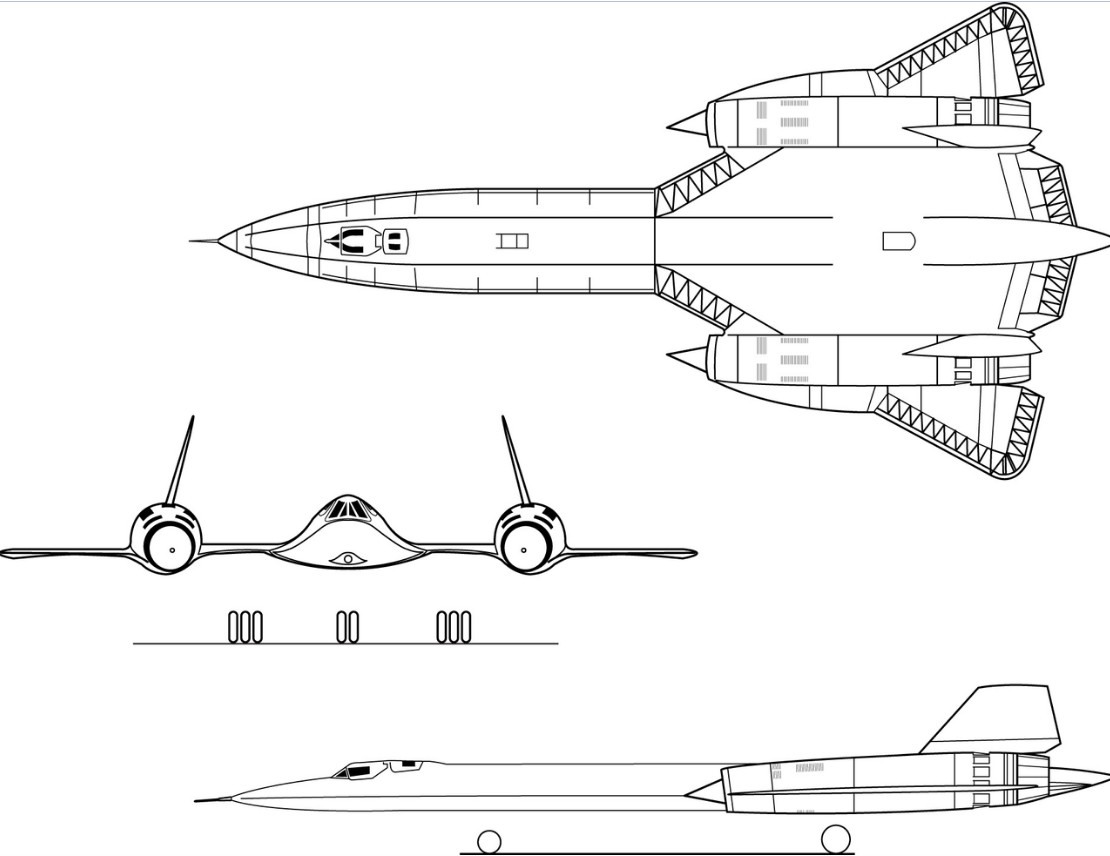

Рис.34. Сравнение экстерьеров «Чёрный дрозд» RS-71 и Су-57(внизу). Заметно сильное внешнее сходство этих очень разных самолётов в борьбе за высокую сверхзвуковую скорость в длительном режиме.


Рис.35. Внешний вид сверзвукового высотного самолёта-разведчика США «Чёрный дрозд» RS-71
Случай с ломаной пластиной характерен для тонкого участка лобовой кромки крыла, которую по конструктивным причинам невозможно сделать абсолютно тонкой и абсолютно острой, что приводит к появлению технически исполнимого достаточно большого по величине угла на лобовом обтекателе или на подвижном предкрылке. Местный угол профиля на предкрылке может быть в разы больше общей относительной толщины крыла. При общей относительной толщине крыла у современного истребителя около 5% (150мм при ширине крыла 3м), то на предкрылке шириной в 500мм и толщиной в корне в те же 150мм относительная высота элемента составит уже 150/500=30% (16 градусов)
Именно на этом клине возникает столь характерная для сверзвукового полёта ударная зона с формированием узко направленой ударной волны вдоль границы конуса маха.
Формирование волны высокой плотности от клинового обтекателя в границах конуса Маха создаёт интенсивное разряжение над крылом внутри конуса Маха, когда расширение профиля к середине крыла переходит в обратный уклон к задней кромке крыла.
Именно эту зону резкого разряжения и адиабатного охлаждения над крылом внутри конуса Маха видно на фотографиях, где образуется клиновидное конденсационно-туманное облако над обеими сторонами крыла, летящего на сверхзвуке самолёта. (см.рис 28).
Согласно расчёту ( см таб.рис.31) на малой высоте у земли в плотных слоях атмосферы полёт на сверхзвуке идёт на сверхмалых углах атаки (менее одного градуса), что обеспечивает зоны отрицательных углов и сильного разряжения (как следствия) на задней кромке крыла с обеих сторон крыла. Именно эти малые углы атаки обеспечивают визуальную симметрию туманных конусов за истребителями на фотографиях, снятых с земли.
Распределение ударных волн от обтекателя по сторонам крыла можно регулировать изменением отклонения предкрылка, смещая атакующий угол в одну из сторон.
Таким образом, можно создать подъёмную силу на плоском крыле даже при нулевом угле атаки, управляя лишь степенью асимметрии расположения клиновидного лобового обтекателя к встречному потоку. При этом на лобовом обтекателе с большим углом наклона к потоку возникает значительная подъёмная сила.
Теоретически можно добиться одностороннего выпадения тумана в конусе Маха даже на сверхзвуке, но при этом придётся разгрузить одну из плоскостей крыла, сделав её абсолютно плоской и горизонтальной в полёте. При этом на острый предкрылок сваливается избыточная нагрузка от веса самолёта, что перегружает отклоняемый клиновидный предкрылок, предъявляя излишне высокие прочностные требования к этому сравнительно небольшому элементу крыла. Поэтому на сверхзвуке предкрылок выставляют в основном в нейтральное положение к скорости, давая равномерную распределённую нагрузку по всей площади крыла с обеих сторон.
В итоге формируется суммарная подъёмная сила крыла, состоящая из нескольких частей, количественно равное числу граней на плоскостях сверхзвукового крыла, включающие в себя и отклоняемые элементы предкрылков и закрылков.
В момент окончания прохода крыла через неподвижный воздух за его задней кромкой происходит резкое исчезновение воздействия крыла на окружающий воздух. Сжатое состояние под крылом сменяется состоянием разряжения в спутной струе, а смещённые массы воздуха начинают возвращатся назад под действием давления окружающей атмосферы. При этом разряжение над крылом резко встречается с зоной избыточного давления под крылом. На границе напряжённого объёма в конусе Маха и релаксантного участка в спутной струе возникает узкая граница резкого изменения плотности воздуха от избыточного давления к разряжению (и на оборот с другой стороны крыла). Именно эта линейная граница разных плотностей воздуха ярко проявляется на снимках в шлирен-освещении резкой оптической неоднородностью. При этом сама по себе тёмная линия на шлирен-изображении не даёт возможности понять разряжение в ней или сжатие, или это граница различных плотностей воздуха по разные стороны от неё. (см.рис. 36-37)

Рис. 36. Фото оптических неоднородностей, вызванных пролётом пули на разных скоростях. Левая- 700-800м/с, средняя- около 400м/с, правая- менее 330м/с (нет ударного фрона на острие, то есть уже дозвуковой полёт). О скорости пули свидетельствуют угол отклонения тонкой линии ударной волны от острия пули.

Рис. 37. Фото оптических неоднородностей (ударных фронтов), вызванных пролётом пули на скорости около 700-800м/с.
Последний снимок (рис.37) особенно интересен появлением заметного ударного фронта от тонкой кольцевой канавки в задней половине пули. То есть локальное незначительное изменение на практически параллельной к скорости поверхности пули вызывает появление выраженного ударного фронта, простирающемся на значительное удаление в пространстве и времени.
Фактически данный поясок создаёт маленькое высокочастотное шумовое включение в основное низкочастотное возмущение от пролёта пули. Тем самым эта фотография подтверждает и так известный из «Акустики» факт, что слышимые нами звуки формируются последовтельностью чередований фронтов плотности воздуха различной величиной давления в них и с различной шириной (длиной волны). Последовательно пущенные волны так и следуют друг за другом без смешивания, неся информацию о колебательных характеристиках источника звуковой волны.
Также на снимке (рис.37) интересно то, что сход потока с донного среза пули вообще не вызывает никакого заметного глазом оптического следа, а ударная волна присоединения возникает много дальше за концом пули на удалённом участке сжимающейся спутной струи.
То есть при мягком по кривезне сходе потока с твёрдого тела на спутный след возможна ситуация, когда спутный след становится как бы нейтральным продолжением твёрдого тела (т.н.«фиктивное тело»).
А возникающие линии ударных волн при соприкасновении потоков позади тела обозначают границу этого «фиктивного тела», тогда как в учебниках эти линии расширения-сжатия рисуют строго на задней кромке крыла в случае изображения сверхзвукового полёты крыла.
Монин Илья Алексеевич, к.т.н.МГТУ им.Баумана., imoninpgd@gmail.com
Прошёл ещё год с момента публикации последних частей этой статьи (сейчас 10 июля 2021).
В итоге за два с половиной года с февраля 2019 года статья набрала более 64 тыс. просмотров (из них 23 тыс. просмотров за последние полтора года), что показывает неослабевающий интерес людей к этой достаточно плохо объяснённой в физике теме.
Желающих поделится впечатлениями или замечаниями прошу обращаться по электронной почте: imoninpgd@gmail.com
Ответов на сайте ХАБР давать не могу, так как лишён возможности отвечать из- за глубоких минус 50 в карме.
Зачем продолжать изучение аэродинамики крыла, если самолёты и так прекрасно летают?
При создании каждой новой версии для привычных и общеизвестных теорий нужно ответить на один важный вопрос: Что нового может дать эта новая версия теории?
Для модели явления «подъёмной силы крыла» за счёт отклонения потока воздуха таким новым качеством является теоретический расчёт подъёмной силы для крыльев в виде тонких радиусно изогнутых пластин, для которых привычная теория по Бернулли не давала вразумительного ответа.
Интересным выводом из новой модели является то, что возможен прямой переход от теоретического расчёта к эмпирической формуле, получаемой экспериментально.
На сегодня при продувке макета крыла в АДТ экспериментально получают значение
Fкр=V^2* q*S*Cy/2
Где V- cкорость горизонтального полёта крыла сквозь воздушное пространство, q- плотность воздуха, Су- экспериментальны коэффициент для расчёта вертикальной составляющее от силы сопротивления потоку воздуха.
При этом крайне важно наличие множителя «2» в знаменателе, так как её вносят просто как множитель в величине скоростного напора Pv= V^2*q/2
При этом конкретное Cy и Cx для конкретного крыла на конкретном режиме продувки вбирают в себя все неучтённые нюансы аэродинамики обтекания конкретного крыла потоком воздуха, выдавая в конце вполне закономерный правильный экспериментальный результат.
В случае радиусного тонкого крыла мы можем рассчитать величины Сх и Су прямо из геометрии крыла, после чего сравнить результат и сделать некие интересные и далеко идущие выводы.
Так для радиусно изогнутой пластин можно рассчитать давление на крыло по формуле
Р= V^2* q*dh/R
Где dh- толщина отклоняемого крылом слоя воздуха, R- радиус кривизны отклоняемого слоя воздуха.
Исходя из ранее проведённых расчётов (см. часть 1) известно, что качество крыла Ккр= В/Н, то есть связано только с геометрией изогнутой пластины.
Достроим к изогнутой пластине действующие радиусы кривизны у её концов, в результате чего получаем равнобедренный треугольник ABD с высотой DE. (см.рис.1)
При этом из условия подобия треугольников ABC и ADE можно вычислит значение для радиуса кривизны R.
Так треугольники ABC и ADE подобны по критерию равенства двух углов у основания (один угол <CAB общий для обоих треугольников, а другой угол прямой у каждого треугольника отдельно).

Рис.1. Геометрия треугольника на хорде радиусного крыла для расчёта радиуса кривизны.
При этом, согласно подобию, стороны треугольников соотносятся как
R/(0,5*В)=В/H
Откуда получаем R=0,5*В^2/ Н
Так как в нашей модели радиусного крыла Ккр=Н/В,
То подставляя выражение Ккр в выражение для R получаем:
R=0,5*В^2/ Н= 0,5*В*(В/Н)= 0,5*В *Ккр
Итого: R=0,5*В*Ккр
Теперь полученное выражение для R можно подставить в выражение для давления на крыло, и в результате получаем:
Р= V^2* q*dh/R= V^2* q*dh/ (0,5*В*Ккр)=V^2* q*dh*2/ (В*Ккр)
Итого: Р= V^2* q*dh*2/ (В*Ккр)
Мы получили формулу связи давления на крыло с шириной крыла В (легко замеряемой линейкой) и безразмерным коэффициентом Ккр (однозначно получаемым для профиля при продувках в АДТ).
Теперь для получения величины подъёмной силы Fкр на крыле нам достаточно площадь крыла Sкр=B*L умножить на величину давления на крыло Р, и получаем:
Fкр=Sкр*Р= B*L* V^2* q*dh*2/ (В*Ккр)
Сокращаем однородные члены «В» в числителе и знаменателе и получаем:
Fкр= L* V^2* q*dh*2/ Ккр
Формула совершенно нетривиальная, так как оказалось, что подъёмная сила крыла с известным качеством Ккр зависит только от длины крыла L и зоны влияния по толщине поджимаемого слоя dh, но не зависит от ширины крыла В.
При этом в числителе появился множитель «2», а вовсе не в знаменателе, как это принято писать в выражении скоростного напора.
Теперь приравняем традиционное выражение подъёмной силы крыла с экспериментальным коэффициентом «Cу» к выведенном нами выражению для тонкой радиусной пластины:
Fкр=V^2* q*S*Cy/2
Fкр= L* V^2* q*dh*2/ Ккр
Приравняв правые стороны двух выражений, получаем:
V^2* q*S*Cy/2= L* V^2* q*dh*2/ Ккр
Сокращаем однородные члены:
S*Cy/2= L* dh*2/ Ккр
Раскладываем площадь S прямоугольного в плане крыла как S=B*L и подставляем в выражение:
B*L *Cy/2= L*dh*2/ Ккр
Снова сокращаем однородные члены и получаем:
B*Cy/2= dh*2/ Ккр
В этом выражении неизвестен только один параметр, а именно зона влияния dh. Вот его мы и выразим:
dh= (B*Cy/2)/ (2/ Ккр)= (B*Cy/2)*(Ккр/2)= B*Cy*Ккр/4
Итого: dh= B*Cy*Ккр/4
Данное выражение удивительным образом позволяет определить расчётом условную зону деформированного слоя воздуха вокруг крыла из его собственной геометрии и вполне легко замеряемых в АДТ силовых параметров на крыле.
Можем рассмотреть значение параметра «dh» на параметрах от продувки эталонных профилей в АДТ.

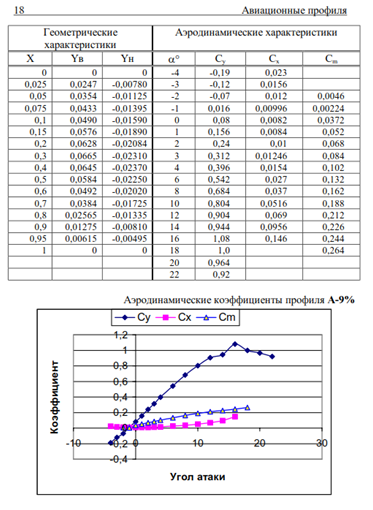
Рис.2. Профиль А-9% из справочника и его характеристики Су и Сх с продувки в АДТ.

Рис.3. Профиль А-18% из справочника и его характеристики Су и Сх с продувки в АДТ.
Рассмотрим профиль А-18% и сравним с А-9%
Для толстого профиля на углах 4 градуса Ккр=18 при этом Су=0,486, что даёт нам расчётный dh=В*0,486*18/4=2,187*В.
Для угла 18 градусов Ккр=7,47 при этом Су=1,23, что даёт нам расчётный dh=В*1,23*7,47 /4=2,3*В
На промежуточных углах атаки 8-12 градусов величина влияния возрастает до более чем dh=3*В. (см.таб.рис.4)

Рис. 4. Таблица экспериментальных и производных аэродинамических характеристик профиля типа А с относительной толщиной 18%.
Таким образом, как для режима полёта с наибольшим качеством крыла (крейсерская скорость), так и для посадочного режима (минимальный Ккр при максимальном Су) зона влияния «dh» имеет толщину более двух хорд крыла.
Это расчёт достаточно ярко показывает, что нужно делать для реализации бипланной схемы самолёта с максимальной эффективностью.
При этом мы брали толстый профиль с относительной толщиной 18%, более характерный для тихоходной авиации первой трети 20-го века.
Если взять профиль для более скоростных самолётов с относительной толщиной 9%, то принципиально картина не изменится.
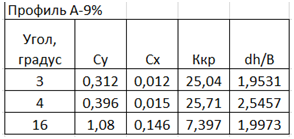
Рис. 5 Выборочная таблица аэродинамических характеристик профиля типа А-9%.
Для угла 4 градуса Ккр=25,7 при этом Су=0,396, что даёт нам расчётный dh=В*0,486*18/4=2,545*В.
Для угла 16 градуса Ккр=7,39 при этом Су=1,08, что даёт нам расчётный dh=В*1,08*7,39 /4=1,997*В
Таким образом, из всего сказанного можно сделать вывод, что для создания эффективного биплана нужно делать большое расстояние между крыльями, а именно более 2,5 хорд крыла. Только при этом взаимном положении взаимное влияние крыльев в полёте будет минимизировано.
В противном случае, при более близком положении ярусов крыльев, взаимное влияние значительно снизит общую подъёмную силу системы крыльев.
Из этого заключения можно сделать интересный вывод про эффективность аэродинамической схемы самолёта-биплана АН-2.
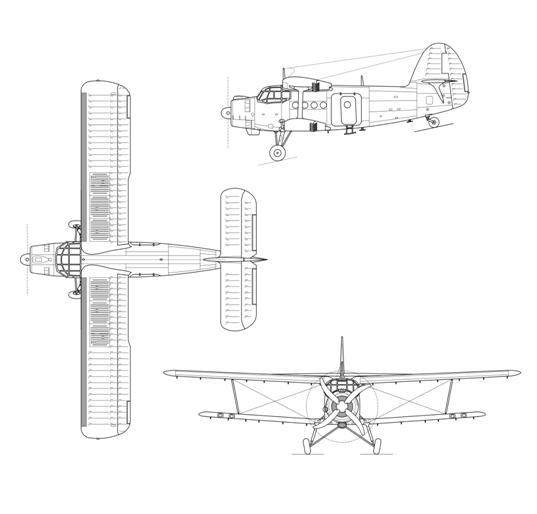
Рис.6. Вид биплана Ан-2, чертёж в трёх проекциях.
Так хорошо видно, что расстояние между ярусами крыльев заметно меньше хорды крыла. То есть у биплана Ан-2 присутствует сильное взаимное влияние параллельно расположенных крыльев, чем резко уменьшается их суммарная подъёмная сила.
Из экспериментальных исследований в АДТ известно, что для биплана Ан-2 прибавка подъёмной силы составляет всего около +20%, чем если бы самолёт имел только одно монопланное верхнее крыло того же размера (то есть при почти в два раза меньшей площади крыльев).
По сути, самолёт сделан бипланом только ради создания крупноформатной несущей фермы, где высота фермы почти равна хорде крыла. При этом горизонтальные балки из двух рядов крыльев распирались одной жёсткой и прочной распорной стойкой между крыльями, а также стягивались тонкими диагональными растяжками из стальных тросов.
Такое решение позволяло сделать более прочное и относительно лёгкое крыло для тяжёлого самолёта из не очень прочных и не самых лёгких материалов, доступных для гражданской авиации на момент создания АН-2.Таким образом, выигрыш по массе и стоимости самолёта был достигнут в ущерб максимальной скорости и топливной экономичности полёта.

Рис.7. Поляра самолёт Ан-2 в целом на различных режимах выпущенной механизации крыла.

Рис.8. Табличная форма для поляр самолёт Ан-2 в целом на различных режимах полёта с гладким крылом и выпущенной механизацией крыла с расчётом дополнительных параметров. Цветом выделены предельные режимы полёта (крейсерский и посадочный режим).
Максимальное качество самолёта Ан-2 в целом находится в районе К=11,2 на крейсерской скорости, а в посадочном режиме около К=4,5.
При этом на больших углах атаки Ан-2 показывает К=4,5 как на гладком крыле, так и с с выпущенной механизацией крыла (предкрылки + закрылки).
Вот только с выпущенной механизацией возникает совершенно запредельны Су=1,966, позволяющий садится на скорости 91км/ч с полной массой 5500кг. (см. рис.7-8.таб.)
И этот коэффициент отнесён к суммарной площади двух крыльев, что при их неравномерной загрузке обеспечивает для отдельных частей крыльев Су = 3...4
Такой удивительно большой Су=2 требует какого-то объяснения, так как ближайший по характеристикам толстый профиль из справочника не даёт столь высокого показателя при достаточно вменяемом Ксам=4,5.
Ниже приведён профиль с максимальным Су из справочника.

Рис.9. Профиль Р-III (15,5%) из справочника и его характеристики Су и Сх с продувки в АДТ.
Профиль вообще выглядит малообтекаемым, с крутолобым передним краем и максимум толщины на 0,2 хорды.
При этом профиль имеет достаточно высокий К=17,5 на угле атаки 4 град, при одновременно высоком Су=0,56.
Так что не случайно данный профиль был применён на множестве различных планеров в 1930-х годах в СССР.
Кстати, и у Ан-2 профиль крыла очень похож на Р-III (15,5%), (см. фото. рис.10).
И совсем похожим на Р-III (15,5%) профиль крыла у Ан-2 становится при сдвинутом вперёд и вниз предкрылком. (см. рис.11).

Рис.10. Профиль крыла самолёта Ан-2 в реальном срезе (фото).

Рис.11. Профиль крыла самолёта Ан-2 в чертеже.
Современные прототипы для замены АН-2 делаются уже по монопланной схеме (самолёты: «Байкал» — ЛМС-901, «Грач» Т-101).(см.рис.12-13)
Так сейчас прочность современных композиционных материалов уже позволяет обеспечить нужную прочность крыла при допустимом его весе в чистом монопланном исполнении (или только с дополнительными подкосами, без полноценного толстого нижнего крыла).
То есть по сути нижнее крыло для АН-2 требовалось только как прочная балка пространственной фермы, а в аэродинамическом качестве оно больше мешало, чем помогало.

Рис.12. Экспериментальный ремоторизованный моноплан «Грач» Т-101 на базе планера АН-2, построен на Московском авиационном производственном объединении (МАПО) в конце 1993г.

Рис. 13. Перспективный композитный самолёт «Байкал» — ЛМС-901
В итоге монопланный «Байкал» — ЛМС-901, как заместитель для АН-2, оказывается по всем лётными качествами значительно лучшими самолётом, чем старик Ан-2.

Рис.14. Таблица сравнения характеристик самолёта Ан-2 и его современных «заместителей».
Так ЛМС-901 оказался в полтора раза быстрее на крейсерской скорости, чем АН-2.
При этом ЛМС-901, при большей грузоподъёмности и большей дальности полёта, имеет почти на 1500 кг меньший сухой вес при меньшем размахе крыльев и в два раза меньшей площади крыла, чем у АН-2.
И только по посадочной скорости моноплан проигрывает биплану, что как раз и связано с аномально высоким Су крыльевой системы биплана.
Учитывая полученные новые знания об аэродинамике во взаимном влиянии крыльев в бипланной схеме, можно предложить схему биплана, который в размерности и габаритах АН-2 будет летать быстрее и экономичнее.
Для этого достаточно разнести крылья на большую высоту друг от друга и укоротить их по длине в полтора раза. Правда, самолёт такой конфигурации больше напоминает воздушный змей, чем нормальный привычный самолёт.
Суммарная длина двух крыльев эффективного биплана будет составлять 120% от длины одного верхнего крыла АН-2. (см.рис. 15 )
Также можно попытаться создать триплан с более узкими крыльями (см.рис. 16 ).
Уменьшение хорды в 2 раза снижает удельную грузоподъёмность крыла (на погонный метр) в те же два раза, так что триплан с зауженным крылом придётся строить с размахом крыла почти как у АН-2, что нецелесообразно.
Рис.15. Эквивалентная АН-2 конструкция биплана с разнесением крыльев за пределы их зон аэродинамического взаимного влияния.

Рис. 16. Схема триплана на базе Ан-2 с зауженными в два раза крыльями для снижения высоты зон аэродинамического влияния и уменьшения расстояния между крыльями.
В начале 1920-х были популярны полипланные схемы, что отразилось в появлении натурных образцов и трипланов. Но из-за непонимания сути явления «подъёмной силы крыла» и недоучёта взаимного влияния крыльев триплан показал крайнюю неэффективность даже в сравнении с бипланом. Пример такого самолёта является КОМТА, созданный под непосредственным руководством Н.Е.Жуковского, профессора в области аэродинамики.

Рис. 17. Чертёж в трёх проекциях триплана КОМТА образца 1923г. (автор Жуковский Н.Е.)
Если бы Жуковский просто приказал выломать среднее крыло из конструкции своего триплана, оставив его силовой каркас, то самолёт сразу полетел бы гораздо лучше. Но «мэтр» жил в своём иллюзорном мире заблуждений об аэродинамике, и такая яркая неудача в прикладном конструировании самолёта не смогла его ничему научить.
Тем не менее, не смотря на общий негативный результат применения полипланной схемы в конструировании самолётов, был один удивительный пример аж семиплана с 7-ю параллельными рядами узких крыльев с большим расстоянием между ними (см.рис.18-19). Появился он в США в 1923 году, тогда же когда и неудачный триплан Жуковского в России. Его построил американский инженер Фредерик Герхардт (W. FrederickGerhardt), сотрудник Мичиганского университета.
Этот самолёт-семиплан умудрился взлететь даже на мускульной тяге, то есть двигателем был сам человек, крутивший велосипедные педали внутри корпуса!!!
И хотя полёт был всего на несколько метров в длину и на 0,6 метра ввысоту, но сам отрыв от земли этого типа ультралёгких самолётов является большим успехом.
До попытки самостоятельного взлёта на педалях данный семиплан уже вполне успешно взлетал на буксире за автомобилем (как воздушный змей), после чего автор решился на самостоятельны взлёт. Но вот недостаток мощности человеческих ног автор семиплана недооценил.
С тех пор мало кто возвращался к полипланной схеме в мускулолётах, хотя именно в этом классе мультплан имеет значительный преимущества в сравнении с монопланом с единым толстым крылом.
При наличии современных прочных материалов вполне можно повторить рекордный семиплан на новом качественном уровне, уже понимая суть проблемы полипланных крыльев. Хотя на воздушных привязных змеях, дельтапланах, парапланах и парашютах люди и так уже давно летают, что по сути очень близко к данному мультиплану.

Рис. 18. Фото семиплана-мускулолёта образца 1923г. (автор Фредерик Герхардт (W. FrederickGerhardt), сотрудник Мичиганского университета.)

Рис.19. Фото семиплана-мускулолёта образца 1923г. за мгновение до взлёта и крушения. Крылья хилой конструкции сложились при попытке взлёта сразу после отрыва самолёта от земли, не выдержав значительной нагрузки от подъёмной силы крыльев.
В современном мире полипланные крылья используются в ограниченной области ультра-высоких сверхзвуковых скоростей в качестве аэродинамических рулей ( сверхзвуковые ракеты и баллистические сверхзвуковые снаряды). При этом полипланные рули выглядит как решётка с квадратными ячейками, а ширина планок решётки равна размеру ячейки в плане. (см.фото. рис.20-26)

Рис.20. Фото решётчатых аэродинамических рулей (полипланных) у ракеты на подвеске крыла боевого самолёта.

Рис.21. Фото решётчатых аэродинамических рулей у разгонного блока боевой ракеты.

Рис.22. Фото решётчатых аэродинамических рулей у гражданской ракеты-носителя Фалькон 9 (США).

Рис.23. Фото решётчатых аэродинамических рулей у гражданской ракеты-носителя СОЮЗ (Россия).

Рис.24. Фото в цеху: на стенде решётчатый аэродинамический руль от гражданской ракеты-носителя Фалькон 9 (США).

Рис.25. Фото решётчатых аэродинамических рулей на гражданской ракете-носителе Фалькон 9 (США) в сравнении с людьми.
При продувке такого аэродинамического полипланного решетчатого крыла в АДТ на дозвуковой скорости был получен весьма низкий Ккр=2,5, что объясняется значительным взаимным влиянием близко расположенных параллельных крыльев и большим паразитным сопротивлением перпендикулярных распорок с частым шагом. Но на кратных сверхзвуковых скоростях у такого решётчатого руля недостатки обращаются в достоинства, так как взаимное влияние плоскостей в решётке резко снижается. Так зона влияния крыльев на сверхзвуке рассчитывается уже по углу конуса Маха, что означает ширину влияния в каждую сторону не больше ширины хорды крыла деленной на число Маха М:
Сверхзвуковой dh= B/M
К полипланным схемам крыла также можно отнести современный планирующий парашют типа «летающее крыло», только с нулевым расстоянием между крыльями (нет щели сзади между плоскостями). Кстати у парашюта-крыла тоже низкое качество крыла Ккр=2,5, то есть такое же, как и у решетчатых рулей.
Низкое качество крыла тряпочных крыльев-змеев не позволяет применять их для мускулолётов.
Так энергетическая оценка «тягового двигателя» для парашюта при Ккр=2,5 даёт мощность около 5 кВт: для парашютиста с парашютом общей массой 100кг и вертикально скоростью снижения Vверт=5м/с (приемлемая посадочная вертикальная скорость) мощность тяги от сил тяжести по вертикали (она же и для для горизонтального полёта при пассивном планировании) составит около N=100кг*9,81*5= 5кВт, что никак не вписывается в возможности мускулолётов.
При поступательной скорости Vгор=Ккр*Vверт=2,5*5= 12,5м/с (45км/ч) полёт и приземление без защитной кабины и колёсного шасси становится уже достаточно опасным действием, а потому без манёвра резкого торможения перед посадкой парашютисты не приземляются.
У парашюта-крыла есть верхняя плоскость, нижняя плоскость и зазор между ними с вертикальными стойками-мембранами.
По фотографии парашюта в полёте видно, что давление внутри купола выше атмосферного, что видно по выпуклой форме натянутой ткани, как на верхней, так и на нижней поверхности купола. Общая выпуклость парашюта-крыла говорит, что давление внутри купола выше, чем избыточное давления от набегающего снизу потока воздуха.
Таким образом, при известной массе человка с парашютом и известной площадью купола можно оценить создаваемые куполом удельные Су и Сх при планирующем полёте. При площади спортивного купола-крыла 12м.кв и массе человека с амуницией 80кг получаем нагрузку около Fy=7кг/м.кв (70Па).
Скоростной напор по горизонтали на скорости 45км/ч (12,5м/с) составит:
Рv= (12,5)^2*1,2/2=94Па
Тогда для крыла получим параметр Су:
Су = Fy/Pv =70/94= 0,74
Что при К кр=2,5 даёт Сх= Cy/Ккр = 0,74/2,5 = 0,3
Однозначно можно сказать, что купол парашюта-крыла надут избыточным давлением равным скоростному напору от поступательной скорости его полёта. То есть внутри купола воздух почти не движется или движется много медленнее, чем скорость полёта (небольшой расход воздуха вбок за счёт просачивания сквозь ткань), ведь у современных куполов вообще нет выходных отверстий на задней кромке крыла. (см.рис.26-27)
У круглых парашютов типа Д6 с площадью купола 80м.кв при массе человека с амуницией 140кг получаем нагрузку около Fy=140/80=1,75кг/м.кв (17,5Па).
При этом при скоростью спуска 5м/с скоростной напор:
Рv=5^2*1,2/2=15Па
В итоге можем получить коэффициент лобового сопротивления тела сложной формы ( чаши купола кромками на поток с щелями по бокам) (см.фото.рис.28), что даёт нам Сd круглого парашюта:
Сd = Fy/Pv =17,5/15= 1,17
Такой Сd прекрасно соответствует справочным значениям для тел вращения (см.главу 2-3)

Рис.26. Фото парашюта типа «Крыло», вид спереди на воздухозаборы купола.

Рис.27. Фото парашюта типа «Крыло», вид сзади на отсутствие выхода воздуха сзади купола.

Рис.28. Фото круглого десантного парашюта, с щелями в куполе для создания горизонтального ускорения полёта.
Куда же девается воздух с пути купола парашюта, который не смог протиснутся сквозь протоки купола?
Почти весь воздух отклоняется от летящего купола, воспринимая его как единое твёрдое тело. Таким образом, купол крыла можно рассматривать как твёрдое крыло гигантского размера, летящего по воздуху с балансировкой и управлением за счёт изменения положения подвешенного снизу крыла груза (парашютиста). Аналогичную гравитационную балансировку применяют на дельтапланах (см.рис.29) и на сверхлёгком сверхвысотном беспилотном самолёте NASA Helios.(cм.рис.30)

Рис.29. Фото дельтаплана. Управление углом атаки и креном крыла дельтаплана осуществляется отклонением центра масс подвешенного пилота по отношению к крылу.

Рис.30. Фото сверхлёгкого сверхвысотного беспилотного самолёте NASA Helios, ширина крыла более 2,5м., размах крыла более 70м. Управление углом атаки крыла осуществляется отклонением центра масс подвешенных снизу крыла опор шасси по отношению к крылу.
Похожее явление запирания потока воздуха (как у купола парашюта-крыла) происходит между крыльями биплана.
Так сильно опущенный вниз закрылок верхнего крыла заужает проход для воздуха, таким образом, верхнее крыло как бы утолщается на величину отгиба закрылка. (см.рис.31)
То есть отклоняя закрылок верхнего крыла удаётся преобразовать аэродинамику верхнего крыла биплана в подобие гигантских толстых крыльев тихоходных самолётов – гигантов конца 1920-х начала 1930-х годов. (см.часть №2 этой статьи)
На малых скоростях полёта бипланов сжатие потока за счёт давления скоростного потока крайне мало и почти не обнаружимо на глаз. Так при взлёт-посадочных скоростях 90км/ч (25м/с) у Ан-2 скоростной напор всего 375 Па, что с учётом базового атмосферного давления 100кПа даст поджатие потока всего на 0, 375% по толщине слоя воздуха (3,75мм на 1 метр слоя).
Поэтому воздух не способен протискиваться в узкие щели на повышенной скорости при столь малых избыточных давлениях, а потому вынужден обходить дальней стороной такие сужающиеся щели между плоскостями.
Невозможность равномерно течь по всей ширине зазора между крыльями вызывает образование застойных зон постоянного давления в неудобных для протекания потока местах.
Критерием «удобного» маршрута прохода потока является соблюдение двух условий:
— максимальная постоянна ширина потока (максимальный расход при постоянной скорости);
— минимальна кривизна потока (максимальный радиус кривизны дуги).
Эти два критерия дают минимальное сопротивление прохождения воздуха через препятствие.
Исходя из этого критерия можно построить приблизительную картину протекания воздуха между крыльями в посадочном режиме на больших углах атаки с выпущенной механизацией крыла.
Распределение давления между крыльями биплана в посадочном режиме с полностью выдвинутой механизацией крыла видно на рисунке, моделирующем протекание воздуха (см.рис.31)
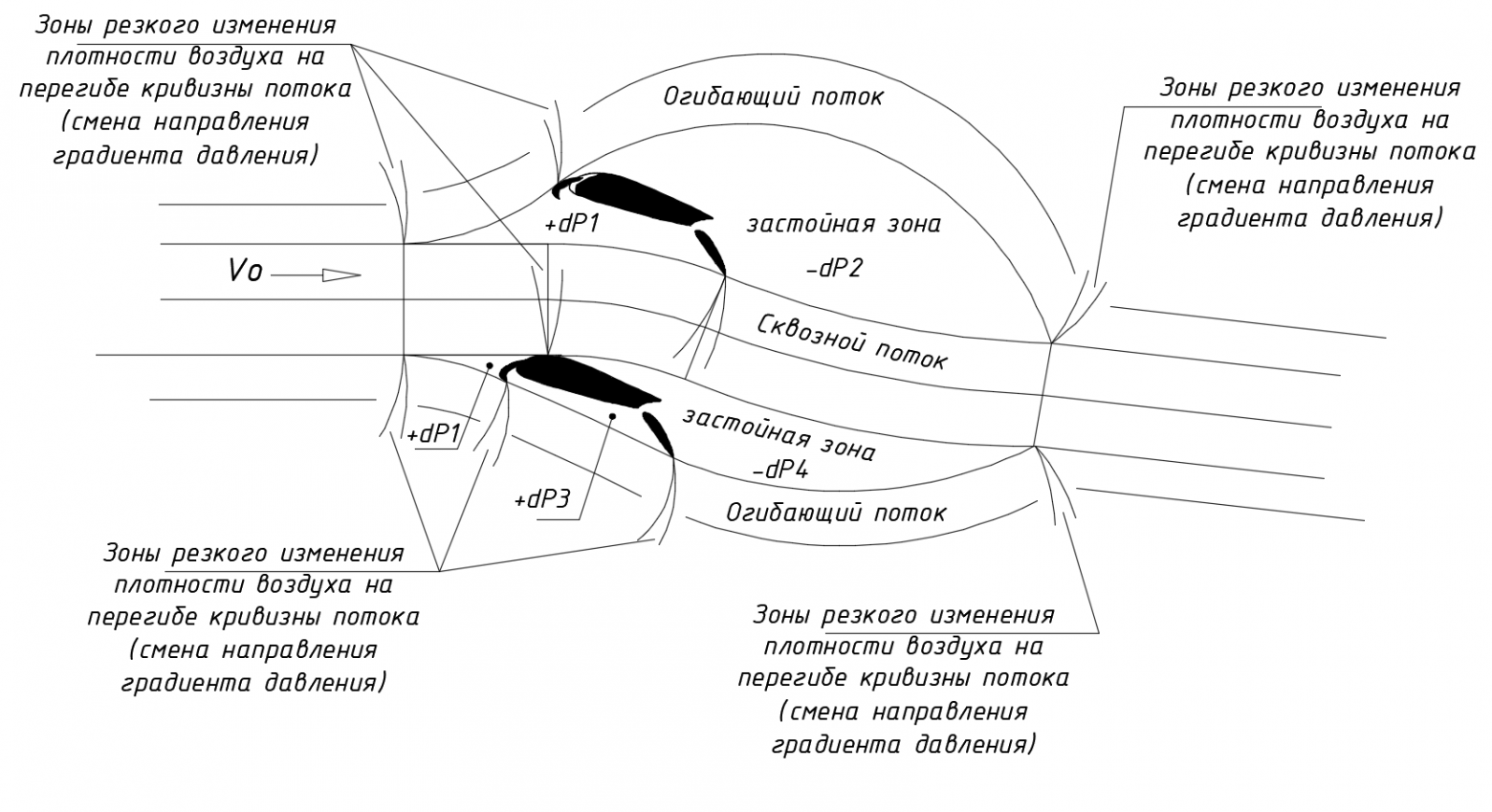
Рис.31. Схема воздушных потоков вокруг крыльев при посадке Ан-2 на углах атаки 16град при полностью выпущенной механизации крыльев (предкрылки + закрылки), и возникающие при этом застойные зоны с постоянным давлением.
В направленных на набегающий поток зонах в лобовой части крыльев возникает давление
dP1= Pvo.
То есть на лобовых обтекателях в застойных зонах давление одинаково и равно скоростному напору от скорости полёта Vo.
Давление в тени крыльев уже связано с режимом обтекания отрывной струи над конкретной застойной зоной.
Малая зона под нижним крылом с dP3 может иметь как положительное, так и отрицательное значение. Также dP3 может быть равным с dP4, если отрывной поток не касается отогнутого вниз закрылка, оставляя всю нижнюю плоскость в объёме большой нижней застойной зоны.
Разрежение dP2 больше (абсолютное давление меньше), чем у dP4, что и объясняет загиб сквозного потока вверх (выпуклость в сторону большего давления, то есть вниз) после выхода из зазора между крыльев.
Из данного распределения давления следует, что нижнее крыло может создавать небольшую отрицательную или положительную подъёмную силу, а верхнее крыло создаёт очень большую положительную подъёмную силу.
Хоть нижнее крыло и может создавать отрицательную подъёмную силу, но без работы нижнего крыла верхнее крыло так сильно бы не нагрузилось, образуя огромные застойные пузыри положительного и отрицательных давлений вокруг себя.
Особого внимания заслуживают веерные линии в зонах смены плотности воздуха (изменение градиента давления) при резком (ударном) изменении направления потока воздуха. При этом скорость воздуха практически постоянна по модулю (долями процента на сжатие-расширение потока пренебрегаем).
Данные зоны смены градиентов давления на шлирен-фотографиях видны как тёмные полоски. В традиционном объяснении Подъёмной силы крыла по Бернули эти веерные тёмные полосы объясняют ударными волнами на границах перехода на сверхзвуковое течении воздуха над крылом, что неверно (воздух там никуда бешенно не разгоняется, тем более до сверхзвука).
Вообще расчёт самолёта достаточно простая штука, а наличие абстрагированных безразмерных показателей Ккр, Су и Сх позволяет легко просчитывать общие показатели будущих самолётов практически на салфетке за несколько минут.
Расчёт № 1.
Попытаемся просчитать конструкцию и аэродинамику мускулолёта.
Главным ограничивающим фактором в конструкции мускулолёта является мускульная мощность человека, которую можно принять на уровне Nдв=250Вт в длительном режиме.
Это реалистичная оценка дана по мощности электровелосипедов, которые на такой мощности длительно едут со скоростью более 20км/ч, что значительно быстрее среднего человека на велосипеде на одних педалях.
Далее мы можем принять некий расчётный вес самого человека и вес конструкции: пусть это будет 75 кг и 75 кг.
Тогда общий взлётный вес составит m=150кг.
Сопротивление полёту зависит только от качества крыла, которое мы примем достаточно высоким на уровне Ккр=20 (сопротивление фюзеляжа пока не учитываем)
Тогда имеем силу сопротивления:
Fх=mg/Ккр=9,81*150/20=75Н
Исходя из располагаемой мощности 250 Вт можно получить доступную скорость взлёта, а именно:
Vвз=N/Fx=250/75=3,33м/с (11,8км/ч)
Зная скорость и характеристики профиля при Ккр=20, можем определить необходимую площадь крыла и соответствующий общий размах крыла.
Так исходя из ранее приведённых аэродинамических характеристик профиля типа А для Ккр=20 коэффициент подъёмной сила составит приблизительно Су=0,45.
При скорости взлёта V= 3,33м/с скоростной напор составит Pv= 3,33^2*1,2/2= 6,65Па
А площадь крыла потребуется S=m*g/(Су*Pv)=150*9,81/(0,45*6,65)=491м.кв.
Для монопланной схемы такое крыло длиной в 200-500м вообще выглядит запредельно длинным, а весь проект неосуществимым.
А вот для полиплана крыло площадью 491 м.кв. превращается в квадратную этажерку с размером
L= ( S*2,5)^0,5=35м
Квадратная конструкция из крыльев с размером 35х35 м уже будет более реалистичной. При этом общий внешний размер квадратной «этажерки» не изменится при выборе широких или узких крыльев в её заполнении.
Хотя я слабо представляю себе из чего сделать крылья общей площадью 491 м.кв + вертикальные стойки схожего погонажа, при этом вписавшись в общий вес менее 75 кг, или около 0,15 кг/м.кв.
При относительной толщине даже 9% крыло из лёгкого пенопласта с плотностью 35кг/м3 уже будет весить около 1,5кг/м.кв. или в 10 раз тяжелее допустимого.
То есть технически практически не достижимы нужные для мускулолёта массо-габаритные характеристики его несущих конструкций.
Так даже обтяжка профиля с двух сторон плёночным лавсаном (плёнка липкой ленты) с плотностью 1400кг/м3 и толщиной всего 0,1мм, даёт уже около 0,28кг/м2 площади крыла.
А ведь ещё и прочный каркас будет что-то весить!
То есть полиплан-мускулолёт должен трансформироваться в подобие воздушного змея из тонюсеньких плёночек толщиной менее 0,05мм из прочнейших полимеров и тонкого каркаса из углепластика. Воздушного змея подобной полипланно-плёночной конструкции можно посмотреть на фото (см.фото.рис.32).

Рис.32. Воздушный змей полипланно- плёночной конструкции(крыло нулевой толщины).
Расчёт № 2.
Проведём альтернативный расчёт, изменив качество крыла в сторону уменьшения, но при этом подняв Су профиля.
Так тот же профиль типа А-18% при качестве крыла Ккр=12,5 обеспечивает Су=1,06.
Повторяем расчёт при новых характеристиках.
Fх=mg/Ккр=9,81*150/12,5=117,7Н
Тогда доступная скорость составит
Vвз=N/Fx=250/117,7=2,12м/с (7,6км/ч)
При скорости взлёта Vвз= 2,12м/с скоростной напор составит Pv= 2,12^2*1,2/2= 2,69Па
А потребная площадь крыла будет:
S=m*g/ (Су*Pv)=150*9,81/ (1,06*2,69)=516м.кв.
То есть удивительным образом цифра общей площади крыла практически не изменилась при одинаковой мощности двигателя, но при разном качестве крыла.
Вывод :
Результаты двух расчётов однозначно показывают, что мускулолёты являются практически нереализуемыми конструкциями по массо-габаритным параметрам.
Но современные строители мускулолётов стараются выйти из этого конструктивного тупика, поднимая мощность на двигателе, то есть сажая в мускулолёт опытных и тренированных мужчин-велосипедистов, способных в течении длительного времени выдавать на педалях мощность до 1 кВт.
Для сравнения 1 кВт – это подъём со скоростью 1м/с по вертикали груза 100кг. То есть нужно иметь способность забежать по лестнице быстрее лифта (скорость лифта в 9-этажках равна 1м/с) с грузом на плечах (суммарно 100 кг массы от своего веса и груза на плечах). В юности я мог обогнать лифт бегом на 9-й этаж, но с 30 кг на плечах этого я бы уже не смог исполнить даже тогда.
В итоге на скоростях 7-8 м/с (25-28 км/ч) и с мощностью 1 кВт мускулолёт уменьшается по массе до 40-50кг и при размахе крыльев около 30м.
То есть если общий взлётный вес 120кг при качестве крыла Ккр=12, то сопротивление составляет Fу= 100Н, что на скорости 7м/с (25км/ч) требует мощности более 900Вт ( 700 Вт сопротивление крыла + потери в цепной передаче передаче и на КПД винта), скоростной напор Рv= 7^2*1,2/2=29Па позволяет лететь на крыле площадью 35-45м.кв при Су=1, 08 (характеристика планерного крыла P-III (15,5%) на угле атаке 12град, см. рис.9)
Мировой рекорд дальности для мускулолёта — это перелёт на расстояние 115 км за 3 часа 54 минуты 59 секунд (средняя скорость 29,36 км/ч) по маршруту с острова Крит на материк, который совершил греческий велосипедист-спортсмен K. Канеллопулос ( выступал за Грецию на летних Олимпийских играх 1984) на мускулолёте «MIT Daedalus » 23 апреля 1988 года. Аппарат имел размах крыльев 34,75 м, а площадь крыла составила 35,0 м².(см.рис.33)
При площади крыла всего 35м.кв и массе СЛА в 45 кг на 1 квадратный метр крыла приходится уже почти 1кг материала, то есть реально уже обтянуть профиль крыла двумя слоями лавсана по 0,05мм и останется ещё 800грамм на 1 м главного лонжерона (улепластиковая тонкостенная труба большого диаметра) и нервюру профиля из упрочнённого тонкослойного пенопласта.

Рис.33-а. Вид рекордного мускулолёта Дедал образца 1987года на испытаниях в пустыне Калифорнии.

Рис.33-б. Вид рекордного мускулолёта Дедал, который в 1988г совершил рекордный перелёт с о.Кипр на материк на дистанцию 115км.
Расчёт № 3.
Зато, если мы поднимем мощность двигателя всего до 3 кВт с собственным весом двигателя всего около 6 кг (мощность и вес двухтактной бензопилы), то наш летательный аппарат резко уменьшится
Так тот же профиль типа А-18% при качестве крыла Ккр=12,5 обеспечивает Су=1,06.
Повторяем расчёт при новых характеристиках.
Fх=mg/Ккр=9,81*150/12,5=117,7Н
Тогда доступная скорость составит
Vвз=N/Fx=3000/117,7=25,4м/с (или 91км/ч, как и у Ан-2)
При скорости взлёта Vвз= 25м/с скоростной напор составит Pv= 25^2*1,2/2= 375Па
При этом потребная площадь крыла будет:
S=m*g/ (Су*Pv)=150*9,81/ (1,06*375)=3,7м.кв
То есть даже с малюсеньким бензиновым двигателем в 3 кВт можно взлететь на самолётике с двумя маленькими крыльями, каждое размером как обычная межкомнатная дверь!
Расчёт № 4.
Если же поднять мощность авиационного двигателя всего до 20 кВт и увеличить взлётную массу самолёта до 300кг (200кг на саму конструкцию + 100кг на вес человека и топлива), то такой самолёт приобретёт вполне привычный вид лёгкого спортивного самолёта.
Так тот же профиль типа А-18% при качестве крыла Ккр=20 обеспечивает Су=0,45.
Повторяем расчёт при новых характеристиках.
Fх=mg/Ккр=9,81*300/20=150Н
Тогда доступная скорость составит
Vвз=N/Fx=20000/150=133м/с (или 480км/ч)
При скорости полёта V= 133 м/с скоростной напор составит Pv= 133^2*1,2/2= 10600Па
А потребная площадь крыла будет:
S=m*g/ (Су*Pv)=300*9,81/ (0,45*10600)=0,62м.кв
То есть два крыла, каждое размером всего 1,0х0,31м, на скорости 480км/могут удержать самолёт в полёте.
Видели малюсенькие крылышки у крылатых ракет, более похожих на торпеды с большими плавниками? (см.рис.34)
Так вот это реальные размеры «крыльев-плавников», которые вполне легко получаются простым расчётом!

Рис.34-а. Крылатая ракета с маленькими прямоугольными крыльями ( макет, вид сверху).

Рис.34-б. Крылатая ракета с маленькими прямоугольными крыльями (натуральный вид на выставочной площадке).
Расчёт № 5
От высокой скорости полёта можно перейти к меньшим скоростям на больших углах атаки.
Так тот же профиль типа А-18% при качестве крыла Ккр=9,4 обеспечивает Су=1,2
Повторяем расчёт при новых характеристиках.
Fх=mg/Ккр=9,81*300/9,4=313Н
Тогда доступная скорость составит
Vвз=N/Fx=20000/313=64м/с (или 230км/ч)
При скорости взлёта Vвз= 64 м/с скоростной напор составит Pv= 64^2*1,2/2= 2457Па
А потребная площадь крыла будет:
S=m*g/ (Су*Pv)=300*9,81/ (1,2*2457)=0,998м.кв
То есть два крыла, каждое размером всего 1,0х0,5м, на скорости 230км/ч могут обеспечить взлёт самолёта и удержать самолёт в полёте.
Такими характеристиками обладают современные лёгкие спортивные самолёты, только садятся и взлетают они на сильно меньших скоростях на больших УА при отклонённых вниз закрылках. Пример: Сверхлёгкий самолёт Colomban MC-15 Cri Cri (Cricket) (см.рис.35.а-г.)
Крейсерская скорость полёта 180 км/ч
Скорость сваливания 70 км/ч
Наилучшая скорость набора высоты 160 км/ч
Дистанция на посадке до полной остановки 250 м
Взлётная дистанция 200 м
Страна производитель Россия
Год выпуска 2017
Высота с хвостовой стойкой 1.5 м
Дальность полета с максимальной загрузкой 463 км
Мощность двигателя 30 л. с.
Длина разбега 200 м
Размах крыльев 4.9 м
Максимальный взлетный вес 170 кг
Площадь крыла 3.1 кв.м
Емкость топливных баков 40 л
Максимальная коммерческая загрузка 92 кг
Вес пустого 78 кг
Длина 3.9 м

Рис.35.а. ТТХ сверхлёгкого самолёта Colomban MC-15 Cri Cri (Cricket)

Рис.35.б. Заход на посадку с отклонёнными закрылками сверхлёгкого самолёта Colomban MC-15 Cri Cri (Cricket)

Рис.35.в. Фото на аэродроме сверхлёгкого самолёта Colomban MC-15 Cri Cri (Cricket) рядом с человеком и лёгким самолётом привычного размера для сравнения (вид сбоку).

Рис.35.г. Фото на аэродроме сверхлёгкого самолёта Colomban MC-15 Cri Cri (Cricket) рядом с лёгким самолётом привычного размера для сравнения (вид сзади).
Именно такие простые обосновывающие расчёты и определяли бурное развитие авиации после изобретения и начала массового выпуска достаточно компактных и мощных бензиновых двигателей.
Причём для расчёта не требуется глубокое понимание аэродинамики, а лишь достаточно таблиц коэффициентов Су и Сх от продувок профилей крыла в АДТ, которые проводились повсеместно в 1920-х.
Расчёт № 6
Из спортивного интереса можно провести оценочный расчёт для дальнего межконтинентального бомбардировщика с задачей доставки ядерной бомбы массой 10 тонн на дистанцию 10 тыс.км., после чего сравним результат расчёта с характеристикой реального Ту-95.
Так тот же профиль типа А-9% (см.рис.2. в начале главы) на углах атаки около 4 градусов Су=0,396 и Сх=0,154 обеспечивает качество крыла Ккр=25,7.
Дополнительно учтём сопротивление фюзеляжа, так что общее Ксам=16..18 ( у Ан-2 показатель Ксам=11, у современного А-320 уже Ксам=18, у свободно парящих планеров Кплан=30…50)
Масса самолёта при взлёте принята 180 тонн (80 тонн планер+ 90 топливо + 10 тонн бомба) как у известного нам Ту-95.
Повторяем расчёт при новых характеристиках.
Fх=mg/Ксам=9,81*180 000/16=110 360Н ( или 11 тонн тяги)
Пример крейсерскую скорость V=800км/ч (222м/c) на высоте 10км при плотности воздуха 0,42кг/м3. (см.рис.36)
Тогда мощность тяги составит N= Fx*V= 110 360*222=24 499 920 Вт (или 24,5 МВт или 32 тыс. л.с.)
С учётом КПД винта= 0,9 получим Nном=27МВт
Расход топлива у ДВС составляет 250г/(кВт*ч), таким образом, расход топлива самолёта на крейсерской скорости составит 27*0,25*1000=7500кг/ч
90 тонн запаса топлива обеспечивают 90/7,5=12 часов полёта, а дальность составит 12*800=9600км.
Реальная дальность полёта будет больше, так как с расходом топлива уменьшается масса самолёта и падает потребная мощность двигателя, увеличивая длительность полёта при том же запасе топлива. Так пустой самолёт к концу полёта будет тратить около 4тонн/ч, то есть средний расход составит 6т/ч, длительность полёта поднимется до 15ч, а дальность полёта вырастет до 15*800=12 тыс.км.
Теперь посчитаем площадь крыла.
Так при скорости 222м/с и плотности воздуха 0,42кг/м3 скоростной напор составит:
Pv = 222^2*0,42/2=10350Па
А потребная площадь крыла будет:
S=m*g/ (Су*Pv) =180 000*9,81/ (0,4*10350)=426 м.кв

Рис.36. Таблица давления и плотности воздуха по высоте от поверхности земли.
А теперь посмотрим реальные характеристики Ту-95. (см.рис.37-39)

Рис.37. Таблица характеристик самолёта Ту-95.
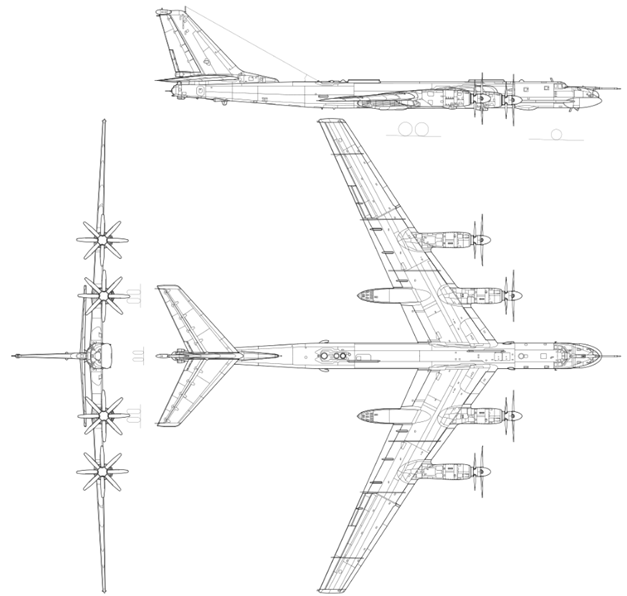
Рис.38. Общий вид самолёта Ту-95 (чертёж в трёх проекциях).
Сразу видно что мы вполне точно посчитали мощность двигателя ( 4х8948=36МВт, что оставляет запас мощности в 35-40% для взлётного режима), а значит при одинаковом запасе топлива в 90 тонн мы приняли правильное аэродинамическое качество Ксам и получили реалистичную дальность полёта.
Видно, что главное отличие наших расчётов от реального самолёта- это площадь крыла всего 289м.кв (против насчитанных нами 426м.кв) при средней нагрузке на крыло 640кг/м.кв (6,5кПа). То есть реальное крыло в 1,47 раза меньше по площади, чем у рассчитанного нами.
Из чего можно сделать вывод, что у реального Ту-95 показатель Су=0,6 при том же Ккр=20..25.
Противоречит ли это нашей нашей теории?
Нет, не противоречит!
В том же справочнике Авиационных профилей мы обнаруживаем профиль ЦАГИ-731 (толщина профиля 10,6%) (см. Таб. рис.39), у которого для угла атаки 6 градусов Су=0,604 при Сх=0,0288, что даёт нам Ккр=21.
На первый взгляд профили вообще не отличимы, но чуть большая толщина и тупоносость у профиля ЦАГИ -731 (10,6%) дают чуть более высокие Су и большую удельную грузоподъёмность при равных Ккр.
Он же для угла атаки 4 градуса Су=0,442 при Сх=0,0194, что даёт нам Ккр=22,8.
Он же для угла атаки 2 градуса Су=0,294 при Сх=0,0120, что даёт нам Ккр=24,5.



Рис.39. Сравнение профилей А-9% и ЦАГИ-731 (10.6%) из справочника и их характеристики Су и Сх с продувки в АДТ, где у профиля ЦАГИ-731 (10.6%) создаются большие Су при меньших УА и более высоких Ккр (большая удельная грузоподъёмность профиля).
То есть на обратном пути с бомбёжки, полегчав на половину запаса топлива и вес бомбы, Ту-95 начинает тратить уже в 1,5 раза меньше горючего в единицу времени. В конце же маршрута перед самым аэродромом с пустыми баками самолёт летит с часовым расходом топлива более чем в 2 раза меньше, чем при вылете с аэродрома на бомбёжку.
Итого:
Простейшим оценочным расчётом на нескольких листах бумаги и с применением простейшего калькулятора (арифмометра) мы добились практически 100% попадания нашего оценочного аэродинамического расчёта в реальные ТТХ реального стратегического бомбардировщика Ту-95. При этом сделали мы этот расчёт с опорой лишь на открытые справочные данные из 1930-х годов о продувках профилей крыла на АДТ, а также применив базу знаний из школьного курса физики раздел «механика».
Вернёмся к удельным массовым показателям конструкции самолёта. Так будем считать, что для Ту-95 доля самого планера без узлов шасси и двигателей составит половину сухого веса, что равно 40 тонн чистого авиационного дюраля с плотностью 2,7г/см3.
Считаем, что общая площадь поверхности крыльев (с двух сторон), фюзеляжа и хвостового оперения составляет около 1000 м2. Тогда на каждый квадратный метр поверхности придётся 40 000/1000= 40 кг алюминия, или лист толщиной 40/2,7=14мм. В итоге из такого количества алюминия мы можем получить однослойную общивку из листа 3-4мм, под которой с шагом в 200 мм будет установлен набор рёбер высотой 200мм с шагом 200мм в двух взаимно перпендикулярных направлениях. Такая ребристо-ячеистая конструкция планера вполне может выдержать распределённую нагрузку в 600кг/м2 в полёте. Примеры ребристого несущего усиления обшивки видны на фото (см.рис.40-43).

Рис.40. Силовой набор фюзеляжа пассажирского самолёта при изготовлении в цеху (полуфабрикат перед сборкой).

Рис.41. Силовой набор фюзеляжа пассажирского самолёта при изготовлении в цеху.

Рис. 42. Силовой набор крыла самолёта: опущенный бесщелевой закрыло-щиток на лёгком самолёте на стоянке в аэропорту.

Рис. 43. Силовой набор крыла большого авиалайнера в цеху.
Так что у огромных Ту-95 и малых лёгких самолётов со слабенькими бензиновыми движками даже в быстрой грубой оценке реалистичность конструкции значительно выше, чем у лёгких мускулолётов.
Часть № 7.
Гидродинамика полёта на подводном крыле на примере СПК " Ракета" Ростислава Алексеева (СССР).
Полёт на крыльях возможен не только в воздушном пространстве, но и в водной среде.
К таким гидролётам относятся глиссирующие суда и суда на подводных крыльях (далее СПК).
Для этих двух типов быстроходных судов общим является гидродинамическое удержание над водой в процессе движения на крейсерской скорости.
В то же время на стоянке или на малых скоростях оба типа судов становятся обычными водоизмещающими судами.
С точки зрения гидро-газодинамики нам интересны больше суда на подводных крыльях, так как они осуществляют чистый полёт на тонких узких крыльях внутри водяного полупространства, а большой корпус с людьми и грузами летит сквозь воздух с малым сопротивлением (малым в сравнении с водоизмещающим режимом на той же скорости).
Для понимания гидродинамики подводного крыла крайне интересны диаграммы, найденные мной в публикации на тему подводных крыльев аж от 1964 года. (см.рис.2.)
Ссылка на источник:
Проектирование и расчет подводных крыльев (Судостроение / Технологии) — Barque.ru
При этом надо представлять что такое сегментный профиль относительной толщиной е=0,06 (или 6% от ширины). (см.рис.1): это узкий сегмент круга с угловой величиной 26 градусов (13*2=26) и углом схода поверхностей на острых кромках 13градусов.
13 градусов – это очень острое лезвие, приблизительно как у кавалерийской сабли.
При заданной ширине крыла 500мм толщина профиля 6% составляет 30мм. Радиус кривизны цилиндрической поверхности крыла составляет R=1056мм.

Рис.1. Вид сегментного профиля крыла СПК при ширине 500мм и относительной толщиной 6%.

Рис.2. Диаграммы характеристик Сх, Су, К сегментного крыла СПК в зависимости от глубины погружения и углов атаки.
Из диаграммы В) видно, что максимальное качество крыла составляет около К=16.
Экстремально высокий К=19 не рассматриваем, так как он относится к глубоко погружённому крылу с глубиной 2В (В- ширина крыла).
При интересующих нас глубинах погружения крыла 0,1-1В показатель Су=0,2-0,3 на углах атаки УА=2-4 градуса с максимально возможным К=16.
При попытке получить больший Су на больших углах атаки резко падает качество крыла К.
Удвоение Су приводит к снижению качества крыла до величины К=11.
Нам известно, что у СКП два основных режима движения:
1.Выход на глиссирование и вставание на крыло на малых скоростях 20 км/ч.
2.Крейсерская скорость 60км/ч на крыльях с полным отрывом корпуса от воды.
То есть на этих двух режимах нам нужно использовать разные кривые с разным соотношением К- Су с диаграммы.
При разгоне СПК на первом режиме наиболее применимы высокие Су=0,5-0,65 при К=11.
На крейсерской скорости нужно учитывать только кривую для малопогруженного крыла с низким Су=0,3 при высоком К=15.
Дополнительно нужно будет учесть сопротивление вертикальных стоек, на которых будет держаться несущее крыло, и сопротивление корпуса воздушному потоку на крейсерской скорости.
Сопротивление для стоек будет на уровне минимального Сх для подводного крыла с нулевым углом атаки.
Что из этого следует?
А следует то, что энергетическая эффективность судов на подводных крыльях оказывается такое же, как и у самолёта АН-2, который имеет качество планера целиком Кп=11 на крейсерской скорости 190км/ч.
То есть экономичнее круглый год летать на АН-2, чем всего полгода эксплуатировать на реках корабли на подводных крыльях.
Для эталонной ракеты со полной массой 24 тонны на крейсерской скорости 60км/ч при Су=0,3 и К=15 крыла нужна площадь подводных крыльев способная удержать СКП как на высоких скоростях, так и на низких стартовых.
Скоростной напор воды на крейсерской скорости 60км/ч составляет:
Р=(60/3,6)^2*1000/2=138900 Па=138,9 кПа или 14157кг/м2
То есть для крейсерского экономичного режима нужна площадь подводных крыльев:
S=24000/(0,3*14000)=5,7м.кв
Что при ширине крыла 500 мм составит длину крыльев почти 12 м.
А вот при выходе на крылья из водоизмещающего режима при скорости около 20км/ч крыльев нужно побольше.
Скоростной напор воды на крейсерской скорости 20км/ч составляет:
Р=(20/3,6)^2*1000/2=15430 Па=15,4кПа или 1572кг/м2
То есть для разгонного режима даже при в два раза большем Су=0,65 нужна площадь подводных крыльев почти в 4 раза больше:
S=24000/(0,65*1572)=23,5м.кв
Что соответствует длине крыла 47м при ширине 500мм.
Судя по фото «Ракеты» снизу (см.рис.3), где видна явная ширина подводного крыла и его можно сравнить с шириной окна в корпусе, при этом ширина окна составляет около 1м.
Получается что переднее крыло СПК имеет по факту ширину около 1,2м.
Тем самым при ширине корпуса в 5 м суммарная площадь двух крыльев превышает 12 м.кв.
То есть с выходом на глиссирование на больших углах атаки корпуса и с помощью дополнительных приспособлений в виде глиссадных лыж ( на фото (см. Рис.4-6) лыжи с брызгоотбойными экранами видны сразу за стойками передних крыльев) разгон и выход полностью на крылья вполне осуществим.

Рис.3. Вид на СПК «Ракета» снизу, где видна реальная ширина подводных крыльев.

Рис. 4.Вид на СПК «Ракета» спереди анфас, где хорошо видна глиссадная лыжа с брызговыми экранами позади передней стойки подводного крыла. На фото хорошо видно, что лыжа перестает касаться уровня воды только при очень малом заглублении подводного крыла.

Рис.5. СПК «Ракета» в стадии разгона, что видно по заметному погружению глиссадной лыжи в воду. Позади переднего подводного крыла под днищем СПК хорошо заметна водяная яма, образованная за счёт отброса воды вниз от подводного крыла.

Рис.6. СПК «Ракета» на полном ходу, что видно по полному поднятию из воды глиссадной лыжи. Позади переднего подводного крыла под днищем СПК хорошо виден бурный кавитационный след, который начинается мелкими пузырьками под водой на середине плоскости переднего подводного крыла( т.е. давление на верхней плоскости подводного крыла упало 0,02 атм, что соответствует кипению воды при +20С)
Исходя из полученных данных можно подобрать двигатель для условной «Ракеты» с полной массой 24 тонны.
На стартовом режиме со скорости 20км/ч при Кп=4 (режим глиссирования с сильно замоченным корпусом) мощность сопротивления составит
N=24000*9,81*20/(3,6*4)=327000Вт= 327кВт
На крейсерской скорости 60км/ч при Кп=15 (оптимистично) мощность сопротивления составит
N=24000*9,81*60/(3,6*15)=261600Вт= 262кВт
На крейсерской скорости 60км/ч нужно добавить лобовое сопротивление, которое для СПК с поперечным сечением около 20м.кв и коэффициентом лобового сопротивления Сд=0,8 (грубая оценка в сравнении с Сд=0,8 как у куба ребром на ветер, а у Шара Сд=0,5) составит:
Fвозд=20* (60/3,6)^2*0,8/2=2222Н или 227кгс
Мощность на воздушное сопротивление потребуется
Nвозд=2222*(60/3,6)=37033Вт=37кВт.
Сопротивление стоек опор крыла в количестве 6шт с высотой под водой 0,3 м, толщиной 40мм и лобовым сопротивлением Сд=0,015/0,06=0,25 составит
Fвод=0,25*6*0,3*0,040* (60/3,6)^2*1000/2=2500Н или 254кгс
Мощность на водяное сопротивление стоек потребуется
Nвозд=2500*(60/3,6)=41666Вт=42кВт.
Получается суммарная мощность сопротивления:
Nr=262+37+42=341кВт
Где 79 из 341 кВт или 23% общей мощности сопротивления движению приходится на сопротивление корпуса в воздухе и стоек опор крыла в воде.
Доля 23% потерь от стоек и корпуса в общих потерях — это означает падение общего гидродинамического качества СПК от К=15 (только для самого крыла) до К=15*(100-23)/100=11,55.
Таким образом СПК «Ракета» точно совпал с самолётом АН-2 по общему аэродинамическому качеству К=11,5
Мощность на разгоне при выходе на крыло(327 кВт) практически совпадает с необходимой мощностью на крейсерской скорости(341 кВт), что означает необходимость постоянной работы двигателя на номинальной мощности как на крейсерской скорости, так и при разгоне.
С учётом КПД винта и валопроводов на уровне n=0,5 для нашего СПК потребуется двигатель
Nдв =341/0,5=682 кВт или 927 л.с.
Для проверки заглядываем в википедию и видим близкую цифру мощности двигателя 900-1000л.с. (в зависимости от модификации) (см.рис.7).
Учитывая некоторые перезаклады по площади лобового сечения корпуса и высоту погружённых стоек на крейсерской скорости, то можно считать, что расчёты практически совпали с реальными ТТХ СПК «Ракета».

Рис.7. ТТХ СПК «Ракета» согласно Википедии.
Столь точное попадание нашего оценочного расчёта по диаграмме К-Су в справочные характеристики реального СПК «Ракета» позволяет сделать вывод о причинах резкого взлёта темы больших СПК в 1960-1970 годах в СССР и быстрый сход темы в 1990-х.
Причина угасания интереса к эксплуатации пассажирских СПК является чрезвычайная энергоёмкость, а потому и дороговизна перевозок, в сравнении с резко прибавившему в массовости шоссейному автотранспорту.
Расход топлива дизельным двигателем оценочно 200г/л.с.*ч
Для СПК с ДВС в 1000л.с. расход топлива составит 200*1000= 200кг/ч. или 235л/ч при плотности солярки 0,85кг/л.
За 1 час СПК преодолеет 60км на крейсерской скорости, при этом расход топлива составит 235л/65чел=3,61л/чел*60км
Аналогичный по вместимости пассажиров рейсовый автобус имеет ту же крейсерскую скорость в 60км/ч, но при этом расход топлива в 13-22 раз меньше в пересчёте на одного пассажира*км.
В такой же пропорции 20:1 соотносятся и стоимости созданных по авиационным технологиям алюминиево-титановых СПК со стоимостью производства обычных железных рейсовых автобусов, что также не добавляет конкурентных качеств для СПК.
Сравним реальные образцы массовых автобусов времён позднего СССР по топливной экономичности на одного пассажира с СПК.
ЛиАЗ-677 имел мощность ДВС 180л.с…
Контрольный расход топлива ЛиАЗ-677 при 40 км/ч — 35,0 литров на 100 км, или 14л/ч, или 21л/60км пробега.
В пересчёте на человека на дистанции 60 км получим показатель 21/80=0,262 л/(чел*60км)
В сравнении с СПК «Ракета» автобус ЛИАЗ-677 экономичнее в 3,61/0,262=13,7 раз
Его современник Икарус-280 (гармошка) был в 2 раза более вместительным (146чел) при этом имел расход всего 40л на 100км/пути при 60км/ч, что в пересчёте на 60км пробега расход составит всего 40*60/100=24л/(60км).
В пересчёте на человека на дистанции 60км получим 24/146=0,164 л/(чел*60км)
В сравнении с СПК «Ракета» автобус Икарус-280 экономичнее в 3,61/0,164=22 раз

Рис. 8. ТТХ городского рейсового автобуса ЛиАЗ-677 согласно Википедии.
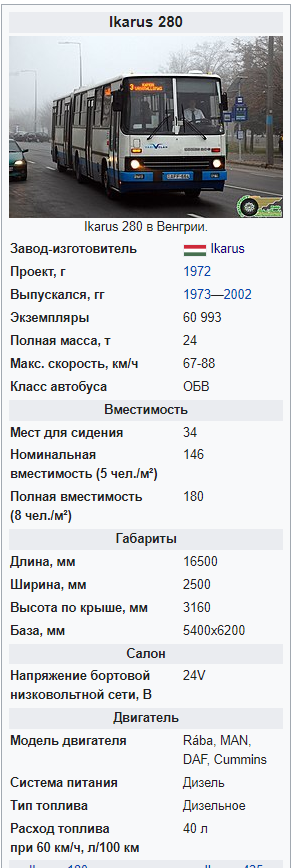
Рис. 9. ТТХ городского рейсового автобуса Икарус-280 (гармошка) согласно Википедии.
По итогу можно сказать, что ЛЕТАТЬ на короткие расстояния — это ДОРОГО.
И не важно где ваши крылья находятся: в воде или в небе, — в итоге вы всё равно проиграете легковому автомобилю или автобусу на дистанции до 500км.
На дистанциях 500-1500 км по экономичности в равных предпочтениях самолёт или поезд.
На расстояние дальше 1500км (сутки на поезде) однозначно уже выгоднее летать дальней авиацией на современных аэробусах.
Правда тут в экономику входят не только топливо, но и расход времени пассажира. Так большинство людей не готовы ехать целую неделю в поезде из Москвы до Владивостока, если туда же можно долететь всего за сутки, даже с учётом доезда поездом или автобусом до не самого ближнего аэропорта, с учётом прибытия за 3 часа до рейса и 9 часов самого чистого полёта.
Аналогичную с СПК судьбу имела малая региональная авиация на самолётах типа АН-2: она вымерла в конкурентной борьбе с автобусами и расплодившимися личными автомобилями, которые оказались на много удобнее в пользовании на резко улучшившихся асфальтовых дорогах.
Но даже в эпоху СССР речные СПК не могли заменить регулярное пригородное сообщение по суше, так как на зиму навигация останавливалась. В результате СПК стали дотируемым государством транспортным аттракционом, которым пользовались житель приречных городов.
Чаще всего СПК возили дачников по выходным дням на отдалённые 6-соточные участки, отрезанные от города рекой и не имеющие близкого по расстоянию альтернативного автомобильно-автобусного маршрута.
Но что у конкурентов на Западе?
В условиях глобального противостояния сверхдержав США не могли не ответить технологическому вызовы от СССР. В результате в 1974 году на свет появился американский СПК от авиационной компании Боинг.

Рис.10. ТТХ СПК Боинг -929 согласно Википедии.
СПК Боинг 929 должен был во всех показателях опережать «этих советских», и это Боингу удалось (см.рис.6)
-Он был быстрее«Ракеты» (80км/ч против 70 км/ч у ),
— он был в 4 раза тяжелей «Ракеты» (104 т против 25 тонн)
— он брал на борт в 5,4 раза больше пассажиров (350 чел против 65 чел)
— он имел два двигателя (газотурбинные авиационные двигатели) по 3400кВт каждый или около 6800 кВт (9250л.с) в пиковом режиме суммарно, что в 9 раз больше, чем один двигатель «Ракеты».
— он потреблял в 9 раз больше топлива в час (2150л/ч против 235л/ч)
Особенно мне нравится последний пункт про гигантский часовой расход топлива, но корректнее будет пересчитать на одного пассажира на стандартном для нашего сравнения 60км маршруте.
Так на одного пассажира СПК Боинг 929 потратит Мт=2150*60/(80*350)=4,6 л/(чел* 60км)
То есть по итогу Боинг 929 проиграл «Ракете» по топливной экономичности в
4,6/3,61=1,27 раза.
С учётом конструктивных особенностей двигателя и движителя Боинга 929 такая разница вполне закономерна.
В качестве двигателей американцы применили авиационные турбины вместо судовых дизелей. Турбины очень лёгкие и мощные в сравнении с дизельными двигателями, но очень прожорливы на неноминальных режимах, что снижает общую топливную экономичность судна на коротких маршрутах, где доля времени на маневрирование в водоизмещем режиме достаточно велика.
В качестве движителя был использован водомёт, что также понизило итоговый КПД системы.
В целом данные решения закономерны, так как американские конструкторы СПК сразу начали проектировать «Водяной самолёт», а не корабль (см.Рис.10. — название типа: «самолёт на подводных крыльях»).
В технических решениях это оказался именно «самолёт» с богатой механизацией крыла.
Так у Боинга 929 были установлены закрылки, облегчающих «взлёт» из воды на малых скоростях. (см рис.12,13,14)
Были у Боинга и подводные элероны, позволяющих совершать маневры по-самолётном, закладывая на высокой скорости вираж с креном внутрь круга.(см рис.17).
При этом на советских СПК подводные крылья механизацией не оснащали.
Советские СПК в повороте имели сильный крен наружу из поворота (как у обычных водоизмещающих кораблей и автомобилей). Для удержание от опрокидывания в поворотах с креном судна наружу использовали принципы остойчивости по-корабельному, то есть восстанавливающий момент против крена наружу из поворота создавался гидродинамическим усилением подъёмной силы наружной части крыла при большем его заглублении в воду при крене.
Не смотря на своё техническое совершенств более технически сложный и дорогой СПК Боинг 929 в итоге разделил судьбу более простых и более экономичных СПК из СССР.
Низкая топливная экономичность даже для американцев стала убийственным фактором в судьбе СПК Боинг.
После нескольких лет эксплуатации в 1970-80х годах СПК Боинг 929 ушли со сцены.
В наше время в тёплых островных государствах без долгих морозных зим (Греция, Индонезия) тема быстроходных пассажирских СПК иногда периодически всплывает вновь, но при этом не выходит за рамки туристических аттракционов для «пляжных туристов».

Рис.11. Фото СПК Боинг -929 на полном ходу. Хорошо видна мощная струя воды из водомёта на корме выше уровня воды.

Рис.12. Схема крыльев и силовой установки СПК Боинг -929. На схеме показаны подводный водозабор на средней стойке заднего крыла, маршрут движения воды к водомётам, и управляемы закрылки на подводных крыльях.

Рис.13. Схема крыльев и силовой установки СПК Боинг -929 в сопряжении с корпусом судна. На схеме показаны подводный водозабор на средней стойке заднего крыла, маршрут движения воды к водомётам, и управляемы закрылки на подводных крыльях. Рулевым пером является поворотна стойка переднего подводного крыла (угол поворота+-5,5 град).

Рис.14. Общий вид СПК Боинг -929 с указанием уровня воды на крейсерской скорости.Хорошо видно, что американцы использовали глубоко погруженные подводные крылья с высоким Су, в отличии от мелкопогружённых крыльев СПК авторства Ростислава Алексеева и других СПК из СССР.

Рис.15. Фото переднего подводного крыла СПК Боинг 929 в поднятом из воды положении. Хорошо видны регулируемы закрылки на подводном крыле.
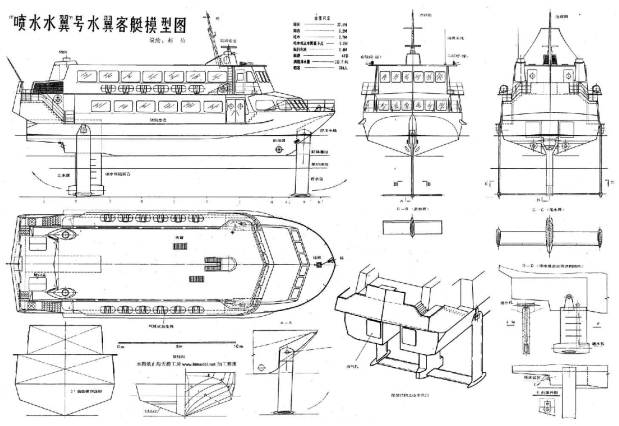
Рис.16. Чертёж в разных видах СПК Боинг -929. На виде на корму хорошо видны отверстия водомётов в корпусе, и их положение относительно уровня воды в водоизмещающем режиме и в полёте на крыле. Также можно замерить относительную глубину погружения крыла составляющую приблизительно 1,5В.
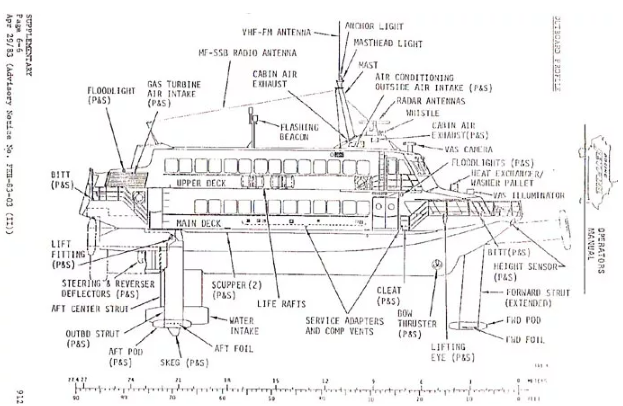
Рис.17. Чертёж вида сбоку СПК Боинг -929. На виде обозначены основные элементы СПК.

Рис.18. Фото СПК Боинг -929 на полном ходу в момент поворота. Хорошо виден крен судна в сторону центра поворота, что означает маневрирование с виражами по-самолётному. то есть преднамеренным созданием крена в повороте с помощью разнонаправленного движения закрылков. В то же время СПК Алексеева (с малозаглублённым крылом без управляемых закрылков) в повороте имели крен наружу из круга циркуляции, то есть компенсация центростремительного ускорения осуществлялось средствами гидродинамической остойчивости «по-судостроительному».
Библиография:
Критика существующего Теоретического объяснения Подъёмной Силы на крыле самолёта
Прослушав курс лекций МФТИ Факультет аэромеханики и летательной техники (ФАЛТ) «Введение в Аэродинамику» и прочитав несколько разных ВУЗовских учеников по «Аэродинамике» [1-3], я был озадачен рядом явных противоречий в объяснениях физики процесса обтекания потоком воздуха (газа или идеальной жидкости) различных твёрдых предметов и формирования подъёмной силы на крыле.
- Основной тиражируемой Версией образования подъёмной силы на крыле заявляется разность скоростей течения воздуха (жидкости) над крылом и под крылом, и вследствие этого возникает перепад давления согласно Закону Бернулли. При этом однозначно связывают через закон Бернулли расчётную скорость потока на поверхности крыла с инструментально регистрируемым давлением на крыло, игнорируя другие возможные объяснения на основе не менее базовых законов физики.
- При анализе обтекания идеальной невязкой жидкостью профилей в плоских течениях удивительным образом получали кратное повышение скоростей потока в сравнение с базовой скоростью V0. То есть опровергается закон сохранения энергии, так как энергия на разгон потока берётся ниоткуда, кратно превышая энергию набегающего на крыло потока. При этом игнорируется постулат гидродинамики, что по тому же закону Бернулли при истечении струи из-под уровня скоростной напор однозначно ограничивается сверху статическим напором в сосуде, то есть скоростной напор струи после разгона на крыле не может превысить статического давление сжатой при торможении среды.
Для полёта современного самолёта необходимая подъёмная сила в 500-600кг/м.кв. При совершении взлёта-посадки скорости современных самолётов составляют около 250км/ч. В этом случае нужная подъёмная сила на крыле обеспечивается при скорости обтекания верхней плоскости порядка 450км/ч.
Каков механизм такого разгона потока воздуха без видимого механизма разгонного воздействия на него?
Ведь контакт крыла с набегающим потоком может вести только к торможению потока, но никак не к его разгону!
Эти противоречия необходимо снять!
Физика не должна терять Физический смысл в угоду красивым и сложным математическим построениям!
Рассмотрим иное объяснение формирования подъёмной силы крыла без выявленных нарушений законов физики и здравого смысла. Для этого потребуются применение законов обычной механики.
В рассмотрении считаем, что воздух состоит из отдельных взаимно отталкивающихся (для создания давления газа) частиц с собственной массой, каждая из которых подчиняется законам механики при изменении её направления и величины скорости движения.
Неоднозначность связи разрежения над крылом с повышенной скоростью потока
Рассматриваемое реальное крыло не является элементом идеальной трубки в модели Закона Бернулли, а является ограниченным твёрдым объектом в неограниченном пространстве движущегося реального газа, состоящего из вполне осязаемых по массе и размеру частиц газа. В таком случае следует рассмотреть криволинейное течение струй над криволинейной поверхностью крыла с учётом сил инерции и создаваемого давления, перпендикулярного вектору скорости и поверхности крыла.
Если рассматривать движение струй над профилем крыла, то создать разряжение над крылом может струя воздуха за счёт криволинейности своего течения.
Так для искривления прямолинейного движения тела нужно приложить силу, в перпендикулярном к вектору скорости направлении. В случае непрерывной плоской струи для её искривления нужно обеспечить разность давлений над и под ней. При этом со стороны выпуклости струи будет повышенное давлении, а с вогнутой стороны- пониженное давление.
При движении по окружности материальной точки центростремительное ускорение будет создаваться силой
F=m*V^2/R
А при таком же круговом движении тонкого слоя газа толщиной dR масса будет равна
m= q*S*dR,
где S- площадь участка слоя газа, q- плотность газа. Если привести центростремительную силу к элементарной площадке слоя газа, сила превратится в давление
P=q*V^2*dR/R
При протекании воздушной струи по поверхности крыла слой газа движется по криволинейной траектории. В каждой точке этой траектории существует свой радиус кривизны, который позволяет посчитать ИНЕРЦИОННОЕ давление газа в перпендикулярном к скорости направлении.
Таким образом, можно напрямую посчитать давление (разряжение) на крыле от слоя текущего над его поверхностью газа, при этом скорость течения газа будем всегда считать равной скорости полёта крыла Vo.
Для начала рассмотрим простейший случай крыла в виде изогнутой с радиусом R пластиной нулевой толщины. Такие тонкие изогнутые профили используют для сверхлёгких планеров в авиамоделизме.
Кстати, по привычной теории с законом Бернулли у тонкой изогнутой пластины вообще не должно быть подъёмной силы, так как длина пути под крылом и над крылом одинакова. Но подъёмная сила у тонкого крыла есть, причём весьма значительная, что однозначно показывает неправильность модели подъёмной силы с применением закона Бернулли.
Для оценочного расчёта крыла выберем привычную для малоскоростных самолётов высоту профиля 20% от ширины крыла. В данном случае за высоту профиля примем разницу высот передней и задней кромки по отношению к горизонтальному воздушному потоку (см.рис.1-3)

Рис.1. Геометрия тонкого крыла постоянной кривизны

Рис.2. Предполагаемый режим обтекания тонкого радиусного крыла

Рис.3. Характер распределения давления по тонкому радиусному крылу и равнодействующие силы по направлениям
Тогда при ширине 1м и 20% высоте профиля радиус крыла составит 2,6м, при условии горизонтального расположения касательной к крылу в верхней точке профиля.
Теперь рассчитаем центростремительное давление на крыло от искривлённого по дуге слоя воздуха.
Так для скорости 70м/с (252км/ч) давление одного слоя толщиной 0,1м с радиусом кривизны 2,6м составляет 235,6Па или 24кг/м.кв., а величина скоростного напора при 70м/с равна 3063 Па.
Если учесть, что у тонкого крыла обтекание происходит с двух сторон, то эти величины нужно как минимум удвоить, а затем ещё и умножить на некоторое количество параллельных слоёв, так же искривлённых двигающимся крылом. Если предполагаем, что толщина возмущённого слоя не менее половины ширины крыла с каждой стороны крыла, то получаем суммарную удесятерённую нагрузку на крыло около 2356 Па. Эти цифры прекрасно бьются со значениями нагрузок на крыло для низкоскоростных лёгкомоторных самолётов с толстым крылом и аналогичной кривизной поверхности крыла. (см.таб.1)
Так как давление Ркр приложено к криволинейной поверхности тонкой пластины, то сила Fкр от Ркр может быть разложена на Подъёмную силы Fy и на силу Сопротивления полёту Fх.
Подъёмная сила Fy равна интегралу проекции на ось Y сил от Давления Криволинейного потока Ркр по всей площади крыла.
В случае равномерного давления на круговое крыло величина Fy будет равна произведению Ркр на площадь проекции крыла на ось Х, что равно S=B*L крыла ( в данном случае 1м.кв/м.п.).
Fy=Ркр*Bкр= 2356*1=2356 Н/м.п.
В то же время сопротивление горизонтальному движению в этом случае будет равно интегралу проекции dFкр на ось Х по всей площади крыла. В случае равномерного давления на крыло величина Fx будет равна произведению Ркр на площадь проекции крыла на ось Y, что равно высоте Н профиля крыла ( в данном случае 0,2м.кв/м.п.).
Fx=Ркр*Нкр= 2356*0,2=462 Н/м.п.
При этом получим К= Fy/ Fx= (Ркр*Bкр)/ ( Ркр*Нкр ) = Bкр/ Нкр, то есть при равномерном давлении на круговом тонком профиле качество крыла равно отношению только геометрических параметров профиля К=В/Н.
В общем виде величина К=В/Н=R*sinAк / (R*(1-cosAк))=sinAк/ (1-cosAк)
(см.график под Таб.4)
Согласно правилу векторного разложения сил из заданной картинки можно сразу получить величину качества крыла К=Fy/Fx, что в данном случае равно К=100*Ркр/20*Ркр =5.
Интересно, что если отмасштабировать данное расчётное крыло в сторону десятикратного уменьшения (по радиусу кривизны, высоте и ширине профиля), то давления на крыло при этом останутся неизменными при равных скоростях полёта (см.таб.2). Именно по этой причине тяжёлые крылатые ракеты летят на достаточно маленьких тонких крылышках. Оказывается, что их небольших по площади и тонких крыльев при достаточной кривизне действительно хватает для создания необходимой подъёмной силы!
Так как комнатный моделизм достаточно дёшев, то эти цифры достаточно просто проверяются на натурных моделях.
Таб.1. Давления искривлённых слоёв воздуха на крыло постоянного радиуса R=2,6 м в зависимости от скорости полёта.

Таб.2. Давления искривлённых слоёв воздуха на крыло постоянного радиуса R=0,26 м в зависимости от скорости полёта.

Интересно рассмотреть, как меняется Ккр крыла при постоянной его кривизне Rкр, но при изменяющемся параметре ширины профиля Вкр. (См.таб.3)
В самой первой строчке таблицы аэродинамическое качество крыла достигает фантастического значения К=182, но при этом нагрузка на крыло составляет всего 67Па (7кгс/м.кв), что пригодно только для авиамоделей планеров комнатной размерности.
Необходимая подъёмная сила на крыле возникает только при достаточно малых К крыла, что видно по последним строчкам таблицы.
Жёлтым выделены столбец изменяемого параметра и строчка исходного профиля с Ккр=5.
Таб.3. Изменение параметров крыла постоянного радиуса R=2,6м при различных углах профиля (ширина профиля) на постоянной скорости полёта.

Также можно рассчитать изменение подъёмной силы Fy и качества крыла Ккр для крыла с постоянной хордой, но разной кривизной крыла при постоянной скорости. Жёлтым выделены столбцы: Изменяемый аргумент Rкр- радиус кривизны и постоянная ширина профиля Вкр. Так же выделена строчка исходного профиля с Ккр=5.
Таб.4. Изменение параметров крыла переменного радиуса кривизны при постоянной ширине профиля В=1м на постоянной скорости полёта. Ниже график качество крыла К (синим, значения по оси Y) и график Fу ( красным, в безразмерном масштабе) в зависимости от угла Ак кривизны профиля крыла по оси Х.


Граф. Зависимость качества крыла (синим) и подёмной силы (красным) от угла профиля Ак по оси X. По оси Y отложены величины качества крыла в безразмерных единицах. Размерность подёмной силы по оси Y условно не показана.
В описанной модели для получения разряжения над крылом не требуется дополнительный разгон воздуха над крылом. Заметное разряжение над крылом обеспечивается в условиях значительного искривления обтекающего крыло потока воздуха под действием статических сил давления воздуха всего окружающего пространства. Угол наклона хорды исходной изогнутой пластины составляет 11,3 градуса (половина угла сегмента дуги в 22,6град), что хорошо согласуется с посадочными режимами работы крыла современных авиалайнеров при посадке с выпущенной механизацией крыла (предкрылки +закрылки). В посадочном режиме крыло с выпущенной механизацией намного больше напоминает рассмотренный случай изогнутой тонкой пластинки, чем классическое крыло с прямой нижней плоскостью (см.рис 4).

Рис.4. Крыло несимметричного профиля с плоской нижней обтекаемой поверхностью: а) выпрямленное положение для скоростного полёта; б) крыло с максимальной кривизной при полностью выпущенной механизацией.
Сильно изогнутое тонкое крыло широко применяется в качестве лопастей вентиляторов. Низкие линейные скорости при малых величинах давления позволяют использовать в вентиляторах в качестве лопастей тонкие стальные или пластиковые пластины крайне малой толщины, так как их прочности хватает для выдерживания имеющихся нагрузок.
У тяжёлых самолётов использование тонких крыльев технически невозможно по причине их недостаточной прочности. Большая толщина крыла позволяет разместить внутри крыла достаточно высокие несущие балки достаточной прочности и жёсткости на изгиб и кручение, при этом сохранив приемлемый для самолёта вес. Именно по этой причине вся аэродинамика изучает крылья со вполне осязаемой толщиной. По этой причине переходим от рассмотрения аэродинамики тонкой изогнутой пластины к профилю крыла с реальной толщиной и плоскостями различной кривизны.
В завершении рассмотрения модели обтекания тонкого крыла необходимо привести ещё одно доказательство работоспособности предложенной модели объяснения «Подъёмной силы крыла». Как известно из механики, Сила- это изменение импульса в единицу времени, то есть
F=d (m*V)/dT
В озвученной модели обтекания тонкого криволинейного крыла мы можем подсчитать подъёмную силу Fy как изменение импульса набегающего потока воздуха по вертикали, который считается как
Fy2= (dR*10*q*Vo)*Vo*sinАкр,
Где Vo-скорость крыла, dR –толщина элементарного искривляемого слоя потока воздуха в расчётной модели, 10- число искривляемых одновременно слоёв, Акр- угол схода потока с крыла к направлению исходной скорости Vo.
Проведя расчёт получим, что оба расчёта дают одинаковый результат.
Или в аналитическом виде:
Fy1=Ркр*Bкр,
Ркр= (dR*10*q*Vo)* Vo/R,
Bкр=R* sinАкр
Подставив развёртки Ркр и Bкр в выражение для Fy1 и сократив одноимённые R в числителе и знаменателе, получим:
Fy= Ркр*Bкр= (dR*10*q*Vo)*Vo*sinАкр
А значит всегда верно равенство Fy =Fy1= Fy2
То есть «Инерционно-криволинейный» метод расчёта «Подъёмной Силы» крыла даёт формулу идентичную с методом «Реактивно-Импульсной Силы» для крыла одинаковой геометрии.
Это значит, что самолёты летают не благодаря какой-то «магической» силе из «магических вихрей», а благодаря старому и понятному «Импульсу Силы» или «Реактивной тяге» при отбрасывании массы воздуха вниз.
Толстое Крыло
На малых скоростях полёта при взлёте-посадке (М= 0,2 или 250км/ч) скоростной напор не превышает 3кПа (3% от Атмосферного давления на уровне моря в 100кПа), то есть он столь мал по отношению к базовому атмосферному давлению, что геометрическое сжатие потока становится визуально не обнаружимо при рисовании струйного течения у крыла.
Для создания подъёмной силы над крылом необходимо создать искривление потока так, чтобы крыло находилось в зоне вогнутости потока воздуха. Обеспечить такое искривление струи над крылом помогает кривизна верхней плоскости крыла, находящейся в аэродинамической тени носового обтекателя крыла.
При этом нижняя плоскость крыла обтекается либо по прямой, не создавая разряжения, или по вогнутой поверхности, отбрасывая поток воздуха вниз, что создаёт уже положительный прирост давления на крыле снизу и суммируется с подъёмной силой от разряжения над крылом.
Главным отличием толстого крыла от тонкой пластины в нашем случае будет появление лобового обтекателя, раздвигающего встречный поток воздуха до того, как он достигнет изогнутых плоскостей, создающих подъёмную силу.
Перед летящим толстым крылом возникает зона торможения, где скорость движения воздуха становится равной нулю (относительно крыла), а избыточное давление в этой зоне равно скоростному напору Рvo.
Нарисовать линии тока без учёта сжатия воздуха не получится, иначе придется либо принять версию об ускорении воздуха над поверхностью крыла, либо зона влияния с искривлением потока устремится к бесконечности в несжимаемой среде, что является неправдоподобным.
Кстати, оба эффекта (Ускорение потока и Бесконечная зона влияния в несжимаемых жидкостях) проявляются на практике в аэродинамических трубах с дымовыми линиями тока и при движении подводных лодок на малых глубинах.
Так в аэродинамических трубах (АДТ) обтекание тестируемых макетов происходит с заметным ускорением потока (уменьшение толщин дымовых линий ) в зазоре стенка АДТ-макет. Вот только толкование этого явления совершенно неверно относят к ускорению потока для формирования подъёмной силы. В действительности ускорение потока в зазоре «стенка АДТ-макет» является просто следствием заужения проходного сечения в проточном тракте АДТ при сохранении постоянного расхода воздуха в самой АДТ за счёт мощных вентиляторов с жёсткой вентиляторной характеристикой.
При движении подводных лодок на малых глубинах над подводной лодкой образуется Визуально Заметный водяной горб. Величина этого горба равна объёму воды перед корпусом подлодки, который надо как-то переместить из зоны перед подлодкой в зону кормы при движении с заданной скоростью. Горб на поверхности образуется и при движении подлодки на больших глубинах, но из-за большей площади растекания горба его высота становится необнаружимой при простом визуальном наблюдении. Причиной возникновения горба воды на поверхности объясняется невозможностью переместить несжимаемую жидкость в сторону дна, а в сторону поверхности тонкий слой воды под атмосферным давлением воздуха становится Легко Сдвигаемым, с понятной упругой характеристикой пружины Атмосферного давления и Сил Тяготения. Кстати, даже при движении подводных лодок на больших глубинах водяной горб (и саму подлодку как следствие) могут обнаружить при наблюдении со спутников с помощью высокочувствительной аппаратуры, способной замерять геометрию поверхности морей с большой точностью и вычленить горб воды от подлодки из шума волн на поверхности с помощью ЭВМ.
Таким образом, принимаем газ сжимаемым, а зону влияния от огибания крыла ставим в зависимость от величины сжатия струи от давления Рvo.
Давление в зоне торможения у обтекателя удерживается искривлёнными струями воздуха, огибающими обтекатель. Связь давления с искривлением слоёв воздуха такая же, как и в случае с тонким изогнутым крылом dP=q*Vo^2*dR/Rсл.
Величина зоны влияния, где заметно искривление потока, также связано с величиной Вкр и Нкр. Повышение давления перед обтекателем будет скомпенсировано понижением давления в спутной струе позади крыла, то есть крыло формирует линейный Диполь по давлению, который на большом удалении практически перестаёт влиять на окружающее воздушное пространство на малых (дозвуковых) скоростях полёта.
Если принять форму носового обтекателя круглой, то половина высоты профиля будет равна Нкр/2=Rлоб.
Считаем, что зона торможения с давлением Рvo целиком создаётся кривизной слоя в границах ширины профиля Вкр, тогда можем оценить радиус кривизны струи толщиной Нкр/2= Rлоб.
Необходимо выполнить условие Pr= Рvo.
Следовательно
qVo^2*Rлоб/R= qVo^2/2
После сокращения одинаковых членов плотности и скорости соответственно в левой и правой части уравнения получаем
R= 2* Rлоб
Таким образом, получается, что предельные радиусы кривизны набегающего потока ограничены исключительно кривизной обтекателя (локальной высотой профиля), и при этом не зависят от скорости.
При повороте набегающей струи в обход профиля неизбежно возникает ситуация, в которой граничная с нулевой линей потока струя касается обтекателя. В этой точке касания скорость потока направляется от крыла, а кривая потока достигает точки перегиба. То есть в этой точке происходит отрыв слоя от крыла с изменением направления выпуклости кривизны струи (см.рис.5).

Рис.5. Взаимодействие набегающего потока Vo с лобовым обтекателем крыла.
На больших скоростях полёта величина скоростного напора Pvo столь велика, что струя отрывается от носового обтекателя и, описав длинную дугу над плоскостью крыла, возвращается обратно к поверхности крыла.
В месте возврата оторванной струи на плоскость крыла возникает Удар, а струя скачком меняет направление на касательное к плоскости крыла. При этом под дугой летящей струи от точки отрыва до точки возврата возникает замкнутая полость низкого давления. (см.рис.6).
В традиционной «Бернуллиевской Аэродинамике» описанное образование развитого отрывного пузыря с сильным разряжением и ударный возврат отрывной струи объясняют так: « …На высоких предзвуковых и трансзвуковых скоростях возникает ускорение потока воздуха над крылом до сверхзвуковых значений, в результате чего давление над крылом сильно снижается, а потом возникает скачёк давления (удар перехода на сверхзвук), с переходом после него на дозвуковое течение…». Такое объяснение выглядит как явная натяжка реальных экспериментальных данных на несостоятельную теорию.
Так как обтекатель делит набегающий поток на две части по нулевой линии, то отрыв потока возникает на обеих плоскостях крыла. Но из-за различных направлений плоскостей по отношению к потоку (на поток или в аэродинамической тени) отрывные пузыри разряжения над и под крылом имеют разный размер, и так же изменяется сила удара возвратной струи, пропорционально размеру отрывного пузыря.
На основе такого распределения эпюр давления на переднем обтекателе крыла и полученых качеств Ккр тонких радиусных пластин-крыльев в зависимости от относительной толщины профиля Вкр./Нкр. легко можно понять причины и закономерности такого явления, как «Обтекаемость» различных геометрических форм (см.Эпюру Сх на рис.6).
Так же было бы крайне интересно рассмотреть эпюры давления при Обтекании струйными течениями стандартных осесимметричных тел и получить их равёртки Сх и Су по сечениям, а не только один суммарный коэффициент Сх для фигуры в целом.

Рис.6. Обтекание струями воздуха толстого крыла с обозначенными характерными элементами движения. Эпюра давлений на крыло и диаграммы коэффициента давления Су по хорде крыла и Сх по высоте крыла. Площадь закрашенных зон соответствуют суммарным силам по направлениям Y и Х соответственно.
При низких числах М основная подъёмная сила формируется в зоне носового обтекателя в отрывных пузырях. При малых числах М возвратная струя в зоне отрыва идёт по касательной к толстому профилю крыла и не вызывает Удара в точке возврата. Но при приближении к М=1 отрывные пузыри раздуваются на столько сильно, что становится невозможно добиться нужной толщины профиля для безотрывного течения струи, и тогда возникает выраженный Отрыв потока с образованием Отрывного Пузыря, визуально наблюдаемого по колебаниям шелковинок, наклеенных на плоскость крыла. Раздувание отрывных пузырей по высоте становится препятствием для набора скорости, и потому их развитие начинают уменьшать за счёт заострения носовой кромки (понижение радиуса лобового обтекателя).
При трансзвуковых скоростях полёта задняя граница отрывного пузыря достигает задней кромки крыла, после чего происходит соединение объёмов верхнего отрывного пузыря с зоной высокого давления нижней плоскости крыла. В объединившихся объёмах верхнего и нижнего отрывных пузырей давление выравнивается, а подъёмная сила крыла Fy резко падает.
При сверхзвуковом полёте крыло привычной каплевидной формы становится уже совсем неприменимым, а вместо этого появляется крыло с развитым острым «клювом», на котором теперь и создаётся основная часть подъёмной силы, при этом минимизируется возможность возникновения отрывного пузыря.
Для обеспечения посадочных режимов полёта на низких числах Маха в «тонкоклювое» крыло осуществляют установку передней и задней отклоняемой механизации (см.рис.7). Подобного типа тонкие крылья с острыми передними кромками и отклоняемой передней и задней механизацией ставят на боевые истребители 4-5 поколений (см.фото.1-2). При отклонения механизации вниз «тонкоклювое» крыло становится близко к характеристикам обтекания тонкой изогнутой пластины, что позволяет осуществлять взлёт и посадку на малых скоростях и с коротким пробегом по ВПП. В перспективе возможен переход на поворот плоскости крыла целиком при выполнении манёвров на малых скоростях, как это уже сделано с полностью поворотным хвостовым оперением истребителей. Полностью поворотная плоскость крыла позволит избегать сильного задирания фюзеляжа против потока воздуха и сохранения сонаправленности вектора тяги двигателей к скорости полёта на больших углах атаки.

Рис.7. Профиль тонкого крыла Н/В=0,1 (10%) с острым отклоняемым «Клювом» и широким отклоняемым закрылком: а) выпрямленное положение для сверхзвукового полёта; б) отклонение механизации вниз для полётов на малых скоростях и в посадочном режиме с большими углами атаки.

Фото.1. Су- 35 на большом угле атаки с отклонёнными предкрылками и закрылками в посадочном режиме (выпущены шасси).

Фото.2. МиГ-29 с отклонёнными предкрылками и закрылками во взлёт-посадочном режиме на большом угле атаки и низкой скорости (выпущены шасси).

Фото.3. МиГ-29 на взлёте с полным отклонением вниз передней и задней механизации крыла.
На фото (см.фото.3) хорошо видна форма «остроклювого» предкрылка в сечении: плоская нижняя грань и радиусная верхняя грань. Сама передняя кромка отнюдь не острая, а имеет весьма конкретный малый радиус, тем самым улучшая аэродинамику дозвукового полёта. Управление наклоном предкрылка к набегающему потоку позволяет оптимизировать режим образования отрывного пузыря на низких скоростях, создав условия для его безотрывного схлопывания. Так же, учитывая фигуры высшего пилотажа с возможностью длительного полёта вверх ногами, отклоняемый вверх предкрылок позволяет сделать обратный прогиб плоского тонкого крыла для вполне эффективного полёта в перевёрнутом положении, хотя и с худшей аэродинамикой, чем в нормальном положении. На более поздних самолётах Су-35 и Су-57 передняя кромка острее и более симметрично клиновидная, так как рассчитана на более длительный сверхзвуковой полёт.
Вихреобразование и вихревое сопротивление крыла
В сети можно найти массу объяснительного материала по любому вопросу, в том числе и к Вихреобразованию на крыле самолёта, например такой:

В тоже время в том же интернете легко найти Фотографии вихревых следов от самолётов в облачных слоях, которые демонстрируют гораздо больший масштаб явления, чем это нам пытаются показать в теории.

Фото.4. Вихревой след в слое тумана за летящим на высоте самолётом. Кольца видимого туманного вихря отстоят от самолёта на сотни метров, а визуальная близость – это оптическая иллюзия, созданная длиннофокусным телеобъективом при съёмке самолёта с дистанции в несколько километров.

Фото.5. Вихревой след в слое тумана за летящим на высоте самолётом. Виден вертикальный поток воздуха и заходящие с боков волны воздуха, закручиваемые в спираль при соприкосновении с вертикальным нисходящим потоком.

Фото.6. Вихревой след в слое тумана над ВПП за приземляющимся самолётом.
Эти огромные спутные вихри за самолётами формируются вовсе не за счёт концевых вихрей на крыле. Концевые вихри существуют, конечно, но их роль не так велика и с ним активно и успешно борются конструкторы самолётов.
Крупномасштабные вихри с фотографий формируются уже далеко за самолётом, когда волна воздуха, отброшенная самолётом вниз, замещается с двух боковых сторон перетоком воздуха из-под нисходящего слоя в разреженное пространство сверху (см.фото.4-5).
Шедевральное видео про визуализацию вихря за самолётом. В переувлажнённом воздухе конденсат выпадает во всём объёме воздуха за самолётом, тем самым визуализируя масштабное аэродинамическое явление в процессе реального полёта, лучше чем дымами в АДТ.
dzen.ru/video/watch/63badf7a0f646d4b9a595f89
Как альтернатива в сухом воздухе нет следа даже от работы двигателя (см.видео) dzen.ru/video/watch/64c68a149ab9276d36a64f22
Это объяснение образования спутного вихря перекликается с уже рассмотренным вопросом «зоны влияния крыла на окружающее пространство». При этом роль земной поверхности заключается в Границе распространения вниз отброшенного крылом вниз потока воздуха. То есть полёт самолёта и создание «подъёмной силы крыла» возможен и при отсутствии твёрдых подстилающих поверхностей, но при этом отброшенный вниз поток воздуха будет бесконечно долго двигаться вниз, по мере удаления теряя скорость и кинетическую энергию, но сохраняя неизменным вертикальный импульс. Кинетическая энергия первоначальной отброшенной массы воздуха будет теряться на вовлечение в движение боковых потоков воздуха, симметричная разнонаправленность которых не будет изменять исходный суммарный импульс, созданный крылом самолёта. Наглядной иллюстрацией роли Земли-Ограничителя является Фото.6. Там прямолинейный ток тумана над садящимся аэробусом (см.фото.6) опускается до земли по прямой и только потом далеко за самолётом начинается сдвиг в стороны вдоль земли-ограничителя, а слои тумана с боков и сверху уже надвигаются в середину спутного слоя, закручиваясь в двойную самокомпенсирующуюся спираль о нисходящий поток.
«Экранный Эффект» при полёте крыла вблизи Земли
В свете изложенной роли Земли при формировании «Подъёмной силы крыла» имеет смысл дополнительно рассмотреть «Экранный Эффект», который без наличия твёрдой земной поверхности не может возникнуть. Таким образом, физика Полёта крыла в Бескрайнем воздушном пространстве и на «Экранном Эффекте» вблизи Земли имеет весьма различную природу.
Объяснения эффекта «Экраноплана» исходя из сжимаемости газа при малых числах Маха
Влияние близко расположенной поверхности земли на подъёмную силу крыла называют «экранным эффектом». При этом эффекте резко повышается подъёмная сила крыла при полёте вблизи твёрдой поверхности (земля, вода) на высоте сопоставимой с величиной хорды крыла. Основываясь на этом эффекте даже появился целый класс низко летающих аппаратов- «Экранопланов».
В чём же суть явления? Разобраться с этим вопросом можно только предположив, что воздух является Сжимаемым газом.
Тогда при полёте крыла над поверхностью земли образуется воздушный зазор ограниченного размера между двумя твёрдыми поверхностями. При полёте крыла с небольшим положительным углом атаки встречный поток воздуха под крылом испытывает постепенное сжатие от передней кромки крыла к задней кромке (см.рис.8).
Максимальное давление сжатия об экран потока под крылом зависит только от скоростного напора относительно летящего крыла, и это давление в сжатом слое не может превысить давление скоростного напора воздуха:
Ро=Vо^2*Q/2,
где Ро- скоростной напор воздуха при скорости крыла Vо, Vо-скорость полёта крыла, Q-плотность воздуха.
Зная максимальное приращение давления под крылом, рассчитаем геометрические параметры в зазоре «воздушной подушки».
Так при скорости 40 м/с (144км/ч) скоростной напор Ро= 1кПа или 1% от 1атм. (100кПа).
То есть на скорости 40 м/с максимальное давление под крылом достигается при сжатии на 1% по высоте Х зазора от передней кромки крыла к задней. На глаз такое поджатие практически необнаружимо, а слой под крылом визуально кажется плоским (см.рис.8.а).
При этом угол атаки составит А=(Ро/Ратм)*Х/В радиан (при малых углах sinA=A),
где В- хорда крыла, Х- величина воздушного зазора до земли под крылом на уровне задней кромки крыла, Ро- скоростной напор воздуха при скорости крыла Vо, Ратм- атмосферное давление (на уровне моря Ратм= 100кПа).
Получается, что максимально эффективный угол атаки для получения экранного эффекта зависит от высоты полёта крыла над поверхностью, конструктивной ширины крыла и заданной скорости полёта, а угол атаки оказывается лишь производной этих величин.
Вывод: Можно почти бесконечно наращивать ширину крыла, сводя угол атаки почти к нулю, тем самым достигая минимального сопротивления Сх при практически обнуленной индуктивной составляющей сопротивления.
«Экранный эффект» на низких скоростях полёта обеспечивает очень высокое качество крыла, так как создаёт максимальную удельную подъёмную силу на крыле, равную скоростному напору Ро при крайне малых углах атаки на практически плоском и очень тонком крыле. Качество крыла на малых числах Маха при полёте на экране может достигать величины К=25-30.
Вклад разрежения над верхней выпуклой поверхностью крыла при таком полёте на «экране» с плоским крылом достаточно мал в сравнении с давлением под крылом.
При повышении скорости полёта скоростной напор растёт квадратично, а для получение максимального экранного эффекта приходится задирать угол атаки пропорционально росту скоростного напора Ро.
То есть наращивание скорости Vо с целью увеличения Ро влечёт Квадратичное к росту скорости увеличение Угла атаки, что в свою очередь резко снижает качество крыла. И начиная с некоторой скорости Vо-max величина экранного эффект с большим углом атаки сравнивается с подъёмной силой обычного авиалайнера в посадочном режиме с выдвинутой механизацией крыла.
Для любого крыла с хордой В для увеличения высоты полёта Х необходимо задирать угол атаки, после чего Экраноплан поднимется на некоторую новую высоту Х2, где опять установится баланс степени поджатия струи за счёт нового угла атаки на новой высоте. При этом с увеличением высоты полёт экраноплана начинает линейно возрастать сопротивление полёту и соответственная ему потребная сила тяги тоже возрастает без изменения скорости полёта. То есть топливная экономичность полёта экраноплана может разительно изменяться от подъёма по высоте всего на несколько метров. Например, максимальная дальность полёта экранолёта «Иволга» на высоте 0,8 м составляет 1150 км, а на высоте 0,3 метра с той же нагрузкой — уже 1480 км.

Рис.8. Конфигурация воздушных потоков на «Экранном эффекте»: а.) Оптимальный угол атаки без застойной зоны под крылом, б.) Избыточный угол атаки, формирующий большой пузырь застойного воздуха повышенного давления между крылом и поджатым слоем воздуха «Экранной воздушной подушки».
Вывод: Дополнительное задирание угла атаки крыла без увеличения скорости полёта на экране не даёт приращения подъёмной силы, а лишь увеличивает сопротивление полёту Сх (см.рис.8.б)
Считая угол хорды крыла авиалайнера в посадочном режиме около 15 градусов можем оценить величину сжатия струи под крылом до давления Ро и соответствующей ему скорости Vо, считая при этом величину хорды В равной высоте полёта крыла Х.
15 градусов соответствует sin15= 0,262
При угле атаки 15 градусов должен быть скоростной напор Ро=0,26атм= 26кПа, но такие давления реализуются на очень высоких скоростях (740км/ч) и намного превосходят необходимые для полёта расчётные нагрузки на крыло. То есть такой большой Посадочный угол атаки для создания экранного эффекта над ВПП является избыточным на посадочных скоростях 250-300 км/ч.
Качество крыла при угле атаки 15 градусов упадёт до величины всего К=3,7.
Посадочная скорость авиалайнера всего около 250км/ч (70м/с), при этом скоростной напор составит Ро=3кПа или всего 3% от Ратм, тогда как нормальна расчётная нагрузка на крыле в полёте составляет 5кПа (500кг/м.кв=5% от Ратм). То есть при посадке экранный эффект у авиалайнера начинает заметно ощущаться пилотом на высоте соизмеримой с шириной крыла В, сопоставимой с высотой стоек шасси. Выравнивание самолёта и снижение угла атаки для скорости 250км/ч позволяет самолёту пробить «экранную воздушную подушку», так как её несущая способность оказывается ниже, чем потребное давление под крылом для полёта.
За счёт «Экранного эффекта» возникает «Несажаемость» у самолёта в горизонтальном полёте без выпуска механизации крыла при угле атаки 5% (или 3 град.) при скоростном напоре Ро=5кПа, что соответствует Vо=324км/ч или 90м/с.
Угол атаки 5% (или 3 град.) создаёт качество крыла экраноплана равное К=20.
Высокий К=30 соответствует углу атаки в 3% (2 град), при этом подпор под крылом составит всего 3% * Ратм = 3кПа (300кг/м.кв), что соответствует скоростному напору при Vо=70м/с (250 км/ч).
Таким образом, экономически эффективные режимы полёта в режиме «экраноплана» в сравнении с обычным высотным «самолётом» лежат в зоне малых скоростей. При падении качества крыла экраноплана ниже К=20 выгоднее использовать для транспортировки обычный высотный самолёты. То есть экономически выгодные области эксплуатации Экранопланов соответсвуют скоростям ниже 300км/ч.
Маневрирование Экраноплана
Отдельного рассмотрения заслуживает вопрос маневрирования Экраноплана в полёте. Так как подъёмная сила крыла на «экране» формируется иначе, чем при высотном полёте, то и маневрировать «по- самолётному» экраноплан не может.
Экраноплан не может закладывать виражи с креном на крыло, так как он немедленно получит потерю подъёмной силы на задранном крыле и касание воды опущенным крылом. Для экраноплана поворот возможен только «блинчиком», то есть совершенно без крена, а только за счёт создания боковых сил от вертикального оперения.
Само вертикальное оперение Экраноплана тоже должно отличаться от самолётного оперения. Вертикальное оперение Экраноплана должно состоять как минимум из двух килей, способых работать как синхронно, так и вразнобой, что зависит от типа выполняемого манёвра. Вертикальное оперение при этом не только осуществляет разворот Экраноплана вокруг его вертикальной оси, но и создаёт горизонтальную силу поперёк направления скорости полёта.
Горизонтальное оперение на заднем киле выполняет регулирование по углу атаки.
Широкое и короткое крыло необходимо оснащать развитыми концевыми шайбами-скегами, удерживающими спресованый под крылом поток от растекания в стороны. Дополнительно эти шайбы-скеги выполняют роль посадочных понтонов для приводнения.
Также нужно дополнительное горизонтальное оперение на концах основного крыла для компенсации опрокидывающего момента от действия вертикального оперения.
Практически по такой Схеме был построен экраноплан Бартини ВВА-14 (см.рис.9) и многочисленные версии перспективных макетов экранопланов-самолётов, где роль переднего вертикального оперения выполняют скеги-концевые шайбы (см.рис.10).

а.

б.

в.
Рис.9 Экраноплан Бартини ВВА-14. а.Чертёж. б. Модель в 3-Д. в. Фото действующего образца на воде.

Рис.10. Макет перспективного большого экраноплана.
Типы манёвров экраноплана за счёт вертикального оперения:
- Два одинаковых разнесённых киля обеспечивают режим «Сдвиг вбок» при синхронном повороте в одну сторону. При этом Экраноплан как бы сдвигается из одной полосы движения в другую без вращения корпуса. При этом горизонтальное оперение работает разнонаправлено, компенсируя кренящий момент от вертикального оперения.
- Если кили повернуть в разные стороны на одинаковый угол, то возникнет поворачивающий момент, вращающий корпус Экраноплана вокруг вертикальной оси. При этом горизонтальное оперение не работает, так как момента от вертикального оперения не возникает.
- Если кили повернуть в разные стороны на разные согласованные углы, то возникнет поворот по круговой траектории (циркуляция), где вектор скорости совпадает с направлением продольной оси фюзеляжа Экраноплана, а сам экраноплан летит по заданной круговой траектории с равными угловыми скоростями полёта и вращения самого экраноплана вокруг вертикальной оси.
При этом горизонтальное оперение работает разнонаправлено, компенсируя кренящий момент от вертикального оперения.
Все эти режимы практически мало реализуемы в ручном режиме, так как малая высота полёта просто не оставляет времени на реакцию в темпе человеческого восприятия. Для управления Экранопланом нужна автоматизация управлением, подобная автоматической стабилизации сверхнеустойчивых истребителей 4-5 поколения.
Заключение
Все выше сказанные предположения строятся на открыто опубликованных экспериментальных данных (полученные на АДТ эпюры давления на крыле и другие данные).
В экспериментальную Аэродинамику за последний век вбуханы огромные деньги на строительство АДТ различных типов и размеров, так же получен огромный объём фактического материала в экспериментах с макетами различных летательных аппаратов и отдельных элементов крыла.
Вызывает удивление тот факт, что в процессе обучения студентов опираются не на материалы реальных Экспериментов, а на сомнительные теории 100 летней давности. И это при том, что сами экспериментальные данные явно противоречат, этим замшелым Теориям.
Даже в таком обобщённом вводном курсе, как «Введение в Аэродинамику» для ФАЛТ Физтеха, качественные объяснительные модели базового понятия «Подъёмной Силы Крыла» не даются, а вытеснены заумным наукообразным жонглированием математическими формулами (которые к тому же не позволяют ничего рассчитать).
В науке наметился тренд к расколу между теорией и практическим инженерным приложением в разработках конкретных изделий. Явные противоречия в Теоретических моделях не афишируются, а наоборот всячески замалчиваются, дабы не поколебать авторитет замшелых и уже покойных старцев из академии наук и не прервать победного шествия их искренних заблуждений по страницам вполне современных учебников и монографий.
P.S. После публикации первой части этой статьи в обсуждение под статьёй пришло сообщение, что приблизительно те же идеи были высказаны ещё в 2003 году профессором Кембриджа, преподающим там курс «Аэродинамики». В сообщении была дана ссылка на видео с лекцией профессора на эту тему, а также ссылка на статью, где на последней странице описан ровно тот же способ формирования давления изгибаемой струёй воздуха, что и я изложил в данной статье.
Меня несказанно обрадовало, что теперь мне не требуется отбиваться от всех нападок самому, а можно просто сослаться на Кембриджского профессора и его статью в британском научном журнале от 2003г.
Вот сообщение с сылками:
"
JoeHopkins7
24 февраля 2019 в 22:35
–1
Просматривая различные видео про аэродинамику, я наткнулcя на интересную лекцию по аэродинамике профессора Кембриджа.
Ещё в 2003г Кембриджский профессор излагает студентам на лекции ровно те же мысли, что и автор обсуждаемой здесь статьи.
У меня даже закрались подозрения, что автор просто плагиатор.
Но так как он на английских учёных в статье не ссылался, и для своей защиты этих видео в обсуждении не приводил, то можно поверить в его честном самостоятельном открытии чужого открытия.))
Вот ссылка на лекцию
www.youtube.com/attribution_link?a=nfUWqs-6T7M&u=%2Fwatch%3Fv%3DH2RRiF24L4A%26feature%3Dshare&fbclid=IwAR2NOfdqNs0HK9WbCp-OYwy0Y4LYK0ajPPcqV_TCHVqDPOl7yqFpoMfsQ68
Там же есть ссылка на статью, где ещё в 2003году профессор кембриджского университета в английском научном журнале пишет ровно тоже самое, что и автор статью на Хабре
www3.eng.cam.ac.uk/outreach/Project-resources/Wind-turbine/howwingswork.pdf
.."
Подёмная сила крыла. Часть 2
Монин Илья Алексеевич, к.т.н., imoninpgd@gmail.com
Для понимания порядка развития «авиации» как отрасли промышленности и «аэродинамики» как науки нужно вспомнить, что сначала появились первые самолёты, построенные энтузиастами-инженерами по наитию (см.рис.11), а уж только потом начали появляться теоретики, создавшие за тем дисциплину «Аэродинамика» на основании результатов творения инженеров-конструкторов.
На картинке самолёт созданный автомобилистом Анри Фарманом переделкой из купленного мелкосерийного самолёта Вуазена. При этом исходный самолёт братьев Вуазенов начал производится только в 1907г. На момент покупки Фарманом самолёты Вуазена могли приразгоне только слегка подпрыгивать и пролетать при этом несколько десятков метров. Фарман, после ряда переделок исходного самолёта, добился возможности пролететь более 1000м, при этом ещё развернуться и, сделав круг, совершить посадку. Произошёл рекордный полёт Фармана 13 января 1908г. А уже в 1909 году фирма братьев Фарман открывает своё производство самолётов собственной конструкции и лётную школу по обучению искусству полёта на них (см.рис.12). Скорость полёта самолётов Фармана тогда составляла около 60км/ч, которая была показана в рекордном полёте на дистанцию 180км, преодолённую за 3 часа полёта.

Рис.11. Макет самолёта Вуазена, переделанного под рекордный полёт Фарманом в 1907-1908гг.


Рис.12. Макет самолёта «Фарман IV-1910.» в музее, и фото подлинного образца на аэродроме.
Понятно, что первые ранние самолёты были маломощные, лёгкие и низкоскоростные.
Именно этим параметрам соответствуют первые выпукло-вогнутые тонкие профили, больше похожие на простейший изогнутый лист фанеры, а не на сложный профиль с глубоким теоретическим просчётом.
Для справок привожу иллюстрацию трансформации профилей крыла от самых ранних начала 20-го века, до вполне развитой авиапромышленности середины 40-х годов. (см.рис.13)

Рис.13. Тенденции изменения профиля крыла самолётов первой половины 20-го века.
После первых лёгких экспериментальных самолётов последовал Быстрый рост размеров и массы самолётов для перевозки всё большей полезной нагрузки. Тонкие крылья уже никак не могли выдержать такого размаха и веса, что потребовало внутрь крыла устанавливать высокие прочные балки, а само крыло сделать плоско-выпуклым или даже двояко выпуклым, чтобы скрыть несущую балку за обтекаемой подшивкой крыла.
Уже в 20-х годах все профили крыла приняли вполне современный вид.
К 1940-м годам авиационная индустрия настолько развилась, что начала производить целые армады самолётов, способных с воздуха разносить в труху целые города. Но при столь взрывном развитии производственных мощностей теоретическая база оставалась крайне слабой.
К 30-м годам интенсивность развития авиации уже не позволяла строить новые самолёты по «наитию», а потребовало строительство мощной экспериментальной базы по продувке частей самолётов, масштабных макетов и самолётов целиком на земле в огромных аэродинамических трубах (АДТ).
Так в ЦАГИ в 1939 году была запущена крупнейшая на тот момент (вторая в мире сейчас) аэродинамическая труба Т-101, позволявшая на земле исследовать самолёты целиком на актуальных в то время скоростях полёта.
Скорость потока 5–52 м/с
Число Re на 1 м до 3.6∙106
Полное давление атмосферное
Скоростной напор до 1.7 кПа
Температура торможения окружающей среды
Диапазон углов атаки (α) ±20°
Диапазон углов скольжения (β) ±180°
Размеры рабочей части:
Сечение сопла (эллипс) 24x14 м
Длина рабочей части 24 м
Размеры объектов испытаний:
Размах крыла: до 18 м
Длина фюзеляжа: до 30 м
Площадь крыла: до 35 м2
С тех пор самолёты стали много крупнее, а скорости полёта много быстрее, так что уже ни один современный самолёт не влезает в АДТ Т-101 целиком, а в более современных и более скоростных АДТ продувают только масштабные уменьшенные макеты или элементы конструкции по отдельности.
Правда, в теории с начала прошлого века изменилось мало, так что уже в конце двадцатого века авиаконструкторы начали заново изобретать то, что уже прошли конструкторы начала-середины 20-го век, но так и не объяснили теоретики. Для примера приведу вид профиля крыла пилотажного самолёта, считавшимся лучшим ещё в 1980-х годах (см.рис.14).

Рис.14. Один из профилей крыла самолёта из каталога «Авиационные профили».
Такой же возвратный ход мысли наблюдается и среди крупных образцов лётной техники, это выразилось в создании монстров-экранопланов в 1960-80-х (рис.15), мало отличимых от гигантских самолётов конца 1930-х (рис.16).
При этом сам экранный эффект был обнаружен ещё в начале 30-х в моменты посадки крупных многомоторных самолётов с большой хордой крыла.
Так же экранный эффект ярко проявился при посадке рекордного дальнего самолёта АНТ-25, когда при испытательном полёте в 1933 году самолёт просто не мог приземлиться, а при лёгком касании колёсами земли самолёт подпрыгивал и снова взлетал. Чтобы убрать этот эффект и обеспечить спокойную посадку пришлось даже устанавливать специальные выдвижные тормозные щитки, резко ухудшающие лётные качества крыла во время посадки.
Хорда крыла в наиболее широкой корневой части у АНТ-25 превышала высоту стоек шасси, таким образом, создавались идеальные условия для формирования экранного эффекта под широким низколетящим крылом. При это во время посадки с пустыми баками при массе самолёта 4000кг и площади крыла 88м.кв, средняя нагрузка на крыле в полёте создавалась менее 50кг/м.кв, что соответствует скоростному напору 500Па создаваемому при скорости 104км/ч (29 м/с) для полёта на экране. Стоит заметить, что самолёты того времени летали крайне медленно (по современным меркам), так рекордный АНТ-25 имел крейсерскую скорость около 165км/ч (макс.246км/ч на высоте), при дальности полёта 10-12тыс.км и длительности 75-80 часов подряд.
А.

Б.

В.

Рис.15. Экраноплан «Каспийский Монстр»: а.) В полёте. Б.) Неподвижно на воде анфас. в.) Неподвижно в лобовой проекции.
А.

Б.


Рис.16. Самолёт-гигант АНТ-20 «Максим Горький», 1939г. а) Схематичный разрез. Б) Фото на аэродроме и при посадке.
Застойные зоны при Обтекание воздухом тел сложной формы как инструмент формирования виртуального профиля крыла.
Часто встречаются случаи. Когда необходимо построить линии тока воздуха вокруг тел, форму которых трудно назвать обтекаемой.
Понятно, что воздух не станет послушно обтекать все углы и выемки тела, а пойдёт мягкими извивами, проносясь над ямами и заполняя их вихрями оторванных потоков застойных зон.
Если учесть наличие застойных зон как дополнительных твёрдых объёмов самого профиля, то геометрия Обтекания известных нам аэродинамических элементов примет совершенно иной вид.
Интересно, что такой метод нахождения эквивалентного условного прототипа крыла используется и в существующей прикладной Аэродинамике. Во всяком случае метод построения «Фиктивного полубесконечного тела» вокруг твёрдого крыла описывается в учебнике[3] на целых трёх страницах(стр.435-437), при этом в качестве границ фиктивного крыла выбирают границу толстого заторможенного пограничного слоя, то есть прибавляя к крылу те самые наши застойные зоны в «отрывных пузырях» или турбулентне зоны при полном срыве потока над крылом. При этом давление на твёрдое крыло от скоростного потока воздуха считается равным давлению этого потока на «фиктивное тело». Получается, что давление передаётся от скоростной струи на твёрдое крыло через достаточно толстый слой малоподвижного воздуха пограничного заторможенного слоя (застойной зоны) без каких- либо искажений.
Рассмотрим детально процесс мягкого обтекания скоростными струями разной интенсивности профилей крыла и выделим различные «застойные зоны».
Случай полного прилипания потока к крылу на малых углах атаки особой новизны не прибавляет (см.рис.17), но появляется маленькая застойная зона на лобовом обтекателе, напоминающая маленький острый клюв на круглой голове птицы.
Элемент кажется небольшим, но он крайне важен для понимания явления «обтекания» в целом.
Рассмотрим привычный профиль крыла в горизонтальном полёте с выраженными отрывными струями сначала с нулевым углом атаки(см.рис.18), а затем это же крыло уже под большим углом атаки(см.рис.20).

Рис.17. Профиль крыла с обтеканием без отрывов на плоскостях крыла, но с маленькой зоной полного торможения потока на носовой части крыла.

Рис.18. Профиль крыла с отрывов потоков на плоскостях крыла при нулевом угле атаки и его «Фиктивное тело».
Глядя на сильное увеличение «Фиктивного тела» в сравнении с исходным расталкивающим лобовым обтекателем становится понятно как получается удивитльно низкое лобовое сопротивление у длинных веретёнообразных тел, на-пример, у фюзеляжей самолётов.
Обтекаемость таких форм достигает величины Сх=0,06, тогда как для шара такого же сечения Сх=0,4..0,5, а для плоской пластины Сх=1.
Оказывается в разряжении под отрывными струями в лобовой проекции сопротивление не создаётся совсем. Остаётся только приземлить отрывную струю на паралельную к вектору скорости прямую поверхность, чтобы при ударе не возникла продольная к скорости составляющая. С такой задачей прекрасно справляется длинный цилиндрический фюзеляж с вытянутым яйцевидным лобовым обтекателем. Получается, что лобовое сопротивление огромного фузеляжа равно сопротивлению шара на оконечности суживающейся носовой части (см.рис.19.)
Соотношение диаметра шара в носовом обтекателе к диаметру фюзеляжа зависит от скорости полёта, и чем выше скорость полёта, тем зауженней становится носовое скругление, расталкивающее воздушный поток. Возрастающая энергия встречного потока при постоянной величине лобового сечения требует разбрасывать всё меньшее количество воздуха в стороны от фюзеляжа при сохранении постоянного сечения «фиктивного тела» за обтекателем. На сверхзвуке радиус кривизны носового обтекателя вырождается в остриё, но это уже совсем другая история.



Рис. 19. Режим обтекания фюзеляжа с отрывными струями, под которыми создаётся зона нулевого сопротивления полёту. Всё сопротивлении фюзеляжа равно аэродинамическому сопротивленю шара в его носовом обтекателе. И сопровоодительные иллюстрации из учебников на тему сравнения сопротивления при обтекании воздухом различных тел .
Теперь рассмотрим поведение отрывных турбулентных зон при крыле с большим углом атаки (см.рис.20).
Сначала необходимо проследить траекторию отрывного потока над застойной зоной до момента встречи с потоком из под крыла самолёта. Так как профиль лобового обтекателя крыла считаем симметричным цилиндрическим, то и отрывные струи имеют равную мощность и траекторию, то есть тоже симметричны.
Для горизонтального крыла мы уже получили симметричный двусторонний отрывной пузырь с замыканием струй на крыле в одинаковых местах.
При придании крылу большого угла атаки картина отрывных струй меняется. При этом размеры «Отрывных пузырей»= «Застойных зон» над и под крылом начинают разительно отличаться по объёму.
В итоге в качестве «фиктивного тела» получится очень сильно распухшее крыло со значительным уплощением нижней плоскости по сравнению с огромным куполом отрывного пузыря на верхей плоскости крыла. Интересно, что эквивалентный виртуальный профиль «фиктивного тела» на большом угле атаки крыла с раздутыми отрывными пузырями на верхней плоскости крыла удивительно похож на известный летательный аппарат ЭКИП. (см. рис.21)

Рис.20. Профиль крыла с отрывов потоков на плоскостях крыла при большом угле атаки и его «Фиктивное тело».



Рис.21. Экраноплан ЭКИП. Макет перспективного образца Экраноплана и действующая уменшенная модель Экраноплана (так и не взлетевшая из-за остановки проекта).
То есть в Экранолёте ЭКИП предлагалась вполне здравая мысль по контролю застойной зоны в задней «теневой» части корпуса, что позволяло осаживать отрывную струю на крыло в верхней части купола, что даёт большую подъёмную силу и уменьшает аэродинамическое сопротивление полёту.
Выходит, что автор ЭКИПа был не таким уж и выдумщиком, предлагая в качестве летательного аппарата такую бегемотоподобную конструкцию.
Правда летать ЭКИП должен не очень быстро и на больших углах атаки исходного тонкого профиля (около 15 градусов), с соответствующим высоким лобовым сопротивлением.
Огромный объём грузового пространства в таком летающем крыле с лихвой может скомпенсировать некоторое ухудшение аэродинамики. При этом конструктивно безфюзеляжный Самолёт-Крыло выглядит гораздо привлекательней, чем традиционный самолёт с разделением функций тонкого «несущего крыла» и «грузо-пассажирского фюзеляжа». Вот только для стабильного полёта ещё придётся добавить длинную балку для размещения хвостового оперения, как на гигантском летающем крыле АНТ-20 «Максим Горький».
Значительное расширение крыла (увеличение хорды) делает Самолёт типа ЭКИП ещё и ярко выраженным Экранопланом по своим аэродинамическим свойствам при полёте вблизи земли. Так при полёте на экране «фиктивное тело» крыла с большим углом атаки трансформируется в странный утюг, где маленький носовой клюв зоны торможения на крыле раздувается до размеров огромного застойного клина под крылом (см.рис.22).
Образование такой мощной застойной зоны под крылом с большим углом атаки хорошо видно на стопкадре (см.рис.22-2). Сссылка на видео целиком www.youtube.com/watch?v=Sd4ycAtYcJA. Хорошо видно в трёх ракурсах одновременно как дымовые шнуры от двигателя огибают лобовой обтекатель снизу вверх и на равном удалении от крыла огибают всю плоскость крыла сверху.

Рис.22. Профиль крыла при полёте над экраном при большом угле атаки и его «Фиктивное тело».

Рис.22-2. Дымовые шнуры от двигателей, затекающие из под крыла Боинг-747 в момент отрыва от ВПП на взлёте.
Внутрь этого остроносого утюга можно разместить как профили Экранолётов ЭКИП и ВВА-14 (Бартини), или сверхтолстое крыло как у АНТ-20 «Максим Горький».
Самолёты с очень толстым крылом были популярны в 1930-х годах в СССР, когда был создан самый крупный довоенный самолёт АНТ-20 «Максим Горький». У этого самолёта крыло было на столько толстым и широким, что в корневых отсеках крыла помещалось несколько кают, где человек ходил в полный рост (см. Рис.16.).
Правда, летал этот монстр с крейсерской скоростью всего 198км/ч (максимум 220км/ч).
Если у АНТ-20 чуток укоротить концевые участки крыла, оставив только центральную наиболее толстую часть, то самолёт станет похож на более поздний Экраноплан «Каспийский Монстр» Ростислава Алексеева.
Интересно сравнить близкие по размерам «Максим Горький» из 1930-х с «Каспийским Монстром» из 60-х (см.таб.5)
Таб.5. Сравнительные характеристики самолёта АНТ-20 «Максим Горький» 1934г. и Экраноплана КМ «Каспийский Монстр» 1966г.

В таблице представлены справочные данные, которые надо как-то интерпретировать.
Пойдём сначала простым путём прямого сравнения однородных цифр делением друг на друга.
Масса максимальная: 544/42= 13 раз
Площадь крыла: 662/486=1,36 раза
Удельная нагрузка на крыло: 13/1,36=9,5 раз
Скорость крейсерская: 430/198=2,17 раза
Различие скоростных напоров на крейсерской скорости: 2,17^2= 4,71раза
Мощность энергоустановок: (10*1300*9,81*430/3,6) /(8*900 000*0,735)=28,8 раз
Грузоподъёмность с учётом топлива: 304/(42-28,5)= 22,51.
Практическая дальность: 1500/1200=1,25
По соотношению топливной экономичности АНТ-20 = 7150/(1200*6)=0,993 л/(т*км)
Прожорливость КМ не известна, но можно её оценить через мощность и скорость.
При расчёте на удельный расход по справочной прожорливости 0.8кг/(кгс*ч) для двигателя ТРД ВД-7.
Расход на форсаже при разгоне с воды 10*13000*0,8=104 000кг/ ч
Если учесть длительность крейсерского полёта на экране только с двумя работающими моторами из десяти имеющихся для разгона и выхода на Экран, то экономичность повысится.
Для крейсерского полёта с двумя двигателями 2*13 000*0,8=20 800кг/ ч
Время полёта 1500/430=3,5часа
За полёт на максимальную дальность 1500км КМ сожрёт не менее 104*0.5+3,5*20,8=100тонн топлива.
А полезная нагрузка составит около 200 тонн.
Топливная экономичность КМ получится 100 000/(1500*200)=0.333 л/(т.км).
Выводы из полученных соотношений:
1. По топливной экономичности КМ может в оптимистичном варианте оказаться в 3 раза экономичнее, чем АНТ-20.
Сейчас у современного авиалайнера Аирбас А380 предусмотрена грузовая модификация A380F с возможностью перевозить груз до 150 тонн на расстояние до 10 370 км. Максимальная взлётная масса — 560 тонн (масса самого самолёта — 280 тонн). Расчёт экономичности для грузовой версии делаем из этих показателейдаёт 130тонн топлива 150 тонн груза на дистанцию 10370км: 130000/(150*10370)=0,0835 л/(т*км).
В пересчёте на пассажиров показатель другой: «Среди больших лайнеров самый экономичный — три литра топлива на одного пассажира на сто километров (54 морских миль) пути. По заявлениям Airbus[5], в расчёте на одного пассажира A380 сжигает на 17 % меньше топлива, чем «современный самый большой самолёт» (по всей видимости, имеется в виду Boeing 747). „
То есть при проверочном пересчёте на 850 пассажиров с багажом и креслами получим показатель близкий к расчёту для грузовой версии.
Выходит, что мы не только стали в 4-5 раза быстрее летать за последние 80 лет, но и по топливной экономичности улучшились более чем в 10 раз от АНТ-20 и в 4 раза от Экраноплана КМ. Хотя всего 20 лет назад наши аэробусы летали в 5 раз быстрее, чем АНТ-25. Недавнее снижение скорости в пассажирской авиации вызвано борьбой за топливную экономичность полёта.
2. Крейсерская скорость у КМ сделана столь высокой вынужденно, так как на меньшей скорости он просто не сможет лететь на экране. Условие полёта на экране- это выполнение неравенства «Скоростной напор» > «Средняя нагрузка на крыло», то есть
Pv= 8560Па при 430км/ч(120м/с) > 544000*9,81/662,5=8055Па.
3. Полётная безопасность тихоходного Самолёта-Гиганта из 30-х сильно лучше, чем у избыточно скоростного экраноплана из 60-х, почти неуправляемо несущегося среди тихоходных судов и вездесущих водных птиц.
4. Стоимость эксплуатации водоплавающих по морю экранопланов значительно дороже, чем для сухопутных высотных самолётов. Это связано с избыточным количеством двигателей, нужных только для старта с воды и выхода на экранный полёт, а также из-за чрезвычайной агрессивности морской воды при воздействии на двигатели и конструкции экраноплана при полёте в облаках брызг от близких морских волн.
5. Для Экраноплана КМ легко считается качество крыла при полёте на двух двигателях, равное отношению их тяги к весу самого экраноплана К=544/(13*2)=20,9. Таким образом, аэродинамическая эффективность большого и тяжёлого Экраноплана находится на уровне экономичность лучших современных крупных самолётов с качеством планера порядка К=18-20.
6. Загадкой для меня остаётся трёхкратный разрыв по экономичности Экраноплана КМ с Аэрбас 380F: Почему при равном качестве планера у Аэрбаса в 4 раза лучше топливная экономичность?
Или вся тайна кроется в жуткой прожорливости старых советских турбореактивных двигателей в сравнении с современными турбовентиляторными двигателями высокой степени двухконтурности?
Подъёмная сила крыла. Часть №3.
Послесловие к Части № 1-2.
Прошёл ровно год после первой пуликации на Хабре моей статьи (4.02.2019) про объяснение подъёмной силы крыла без уравнения Бернули.
Статья за год набрала боле 41 тысячи просмотров и заняла лидирующее положение в поиски Яндекс на запрос «подъёмная сила крыла», оказываясь в верхней части первой страницы сразу за определением из Википедии.
Так же в личных сообщениях мне было дано множество ценной информации и крайне важных критических замечаний.
Я не буду править ранее написанные части, но проведу разбор некоторых ошибочных заявлений, которые мною были оттиражированы из таких же ошибочных заявлений учебников.
Замечание 1.
Основным замечанием оказалось то, что я ошибочно привёл и неправильно истолковал картинки наглядных сравнений аэродинамических сопротивлений различных тел вращения полёту.
Так я считал это сопротивление соответствующим сопротивлению Сх для поляр самолётов, а на картинке из какого-то учебника (рис.19 во второй части) вообще указано ошибочное обозначение Су вместо Сx.
Мне же объяснили, что на самом деле для отдельных тел вращения будет правомочен коэффициент Cd, который связывает поперечное сечение (мидельное) продуваемого объекта с оказываемым ему сопротивлением скоростным напором.
Величина Cd у лучших гоночных машин не опускается ниже 0,27.
При этом для веретёнообразных тел и профиля крыла без подъёмной силы коэффициент лобового сопротивления заявляют до 0,06..0,04, что для показателя Dх не достижимо никогда.
Такое низкое Су, как 0,06...0,04, не является прямым обманом, но вводит в заблуждение из-за утаивания обстоятельств и нюансов расчёта. Так величина Cd рассчитывается из отношения к поперечному сечению (миделю), а величина Cх рассчитывается из соотношения к наибольшей площади крыла в вертикальной проекции, то есть к наиболшей площади крыла в продольном направлении к действующей силе сопротивления.
Так на красочных картинках, демонстрирующих обтекаемость различных тел в полёте, начинают некорректно сравнивать «Длинное» с «красным», то есть сравнивать величины в несравнимых размерностях.
Реальные же значения лобового сопротивления Сd, отнесённого к сечению по “миделю», cмотрите в таблице ниже.

Таб. Величины лобовых аэродинамических сопротивлений Сd тел различной формы.
Левая таблица- тела вращения. Правая таблица- балки заданного сечения.
Замечание 2.
Хабр- отличный ресурс для публикации научно-технических статей разного профиля, но его правила дают удивительно широкие полномочия «троллям-негативщикам», которые своими дизлайками загоняют карму автора в глубокий минус, лишая его возможности как отвечать на критические замечания, так и делать новые публикации своих статей. Об этой особенности Кармы на Хабре есть даже опубликованные статьи на самом Хабре.
В результате падения моей Кармы ниже -30 я оказался отрезан от права комментировать свои же статьи, а так же лишен права на публикации.
Исключением является эта статья по аэродинамике, где мне каким-то чудом оставлено право на редактирование.
Этой «дырой возможности» я и воспользуюсь для публикации новой части статьи в обход отрицательной кармы.
Все ваши замечания и пожелания вы можете обращать мне в «личные сообщения» на самом Хабре или по адресу моей е-почты imoninpgd@gmail.com, также указанной и в начале каждой моей статьи.
Я всегда с удовольствием отвечаю на личные сообщения с конструктивной критикой в вежливой форме.
Практическое применение тонких изогнутых радиусных крыльев в современных конструкциях.
Как оказалось, расссмотренные в первой части тонкие выпукло вогнутые радиусные крылья сейчас активно используются в качестве поворотных лопаток в больших аэродинамических трубах (см.рис.23, 24)
На рисунке ярко видно, что для поворота потока используют именно такие тонкие лопатки, как и в моей статье.
Нет никаких сомнений, что конструкторы этих поворотных лопаток знают о тех механических нагрузках, которые испытывают данные лопатки от набегающего на них потока.
Также несомненно легко замерить давление на лопатки от искривлённого потока воздуха как на выпуклой, так и на вогнутой части этих лопаток. Причём замер давлений можно осуществить как для одного потока по толщине, так и для для одной лопатки с разных сторон.
Полагаю, что людям, имеющим доступ к АДТ ЦАГИ, не составит больших сложностей снять тензодатчиками давление с лопаток направляющего аппарта АДТ во время одного из текущих экспериментов.

Рис.23. Профиль аэродинамической лопатки, применяемой в современной аэродинамической трубе в качестве наборного поворотно-спрямляющего устройства в воздушном тракте АДТ.

Рис.24.Расположение поворотных лопаток в тракте АДТ в 3Д-визуалищзации.
На фото (ри.25) изображены профили рабочих лопаток ротора газовой турбины из некого учебник по «Гидрогазодинамике», где рассматриваются элементы конструкции энергетических паровых и газовых турбин.
Эти лопатки практически точно повторяют профиль тонкого изогнутого выпукло-вогнутого крыла, описанного в теоретической 1-й части этой статьи, точно также как совпадают методики расчёт нагрузок на лопатки от потока газа в этих учебниках по «Гидрогазодинамике» с изложенной методикой в 1-й части этой статьи.
Отличительной особенностью работы лопаток ротора турбины заключаются в том, что при огибании газом поверхности лопаток сам газ не меняет плотности и температуры, но лишь плавно меняет направление вектора скорости потока газа, не меняя скорости газа по модулю, если рассматривать поток газа в координатах с привязкой к самой лопатке турбины. То есть условия работы отдельной лопатки ротора турбины практически точно воспризводят условия работы одиночного тонкого изогнутого крыла в свободном воздушном пространстве.
Удивительно то, что изложенное мною в статье давно известно и широко используется в прикладных расчётах в «Гидрогазодинамике» при конструировании газовых турбин как для энергетики так и для двигателей самолётов, при этом адепты «Аэродинамики» в упор не замечают эти расчётные и теоретические модели из «Гидрогазодинамики», считая «Аэродинамику» и «Гидрогазодинамику» разными науками с разными законами взаимодействия для совершенно одинаковых твёрдых крыльев с окружающей их одинаковой средой газов и жидкостей.

Рис.25. Профили рабочих лопаток газовой турбины и визуализация потока газов на них.
Подъёмная сила крыла. Часть №4.
Флаттер крыла
В период бурного развития авиации в 1930-х годах в погоне за высокими скоростями неожиданно проявилось удивительное явление, названное Флаттер, когда на определённой скорости самолёта внезапно возникают нарастающие крутильно-изгибные колебания крыльев, за несколько секунд приводящие к разрушению самолёта.
С этой проблемой разобрались конструктивными методами, увеличив крутильную и изгибную жёсткость конструкций крыла, но теоретические объяснения так и остались на уровне «Интуитивно-эмпирических решений», хотя академик Келдыш получил за эти решения Сталинскую премию.
В учебниках по аэродинамике (см. библиографию) я не обнаружил глав, объясняющих флаттер.
Таким образом, я буду давать объяснения явления Флаттера не опираясь ни на какую официальную теорию, а просто выводя следствия из теоретических положений, описанных в первой части статьи.
Как было описано в первой части, на лобовой обтекатель набегает поток, имеющий радиус искривления не менее
Rп=2*Rобт
Где Rобт – радиус скругления лобогого обтекателя крыла.
При этом толщина отклоняемого в каждую сторону от крыла потока равна Нп= Rобт.
Из геометрического построения следует, что угол вектора скорости отрывного потока при касании его обтекателя к направлению полёта равен
А=arccos(2/3)=48 градусов .
Вертикальная проекция скорости отрывного потока равна
Vп. верт=Vп* sin А=0,743*Vп.
То есть мы получили оценку сверху скорости по вертикали для отрывного потока, так как у нас ране уже был получен критерии предельной оценки для радиуса искривляемого потока Rп=2*Кобт
при толщине отклоняемого в одну сторону потока Нп=Rобт.
При дальнейшем движении над искривлённым профилем крыла отрывной поток с исходной энергией
Еп.верт.= Vверт.п^2*q*Rобт
должен погасить её за счёт работы разницы давления окружающего воздуха и давления на поверхности крыла под отрывным течением, то есть за счёт работы давления разряжения над плоскостью крыла.
Евозд= Нотр*Рвозд
То есть должно быть выполнено равенство Еп.верт=Евозд
Vверт.п^2*q* = Нотр* Рвозд
Высоту огибаемого пузыря без срыва потока с профиля:
Нотр= Vп.^2*q* Rобт /Рвозд
Подставляя выражение для Vп. верт=Vп* sin А
получаем:
Нотр= (Vп * sin А )^2*q* Rобт / Рвозд = Vп.^2*q* sin А^2* Rобт/ Рвозд
То есть при высоте профиля выше этой величины обтекание происходит без образования отрывного пузыря.
Если же величина горба профиля за лобовым обтекателем ниже величины Нотр, то обтекание профиля потоком происходит с образование воздушного пузыря с разряжением и застойным воздухом внутри, визуально обнаружимого по колебаниям шелковинок.
Дальше возникает вопрос длины застойного пузыря под отрывным течением.
Если считать перепад давления воздуха постоянным, то торможение потока воздуха будет равноускоренным, а кривая границы отрывного пузыря будет иметь вид параболы горбом вверх.
Время полного торможения потока по вертикали составит
T=V верт/А.верт
Где А.верт=Рвозд/(Rобт*q)
Получаем
Tпуз1=V верт/А.верт= V верт*(Rобт*q)/ Рвозд
Длина отрывного пузыря Lпуз1 до вершины составит
Lпуз1=Vп*Тпуз1= Vп* V верт*(Rобт*q)/ Рвозд= Vп *(Vп * sin 42)*Rобт*q/ Рвозд =>
Lпуз1=Vп ^2*q * sin А*Rобт / Рвозд
Из полученной формулы Lпуз1 для длины восходящей части отрывного течения над отрывным пузырём (или идеальным профилем) можно сделать вывод, что при некоторых значениях скорости полёта Vп и толщины лобового обтекателя Rобт может возникнуть ситуация, что величина отрывного пузыря
L пуз 1+2= 2* Lпуз1
может превысить ширину крыла Вкр.
Когда расширения отрывного пузыря достигает задней кромки крыла, а ниспадаюший отрывной поток уходит за заднюю кромку крыла, тогда под отрывной пузырь попадает воздух с высоким давлением из спутного следа.
После выравнивания давления в отрывном пузыре с атмосферой на отрывной поток перестаёт действовать разница давлений между атмосферой и пузырём над крылом. После чего отрывной поток отрывается от обтекателя и уже не может вернуться обратно на крыло, тем самым создавая полный срыв потока.
При скоростном горизонтальном полёте выше расчётной нормальной скорости для конкретного самолёта при таком срыве потока над верхней плоскостью крыла дальнейшие события развиваются в следующем порядке (см.рис.26):
— Отрывные течения формируют на крыле с малым углом атаки отрывные пузыри разных размеров, при этом общая равнодействующая подъёмная сила крыла Fк1= Fк.верх- Fк.низ, а крутящий момент относительно ЦТ имеет расчётную величину на рычаге L1
— При ускорении до Vф отрывноое течение над верхней плоскости крыла достигает задней кромки, а равнодействующа Fк2 становится больше расчётной Fк1. Также сильно возрастает крутящий момент на крыле от увеличения плеча L2 усиливая момент на пикирование.
— При срыве потока подъёмная сила от разряжения в верхнем отрывном пузыре пропадает.
— При резком исчезновении разряжения над верхней поверхностью крыла возникает мгновенное разгружение конструкций крыла только с одной стороны.
-На нижней плоскости крыла срыв потока ещё не происходит, а потому продолжает действовать значительная аэродинамическая сила вниз от развитого отрывного пузыря, которая по модулю многократно превосходит нормальную подъёмную силу крыла.
Таким образом, происходит резкая перегрузка крыла на изгиб в другую сторону, то есть вниз, с закручиванием крыла на кабрирование.
В результате самолёт резко проваливается вниз, задирая нос и теряя скорость.
При закручивании крыла задней кромкой вниз резко растёт угол атаки всего крыла, в результате чего резко усиливается торможение на поток воздуха, при этом происходит схлопывание отрывного пузыря, а подъёмная сила на нижней поверхности крыла резко меняет знак на подъём, выгибай крыло снова вверх.
При восстановлении нормального направления подъёмной силы крыло начинает резко изгибаться вверх, а момент от вновь созданной нормальной подъёмной силы скручивает крыло и разворачивает крыло со всем самолётом из кабрирования на пикирование.
Таким образом цикл замкнулся и пошёл на второй круг.
Самолёт уходит в разгон, восстанавливается обтекание без срыва потока по верхней плоскости крыла, и после нового достижения критической скорости срыв потока возникает снова, а изгибные перегрузки крыла со скручиванием повторяются.
Вот такая быстротекущая тряска со знакопеременными изгибами и скручиванием крыльев (при нагрузках в разы выше расчётных статических) неизбежно приводит к быстрому разрушению крыльев.

Рис.26. Фазы развития флаттера на крыле:
1) Нормальная подъёмная сила Fк1 до начала флатера, где площадь заштрихованного прямоугольника показывает равнодействующую сил давления на крыло от симетричны отрывных потоков.
2) Избыточная подёмная сила на крыле Fк2 при повышении скорости выше расчётной. От избыточной подъёмной силы Fк2 силы на сильно увеличеном плече L2 образуется сильный крутящий момент на пикирование незадолго до срыва потока с верхней плоскости и начала флаттера.
3) Срыв потока с верхней плоскости крыла при развитом флаттере. На верхней плоскости подъёмная сила исчезает из-за выравнивания давления с атмосферой. Некомпенсированная сила от нижнего отрывного пузыря создаёт перегрузку крыла огромной силой Fк3 в сторону земли, а крутящий момен на крыле резко меняется на кабрирование.
4) При резком увеличении угла атаки крыла набегающий поток воздуха гасит отрывной пузырь с пониженным давлением на нижней плоскости крыла, в результате чего подъёмная сила меняет направление на нормальное, то есть вверх, с востановлением крутящего момента на расчётное пикирование.
Именно такое циклическое быстро повторяющееся крутильно-изгибное колебание крыла на некой критической скорости Vф и называют Флаттером.
Разрушения крыла от Флатера можно избежать путём резкого усиления конструкций крыла. Именно такую рекомендацию на «интуитивно –эмпирическом уровне» дал Келдыш.
При этом усиливается не только прочность по величине выдерживаемых статических нагрузок на крыло, но также усиливается жёсткость крыльев на изгиб и кручение, что позволит понизить накапливаемую во взмахах крыльев энергию, тем самым сделав её ниже пороговой энергии разрушения крыла.
Для увеличения жёсткости на кручение лучше всего применять замкнутый контур типа «труба» или «короб». Более жесткие на кручение «короба» оказываются значительно тяжелей «ферм», применявшихся на тихоходных самолётах ранних конструкций.
В более поздних и продвинутых конструкциях самолётов замкнутым крутильным коробом оказывается вся внешняя толстая листовая обшивка крыла, при этом с применением внутри объёма крыла несущих балок и рёбер жёсткости ферменного или двутаврового типа. Использование листовой обшивки крыла в качестве несущего силового элемента резко увеличивает жёсткость конструкции с одновременным снижением веса всего крыла.
Кстати, в самодеятельном авиастроительстве с плёночной или тканевой обшивкой крыла и сейчас очень часто тонкостенные трубы применяют как основную несущую балку крыла.
Избежать появление флаттера на желаемой к достижению скорости можно за счёт изменения профиля крыла в сторону уменьшения радиуса лобового обтекателя Rобт, что приведёт к повышению величины пороговой скорости Vф для нового профиля крыла.
Согласно сделанных расчётов никак не получится избежать флатера совсем в горизонтальном полёте, но снизить его влияние для достижения предельных скоростных значений вполне возможно.
Таким предельным значением является скорость звук, после которой режим обтекания крыла резко меняется, а флаттер остаётся в дозвуковом скоростном диапазоне.
При сверхзвуковом полёте обе плоскости крыла информационно разделены, так как низкочастотные волны давления (звуковые волны низкой частоты с большой длиной волны) от циклических срывов потока не могут обогнать сверхзвуковое крыло и нарушить однородность воздушных масс перед летящим крылом.
Таким образом, даже если плоскости крыла работают в попеременном режиме полного срыва потока, то после перехода «звукового барьера» трясти самолёт резко перестаёт.
Как рассакзывают лётчики, после перехода звукового барьера после мучительной тряски внезапно наступает тишина.
Именно из-за принципиальной неустранимости флаттера летать на опасных флатерных трансзвуковых скоростях рекомендуют очень короткое время, что достигается быстрым разгоном до сверхзвука на полном форсаже, или быстрым торможением со сверзвука до уровня дофлатерной скорости.
Такими быстрыми проходами флатерного диапазона скоростей обеспечивается минимальная длительность воздействия вибрации от флаттера на конструкции самолёта.
При уменьшении радиуса лобового обтекателя Rобт само явление флаттера не исчезает полностью, но сдвигается в сторону более высоких скоростей.
Так в 1930-х для наиболее скоростных истребителей флаттер был актуален на скоростях 300-400км/ч, когда избытка мощности двигателя хватало разогнать небольшие облегчённые самолёты до критической скорости.
При снижении размеров Rобт на крыле были получены гораздо более скоростные и более высотные истребители, такие как МиГ-3 образца 1940г.
Но платой за скорость для новых скоростных самолётов оказалась меньшая подъёмная сила на низких скоростях, что потребовало бы больших скоростей при посадке.
Но увеличивать посадочные и взлётные скорости на грунтовых аэродромах нельзя!
Чтобы справиться с этой проблемой пришлось в конструкцию крыла новых скоростных самолётов специально для режима взлёта и посадки вводить дополнения в виде отклоняемых пластин — «закрылков» и «предкрылков». Закрылки и предкрылки резко поднимали подъёмную силу крыла на низких скоростях с большими углами атаки, но ухудшали качество крыла.
Так гонка за скоростью и борьба с флаттером привели к утяжелению крыла для упрочнения и усложнения крыла для обеспечения приемлимых скоростей влёта и посадки, что тоже дополнительно утяжелило самолёты.
Для сравнения можно оценить истребитель простой конструкции дофлатерной геометрии И-16 и более скоростной и сложный МиГ-3 (с предкрылками и закрылками в оснащении). Так при почти равной мощности мотора первый имел в полтора раза меньшую массу и при этом на 75-170 км/ч меньшую скорость (у земли 420км/ч и на высоте 470км/ч), чем более обтекаемы и скоростной, а потому более сложный и более тяжёлый МиГ-3 (у земли 495км/ч, на высоте 640км/ч).
Отношение максимальной скорости МиГ-3 и И-16 и составляет 495/420=1,18.
При этом согласно полученной формуле длина отрывного пузыря пропорциональна квадрату скорости, то есть увеличение скорости на 20% удлинит отрывной пузырь в 1,44 раза.
То есть для такого 20% приращения скорости без срыва потока и проявления Флаттера нужно либо расширить крыло в 1,5 раза, (что, как правило, конструктивно невозможно), либо уменьшить в те же полтора раза радиус скругления носового обтекателя и общую высоту профиля.
Именно таким образом решали проблему разгона МиГ-3, уменьшив толщину крыла по сравнению с И-16, при этом практически не изменив ширину крыла.
Такое снижение несущих балок крыла по высоте в полтора раза да ещё и при увеличении массы самолёта в те же полтора раза неизбежно потребует увеличения сечения наиболее нагруженных горизонтальных полок двутавровых балок приблизительно в 2,5-3 раза, что неизбежно приведет к заметному увеличению массы конструкции крыла в целом.
Сейчас современные дозвуковые аэробусы летают на скоростях 800-900км/ч, при этом не достигая критической скорости Vф, характерной для их профиля крыла. Низкое сопротивление потоку воздуха от тонкого крыла и отсутствие Флаттера на высоких скоростях влечёт за собой малую подъёмную силу при низких скоростях взлёта и посадки, что также требует установки развитой механизации крыла из комплекта закрылков и предкрылков, выдвигаемых из крыла вниз в режимах взлёта и посадки.
Полёт на высоких скоростях без флаттера у современных аэробусов достигается комбинацией технических приёмов, используемых в различных наборах на отдельных участках крыла (см.рис.26-2):
1. Толстая корневая часть имеет большую ширину и максимальную прочность, так что никакие срывы потока и тряска на «воздушных ямах» ей не страшна. На корневой трети крыла закреплён и тяговый двигатель. Именно эта наиболее широкая часть крыла создаёт наибольшую долю подъёмной силы крыла в полёте на крейсерской скорости на высоте 10км. Эта корневая часть имеет установочный угол профиля по отношению к фюзеляжу, равный углу атаки на крейсерской скорости.На корневой части установлены самые мощные выдвижные двухщелевые закрылки и предкрылки.
2. Средняя треть крыл имеет резкое сужение от корневой трапецивидной части. Также эта треть крыла плавно меняет угол атаки от установочного угла корня к нулю на расстоянии 2/3 от фузеляжа. Это изменение угла профиля по длине крыла называют «крутка крыла», что обеспечивает плавное снижение давления на крыле от корня к концу, тем самым снижая негативны эффект от концевого вихреобразования. У средней части такк же имеется механизация из предкрылков и закрылков.
3. Последняя треть крыла наиболее тонкая и не имеет полезной нагрузки при горизонтальном полёте на крейсерской скорости на высоте 10 км. Установочный угол последней трети крыла равен нулю (или близок к нулю). Роль узкой законцовки двойная: а.)Удлинитель крыла для снижения вихреобразовния на второй трети крыла. б) Удлинитель крыла для установки элеронов (рулей крена на крыльях) с максимальным плечём рычага. Установка элеронов исключает установку закрылков на дальнем конце крыла. Предкрылки на последней трети крыла для режимов взлёт-посадки также устанавливают.

Рис.26-2. Схематичный чертёж современного аэробуса, где можно чётко проследить три части крыла: толстую корневую с максимальным установочным углом атаки к фюзеляжу и мощной механизацией из прекрылков и двухщелевых закрылков (основная нагруженная часть в полёте), средняя переходная часть с переменной круткой профиля по углу атаки и полной механизацией из закрылков и предкрылков, крайня часть с нулевым установочным углом атаки и элероном на задней кромке для управления креном самолёта.
Замечательным моментом от проявления флаттера можно считать усиления внимания в СССР к научно-экспериментальному подходу к конструированию в авиации.
Невозможность объяснить на том теоретическом уровне явления флаттера вызвало острую потребность в моделировании полёта новой авиатехники в безопасных лабораторных условиях… В итоге к 1939 году в ЦАГИ была построена крупнейшая в мире на тот момент (вторая на сегодня) ародинамическая труба Т-101. Но ирония в том, что на момент ввода в эксплуатацию Т-101 уже морально устарела, так как её скоростные режимы (максимум 52м/с или 187км/ч) намного отстали от предельных скоростей в авиации на конец 1930-х, да и по размеру самолёты в эти годы уже переросли размеры экспериментальной зоны АДТ. В итоге на этой крупнейшей АДТ можно в реальных условиях испытывать только малоразмерные истребители и спортивные самолёты, да и то только в режимах низкоскоростных взлётов и посадок.
Аэродинамику современных самолётов и режимы течения воздуха вокруг них приходится изучать по отдельным фото самолётов с ярко выражеными туманными шлейфами (см.рис.27).
Добится такого эффекта в натурном виде в АДТ уже практически не возможно.
Данное явление называется Эффект Прандтля — Глоерта — конденсация атмосферной влаги позади объекта, движущегося на околозвуковых скоростях. Эффект чаще всего наблюдается у самолётов, но бывает он заметен и на более низких скоростях даже у автомобилей. Так в условиях очень высокой относительной влажности эффект можно наблюдать и при намного меньших скоростях, например на аэродинамических элементах автомобилей во время гонок Формула-1 в дождливую погоду.
У сверхзвуковых самолётов этот эффект также наблюдается, но при этом демонстрирует совсем иную картину туманных зон разряжения, чётко ограниченных линиями фронтальных ударных волны на лобовых поверхностях крыла и замыкающих волн разрежения при сходе с задней кромки крыла. (см.рис.28)

Рис.27. Полёт современног истрибителя с выпущеной механизацией на больших углах атаки с малой скоростью. Зоны разряжения над крылом выражены интенсивным выпадением тумана, под крылом зоны повышенного давления без образования тумана. Направление движения воздушных потоков под крылом самолёта хорошо отслеживается по туманными шнурами от подвешенных снизу крыла ракет.


Рис.28. Сверхзвуковой полёт с выраженными зонами выпадения тумана от конденсации атмосферной влаги ( Эффект Прандтля — Глоерта). Верхний снимок — при пролёте над переувлажнённым воздухом над морской поверхностью. Нижний снимок- полёт под облаками в условиях влажности близкой к 100%.
Подъёмная сила крыла. Часть № 5.
Подёмная сила крыла при сверхзвуковом полёте
Сверхзвуковой полёт происходит по тем же законам физики и в той же среде, что и дозвуковой полёт, но существенным и крайне значимым различием является нераспространение волн плотности воздуха (звуковых волн) вперёд по ходу сверхзвукового летательного аппарата, что обеспечивает отсутствие влияния возмущённого воздуха из спутного следа на структуру воздушных масс перед крылом летящего самолёта. Это ограничение даёт резкое упрощение в понимании физических процессов взаимодействия крыла с воздухов при сверхзвуковом полёте.
Рассмотрим полёт крыла через идеальный невязкий газ со сверхзвуковой скоростью.
Последуем примеру учебника и рассмотрим взаимодействие идеальной тонкой пластины нулевой толщины с воздухом на сверхзвуковой скорости Мк>1 (Vк>Va).
Угол наклона пластины к скорости примем Ак.
Так как газ идеальный, то есть невязкий, то заторможенный пограничный слой отсутствует и трением между молекулами воздуха по поверхности пластины пренебрегаем.
Тогда летящая пластина с углом Ак к скорости может быть воспринята воздухом как твёрдая поверхность поршня, толкающая воздух перед собой. При этом скорость толкания воздуха в тангенциальном направлении к скорости полёта составит
Vт=Vк*sin Ак.
Так как угол Ак малый, то величина перпендикулярной скорости Vт будет много меньше сверхзвуковой. В таком случае происходит достаточно обычное толкание воздуха пластиной, движущейся с малой постоянной скоростью короткий отрезок времени, равный
Тт=Вк/Vк
Где Вк — ширина пластины в направлении полёта.
Зона влияния этого уплотнения воздуха над пластиной не превышает дальности распространения звуковой волны от каждой точки плпастины за время пролёта пластины Ттi через эту точку неподвижного воздушного пространства. Таким образом, форму этой зоны над пластиной можно ограничить фронтом звуковой волны или конусом распростронения звука в перпендикулярном к скорости Vк направлении за время Тт (конус Маха).
Угол фронта возмущения в воздухе от движения пластины к скорости полёта пластины будет равен
Аа=arctan( Va/Vк)= arctan (1/Мк)
То есть при скорости Vк=Vc наклон фронта волны звукового уплотнения составит 45 градусов.
При этом нам из опытов и шлирен фотографий явно видно, что ударный фронт на скорости 1М перпендикулярен скорости полёта, а на более высоких скоростях отклоняется назад по закону
Аударн= arctan (1/Мк)
То есть угол наклона фронта ударной волны от крыла при 1М будет равен 45 градусов.
При этом скорость удаления фронта звукового возмущения от крыла равна скорости полёта крыла, что описывается следующей геометрической картиной:
Катеты прямоугольного треугольника равны (скорость полёта равна скорости звука перпендикулярно крылу), а гипотенуза- это фронт ударной волны.
При скорости в 2М катеты будут уже иметь отношение 2:1, а угол наклона фронта составит величину
Аударн= arctan (1/2)=26,6 градуса
Такое различие в геометрии ударной волны на лобовых поверхностях и звуковых волн на плоскостях с малыми углами атаки говорит лишь о различии механизмов формирования ударных волн и звуковых волн.
Рассмотрим формирование звуковой волны в перпендикулярном направлении к скорости полёта на малых углах атаки Аа<< Аударн.
Для каждого момента пролёта пластины в данной точке неподвижного воздушного пространства существует своя величина удаления фронта звуковой волны от пластины
Lai=Ттi*Va
А величина поджатия воздуха в элементарном цилиндре с высотой Lai составит
Lтi =Ттi*Vт
В любой момент времен горизонтального полёта для плоской пластины Vт= const
Так как процесс быстротекущий, то воздух в зоне сжатия-разряжения меняет температуру за счёт совершаемой работы на крыле, но не успевает нагреться или остыть при теплообмене со средой, то есть протекает по адиабатическому закону с показателем адиабаты к=1,4 для воздуха
Р/Ро=(Vo/V)^1,4
При таком режиме движения толкающей поверхности у воздуха в зоне сжатия под фронтом звуковой волны появляется уплотнение, величина которого связано постоянным соотношением
Рк= Ро* /(1-Lт/La)^к=Ро/(1-Vт/Vа) ^k= Ро/(1- Vк* sinАк /Vа) ^k =Ро/(1-Мк* sinАк) ^k
Тогда изменение давления будет равно
dPк= Pк-Ро= Ро/(1-Мк* sinАк) ^k — Ро
Величина создаваемого избыточного давления постоянна по всей площади пластины, так как ситуация тождественна во всех соседних сечениях (см рис.29)

Рис.29. Схема продвижения плоской пластины на сверхзвуке через элементарный срез неподвижного воздушного пространства.
Период взаимодействия Тт определяет частоту генерируемой звуковой волны ( период полуволны), а интенсивность волны определяет проекция пластины на перпендикуляр к скорости
Нк=Вк* sinАк.
То есть, чем шире плоскость крыла, тем более низким и глухим будет звук ударной волны. И чем больше угол атаки крыла, тем больше сила звука. Это подтверждается наблюдением, что:
— пули над головой «свистят»- высокий тон 4-5кГц при малой длине самой пули (около2-3см) и короткой длине генерируемой волны ( длина волны 5-8см),
— Широкие лопасти пропеллеров турбовинтовых самолётов «гудят» с частотой около 90-170Гц, более низкий тон из-за значительно большей ширины лопасти ( около 0,5м лопасть и длина волны около 1-2м) в сравнении с размером пули.
Желающие сравнить ощущения от звука на разных частотах могут сами послушать звучание акустического ряда по частоте
yandex.ru/video/preview/?filmId=1603185091132691213&text=частота%20звука&noreask=1&path=wizard&parent-reqid=1583526054883660-1838767931406704632600067-vla1-1828&redircnt=1583526069.1
Итого.
Так как известны жёсткие ограничения по ширине зоны влияния и перпендикулярной к направлению полёта скорости толкающей пластины, то выясняется, что у объёма воздуха внутри конуса сжатия величина сжатия в разных сечениях одинакова.
При этом на плоскую пластину по всей площади давит одинаковое прибавочное давление dP.
Данное рассуждение верно и для пластины с отрицательнным углом –Ак на теневой от потока стороне пластины. Только вместо избыточного давления на ней будет разряжение на величину dP.
Простейший расчёт для плоского крыла на сверхзвуковой скорости Мк=1 даёт подъёмную силу на каждую сторону поверхности (давление) на уровне моря более 150кг/м.кв на каждый 1 процент уклона плоскости (100%*Нк/Вк), или более 300кг/м.кв при суммировании двух сторон идеально плоского тонкого крыла.
То есть уже при величине уклона крыла 2% (или 1,2 градуса угла атаки) обеспечивается необходимая современному истребителю удельная подъёмная сила на крыло в размере 500-600кг/м.кв при давлении атмосферы на уровне моря.
Для обеспечения манёвра с перегрузкойи в 10g в плотных нижних слоях атмосферы достаточно угла атаки на сверхзвуке 1,1М всего в 6,5 или 9 градусов (для Су- 57 и Су-35 соответственно).
А вот в разреженных слоях атмосферы уже на высоте 10км такие запредельные перегрузки становятся практически не реализуемы, так как для торможения с ускорением 10g пришлось бы практичеси ставит весь самолёт перпендикулярно потоку.
На больших высотах плотность воздуха и давление соответственно падают, что требует кратно больших углов атаки при той же сверхзвуковой скорости, или требует резкого роста скорости для компенсации падения давления воздуха в атмосфере и сохранения приемлемых углов атаки.
Именно с этим связанны столь высокие скорости истребителей (до 2,5Мах) на высотах 25км, где давление воздуха падает до 2,5% от величины на поверхности моря. И даже на таких скоростях углы атаки в разреженном воздухе приходится поднимать до критических 10-12градусов.
Данные расчёт можно проверить на примере сравнения двух практически одинаковых по большинству параметров самолётов Су-35 и Су-57. Они почти совпадают по массе, габаритам и тяге двигателей. Из массо- габаритных характеристик у них отличаются только площадь крыла и, как следствие, максимальная удельная нагрузка на крыло (см.Таб. Бис.30)

Рис.30 Таблица сравнения технических характеристик самолётов Су-57 и Су-35. Жёлтым указан сильно различающийся параметр в геометрии самолётов, а зелёным указаны последствия в изменениях ТТХ от модели к модели.
Результатом такого различия по удельной нагрузке на крыло оказывается увеличение: Максимальной скорости на сверхзвуке, максимальной высоты полёта, максимальной сверхзвуковой скорости без форсажа и максимально дальности полёта.
Попробуем получить эти выигрыши из полученых расчётных зависимостей подъёмной силы плоского крыла. Ниже приведены результаты расчётов в таблице, где попарно рассматривается на одном эшелоне с одинаковой скоростью самолёты Су-57 и Су-35.
Интересно отметить, что с ростом высоты полёта роль разряжения над крылом снижается, а роль сжатия становится доминирующей, достигая более 80% подъёмной силы на максимальной высоте полёта (см. рис.31. столбцы с показателями dP над и под крылом). Тогда как на уровне земли разряжение и сжатие вносят практически одинаковый вклад в создание подъёмной силы крыла на сверхзвуке.

Рис.31. Таблица сравнения аэродинамических характеристик самолётов Су-57 и Су-35. Внизу дополнительно указана строчка с характеристикой полёта американского самолёта разведчика «Чёрный дрозд» SR-71на скорости 3,2М на высоте 25 км.
Внизу таблицы отдельной строчкой показан пример максимальных полётных характеристик американского самолёта разведчика «Чёрный дрозд» SR-71, который по компоновке ближе к Су-57, а взлётные нагрузки на крыло ближе к СУ-35. Особенностью SR-71 является масса топлива на борту, составляющая 60% при влёте, тогда как у наших истребителей взлётный запас топлива всего 30% от максимальной взлётной массы. Таким образом, за время полёта нагрузка на крыло SR-71 изменяется от состояния хуже Су-35 в начале и до лучше Су-57 в конце полёта.
Интересно как отразилось на экстерьере истребителя Су-57 увеличение площади крыла на 32%.
Так если Су-35 выглядит эффектным самолётом с выраженным делением на крылья с явно отеделённым хвостовым оперением и агрессивным клювом наклонного к плоскости крыла фюзеляжем с кабиной экипажа, то облик Су-57 выглядит скучным плоским летающим блюдцем со слившимися в единый диск крыльями и хвостовым оперением. Су-57 эффектно выглядядит только в виде с верху, тогда как Су-35 выглядит крайне эффектно с любого ракурса (см. рис.32 -35)


Рис.32. Сравнение экстерьеров Су-35 (вверху) и Су-57(внизу). Заметно сильное уплощение Су-57 в профильной проекции, в сравнение с «крючконосым» Су-35.


Фото. 33. Сравнение вида Су-35 (вверху) и Су-57(внизу) в полёте. Явно выраженный наклон вниз передней части фюзеляжа у Су-35 говорит о больших углах атаки крыла в большую часть времени полёта, чтобы в этом положении фюзеляж находился горизонтально к скорости, тем самым минимизируя сопротивление полёту. У Су-57 фюзеляж вообще не выражен, при этом носовая его часть с кабиной является продолжением корневых наплывов крыла. То есть в борьбе за высокую сверхзвуковую скорость без форсажа лобовая проекция самолёта была минимизирована так, что фюзеляж редуцировался до утолщения крыла в корневой его части.


Рис.34. Сравнение экстерьеров «Чёрный дрозд» RS-71 и Су-57(внизу). Заметно сильное внешнее сходство этих очень разных самолётов в борьбе за высокую сверхзвуковую скорость в длительном режиме.


Рис.35. Внешний вид сверзвукового высотного самолёта-разведчика США «Чёрный дрозд» RS-71
Пластина с изломом на сверхзвуковой скорости.
Случай с ломаной пластиной характерен для тонкого участка лобовой кромки крыла, которую по конструктивным причинам невозможно сделать абсолютно тонкой и абсолютно острой, что приводит к появлению технически исполнимого достаточно большого по величине угла на лобовом обтекателе или на подвижном предкрылке. Местный угол профиля на предкрылке может быть в разы больше общей относительной толщины крыла. При общей относительной толщине крыла у современного истребителя около 5% (150мм при ширине крыла 3м), то на предкрылке шириной в 500мм и толщиной в корне в те же 150мм относительная высота элемента составит уже 150/500=30% (16 градусов)
Именно на этом клине возникает столь характерная для сверзвукового полёта ударная зона с формированием узко направленой ударной волны вдоль границы конуса маха.
Формирование волны высокой плотности от клинового обтекателя в границах конуса Маха создаёт интенсивное разряжение над крылом внутри конуса Маха, когда расширение профиля к середине крыла переходит в обратный уклон к задней кромке крыла.
Именно эту зону резкого разряжения и адиабатного охлаждения над крылом внутри конуса Маха видно на фотографиях, где образуется клиновидное конденсационно-туманное облако над обеими сторонами крыла, летящего на сверхзвуке самолёта. (см.рис 28).
Согласно расчёту ( см таб.рис.31) на малой высоте у земли в плотных слоях атмосферы полёт на сверхзвуке идёт на сверхмалых углах атаки (менее одного градуса), что обеспечивает зоны отрицательных углов и сильного разряжения (как следствия) на задней кромке крыла с обеих сторон крыла. Именно эти малые углы атаки обеспечивают визуальную симметрию туманных конусов за истребителями на фотографиях, снятых с земли.
Распределение ударных волн от обтекателя по сторонам крыла можно регулировать изменением отклонения предкрылка, смещая атакующий угол в одну из сторон.
Таким образом, можно создать подъёмную силу на плоском крыле даже при нулевом угле атаки, управляя лишь степенью асимметрии расположения клиновидного лобового обтекателя к встречному потоку. При этом на лобовом обтекателе с большим углом наклона к потоку возникает значительная подъёмная сила.
Теоретически можно добиться одностороннего выпадения тумана в конусе Маха даже на сверхзвуке, но при этом придётся разгрузить одну из плоскостей крыла, сделав её абсолютно плоской и горизонтальной в полёте. При этом на острый предкрылок сваливается избыточная нагрузка от веса самолёта, что перегружает отклоняемый клиновидный предкрылок, предъявляя излишне высокие прочностные требования к этому сравнительно небольшому элементу крыла. Поэтому на сверхзвуке предкрылок выставляют в основном в нейтральное положение к скорости, давая равномерную распределённую нагрузку по всей площади крыла с обеих сторон.
В итоге формируется суммарная подъёмная сила крыла, состоящая из нескольких частей, количественно равное числу граней на плоскостях сверхзвукового крыла, включающие в себя и отклоняемые элементы предкрылков и закрылков.
Срыв потока с задней кромки крыла и формирование «волн расширения-сжатия» на шлирен-фотографиях
В момент окончания прохода крыла через неподвижный воздух за его задней кромкой происходит резкое исчезновение воздействия крыла на окружающий воздух. Сжатое состояние под крылом сменяется состоянием разряжения в спутной струе, а смещённые массы воздуха начинают возвращатся назад под действием давления окружающей атмосферы. При этом разряжение над крылом резко встречается с зоной избыточного давления под крылом. На границе напряжённого объёма в конусе Маха и релаксантного участка в спутной струе возникает узкая граница резкого изменения плотности воздуха от избыточного давления к разряжению (и на оборот с другой стороны крыла). Именно эта линейная граница разных плотностей воздуха ярко проявляется на снимках в шлирен-освещении резкой оптической неоднородностью. При этом сама по себе тёмная линия на шлирен-изображении не даёт возможности понять разряжение в ней или сжатие, или это граница различных плотностей воздуха по разные стороны от неё. (см.рис. 36-37)

Рис. 36. Фото оптических неоднородностей, вызванных пролётом пули на разных скоростях. Левая- 700-800м/с, средняя- около 400м/с, правая- менее 330м/с (нет ударного фрона на острие, то есть уже дозвуковой полёт). О скорости пули свидетельствуют угол отклонения тонкой линии ударной волны от острия пули.

Рис. 37. Фото оптических неоднородностей (ударных фронтов), вызванных пролётом пули на скорости около 700-800м/с.
Последний снимок (рис.37) особенно интересен появлением заметного ударного фронта от тонкой кольцевой канавки в задней половине пули. То есть локальное незначительное изменение на практически параллельной к скорости поверхности пули вызывает появление выраженного ударного фронта, простирающемся на значительное удаление в пространстве и времени.
Фактически данный поясок создаёт маленькое высокочастотное шумовое включение в основное низкочастотное возмущение от пролёта пули. Тем самым эта фотография подтверждает и так известный из «Акустики» факт, что слышимые нами звуки формируются последовтельностью чередований фронтов плотности воздуха различной величиной давления в них и с различной шириной (длиной волны). Последовательно пущенные волны так и следуют друг за другом без смешивания, неся информацию о колебательных характеристиках источника звуковой волны.
Также на снимке (рис.37) интересно то, что сход потока с донного среза пули вообще не вызывает никакого заметного глазом оптического следа, а ударная волна присоединения возникает много дальше за концом пули на удалённом участке сжимающейся спутной струи.
То есть при мягком по кривезне сходе потока с твёрдого тела на спутный след возможна ситуация, когда спутный след становится как бы нейтральным продолжением твёрдого тела (т.н.«фиктивное тело»).
А возникающие линии ударных волн при соприкасновении потоков позади тела обозначают границу этого «фиктивного тела», тогда как в учебниках эти линии расширения-сжатия рисуют строго на задней кромке крыла в случае изображения сверхзвукового полёты крыла.
Подъёмная сила крыла. Часть № 6.
Подъёмная сила крыльев биплана и полипланных схем самолётов.
Монин Илья Алексеевич, к.т.н.МГТУ им.Баумана., imoninpgd@gmail.com
Прошёл ещё год с момента публикации последних частей этой статьи (сейчас 10 июля 2021).
В итоге за два с половиной года с февраля 2019 года статья набрала более 64 тыс. просмотров (из них 23 тыс. просмотров за последние полтора года), что показывает неослабевающий интерес людей к этой достаточно плохо объяснённой в физике теме.
Желающих поделится впечатлениями или замечаниями прошу обращаться по электронной почте: imoninpgd@gmail.com
Ответов на сайте ХАБР давать не могу, так как лишён возможности отвечать из- за глубоких минус 50 в карме.
Зачем продолжать изучение аэродинамики крыла, если самолёты и так прекрасно летают?
При создании каждой новой версии для привычных и общеизвестных теорий нужно ответить на один важный вопрос: Что нового может дать эта новая версия теории?
Для модели явления «подъёмной силы крыла» за счёт отклонения потока воздуха таким новым качеством является теоретический расчёт подъёмной силы для крыльев в виде тонких радиусно изогнутых пластин, для которых привычная теория по Бернулли не давала вразумительного ответа.
Интересным выводом из новой модели является то, что возможен прямой переход от теоретического расчёта к эмпирической формуле, получаемой экспериментально.
На сегодня при продувке макета крыла в АДТ экспериментально получают значение
Fкр=V^2* q*S*Cy/2
Где V- cкорость горизонтального полёта крыла сквозь воздушное пространство, q- плотность воздуха, Су- экспериментальны коэффициент для расчёта вертикальной составляющее от силы сопротивления потоку воздуха.
При этом крайне важно наличие множителя «2» в знаменателе, так как её вносят просто как множитель в величине скоростного напора Pv= V^2*q/2
При этом конкретное Cy и Cx для конкретного крыла на конкретном режиме продувки вбирают в себя все неучтённые нюансы аэродинамики обтекания конкретного крыла потоком воздуха, выдавая в конце вполне закономерный правильный экспериментальный результат.
В случае радиусного тонкого крыла мы можем рассчитать величины Сх и Су прямо из геометрии крыла, после чего сравнить результат и сделать некие интересные и далеко идущие выводы.
Так для радиусно изогнутой пластин можно рассчитать давление на крыло по формуле
Р= V^2* q*dh/R
Где dh- толщина отклоняемого крылом слоя воздуха, R- радиус кривизны отклоняемого слоя воздуха.
Исходя из ранее проведённых расчётов (см. часть 1) известно, что качество крыла Ккр= В/Н, то есть связано только с геометрией изогнутой пластины.
Достроим к изогнутой пластине действующие радиусы кривизны у её концов, в результате чего получаем равнобедренный треугольник ABD с высотой DE. (см.рис.1)
При этом из условия подобия треугольников ABC и ADE можно вычислит значение для радиуса кривизны R.
Так треугольники ABC и ADE подобны по критерию равенства двух углов у основания (один угол <CAB общий для обоих треугольников, а другой угол прямой у каждого треугольника отдельно).

Рис.1. Геометрия треугольника на хорде радиусного крыла для расчёта радиуса кривизны.
При этом, согласно подобию, стороны треугольников соотносятся как
R/(0,5*В)=В/H
Откуда получаем R=0,5*В^2/ Н
Так как в нашей модели радиусного крыла Ккр=Н/В,
То подставляя выражение Ккр в выражение для R получаем:
R=0,5*В^2/ Н= 0,5*В*(В/Н)= 0,5*В *Ккр
Итого: R=0,5*В*Ккр
Теперь полученное выражение для R можно подставить в выражение для давления на крыло, и в результате получаем:
Р= V^2* q*dh/R= V^2* q*dh/ (0,5*В*Ккр)=V^2* q*dh*2/ (В*Ккр)
Итого: Р= V^2* q*dh*2/ (В*Ккр)
Мы получили формулу связи давления на крыло с шириной крыла В (легко замеряемой линейкой) и безразмерным коэффициентом Ккр (однозначно получаемым для профиля при продувках в АДТ).
Теперь для получения величины подъёмной силы Fкр на крыле нам достаточно площадь крыла Sкр=B*L умножить на величину давления на крыло Р, и получаем:
Fкр=Sкр*Р= B*L* V^2* q*dh*2/ (В*Ккр)
Сокращаем однородные члены «В» в числителе и знаменателе и получаем:
Fкр= L* V^2* q*dh*2/ Ккр
Формула совершенно нетривиальная, так как оказалось, что подъёмная сила крыла с известным качеством Ккр зависит только от длины крыла L и зоны влияния по толщине поджимаемого слоя dh, но не зависит от ширины крыла В.
При этом в числителе появился множитель «2», а вовсе не в знаменателе, как это принято писать в выражении скоростного напора.
Теперь приравняем традиционное выражение подъёмной силы крыла с экспериментальным коэффициентом «Cу» к выведенном нами выражению для тонкой радиусной пластины:
Fкр=V^2* q*S*Cy/2
Fкр= L* V^2* q*dh*2/ Ккр
Приравняв правые стороны двух выражений, получаем:
V^2* q*S*Cy/2= L* V^2* q*dh*2/ Ккр
Сокращаем однородные члены:
S*Cy/2= L* dh*2/ Ккр
Раскладываем площадь S прямоугольного в плане крыла как S=B*L и подставляем в выражение:
B*L *Cy/2= L*dh*2/ Ккр
Снова сокращаем однородные члены и получаем:
B*Cy/2= dh*2/ Ккр
В этом выражении неизвестен только один параметр, а именно зона влияния dh. Вот его мы и выразим:
dh= (B*Cy/2)/ (2/ Ккр)= (B*Cy/2)*(Ккр/2)= B*Cy*Ккр/4
Итого: dh= B*Cy*Ккр/4
Данное выражение удивительным образом позволяет определить расчётом условную зону деформированного слоя воздуха вокруг крыла из его собственной геометрии и вполне легко замеряемых в АДТ силовых параметров на крыле.
Можем рассмотреть значение параметра «dh» на параметрах от продувки эталонных профилей в АДТ.


Рис.2. Профиль А-9% из справочника и его характеристики Су и Сх с продувки в АДТ.

Рис.3. Профиль А-18% из справочника и его характеристики Су и Сх с продувки в АДТ.
Рассмотрим профиль А-18% и сравним с А-9%
Для толстого профиля на углах 4 градуса Ккр=18 при этом Су=0,486, что даёт нам расчётный dh=В*0,486*18/4=2,187*В.
Для угла 18 градусов Ккр=7,47 при этом Су=1,23, что даёт нам расчётный dh=В*1,23*7,47 /4=2,3*В
На промежуточных углах атаки 8-12 градусов величина влияния возрастает до более чем dh=3*В. (см.таб.рис.4)

Рис. 4. Таблица экспериментальных и производных аэродинамических характеристик профиля типа А с относительной толщиной 18%.
Таким образом, как для режима полёта с наибольшим качеством крыла (крейсерская скорость), так и для посадочного режима (минимальный Ккр при максимальном Су) зона влияния «dh» имеет толщину более двух хорд крыла.
Это расчёт достаточно ярко показывает, что нужно делать для реализации бипланной схемы самолёта с максимальной эффективностью.
При этом мы брали толстый профиль с относительной толщиной 18%, более характерный для тихоходной авиации первой трети 20-го века.
Если взять профиль для более скоростных самолётов с относительной толщиной 9%, то принципиально картина не изменится.

Рис. 5 Выборочная таблица аэродинамических характеристик профиля типа А-9%.
Для угла 4 градуса Ккр=25,7 при этом Су=0,396, что даёт нам расчётный dh=В*0,486*18/4=2,545*В.
Для угла 16 градуса Ккр=7,39 при этом Су=1,08, что даёт нам расчётный dh=В*1,08*7,39 /4=1,997*В
Таким образом, из всего сказанного можно сделать вывод, что для создания эффективного биплана нужно делать большое расстояние между крыльями, а именно более 2,5 хорд крыла. Только при этом взаимном положении взаимное влияние крыльев в полёте будет минимизировано.
В противном случае, при более близком положении ярусов крыльев, взаимное влияние значительно снизит общую подъёмную силу системы крыльев.
Из этого заключения можно сделать интересный вывод про эффективность аэродинамической схемы самолёта-биплана АН-2.

Рис.6. Вид биплана Ан-2, чертёж в трёх проекциях.
Так хорошо видно, что расстояние между ярусами крыльев заметно меньше хорды крыла. То есть у биплана Ан-2 присутствует сильное взаимное влияние параллельно расположенных крыльев, чем резко уменьшается их суммарная подъёмная сила.
Из экспериментальных исследований в АДТ известно, что для биплана Ан-2 прибавка подъёмной силы составляет всего около +20%, чем если бы самолёт имел только одно монопланное верхнее крыло того же размера (то есть при почти в два раза меньшей площади крыльев).
По сути, самолёт сделан бипланом только ради создания крупноформатной несущей фермы, где высота фермы почти равна хорде крыла. При этом горизонтальные балки из двух рядов крыльев распирались одной жёсткой и прочной распорной стойкой между крыльями, а также стягивались тонкими диагональными растяжками из стальных тросов.
Такое решение позволяло сделать более прочное и относительно лёгкое крыло для тяжёлого самолёта из не очень прочных и не самых лёгких материалов, доступных для гражданской авиации на момент создания АН-2.Таким образом, выигрыш по массе и стоимости самолёта был достигнут в ущерб максимальной скорости и топливной экономичности полёта.

Рис.7. Поляра самолёт Ан-2 в целом на различных режимах выпущенной механизации крыла.

Рис.8. Табличная форма для поляр самолёт Ан-2 в целом на различных режимах полёта с гладким крылом и выпущенной механизацией крыла с расчётом дополнительных параметров. Цветом выделены предельные режимы полёта (крейсерский и посадочный режим).
Максимальное качество самолёта Ан-2 в целом находится в районе К=11,2 на крейсерской скорости, а в посадочном режиме около К=4,5.
При этом на больших углах атаки Ан-2 показывает К=4,5 как на гладком крыле, так и с с выпущенной механизацией крыла (предкрылки + закрылки).
Вот только с выпущенной механизацией возникает совершенно запредельны Су=1,966, позволяющий садится на скорости 91км/ч с полной массой 5500кг. (см. рис.7-8.таб.)
И этот коэффициент отнесён к суммарной площади двух крыльев, что при их неравномерной загрузке обеспечивает для отдельных частей крыльев Су = 3...4
Такой удивительно большой Су=2 требует какого-то объяснения, так как ближайший по характеристикам толстый профиль из справочника не даёт столь высокого показателя при достаточно вменяемом Ксам=4,5.
Ниже приведён профиль с максимальным Су из справочника.

Рис.9. Профиль Р-III (15,5%) из справочника и его характеристики Су и Сх с продувки в АДТ.
Профиль вообще выглядит малообтекаемым, с крутолобым передним краем и максимум толщины на 0,2 хорды.
При этом профиль имеет достаточно высокий К=17,5 на угле атаки 4 град, при одновременно высоком Су=0,56.
Так что не случайно данный профиль был применён на множестве различных планеров в 1930-х годах в СССР.
Кстати, и у Ан-2 профиль крыла очень похож на Р-III (15,5%), (см. фото. рис.10).
И совсем похожим на Р-III (15,5%) профиль крыла у Ан-2 становится при сдвинутом вперёд и вниз предкрылком. (см. рис.11).

Рис.10. Профиль крыла самолёта Ан-2 в реальном срезе (фото).

Рис.11. Профиль крыла самолёта Ан-2 в чертеже.
Современные прототипы для замены АН-2 делаются уже по монопланной схеме (самолёты: «Байкал» — ЛМС-901, «Грач» Т-101).(см.рис.12-13)
Так сейчас прочность современных композиционных материалов уже позволяет обеспечить нужную прочность крыла при допустимом его весе в чистом монопланном исполнении (или только с дополнительными подкосами, без полноценного толстого нижнего крыла).
То есть по сути нижнее крыло для АН-2 требовалось только как прочная балка пространственной фермы, а в аэродинамическом качестве оно больше мешало, чем помогало.

Рис.12. Экспериментальный ремоторизованный моноплан «Грач» Т-101 на базе планера АН-2, построен на Московском авиационном производственном объединении (МАПО) в конце 1993г.

Рис. 13. Перспективный композитный самолёт «Байкал» — ЛМС-901
В итоге монопланный «Байкал» — ЛМС-901, как заместитель для АН-2, оказывается по всем лётными качествами значительно лучшими самолётом, чем старик Ан-2.

Рис.14. Таблица сравнения характеристик самолёта Ан-2 и его современных «заместителей».
Так ЛМС-901 оказался в полтора раза быстрее на крейсерской скорости, чем АН-2.
При этом ЛМС-901, при большей грузоподъёмности и большей дальности полёта, имеет почти на 1500 кг меньший сухой вес при меньшем размахе крыльев и в два раза меньшей площади крыла, чем у АН-2.
И только по посадочной скорости моноплан проигрывает биплану, что как раз и связано с аномально высоким Су крыльевой системы биплана.
Учитывая полученные новые знания об аэродинамике во взаимном влиянии крыльев в бипланной схеме, можно предложить схему биплана, который в размерности и габаритах АН-2 будет летать быстрее и экономичнее.
Для этого достаточно разнести крылья на большую высоту друг от друга и укоротить их по длине в полтора раза. Правда, самолёт такой конфигурации больше напоминает воздушный змей, чем нормальный привычный самолёт.
Суммарная длина двух крыльев эффективного биплана будет составлять 120% от длины одного верхнего крыла АН-2. (см.рис. 15 )
Также можно попытаться создать триплан с более узкими крыльями (см.рис. 16 ).
Уменьшение хорды в 2 раза снижает удельную грузоподъёмность крыла (на погонный метр) в те же два раза, так что триплан с зауженным крылом придётся строить с размахом крыла почти как у АН-2, что нецелесообразно.

Рис.15. Эквивалентная АН-2 конструкция биплана с разнесением крыльев за пределы их зон аэродинамического взаимного влияния.


Рис. 16. Схема триплана на базе Ан-2 с зауженными в два раза крыльями для снижения высоты зон аэродинамического влияния и уменьшения расстояния между крыльями.
В начале 1920-х были популярны полипланные схемы, что отразилось в появлении натурных образцов и трипланов. Но из-за непонимания сути явления «подъёмной силы крыла» и недоучёта взаимного влияния крыльев триплан показал крайнюю неэффективность даже в сравнении с бипланом. Пример такого самолёта является КОМТА, созданный под непосредственным руководством Н.Е.Жуковского, профессора в области аэродинамики.

Рис. 17. Чертёж в трёх проекциях триплана КОМТА образца 1923г. (автор Жуковский Н.Е.)
Если бы Жуковский просто приказал выломать среднее крыло из конструкции своего триплана, оставив его силовой каркас, то самолёт сразу полетел бы гораздо лучше. Но «мэтр» жил в своём иллюзорном мире заблуждений об аэродинамике, и такая яркая неудача в прикладном конструировании самолёта не смогла его ничему научить.
Тем не менее, не смотря на общий негативный результат применения полипланной схемы в конструировании самолётов, был один удивительный пример аж семиплана с 7-ю параллельными рядами узких крыльев с большим расстоянием между ними (см.рис.18-19). Появился он в США в 1923 году, тогда же когда и неудачный триплан Жуковского в России. Его построил американский инженер Фредерик Герхардт (W. FrederickGerhardt), сотрудник Мичиганского университета.
Этот самолёт-семиплан умудрился взлететь даже на мускульной тяге, то есть двигателем был сам человек, крутивший велосипедные педали внутри корпуса!!!
И хотя полёт был всего на несколько метров в длину и на 0,6 метра ввысоту, но сам отрыв от земли этого типа ультралёгких самолётов является большим успехом.
До попытки самостоятельного взлёта на педалях данный семиплан уже вполне успешно взлетал на буксире за автомобилем (как воздушный змей), после чего автор решился на самостоятельны взлёт. Но вот недостаток мощности человеческих ног автор семиплана недооценил.
С тех пор мало кто возвращался к полипланной схеме в мускулолётах, хотя именно в этом классе мультплан имеет значительный преимущества в сравнении с монопланом с единым толстым крылом.
При наличии современных прочных материалов вполне можно повторить рекордный семиплан на новом качественном уровне, уже понимая суть проблемы полипланных крыльев. Хотя на воздушных привязных змеях, дельтапланах, парапланах и парашютах люди и так уже давно летают, что по сути очень близко к данному мультиплану.

Рис. 18. Фото семиплана-мускулолёта образца 1923г. (автор Фредерик Герхардт (W. FrederickGerhardt), сотрудник Мичиганского университета.)

Рис.19. Фото семиплана-мускулолёта образца 1923г. за мгновение до взлёта и крушения. Крылья хилой конструкции сложились при попытке взлёта сразу после отрыва самолёта от земли, не выдержав значительной нагрузки от подъёмной силы крыльев.
В современном мире полипланные крылья используются в ограниченной области ультра-высоких сверхзвуковых скоростей в качестве аэродинамических рулей ( сверхзвуковые ракеты и баллистические сверхзвуковые снаряды). При этом полипланные рули выглядит как решётка с квадратными ячейками, а ширина планок решётки равна размеру ячейки в плане. (см.фото. рис.20-26)

Рис.20. Фото решётчатых аэродинамических рулей (полипланных) у ракеты на подвеске крыла боевого самолёта.

Рис.21. Фото решётчатых аэродинамических рулей у разгонного блока боевой ракеты.

Рис.22. Фото решётчатых аэродинамических рулей у гражданской ракеты-носителя Фалькон 9 (США).

Рис.23. Фото решётчатых аэродинамических рулей у гражданской ракеты-носителя СОЮЗ (Россия).

Рис.24. Фото в цеху: на стенде решётчатый аэродинамический руль от гражданской ракеты-носителя Фалькон 9 (США).

Рис.25. Фото решётчатых аэродинамических рулей на гражданской ракете-носителе Фалькон 9 (США) в сравнении с людьми.
При продувке такого аэродинамического полипланного решетчатого крыла в АДТ на дозвуковой скорости был получен весьма низкий Ккр=2,5, что объясняется значительным взаимным влиянием близко расположенных параллельных крыльев и большим паразитным сопротивлением перпендикулярных распорок с частым шагом. Но на кратных сверхзвуковых скоростях у такого решётчатого руля недостатки обращаются в достоинства, так как взаимное влияние плоскостей в решётке резко снижается. Так зона влияния крыльев на сверхзвуке рассчитывается уже по углу конуса Маха, что означает ширину влияния в каждую сторону не больше ширины хорды крыла деленной на число Маха М:
Сверхзвуковой dh= B/M
К полипланным схемам крыла также можно отнести современный планирующий парашют типа «летающее крыло», только с нулевым расстоянием между крыльями (нет щели сзади между плоскостями). Кстати у парашюта-крыла тоже низкое качество крыла Ккр=2,5, то есть такое же, как и у решетчатых рулей.
Низкое качество крыла тряпочных крыльев-змеев не позволяет применять их для мускулолётов.
Так энергетическая оценка «тягового двигателя» для парашюта при Ккр=2,5 даёт мощность около 5 кВт: для парашютиста с парашютом общей массой 100кг и вертикально скоростью снижения Vверт=5м/с (приемлемая посадочная вертикальная скорость) мощность тяги от сил тяжести по вертикали (она же и для для горизонтального полёта при пассивном планировании) составит около N=100кг*9,81*5= 5кВт, что никак не вписывается в возможности мускулолётов.
При поступательной скорости Vгор=Ккр*Vверт=2,5*5= 12,5м/с (45км/ч) полёт и приземление без защитной кабины и колёсного шасси становится уже достаточно опасным действием, а потому без манёвра резкого торможения перед посадкой парашютисты не приземляются.
У парашюта-крыла есть верхняя плоскость, нижняя плоскость и зазор между ними с вертикальными стойками-мембранами.
По фотографии парашюта в полёте видно, что давление внутри купола выше атмосферного, что видно по выпуклой форме натянутой ткани, как на верхней, так и на нижней поверхности купола. Общая выпуклость парашюта-крыла говорит, что давление внутри купола выше, чем избыточное давления от набегающего снизу потока воздуха.
Таким образом, при известной массе человка с парашютом и известной площадью купола можно оценить создаваемые куполом удельные Су и Сх при планирующем полёте. При площади спортивного купола-крыла 12м.кв и массе человека с амуницией 80кг получаем нагрузку около Fy=7кг/м.кв (70Па).
Скоростной напор по горизонтали на скорости 45км/ч (12,5м/с) составит:
Рv= (12,5)^2*1,2/2=94Па
Тогда для крыла получим параметр Су:
Су = Fy/Pv =70/94= 0,74
Что при К кр=2,5 даёт Сх= Cy/Ккр = 0,74/2,5 = 0,3
Однозначно можно сказать, что купол парашюта-крыла надут избыточным давлением равным скоростному напору от поступательной скорости его полёта. То есть внутри купола воздух почти не движется или движется много медленнее, чем скорость полёта (небольшой расход воздуха вбок за счёт просачивания сквозь ткань), ведь у современных куполов вообще нет выходных отверстий на задней кромке крыла. (см.рис.26-27)
У круглых парашютов типа Д6 с площадью купола 80м.кв при массе человека с амуницией 140кг получаем нагрузку около Fy=140/80=1,75кг/м.кв (17,5Па).
При этом при скоростью спуска 5м/с скоростной напор:
Рv=5^2*1,2/2=15Па
В итоге можем получить коэффициент лобового сопротивления тела сложной формы ( чаши купола кромками на поток с щелями по бокам) (см.фото.рис.28), что даёт нам Сd круглого парашюта:
Сd = Fy/Pv =17,5/15= 1,17
Такой Сd прекрасно соответствует справочным значениям для тел вращения (см.главу 2-3)

Рис.26. Фото парашюта типа «Крыло», вид спереди на воздухозаборы купола.

Рис.27. Фото парашюта типа «Крыло», вид сзади на отсутствие выхода воздуха сзади купола.

Рис.28. Фото круглого десантного парашюта, с щелями в куполе для создания горизонтального ускорения полёта.
Куда же девается воздух с пути купола парашюта, который не смог протиснутся сквозь протоки купола?
Почти весь воздух отклоняется от летящего купола, воспринимая его как единое твёрдое тело. Таким образом, купол крыла можно рассматривать как твёрдое крыло гигантского размера, летящего по воздуху с балансировкой и управлением за счёт изменения положения подвешенного снизу крыла груза (парашютиста). Аналогичную гравитационную балансировку применяют на дельтапланах (см.рис.29) и на сверхлёгком сверхвысотном беспилотном самолёте NASA Helios.(cм.рис.30)

Рис.29. Фото дельтаплана. Управление углом атаки и креном крыла дельтаплана осуществляется отклонением центра масс подвешенного пилота по отношению к крылу.

Рис.30. Фото сверхлёгкого сверхвысотного беспилотного самолёте NASA Helios, ширина крыла более 2,5м., размах крыла более 70м. Управление углом атаки крыла осуществляется отклонением центра масс подвешенных снизу крыла опор шасси по отношению к крылу.
Похожее явление запирания потока воздуха (как у купола парашюта-крыла) происходит между крыльями биплана.
Так сильно опущенный вниз закрылок верхнего крыла заужает проход для воздуха, таким образом, верхнее крыло как бы утолщается на величину отгиба закрылка. (см.рис.31)
То есть отклоняя закрылок верхнего крыла удаётся преобразовать аэродинамику верхнего крыла биплана в подобие гигантских толстых крыльев тихоходных самолётов – гигантов конца 1920-х начала 1930-х годов. (см.часть №2 этой статьи)
На малых скоростях полёта бипланов сжатие потока за счёт давления скоростного потока крайне мало и почти не обнаружимо на глаз. Так при взлёт-посадочных скоростях 90км/ч (25м/с) у Ан-2 скоростной напор всего 375 Па, что с учётом базового атмосферного давления 100кПа даст поджатие потока всего на 0, 375% по толщине слоя воздуха (3,75мм на 1 метр слоя).
Поэтому воздух не способен протискиваться в узкие щели на повышенной скорости при столь малых избыточных давлениях, а потому вынужден обходить дальней стороной такие сужающиеся щели между плоскостями.
Невозможность равномерно течь по всей ширине зазора между крыльями вызывает образование застойных зон постоянного давления в неудобных для протекания потока местах.
Критерием «удобного» маршрута прохода потока является соблюдение двух условий:
— максимальная постоянна ширина потока (максимальный расход при постоянной скорости);
— минимальна кривизна потока (максимальный радиус кривизны дуги).
Эти два критерия дают минимальное сопротивление прохождения воздуха через препятствие.
Исходя из этого критерия можно построить приблизительную картину протекания воздуха между крыльями в посадочном режиме на больших углах атаки с выпущенной механизацией крыла.
Распределение давления между крыльями биплана в посадочном режиме с полностью выдвинутой механизацией крыла видно на рисунке, моделирующем протекание воздуха (см.рис.31)

Рис.31. Схема воздушных потоков вокруг крыльев при посадке Ан-2 на углах атаки 16град при полностью выпущенной механизации крыльев (предкрылки + закрылки), и возникающие при этом застойные зоны с постоянным давлением.
В направленных на набегающий поток зонах в лобовой части крыльев возникает давление
dP1= Pvo.
То есть на лобовых обтекателях в застойных зонах давление одинаково и равно скоростному напору от скорости полёта Vo.
Давление в тени крыльев уже связано с режимом обтекания отрывной струи над конкретной застойной зоной.
Малая зона под нижним крылом с dP3 может иметь как положительное, так и отрицательное значение. Также dP3 может быть равным с dP4, если отрывной поток не касается отогнутого вниз закрылка, оставляя всю нижнюю плоскость в объёме большой нижней застойной зоны.
Разрежение dP2 больше (абсолютное давление меньше), чем у dP4, что и объясняет загиб сквозного потока вверх (выпуклость в сторону большего давления, то есть вниз) после выхода из зазора между крыльев.
Из данного распределения давления следует, что нижнее крыло может создавать небольшую отрицательную или положительную подъёмную силу, а верхнее крыло создаёт очень большую положительную подъёмную силу.
Хоть нижнее крыло и может создавать отрицательную подъёмную силу, но без работы нижнего крыла верхнее крыло так сильно бы не нагрузилось, образуя огромные застойные пузыри положительного и отрицательных давлений вокруг себя.
Особого внимания заслуживают веерные линии в зонах смены плотности воздуха (изменение градиента давления) при резком (ударном) изменении направления потока воздуха. При этом скорость воздуха практически постоянна по модулю (долями процента на сжатие-расширение потока пренебрегаем).
Данные зоны смены градиентов давления на шлирен-фотографиях видны как тёмные полоски. В традиционном объяснении Подъёмной силы крыла по Бернули эти веерные тёмные полосы объясняют ударными волнами на границах перехода на сверхзвуковое течении воздуха над крылом, что неверно (воздух там никуда бешенно не разгоняется, тем более до сверхзвука).
Вообще расчёт самолёта достаточно простая штука, а наличие абстрагированных безразмерных показателей Ккр, Су и Сх позволяет легко просчитывать общие показатели будущих самолётов практически на салфетке за несколько минут.
Расчёт № 1.
Попытаемся просчитать конструкцию и аэродинамику мускулолёта.
Главным ограничивающим фактором в конструкции мускулолёта является мускульная мощность человека, которую можно принять на уровне Nдв=250Вт в длительном режиме.
Это реалистичная оценка дана по мощности электровелосипедов, которые на такой мощности длительно едут со скоростью более 20км/ч, что значительно быстрее среднего человека на велосипеде на одних педалях.
Далее мы можем принять некий расчётный вес самого человека и вес конструкции: пусть это будет 75 кг и 75 кг.
Тогда общий взлётный вес составит m=150кг.
Сопротивление полёту зависит только от качества крыла, которое мы примем достаточно высоким на уровне Ккр=20 (сопротивление фюзеляжа пока не учитываем)
Тогда имеем силу сопротивления:
Fх=mg/Ккр=9,81*150/20=75Н
Исходя из располагаемой мощности 250 Вт можно получить доступную скорость взлёта, а именно:
Vвз=N/Fx=250/75=3,33м/с (11,8км/ч)
Зная скорость и характеристики профиля при Ккр=20, можем определить необходимую площадь крыла и соответствующий общий размах крыла.
Так исходя из ранее приведённых аэродинамических характеристик профиля типа А для Ккр=20 коэффициент подъёмной сила составит приблизительно Су=0,45.
При скорости взлёта V= 3,33м/с скоростной напор составит Pv= 3,33^2*1,2/2= 6,65Па
А площадь крыла потребуется S=m*g/(Су*Pv)=150*9,81/(0,45*6,65)=491м.кв.
Для монопланной схемы такое крыло длиной в 200-500м вообще выглядит запредельно длинным, а весь проект неосуществимым.
А вот для полиплана крыло площадью 491 м.кв. превращается в квадратную этажерку с размером
L= ( S*2,5)^0,5=35м
Квадратная конструкция из крыльев с размером 35х35 м уже будет более реалистичной. При этом общий внешний размер квадратной «этажерки» не изменится при выборе широких или узких крыльев в её заполнении.
Хотя я слабо представляю себе из чего сделать крылья общей площадью 491 м.кв + вертикальные стойки схожего погонажа, при этом вписавшись в общий вес менее 75 кг, или около 0,15 кг/м.кв.
При относительной толщине даже 9% крыло из лёгкого пенопласта с плотностью 35кг/м3 уже будет весить около 1,5кг/м.кв. или в 10 раз тяжелее допустимого.
То есть технически практически не достижимы нужные для мускулолёта массо-габаритные характеристики его несущих конструкций.
Так даже обтяжка профиля с двух сторон плёночным лавсаном (плёнка липкой ленты) с плотностью 1400кг/м3 и толщиной всего 0,1мм, даёт уже около 0,28кг/м2 площади крыла.
А ведь ещё и прочный каркас будет что-то весить!
То есть полиплан-мускулолёт должен трансформироваться в подобие воздушного змея из тонюсеньких плёночек толщиной менее 0,05мм из прочнейших полимеров и тонкого каркаса из углепластика. Воздушного змея подобной полипланно-плёночной конструкции можно посмотреть на фото (см.фото.рис.32).

Рис.32. Воздушный змей полипланно- плёночной конструкции(крыло нулевой толщины).
Расчёт № 2.
Проведём альтернативный расчёт, изменив качество крыла в сторону уменьшения, но при этом подняв Су профиля.
Так тот же профиль типа А-18% при качестве крыла Ккр=12,5 обеспечивает Су=1,06.
Повторяем расчёт при новых характеристиках.
Fх=mg/Ккр=9,81*150/12,5=117,7Н
Тогда доступная скорость составит
Vвз=N/Fx=250/117,7=2,12м/с (7,6км/ч)
При скорости взлёта Vвз= 2,12м/с скоростной напор составит Pv= 2,12^2*1,2/2= 2,69Па
А потребная площадь крыла будет:
S=m*g/ (Су*Pv)=150*9,81/ (1,06*2,69)=516м.кв.
То есть удивительным образом цифра общей площади крыла практически не изменилась при одинаковой мощности двигателя, но при разном качестве крыла.
Вывод :
Результаты двух расчётов однозначно показывают, что мускулолёты являются практически нереализуемыми конструкциями по массо-габаритным параметрам.
Но современные строители мускулолётов стараются выйти из этого конструктивного тупика, поднимая мощность на двигателе, то есть сажая в мускулолёт опытных и тренированных мужчин-велосипедистов, способных в течении длительного времени выдавать на педалях мощность до 1 кВт.
Для сравнения 1 кВт – это подъём со скоростью 1м/с по вертикали груза 100кг. То есть нужно иметь способность забежать по лестнице быстрее лифта (скорость лифта в 9-этажках равна 1м/с) с грузом на плечах (суммарно 100 кг массы от своего веса и груза на плечах). В юности я мог обогнать лифт бегом на 9-й этаж, но с 30 кг на плечах этого я бы уже не смог исполнить даже тогда.
В итоге на скоростях 7-8 м/с (25-28 км/ч) и с мощностью 1 кВт мускулолёт уменьшается по массе до 40-50кг и при размахе крыльев около 30м.
То есть если общий взлётный вес 120кг при качестве крыла Ккр=12, то сопротивление составляет Fу= 100Н, что на скорости 7м/с (25км/ч) требует мощности более 900Вт ( 700 Вт сопротивление крыла + потери в цепной передаче передаче и на КПД винта), скоростной напор Рv= 7^2*1,2/2=29Па позволяет лететь на крыле площадью 35-45м.кв при Су=1, 08 (характеристика планерного крыла P-III (15,5%) на угле атаке 12град, см. рис.9)
Мировой рекорд дальности для мускулолёта — это перелёт на расстояние 115 км за 3 часа 54 минуты 59 секунд (средняя скорость 29,36 км/ч) по маршруту с острова Крит на материк, который совершил греческий велосипедист-спортсмен K. Канеллопулос ( выступал за Грецию на летних Олимпийских играх 1984) на мускулолёте «MIT Daedalus » 23 апреля 1988 года. Аппарат имел размах крыльев 34,75 м, а площадь крыла составила 35,0 м².(см.рис.33)
При площади крыла всего 35м.кв и массе СЛА в 45 кг на 1 квадратный метр крыла приходится уже почти 1кг материала, то есть реально уже обтянуть профиль крыла двумя слоями лавсана по 0,05мм и останется ещё 800грамм на 1 м главного лонжерона (улепластиковая тонкостенная труба большого диаметра) и нервюру профиля из упрочнённого тонкослойного пенопласта.

Рис.33-а. Вид рекордного мускулолёта Дедал образца 1987года на испытаниях в пустыне Калифорнии.

Рис.33-б. Вид рекордного мускулолёта Дедал, который в 1988г совершил рекордный перелёт с о.Кипр на материк на дистанцию 115км.
Расчёт № 3.
Зато, если мы поднимем мощность двигателя всего до 3 кВт с собственным весом двигателя всего около 6 кг (мощность и вес двухтактной бензопилы), то наш летательный аппарат резко уменьшится
Так тот же профиль типа А-18% при качестве крыла Ккр=12,5 обеспечивает Су=1,06.
Повторяем расчёт при новых характеристиках.
Fх=mg/Ккр=9,81*150/12,5=117,7Н
Тогда доступная скорость составит
Vвз=N/Fx=3000/117,7=25,4м/с (или 91км/ч, как и у Ан-2)
При скорости взлёта Vвз= 25м/с скоростной напор составит Pv= 25^2*1,2/2= 375Па
При этом потребная площадь крыла будет:
S=m*g/ (Су*Pv)=150*9,81/ (1,06*375)=3,7м.кв
То есть даже с малюсеньким бензиновым двигателем в 3 кВт можно взлететь на самолётике с двумя маленькими крыльями, каждое размером как обычная межкомнатная дверь!
Расчёт № 4.
Если же поднять мощность авиационного двигателя всего до 20 кВт и увеличить взлётную массу самолёта до 300кг (200кг на саму конструкцию + 100кг на вес человека и топлива), то такой самолёт приобретёт вполне привычный вид лёгкого спортивного самолёта.
Так тот же профиль типа А-18% при качестве крыла Ккр=20 обеспечивает Су=0,45.
Повторяем расчёт при новых характеристиках.
Fх=mg/Ккр=9,81*300/20=150Н
Тогда доступная скорость составит
Vвз=N/Fx=20000/150=133м/с (или 480км/ч)
При скорости полёта V= 133 м/с скоростной напор составит Pv= 133^2*1,2/2= 10600Па
А потребная площадь крыла будет:
S=m*g/ (Су*Pv)=300*9,81/ (0,45*10600)=0,62м.кв
То есть два крыла, каждое размером всего 1,0х0,31м, на скорости 480км/могут удержать самолёт в полёте.
Видели малюсенькие крылышки у крылатых ракет, более похожих на торпеды с большими плавниками? (см.рис.34)
Так вот это реальные размеры «крыльев-плавников», которые вполне легко получаются простым расчётом!

Рис.34-а. Крылатая ракета с маленькими прямоугольными крыльями ( макет, вид сверху).

Рис.34-б. Крылатая ракета с маленькими прямоугольными крыльями (натуральный вид на выставочной площадке).
Расчёт № 5
От высокой скорости полёта можно перейти к меньшим скоростям на больших углах атаки.
Так тот же профиль типа А-18% при качестве крыла Ккр=9,4 обеспечивает Су=1,2
Повторяем расчёт при новых характеристиках.
Fх=mg/Ккр=9,81*300/9,4=313Н
Тогда доступная скорость составит
Vвз=N/Fx=20000/313=64м/с (или 230км/ч)
При скорости взлёта Vвз= 64 м/с скоростной напор составит Pv= 64^2*1,2/2= 2457Па
А потребная площадь крыла будет:
S=m*g/ (Су*Pv)=300*9,81/ (1,2*2457)=0,998м.кв
То есть два крыла, каждое размером всего 1,0х0,5м, на скорости 230км/ч могут обеспечить взлёт самолёта и удержать самолёт в полёте.
Такими характеристиками обладают современные лёгкие спортивные самолёты, только садятся и взлетают они на сильно меньших скоростях на больших УА при отклонённых вниз закрылках. Пример: Сверхлёгкий самолёт Colomban MC-15 Cri Cri (Cricket) (см.рис.35.а-г.)
Крейсерская скорость полёта 180 км/ч
Скорость сваливания 70 км/ч
Наилучшая скорость набора высоты 160 км/ч
Дистанция на посадке до полной остановки 250 м
Взлётная дистанция 200 м
Страна производитель Россия
Год выпуска 2017
Высота с хвостовой стойкой 1.5 м
Дальность полета с максимальной загрузкой 463 км
Мощность двигателя 30 л. с.
Длина разбега 200 м
Размах крыльев 4.9 м
Максимальный взлетный вес 170 кг
Площадь крыла 3.1 кв.м
Емкость топливных баков 40 л
Максимальная коммерческая загрузка 92 кг
Вес пустого 78 кг
Длина 3.9 м

Рис.35.а. ТТХ сверхлёгкого самолёта Colomban MC-15 Cri Cri (Cricket)

Рис.35.б. Заход на посадку с отклонёнными закрылками сверхлёгкого самолёта Colomban MC-15 Cri Cri (Cricket)

Рис.35.в. Фото на аэродроме сверхлёгкого самолёта Colomban MC-15 Cri Cri (Cricket) рядом с человеком и лёгким самолётом привычного размера для сравнения (вид сбоку).

Рис.35.г. Фото на аэродроме сверхлёгкого самолёта Colomban MC-15 Cri Cri (Cricket) рядом с лёгким самолётом привычного размера для сравнения (вид сзади).
Именно такие простые обосновывающие расчёты и определяли бурное развитие авиации после изобретения и начала массового выпуска достаточно компактных и мощных бензиновых двигателей.
Причём для расчёта не требуется глубокое понимание аэродинамики, а лишь достаточно таблиц коэффициентов Су и Сх от продувок профилей крыла в АДТ, которые проводились повсеместно в 1920-х.
Расчёт № 6
Из спортивного интереса можно провести оценочный расчёт для дальнего межконтинентального бомбардировщика с задачей доставки ядерной бомбы массой 10 тонн на дистанцию 10 тыс.км., после чего сравним результат расчёта с характеристикой реального Ту-95.
Так тот же профиль типа А-9% (см.рис.2. в начале главы) на углах атаки около 4 градусов Су=0,396 и Сх=0,154 обеспечивает качество крыла Ккр=25,7.
Дополнительно учтём сопротивление фюзеляжа, так что общее Ксам=16..18 ( у Ан-2 показатель Ксам=11, у современного А-320 уже Ксам=18, у свободно парящих планеров Кплан=30…50)
Масса самолёта при взлёте принята 180 тонн (80 тонн планер+ 90 топливо + 10 тонн бомба) как у известного нам Ту-95.
Повторяем расчёт при новых характеристиках.
Fх=mg/Ксам=9,81*180 000/16=110 360Н ( или 11 тонн тяги)
Пример крейсерскую скорость V=800км/ч (222м/c) на высоте 10км при плотности воздуха 0,42кг/м3. (см.рис.36)
Тогда мощность тяги составит N= Fx*V= 110 360*222=24 499 920 Вт (или 24,5 МВт или 32 тыс. л.с.)
С учётом КПД винта= 0,9 получим Nном=27МВт
Расход топлива у ДВС составляет 250г/(кВт*ч), таким образом, расход топлива самолёта на крейсерской скорости составит 27*0,25*1000=7500кг/ч
90 тонн запаса топлива обеспечивают 90/7,5=12 часов полёта, а дальность составит 12*800=9600км.
Реальная дальность полёта будет больше, так как с расходом топлива уменьшается масса самолёта и падает потребная мощность двигателя, увеличивая длительность полёта при том же запасе топлива. Так пустой самолёт к концу полёта будет тратить около 4тонн/ч, то есть средний расход составит 6т/ч, длительность полёта поднимется до 15ч, а дальность полёта вырастет до 15*800=12 тыс.км.
Теперь посчитаем площадь крыла.
Так при скорости 222м/с и плотности воздуха 0,42кг/м3 скоростной напор составит:
Pv = 222^2*0,42/2=10350Па
А потребная площадь крыла будет:
S=m*g/ (Су*Pv) =180 000*9,81/ (0,4*10350)=426 м.кв

Рис.36. Таблица давления и плотности воздуха по высоте от поверхности земли.
А теперь посмотрим реальные характеристики Ту-95. (см.рис.37-39)

Рис.37. Таблица характеристик самолёта Ту-95.

Рис.38. Общий вид самолёта Ту-95 (чертёж в трёх проекциях).
Сразу видно что мы вполне точно посчитали мощность двигателя ( 4х8948=36МВт, что оставляет запас мощности в 35-40% для взлётного режима), а значит при одинаковом запасе топлива в 90 тонн мы приняли правильное аэродинамическое качество Ксам и получили реалистичную дальность полёта.
Видно, что главное отличие наших расчётов от реального самолёта- это площадь крыла всего 289м.кв (против насчитанных нами 426м.кв) при средней нагрузке на крыло 640кг/м.кв (6,5кПа). То есть реальное крыло в 1,47 раза меньше по площади, чем у рассчитанного нами.
Из чего можно сделать вывод, что у реального Ту-95 показатель Су=0,6 при том же Ккр=20..25.
Противоречит ли это нашей нашей теории?
Нет, не противоречит!
В том же справочнике Авиационных профилей мы обнаруживаем профиль ЦАГИ-731 (толщина профиля 10,6%) (см. Таб. рис.39), у которого для угла атаки 6 градусов Су=0,604 при Сх=0,0288, что даёт нам Ккр=21.
На первый взгляд профили вообще не отличимы, но чуть большая толщина и тупоносость у профиля ЦАГИ -731 (10,6%) дают чуть более высокие Су и большую удельную грузоподъёмность при равных Ккр.
Он же для угла атаки 4 градуса Су=0,442 при Сх=0,0194, что даёт нам Ккр=22,8.
Он же для угла атаки 2 градуса Су=0,294 при Сх=0,0120, что даёт нам Ккр=24,5.



Рис.39. Сравнение профилей А-9% и ЦАГИ-731 (10.6%) из справочника и их характеристики Су и Сх с продувки в АДТ, где у профиля ЦАГИ-731 (10.6%) создаются большие Су при меньших УА и более высоких Ккр (большая удельная грузоподъёмность профиля).
То есть на обратном пути с бомбёжки, полегчав на половину запаса топлива и вес бомбы, Ту-95 начинает тратить уже в 1,5 раза меньше горючего в единицу времени. В конце же маршрута перед самым аэродромом с пустыми баками самолёт летит с часовым расходом топлива более чем в 2 раза меньше, чем при вылете с аэродрома на бомбёжку.
Итого:
Простейшим оценочным расчётом на нескольких листах бумаги и с применением простейшего калькулятора (арифмометра) мы добились практически 100% попадания нашего оценочного аэродинамического расчёта в реальные ТТХ реального стратегического бомбардировщика Ту-95. При этом сделали мы этот расчёт с опорой лишь на открытые справочные данные из 1930-х годов о продувках профилей крыла на АДТ, а также применив базу знаний из школьного курса физики раздел «механика».
Вернёмся к удельным массовым показателям конструкции самолёта. Так будем считать, что для Ту-95 доля самого планера без узлов шасси и двигателей составит половину сухого веса, что равно 40 тонн чистого авиационного дюраля с плотностью 2,7г/см3.
Считаем, что общая площадь поверхности крыльев (с двух сторон), фюзеляжа и хвостового оперения составляет около 1000 м2. Тогда на каждый квадратный метр поверхности придётся 40 000/1000= 40 кг алюминия, или лист толщиной 40/2,7=14мм. В итоге из такого количества алюминия мы можем получить однослойную общивку из листа 3-4мм, под которой с шагом в 200 мм будет установлен набор рёбер высотой 200мм с шагом 200мм в двух взаимно перпендикулярных направлениях. Такая ребристо-ячеистая конструкция планера вполне может выдержать распределённую нагрузку в 600кг/м2 в полёте. Примеры ребристого несущего усиления обшивки видны на фото (см.рис.40-43).

Рис.40. Силовой набор фюзеляжа пассажирского самолёта при изготовлении в цеху (полуфабрикат перед сборкой).

Рис.41. Силовой набор фюзеляжа пассажирского самолёта при изготовлении в цеху.

Рис. 42. Силовой набор крыла самолёта: опущенный бесщелевой закрыло-щиток на лёгком самолёте на стоянке в аэропорту.

Рис. 43. Силовой набор крыла большого авиалайнера в цеху.
Так что у огромных Ту-95 и малых лёгких самолётов со слабенькими бензиновыми движками даже в быстрой грубой оценке реалистичность конструкции значительно выше, чем у лёгких мускулолётов.
Часть № 7.
Гидродинамика полёта на подводном крыле на примере СПК " Ракета" Ростислава Алексеева (СССР).
Экономика пассажироперевозок на СПК в сравнении с рейсовым автобусом.
Сравнение СПК «Ракета» и СПК Боинг-929 (США).
Гидродинамика подводного крыла.
Полёт на крыльях возможен не только в воздушном пространстве, но и в водной среде.
К таким гидролётам относятся глиссирующие суда и суда на подводных крыльях (далее СПК).
Для этих двух типов быстроходных судов общим является гидродинамическое удержание над водой в процессе движения на крейсерской скорости.
В то же время на стоянке или на малых скоростях оба типа судов становятся обычными водоизмещающими судами.
С точки зрения гидро-газодинамики нам интересны больше суда на подводных крыльях, так как они осуществляют чистый полёт на тонких узких крыльях внутри водяного полупространства, а большой корпус с людьми и грузами летит сквозь воздух с малым сопротивлением (малым в сравнении с водоизмещающим режимом на той же скорости).
Для понимания гидродинамики подводного крыла крайне интересны диаграммы, найденные мной в публикации на тему подводных крыльев аж от 1964 года. (см.рис.2.)
Ссылка на источник:
Проектирование и расчет подводных крыльев (Судостроение / Технологии) — Barque.ru
При этом надо представлять что такое сегментный профиль относительной толщиной е=0,06 (или 6% от ширины). (см.рис.1): это узкий сегмент круга с угловой величиной 26 градусов (13*2=26) и углом схода поверхностей на острых кромках 13градусов.
13 градусов – это очень острое лезвие, приблизительно как у кавалерийской сабли.
При заданной ширине крыла 500мм толщина профиля 6% составляет 30мм. Радиус кривизны цилиндрической поверхности крыла составляет R=1056мм.

Рис.1. Вид сегментного профиля крыла СПК при ширине 500мм и относительной толщиной 6%.

Рис.2. Диаграммы характеристик Сх, Су, К сегментного крыла СПК в зависимости от глубины погружения и углов атаки.
Из диаграммы В) видно, что максимальное качество крыла составляет около К=16.
Экстремально высокий К=19 не рассматриваем, так как он относится к глубоко погружённому крылу с глубиной 2В (В- ширина крыла).
При интересующих нас глубинах погружения крыла 0,1-1В показатель Су=0,2-0,3 на углах атаки УА=2-4 градуса с максимально возможным К=16.
При попытке получить больший Су на больших углах атаки резко падает качество крыла К.
Удвоение Су приводит к снижению качества крыла до величины К=11.
Нам известно, что у СКП два основных режима движения:
1.Выход на глиссирование и вставание на крыло на малых скоростях 20 км/ч.
2.Крейсерская скорость 60км/ч на крыльях с полным отрывом корпуса от воды.
То есть на этих двух режимах нам нужно использовать разные кривые с разным соотношением К- Су с диаграммы.
При разгоне СПК на первом режиме наиболее применимы высокие Су=0,5-0,65 при К=11.
На крейсерской скорости нужно учитывать только кривую для малопогруженного крыла с низким Су=0,3 при высоком К=15.
Дополнительно нужно будет учесть сопротивление вертикальных стоек, на которых будет держаться несущее крыло, и сопротивление корпуса воздушному потоку на крейсерской скорости.
Сопротивление для стоек будет на уровне минимального Сх для подводного крыла с нулевым углом атаки.
Что из этого следует?
А следует то, что энергетическая эффективность судов на подводных крыльях оказывается такое же, как и у самолёта АН-2, который имеет качество планера целиком Кп=11 на крейсерской скорости 190км/ч.
То есть экономичнее круглый год летать на АН-2, чем всего полгода эксплуатировать на реках корабли на подводных крыльях.
Для эталонной ракеты со полной массой 24 тонны на крейсерской скорости 60км/ч при Су=0,3 и К=15 крыла нужна площадь подводных крыльев способная удержать СКП как на высоких скоростях, так и на низких стартовых.
Скоростной напор воды на крейсерской скорости 60км/ч составляет:
Р=(60/3,6)^2*1000/2=138900 Па=138,9 кПа или 14157кг/м2
То есть для крейсерского экономичного режима нужна площадь подводных крыльев:
S=24000/(0,3*14000)=5,7м.кв
Что при ширине крыла 500 мм составит длину крыльев почти 12 м.
А вот при выходе на крылья из водоизмещающего режима при скорости около 20км/ч крыльев нужно побольше.
Скоростной напор воды на крейсерской скорости 20км/ч составляет:
Р=(20/3,6)^2*1000/2=15430 Па=15,4кПа или 1572кг/м2
То есть для разгонного режима даже при в два раза большем Су=0,65 нужна площадь подводных крыльев почти в 4 раза больше:
S=24000/(0,65*1572)=23,5м.кв
Что соответствует длине крыла 47м при ширине 500мм.
Судя по фото «Ракеты» снизу (см.рис.3), где видна явная ширина подводного крыла и его можно сравнить с шириной окна в корпусе, при этом ширина окна составляет около 1м.
Получается что переднее крыло СПК имеет по факту ширину около 1,2м.
Тем самым при ширине корпуса в 5 м суммарная площадь двух крыльев превышает 12 м.кв.
То есть с выходом на глиссирование на больших углах атаки корпуса и с помощью дополнительных приспособлений в виде глиссадных лыж ( на фото (см. Рис.4-6) лыжи с брызгоотбойными экранами видны сразу за стойками передних крыльев) разгон и выход полностью на крылья вполне осуществим.

Рис.3. Вид на СПК «Ракета» снизу, где видна реальная ширина подводных крыльев.

Рис. 4.Вид на СПК «Ракета» спереди анфас, где хорошо видна глиссадная лыжа с брызговыми экранами позади передней стойки подводного крыла. На фото хорошо видно, что лыжа перестает касаться уровня воды только при очень малом заглублении подводного крыла.

Рис.5. СПК «Ракета» в стадии разгона, что видно по заметному погружению глиссадной лыжи в воду. Позади переднего подводного крыла под днищем СПК хорошо заметна водяная яма, образованная за счёт отброса воды вниз от подводного крыла.

Рис.6. СПК «Ракета» на полном ходу, что видно по полному поднятию из воды глиссадной лыжи. Позади переднего подводного крыла под днищем СПК хорошо виден бурный кавитационный след, который начинается мелкими пузырьками под водой на середине плоскости переднего подводного крыла( т.е. давление на верхней плоскости подводного крыла упало 0,02 атм, что соответствует кипению воды при +20С)
Исходя из полученных данных можно подобрать двигатель для условной «Ракеты» с полной массой 24 тонны.
На стартовом режиме со скорости 20км/ч при Кп=4 (режим глиссирования с сильно замоченным корпусом) мощность сопротивления составит
N=24000*9,81*20/(3,6*4)=327000Вт= 327кВт
На крейсерской скорости 60км/ч при Кп=15 (оптимистично) мощность сопротивления составит
N=24000*9,81*60/(3,6*15)=261600Вт= 262кВт
На крейсерской скорости 60км/ч нужно добавить лобовое сопротивление, которое для СПК с поперечным сечением около 20м.кв и коэффициентом лобового сопротивления Сд=0,8 (грубая оценка в сравнении с Сд=0,8 как у куба ребром на ветер, а у Шара Сд=0,5) составит:
Fвозд=20* (60/3,6)^2*0,8/2=2222Н или 227кгс
Мощность на воздушное сопротивление потребуется
Nвозд=2222*(60/3,6)=37033Вт=37кВт.
Сопротивление стоек опор крыла в количестве 6шт с высотой под водой 0,3 м, толщиной 40мм и лобовым сопротивлением Сд=0,015/0,06=0,25 составит
Fвод=0,25*6*0,3*0,040* (60/3,6)^2*1000/2=2500Н или 254кгс
Мощность на водяное сопротивление стоек потребуется
Nвозд=2500*(60/3,6)=41666Вт=42кВт.
Получается суммарная мощность сопротивления:
Nr=262+37+42=341кВт
Где 79 из 341 кВт или 23% общей мощности сопротивления движению приходится на сопротивление корпуса в воздухе и стоек опор крыла в воде.
Доля 23% потерь от стоек и корпуса в общих потерях — это означает падение общего гидродинамического качества СПК от К=15 (только для самого крыла) до К=15*(100-23)/100=11,55.
Таким образом СПК «Ракета» точно совпал с самолётом АН-2 по общему аэродинамическому качеству К=11,5
Мощность на разгоне при выходе на крыло(327 кВт) практически совпадает с необходимой мощностью на крейсерской скорости(341 кВт), что означает необходимость постоянной работы двигателя на номинальной мощности как на крейсерской скорости, так и при разгоне.
С учётом КПД винта и валопроводов на уровне n=0,5 для нашего СПК потребуется двигатель
Nдв =341/0,5=682 кВт или 927 л.с.
Для проверки заглядываем в википедию и видим близкую цифру мощности двигателя 900-1000л.с. (в зависимости от модификации) (см.рис.7).
Учитывая некоторые перезаклады по площади лобового сечения корпуса и высоту погружённых стоек на крейсерской скорости, то можно считать, что расчёты практически совпали с реальными ТТХ СПК «Ракета».

Рис.7. ТТХ СПК «Ракета» согласно Википедии.
Столь точное попадание нашего оценочного расчёта по диаграмме К-Су в справочные характеристики реального СПК «Ракета» позволяет сделать вывод о причинах резкого взлёта темы больших СПК в 1960-1970 годах в СССР и быстрый сход темы в 1990-х.
Причина угасания интереса к эксплуатации пассажирских СПК является чрезвычайная энергоёмкость, а потому и дороговизна перевозок, в сравнении с резко прибавившему в массовости шоссейному автотранспорту.
Расход топлива дизельным двигателем оценочно 200г/л.с.*ч
Для СПК с ДВС в 1000л.с. расход топлива составит 200*1000= 200кг/ч. или 235л/ч при плотности солярки 0,85кг/л.
За 1 час СПК преодолеет 60км на крейсерской скорости, при этом расход топлива составит 235л/65чел=3,61л/чел*60км
Аналогичный по вместимости пассажиров рейсовый автобус имеет ту же крейсерскую скорость в 60км/ч, но при этом расход топлива в 13-22 раз меньше в пересчёте на одного пассажира*км.
В такой же пропорции 20:1 соотносятся и стоимости созданных по авиационным технологиям алюминиево-титановых СПК со стоимостью производства обычных железных рейсовых автобусов, что также не добавляет конкурентных качеств для СПК.
Сравним реальные образцы массовых автобусов времён позднего СССР по топливной экономичности на одного пассажира с СПК.
ЛиАЗ-677 имел мощность ДВС 180л.с…
Контрольный расход топлива ЛиАЗ-677 при 40 км/ч — 35,0 литров на 100 км, или 14л/ч, или 21л/60км пробега.
В пересчёте на человека на дистанции 60 км получим показатель 21/80=0,262 л/(чел*60км)
В сравнении с СПК «Ракета» автобус ЛИАЗ-677 экономичнее в 3,61/0,262=13,7 раз
Его современник Икарус-280 (гармошка) был в 2 раза более вместительным (146чел) при этом имел расход всего 40л на 100км/пути при 60км/ч, что в пересчёте на 60км пробега расход составит всего 40*60/100=24л/(60км).
В пересчёте на человека на дистанции 60км получим 24/146=0,164 л/(чел*60км)
В сравнении с СПК «Ракета» автобус Икарус-280 экономичнее в 3,61/0,164=22 раз

Рис. 8. ТТХ городского рейсового автобуса ЛиАЗ-677 согласно Википедии.

Рис. 9. ТТХ городского рейсового автобуса Икарус-280 (гармошка) согласно Википедии.
По итогу можно сказать, что ЛЕТАТЬ на короткие расстояния — это ДОРОГО.
И не важно где ваши крылья находятся: в воде или в небе, — в итоге вы всё равно проиграете легковому автомобилю или автобусу на дистанции до 500км.
На дистанциях 500-1500 км по экономичности в равных предпочтениях самолёт или поезд.
На расстояние дальше 1500км (сутки на поезде) однозначно уже выгоднее летать дальней авиацией на современных аэробусах.
Правда тут в экономику входят не только топливо, но и расход времени пассажира. Так большинство людей не готовы ехать целую неделю в поезде из Москвы до Владивостока, если туда же можно долететь всего за сутки, даже с учётом доезда поездом или автобусом до не самого ближнего аэропорта, с учётом прибытия за 3 часа до рейса и 9 часов самого чистого полёта.
Аналогичную с СПК судьбу имела малая региональная авиация на самолётах типа АН-2: она вымерла в конкурентной борьбе с автобусами и расплодившимися личными автомобилями, которые оказались на много удобнее в пользовании на резко улучшившихся асфальтовых дорогах.
Но даже в эпоху СССР речные СПК не могли заменить регулярное пригородное сообщение по суше, так как на зиму навигация останавливалась. В результате СПК стали дотируемым государством транспортным аттракционом, которым пользовались житель приречных городов.
Чаще всего СПК возили дачников по выходным дням на отдалённые 6-соточные участки, отрезанные от города рекой и не имеющие близкого по расстоянию альтернативного автомобильно-автобусного маршрута.
Сравнение СПК «Ракета» с аналогами из США на примере СПК Боинг-929
Но что у конкурентов на Западе?
В условиях глобального противостояния сверхдержав США не могли не ответить технологическому вызовы от СССР. В результате в 1974 году на свет появился американский СПК от авиационной компании Боинг.

Рис.10. ТТХ СПК Боинг -929 согласно Википедии.
СПК Боинг 929 должен был во всех показателях опережать «этих советских», и это Боингу удалось (см.рис.6)
-Он был быстрее«Ракеты» (80км/ч против 70 км/ч у ),
— он был в 4 раза тяжелей «Ракеты» (104 т против 25 тонн)
— он брал на борт в 5,4 раза больше пассажиров (350 чел против 65 чел)
— он имел два двигателя (газотурбинные авиационные двигатели) по 3400кВт каждый или около 6800 кВт (9250л.с) в пиковом режиме суммарно, что в 9 раз больше, чем один двигатель «Ракеты».
— он потреблял в 9 раз больше топлива в час (2150л/ч против 235л/ч)
Особенно мне нравится последний пункт про гигантский часовой расход топлива, но корректнее будет пересчитать на одного пассажира на стандартном для нашего сравнения 60км маршруте.
Так на одного пассажира СПК Боинг 929 потратит Мт=2150*60/(80*350)=4,6 л/(чел* 60км)
То есть по итогу Боинг 929 проиграл «Ракете» по топливной экономичности в
4,6/3,61=1,27 раза.
С учётом конструктивных особенностей двигателя и движителя Боинга 929 такая разница вполне закономерна.
В качестве двигателей американцы применили авиационные турбины вместо судовых дизелей. Турбины очень лёгкие и мощные в сравнении с дизельными двигателями, но очень прожорливы на неноминальных режимах, что снижает общую топливную экономичность судна на коротких маршрутах, где доля времени на маневрирование в водоизмещем режиме достаточно велика.
В качестве движителя был использован водомёт, что также понизило итоговый КПД системы.
В целом данные решения закономерны, так как американские конструкторы СПК сразу начали проектировать «Водяной самолёт», а не корабль (см.Рис.10. — название типа: «самолёт на подводных крыльях»).
В технических решениях это оказался именно «самолёт» с богатой механизацией крыла.
Так у Боинга 929 были установлены закрылки, облегчающих «взлёт» из воды на малых скоростях. (см рис.12,13,14)
Были у Боинга и подводные элероны, позволяющих совершать маневры по-самолётном, закладывая на высокой скорости вираж с креном внутрь круга.(см рис.17).
При этом на советских СПК подводные крылья механизацией не оснащали.
Советские СПК в повороте имели сильный крен наружу из поворота (как у обычных водоизмещающих кораблей и автомобилей). Для удержание от опрокидывания в поворотах с креном судна наружу использовали принципы остойчивости по-корабельному, то есть восстанавливающий момент против крена наружу из поворота создавался гидродинамическим усилением подъёмной силы наружной части крыла при большем его заглублении в воду при крене.
Не смотря на своё техническое совершенств более технически сложный и дорогой СПК Боинг 929 в итоге разделил судьбу более простых и более экономичных СПК из СССР.
Низкая топливная экономичность даже для американцев стала убийственным фактором в судьбе СПК Боинг.
После нескольких лет эксплуатации в 1970-80х годах СПК Боинг 929 ушли со сцены.
В наше время в тёплых островных государствах без долгих морозных зим (Греция, Индонезия) тема быстроходных пассажирских СПК иногда периодически всплывает вновь, но при этом не выходит за рамки туристических аттракционов для «пляжных туристов».

Рис.11. Фото СПК Боинг -929 на полном ходу. Хорошо видна мощная струя воды из водомёта на корме выше уровня воды.

Рис.12. Схема крыльев и силовой установки СПК Боинг -929. На схеме показаны подводный водозабор на средней стойке заднего крыла, маршрут движения воды к водомётам, и управляемы закрылки на подводных крыльях.

Рис.13. Схема крыльев и силовой установки СПК Боинг -929 в сопряжении с корпусом судна. На схеме показаны подводный водозабор на средней стойке заднего крыла, маршрут движения воды к водомётам, и управляемы закрылки на подводных крыльях. Рулевым пером является поворотна стойка переднего подводного крыла (угол поворота+-5,5 град).

Рис.14. Общий вид СПК Боинг -929 с указанием уровня воды на крейсерской скорости.Хорошо видно, что американцы использовали глубоко погруженные подводные крылья с высоким Су, в отличии от мелкопогружённых крыльев СПК авторства Ростислава Алексеева и других СПК из СССР.

Рис.15. Фото переднего подводного крыла СПК Боинг 929 в поднятом из воды положении. Хорошо видны регулируемы закрылки на подводном крыле.

Рис.16. Чертёж в разных видах СПК Боинг -929. На виде на корму хорошо видны отверстия водомётов в корпусе, и их положение относительно уровня воды в водоизмещающем режиме и в полёте на крыле. Также можно замерить относительную глубину погружения крыла составляющую приблизительно 1,5В.

Рис.17. Чертёж вида сбоку СПК Боинг -929. На виде обозначены основные элементы СПК.

Рис.18. Фото СПК Боинг -929 на полном ходу в момент поворота. Хорошо виден крен судна в сторону центра поворота, что означает маневрирование с виражами по-самолётному. то есть преднамеренным созданием крена в повороте с помощью разнонаправленного движения закрылков. В то же время СПК Алексеева (с малозаглублённым крылом без управляемых закрылков) в повороте имели крен наружу из круга циркуляции, то есть компенсация центростремительного ускорения осуществлялось средствами гидродинамической остойчивости «по-судостроительному».
Библиография:
- «Гидравлика и аэродинамика», Альтшуль А.Д., Москва, Стройиздат, 1986.-413с.
- «Аэродинамика» часть 1, Краснов Н.Ф., Москва, Ленанд, 2018,-496с.
- «Аэродинамика», Под ред. Калугина В.Т., Москва, МГТУим.Н.Э.Баумана,2017,-607с.