I’m going to have a guess and say that everyone whose friends or family have ever flown on a plane, have used Flightradar24 — a free and convenient service for tracking flights in real time.

In the first part the basic ideas of operation were described. Now let's go further and figure out, what data is exactly transmitting and receiving between the aircraft and a ground station. We'll also decode this data using Python.
It should be obvious that airplanes data is not intended only for users, who want to see it on their smartphones. This system is called ADS–B (Automatic dependent surveillance—broadcast), and was designed for the automatic transmitting of the aircraft information data to the control center — different parameters, as coordinates, speed, heading, altitude, and others, are sending. Previously, the dispatcher could see only a point on the radar screen. And it became definitely not enough when number of airplanes drastically increased.
Technically, ADS-B consists of a transmitter inside the aircraft, that periodically sends information data frames at a relatively high frequency of 1090 MHz (there are some other modes, but they are not so interesting to us, because the coordinates are transmitted only here). Of course, there is also a receiver somewhere at the airport, but for us, as for users, our own receiver is more interesting.
Just for comparison, the first such a system designed for ordinary users, the Airnav Radarbox, appeared in 2007, and costed about $900, and about $250 per year costed a subscription to their network services (the main idea of this system is to collect and share data from many receivers, a standalone receiver is relatively useless).

Now, when RTL-SDR receivers have become much more available, a similar device can be made for $30. It can be found in the first part of the article, and we will go further and describe the protocol itself — let's see how it works.
First, we need to record a signal sample. The whole signal has only 120 microseconds length, and to see its details in a good «resolution», its better to have SDR-radio with at least 5MHz sample rate.
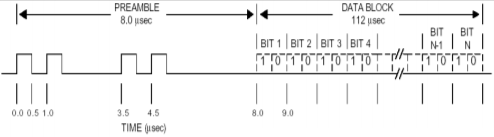
After recording, we are getting a WAV-file with a 5000000 samples/sec sampling rate, 30 seconds of such a record has about 500MB size. Of course, it’s useless to listen it with your favorite media player — the file does not contain a sound, but a directly digitized radio signal itself — this is exactly how Software Defined Radio works.
We can open and process this file with Python. Those who wish to do the experiment on their own, can download a sample from this link.
Lets open a file and see, what is inside.
Result: we see some 'impulses' over the noise.
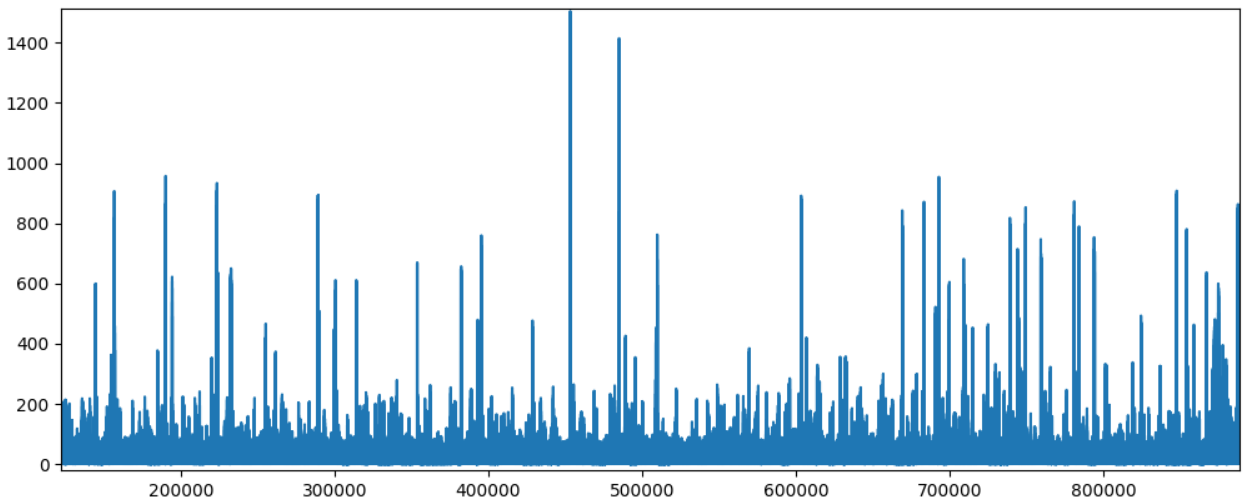
Each «impulse» is a signal, whose structure is clearly visible if we increase the resolution on the graph.
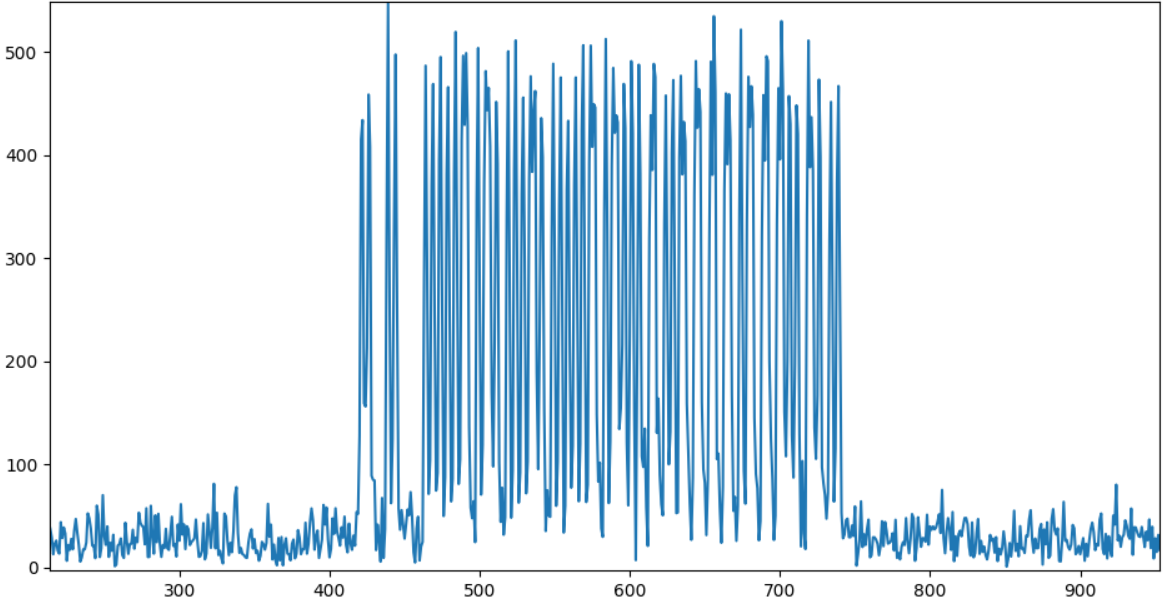
As we can see, the picture is fully consistent with its description above. We can now process this data.
First, we need to have a bit stream. The signal itself is encoded with a manchester encoding:

From the half-bite differences we can easily get real «0» and «1»'s.
The structure of the signal itself looks like this:

Lets see the fields in more detail.
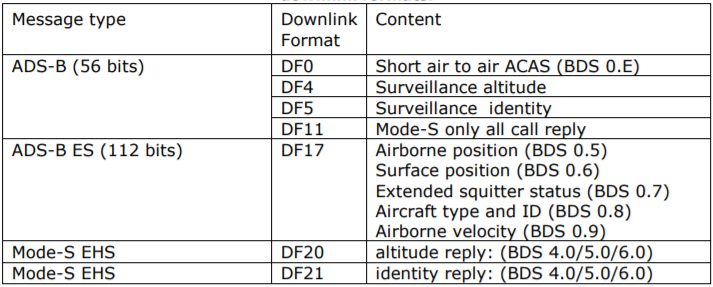
DF (Downlink Format, 5 bits) — defines the type of message. There are several types of them:
(page source)
We are only interested in the DF17 type, because only this one contains the aircraft coordinates.
ICAO (24 bits) — is an unique international aircraft code. We can check the aircraft by its code on this website (unfortunately, the author has stopped updating the database, but it is still relevant). For example, for the 3c5ee2 code we can have the following information:

DATA (56 or 112 bits) — is the data itself, which we will decode. The first 5 bits of data is the Type Code field, which contains the subtype of the data being stored (not to be mixed with DF field). There are a lot of such types:
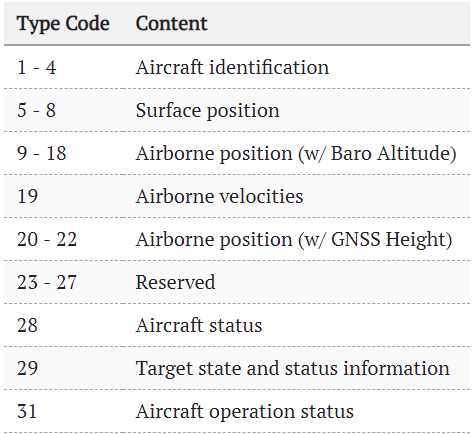
(table source)
Let's look at some examples.
Aircraft identification
An example in binary form:
00100 011 000101 010111 000111 110111 110001 111000
Data fields:
TC = 00100b = 4, and each symbol C1-C8 contains codes, that should match the indexes in this string:
#ABCDEFGHIJKLMNOPQRSTUVWXYZ#####_###############0123456789######
After decoding its easy to get the aircraft name: EWG7184
Airborne position
The name decoding was simple, but the coordinates are more complicated. They are transmitted in the form of 2 frames, even and odd. The field code TC = 01011b = 11.
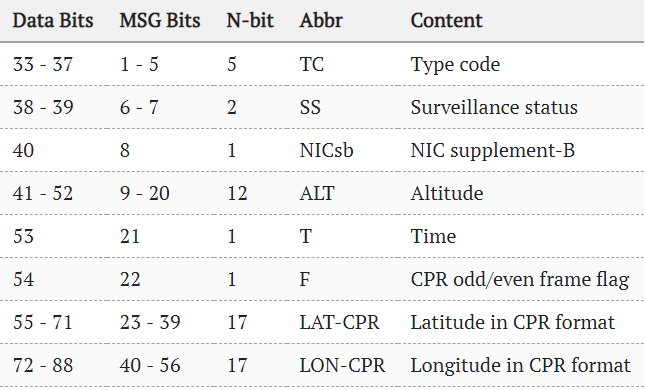
Example of even and odd data frames:
The calculation of the coordinates itself uses a bit tricky formula:

(source)
I am not a GIS expert, so I don't know where it comes from. Who knows it better, please write in comments.
The altitude calculation is simpler — depending on a specific bit, it can be represented as either a multiple of 25 or 100 feet.
Airborne Velocity
Dataframe with TC = 19. The interesting thing here is that the speed can be relative to the ground (more accurate, called Ground Speed), and Airspeed, measured by the aircraft air sensor (can be less accurate because of the wind). Many other different fields are also transmitted:

(source)
As we can see, ADS-B technology has become an interesting symbiosis, when a standard is widely usable not only for professionals, but also for ordinary users. But definitely, the key role in this was done by the cheapening of the of digital SDR receivers technology, which allows to receive signals with a frequency higher than gigahertz on a very cheap device.
The standard itself, of course, has much more data. Those interested can view the PDF on the page ICAO or visit the mode-s.org website already mentioned above. It is unlikely that this article will be really used by most of readers, but I hope, at least the general idea of how it works, is now more clear.
By the way, the ADS-B Python decoder already exists, it can investigated on the github. SDR receivers owners can also build and run ready-to-use ADS-B decoder from this page , and (I'll repeat again) some details we also in the first part of this article.
The parser source code, described above, is given under the spoiler. This is just a test example that does not pretend to production quality, but in general it works, and it can parse the WAV-file, recorded above.
I hope it was useful, thanks for reading.

In the first part the basic ideas of operation were described. Now let's go further and figure out, what data is exactly transmitting and receiving between the aircraft and a ground station. We'll also decode this data using Python.
History
It should be obvious that airplanes data is not intended only for users, who want to see it on their smartphones. This system is called ADS–B (Automatic dependent surveillance—broadcast), and was designed for the automatic transmitting of the aircraft information data to the control center — different parameters, as coordinates, speed, heading, altitude, and others, are sending. Previously, the dispatcher could see only a point on the radar screen. And it became definitely not enough when number of airplanes drastically increased.
Technically, ADS-B consists of a transmitter inside the aircraft, that periodically sends information data frames at a relatively high frequency of 1090 MHz (there are some other modes, but they are not so interesting to us, because the coordinates are transmitted only here). Of course, there is also a receiver somewhere at the airport, but for us, as for users, our own receiver is more interesting.
Just for comparison, the first such a system designed for ordinary users, the Airnav Radarbox, appeared in 2007, and costed about $900, and about $250 per year costed a subscription to their network services (the main idea of this system is to collect and share data from many receivers, a standalone receiver is relatively useless).

Now, when RTL-SDR receivers have become much more available, a similar device can be made for $30. It can be found in the first part of the article, and we will go further and describe the protocol itself — let's see how it works.
Receiving a signal
First, we need to record a signal sample. The whole signal has only 120 microseconds length, and to see its details in a good «resolution», its better to have SDR-radio with at least 5MHz sample rate.

After recording, we are getting a WAV-file with a 5000000 samples/sec sampling rate, 30 seconds of such a record has about 500MB size. Of course, it’s useless to listen it with your favorite media player — the file does not contain a sound, but a directly digitized radio signal itself — this is exactly how Software Defined Radio works.
We can open and process this file with Python. Those who wish to do the experiment on their own, can download a sample from this link.
Lets open a file and see, what is inside.
from scipy.io import wavfile
import matplotlib.pyplot as plt
import numpy as np
fs, data = wavfile.read("adsb_20190311_191728Z_1090000kHz_RF.wav")
data = data.astype(float)
I, Q = data[:, 0], data[:, 1]
A = np.sqrt(I*I + Q*Q)
plt.plot(A)
plt.show()
Result: we see some 'impulses' over the noise.

Each «impulse» is a signal, whose structure is clearly visible if we increase the resolution on the graph.

As we can see, the picture is fully consistent with its description above. We can now process this data.
Decoding
First, we need to have a bit stream. The signal itself is encoded with a manchester encoding:

From the half-bite differences we can easily get real «0» and «1»'s.
bits_str = ""
for p in range(8):
pos = start_data + bit_len*p
p1, p2 = A[pos: pos + bit_len/2], A[pos + bit_len/2: pos + bit_len]
avg1, avg2 = np.average(p1), np.average(p2)
if avg1 < avg2:
bits_str += "0"
elif avg1 > avg2:
bits_str += "1"
The structure of the signal itself looks like this:

Lets see the fields in more detail.
DF (Downlink Format, 5 bits) — defines the type of message. There are several types of them:

(page source)
We are only interested in the DF17 type, because only this one contains the aircraft coordinates.
ICAO (24 bits) — is an unique international aircraft code. We can check the aircraft by its code on this website (unfortunately, the author has stopped updating the database, but it is still relevant). For example, for the 3c5ee2 code we can have the following information:

DATA (56 or 112 bits) — is the data itself, which we will decode. The first 5 bits of data is the Type Code field, which contains the subtype of the data being stored (not to be mixed with DF field). There are a lot of such types:

(table source)
Let's look at some examples.
Aircraft identification
An example in binary form:
00100 011 000101 010111 000111 110111 110001 111000
Data fields:
+------+------+------+------+------+------+------+------+------+------+
| TC,5 | EC,3 | C1,6 | C2,6 | C3,6 | C4,6 | C5,6 | C6,6 | C7,6 | C8,6 |
+------+------+------+------+------+------+------+------+------+------+
TC = 00100b = 4, and each symbol C1-C8 contains codes, that should match the indexes in this string:
#ABCDEFGHIJKLMNOPQRSTUVWXYZ#####_###############0123456789######
After decoding its easy to get the aircraft name: EWG7184
symbols = "#ABCDEFGHIJKLMNOPQRSTUVWXYZ#####_###############0123456789######"
code_str = ""
for p in range(8):
c = int(bits_str[8 + 6*p:8 + 6*(p + 1)], 2)
code_str += symbols[c]
print("Aircraft Identification:", code_str.replace('#', ''))
Airborne position
The name decoding was simple, but the coordinates are more complicated. They are transmitted in the form of 2 frames, even and odd. The field code TC = 01011b = 11.

Example of even and odd data frames:
01011 000 000101110110 00 10111000111001000 10000110101111001
01011 000 000110010000 01 10010011110000110 10000011110001000
The calculation of the coordinates itself uses a bit tricky formula:

(source)
I am not a GIS expert, so I don't know where it comes from. Who knows it better, please write in comments.
The altitude calculation is simpler — depending on a specific bit, it can be represented as either a multiple of 25 or 100 feet.
Airborne Velocity
Dataframe with TC = 19. The interesting thing here is that the speed can be relative to the ground (more accurate, called Ground Speed), and Airspeed, measured by the aircraft air sensor (can be less accurate because of the wind). Many other different fields are also transmitted:

(source)
Conclusion
As we can see, ADS-B technology has become an interesting symbiosis, when a standard is widely usable not only for professionals, but also for ordinary users. But definitely, the key role in this was done by the cheapening of the of digital SDR receivers technology, which allows to receive signals with a frequency higher than gigahertz on a very cheap device.
The standard itself, of course, has much more data. Those interested can view the PDF on the page ICAO or visit the mode-s.org website already mentioned above. It is unlikely that this article will be really used by most of readers, but I hope, at least the general idea of how it works, is now more clear.
By the way, the ADS-B Python decoder already exists, it can investigated on the github. SDR receivers owners can also build and run ready-to-use ADS-B decoder from this page , and (I'll repeat again) some details we also in the first part of this article.
The parser source code, described above, is given under the spoiler. This is just a test example that does not pretend to production quality, but in general it works, and it can parse the WAV-file, recorded above.
Source Code (Python)
from __future__ import print_function
from scipy.io import wavfile
from scipy import signal
import matplotlib.pyplot as plt
import numpy as np
import math
import sys
def parse_message(data, start, bit_len):
max_len = bit_len*128
A = data[start:start + max_len]
A = signal.resample(A, 10*max_len)
bits = np.zeros(10*max_len)
bit_len *= 10
start_data = bit_len*8
# Parse first 8 bits
bits_str = ""
for p in range(8):
pos = start_data + bit_len*p
p1, p2 = A[pos: pos + bit_len/2], A[pos + bit_len/2: pos + bit_len]
avg1, avg2 = np.average(p1), np.average(p2)
if avg1 < avg2:
bits_str += "0"
elif avg1 > avg2:
bits_str += "1"
df = int(bits_str[0:5], 2)
# Aircraft address (db - https://junzis.com/adb/?q=3b1c5c )
bits_str = ""
for p in range(8, 32):
pos = start_data + bit_len * p
p1, p2 = A[pos: pos + bit_len / 2], A[pos + bit_len / 2: pos + bit_len]
avg1, avg2 = np.average(p1), np.average(p2)
if avg1 < avg2:
bits_str += "0"
elif avg1 > avg2:
bits_str += "1"
# print "Aircraft address:", bits_str, hex(int(bits_str, 2))
address = hex(int(bits_str, 2))
# Filter specific aircraft (optional)
# if address != "0x3c5ee2":
# return
if df == 16 or df == 17 or df == 18 or df == 19 or df == 20 or df == 21:
# print "Pos:", start, "DF:", msg_type
# Data (56bit)
bits_str = ""
for p in range(32, 88):
pos = start_data + bit_len*p
p1, p2 = A[pos: pos + bit_len/2], A[pos + bit_len/2: pos + bit_len]
avg1, avg2 = np.average(p1), np.average(p2)
if avg1 < avg2:
bits_str += "0"
# bits[pos + bit_len / 2] = 50
elif avg1 > avg2:
bits_str += "1"
# http://www.lll.lu/~edward/edward/adsb/DecodingADSBposition.html
# print "Data:"
# print bits_str[:8], bits_str[8:20], bits_str[20:22], bits_str[22:22+17], bits_str[39:39+17]
# Type Code:
tc, ec = int(bits_str[:5], 2), int(bits_str[5:8], 2)
# print("DF:", df, "TC:", tc)
# 1 - 4 Aircraft identification
# 5 - 8 Surface position
# 9 - 18 Airborne position (w/ Baro Altitude)
# 19 Airborne velocities
if tc >= 1 and tc <= 4: # and (df == 17 or df == 18):
print("Aircraft address:", address)
print("Data:")
print(bits_str[:8], bits_str[8:14], bits_str[14:20], bits_str[20:26], bits_str[26:32], bits_str[32:38], bits_str[38:44])
symbols = "#ABCDEFGHIJKLMNOPQRSTUVWXYZ#####_###############0123456789######"
code_str = ""
for p in range(8):
c = int(bits_str[8 + 6*p:8 + 6*(p + 1)], 2)
code_str += symbols[c]
print("Aircraft Identification:", code_str.replace('#', ''))
print()
if tc == 11:
print("Aircraft address:", address)
print("Data: (11)")
print(bits_str[:8], bits_str[8:20], bits_str[20:22], bits_str[22:22+17], bits_str[39:39+17])
# Bit 22 contains the F flag which indicates which CPR format is used (odd or even)
# First frame has F flag = 0 so is even and the second frame has F flag = 1 so odd
# f = bits_str[21:22]
# print("F:", int(f, 2))
# Altitude
alt1b = bits_str[8:20]
if alt1b[-5] == '1':
bits = alt1b[:-5] + alt1b[-4:]
n = int(bits, 2)
alt_ft = n*25 - 1000
print("Alt (ft)", alt_ft)
# lat_dec = int(bits_str[22:22+17], 2)
# lon_dec = int(bits_str[39:39+17], 2)
# print("Lat/Lon:", lat_dec, lon_dec)
# http://airmetar.main.jp/radio/ADS-B%20Decoding%20Guide.pdf
print()
if tc == 19:
print("Aircraft address:", address)
print("Data:")
# print(bits_str)
print(bits_str[:5], bits_str[5:8], bits_str[8:10], bits_str[10:13], bits_str[13] ,bits_str[14:24], bits_str[24], bits_str[25:35], bits_str[35:36], bits_str[36:65])
subtype = int(bits_str[5:8], 2)
# https://mode-s.org/decode/adsb/airborne-velocity.html
spd, hdg, rocd = -1, -1, -1
if subtype == 1 or subtype == 2:
print("Velocity Subtype 1: Ground speed")
v_ew_sign = int(bits_str[13], 2)
v_ew = int(bits_str[14:24], 2) - 1 # east-west velocity
v_ns_sign = int(bits_str[24], 2)
v_ns = int(bits_str[25:35], 2) - 1 # north-south velocity
v_we = -1*v_ew if v_ew_sign else v_ew
v_sn = -1*v_ns if v_ns_sign else v_ns
spd = math.sqrt(v_sn*v_sn + v_we*v_we) # unit in kts
hdg = math.atan2(v_we, v_sn)
hdg = math.degrees(hdg) # convert to degrees
hdg = hdg if hdg >= 0 else hdg + 360 # no negative val
if subtype == 3:
print("Subtype Subtype 3: Airspeed")
hdg = int(bits_str[14:24], 2)/1024.0*360.0
spd = int(bits_str[25:35], 2)
vr_sign = int(bits_str[36], 2)
vr = int(bits_str[36:45], 2)
rocd = -1*vr if vr_sign else vr # rate of climb/descend
print("Speed (kts):", spd, "Rate:", rocd, "Heading:", hdg)
print()
# print()
def calc_coordinates():
def _cprN(lat, is_odd):
nl = _cprNL(lat) - is_odd
return nl if nl > 1 else 1
def _cprNL(lat):
try:
nz = 15
a = 1 - math.cos(math.pi / (2 * nz))
b = math.cos(math.pi / 180.0 * abs(lat)) ** 2
nl = 2 * math.pi / (math.acos(1 - a/b))
return int(math.floor(nl))
except:
# happens when latitude is +/-90 degree
return 1
def floor_(x):
return int(math.floor(x))
lat1b, lon1b, alt1b = "10111000111010011", "10000110111111000", "000101111001"
lat2b, lon2b, alt2b = "10010011101011100", "10000011000011011", "000101110111"
lat1, lon1, alt1 = int(lat1b, 2), int(lon1b, 2), int(alt1b, 2)
lat2, lon2, alt2 = int(lat2b, 2), int(lon2b, 2), int(alt2b, 2)
# 131072 is 2^17, since CPR lat and lon are 17 bits each
cprlat_even, cprlon_even = lat1/131072.0, lon1/131072.0
cprlat_odd, cprlon_odd = lat2/131072.0, lon2/131072.0
print(cprlat_even, cprlon_even)
j = floor_(59*cprlat_even - 60*cprlat_odd)
print(j)
air_d_lat_even = 360.0 / 60
air_d_lat_odd = 360.0 / 59
# Lat
lat_even = float(air_d_lat_even * (j % 60 + cprlat_even))
lat_odd = float(air_d_lat_odd * (j % 59 + cprlat_odd))
if lat_even >= 270:
lat_even = lat_even - 360
if lat_odd >= 270:
lat_odd = lat_odd - 360
# Lon
ni = _cprN(lat_even, 0)
m = floor_(cprlon_even * (_cprNL(lat_even)-1) - cprlon_odd * _cprNL(lat_even) + 0.5)
lon = (360.0 / ni) * (m % ni + cprlon_even)
print("Lat", lat_even, "Lon", lon)
# Altitude
# Q-bit (bit 48) indicates whether the altitude is encoded in multiples of 25 or 100 ft (0: 100 ft, 1: 25 ft)
# The value can represent altitudes from -1000 to +50175 ft.
if alt1b[-5] == '1':
bits = alt1b[:-5] + alt1b[-4:]
n = int(bits, 2)
alt_ft = n*25 - 1000
print("Alt (ft)", alt_ft)
fs, data = wavfile.read("adsb_20190311_191728Z_1090000kHz_RF.wav")
T = 1/fs
print("Sample rate %f MS/s" % (fs / 1e6))
print("Cnt samples %d" % len(data))
print("Duration: %f s" % (T * len(data)))
data = data.astype(float)
cnt = data.shape[0]
# Processing only part on file (faster):
# cnt = 10000000
# data = data[:cnt]
print("Processing I/Q...")
I, Q = data[:, 0], data[:, 1]
A = np.sqrt(I*I + Q*Q)
bits = np.zeros(cnt)
# To see scope without any processing, uncomment
# plt.plot(A)
# plt.show()
# sys.exit(0)
print("Extracting signals...")
pos = 0
avg = 200
msg_start = 0
# Find beginning of each signal
while pos < cnt - 16*1024:
# P1 - message start
while pos < cnt - 16*1024:
if A[pos] < avg and A[pos+1] > avg and pos - msg_start > 1000:
msg_start = pos
bits[pos] = 100
pos += 4
break
pos += 1
start1, start2, start3, start4 = msg_start, 0, 0, 0
# P2
while pos < cnt - 16*1024:
if A[pos] < avg and A[pos+1] > avg:
start2 = pos
bits[pos] = 90
pos += 1
break
pos += 1
# P3
while pos < cnt - 16*1024:
if A[pos] < avg and A[pos+1] > avg:
start3 = pos
bits[pos] = 80
pos += 1
break
pos += 1
# P4
while pos < cnt - 16*1024:
if A[pos] < avg and A[pos+1] > avg:
start4 = pos
bits[pos] = 70
pos += 1
break
pos += 1
sig_diff = start4 - start1
if 20 < sig_diff < 25:
bits[msg_start] = 500
bit_len = int((start4 - start1) / 4.5)
# print(pos, start1, start4, ' - ', bit_len)
# start = start1 + 8*bit_len
parse_message(A, msg_start, bit_len)
pos += 450
# For debugging: check signal start
# plt.plot(A)
# plt.plot(bits)
# plt.show()
I hope it was useful, thanks for reading.