В асинхронной науке центральное место занимает свойство схем, называемое независимостью от скорости, по английски speed independent (далее SI). Считается, что это свойство является аналогом независимости асинхронных схем от задержек логических элементов. Неудивительно, что термин SI упоминается практически в каждой работе по асинхронике. Но периодически по части этого термина возникают какие-то смутные сомнения. Не случайно, что все чаще этот термин заменяется другим термином, именуемом самосинхронностью. Прояснить эту ситуацию поможет обращение к первоисточнику. Речь идет о втором томе книги Р. Миллера «Теория переключательных схем», а если точнее, о главе 10, именуемой «Теория переключательных схем, не зависящих от скорости».
Итак, вот определение схем, не зависящих от скорости.

Класс (эквивалентности) это полное множество допустимых состояний схемы такое, что для любого состояния из этого множества существует последовательность допустимых состояний, начинающаяся с данного состояния и содержащая все состояния данного множества. Иными словами, из любого состояния класса можно попасть в любое же состояние того же класса.
Класс (эквивалентности) является заключительным, если из состояний данного класса нельзя перейти в состояние, принадлежащее иному классу.
К примеру, все живые схемы (поведения) являются, не зависящими от скорости. Также не зависят от скорости схемы, которые в итоге обязательно останавливаются, причем в единственном состоянии.
Далее автор устанавливает связь между SI схемами с одной стороны, и с полумодулярными, последовательными, дистрибутивными схемами с другой стороны. И в заключение приводит перечень замечательных свойств схем, не зависящих от скорости.

Особенно интересен первый пункт. В нем как раз и говорится о том, что схемы, независящие от скорости, не зависят от задержек логических элементов. К сожалению в тексте не приведены в явном виде основания для данного вывода. Возможно в этом и есть причина последующих недоразумений по поводу термина SI. В действительности же этот вывод совершенно справедлив. В начале 10 главы автором приводятся правила вычисления последующих состояний.

Переход схемы в следующее состояние является следствием переключения выхода какого-то логического элемента (или выходов нескольких элементов). То есть промежуток времени между созданием условий для переключения логического элемента (возбуждением) и самим его переключением ничем не ограничен. А таковой промежуток времени и является задержкой логического элемента. То есть с самого начала автор исходит из предположения, что задержки логических элементов могут быть сколь угодно велики. Действительно, чуть дальше написано следующее.

Ну и, чтоб рассеять все сомнения, цитата с первой страницы 10 главы.

Таким образом установлен непреложный факт: независимость от задержек логических элементов является не свойством схемы, а свойством модели, в которой данная схема исследуется. То есть любая схема, SI или же не SI, исследованная таким же образом, как это описывает Р.Миллер, является не зависящей от задержек логических элементов. В то же время любая схема может быть исследована в модели с ограниченной задержкой. В такой модели множество допустимых состояний является подмножеством множества допустимых состояний при рассмотрении той же схемы в модели с неограниченной задержкой элементов. При исследовании схемы в модели с ограниченной задержкой элементов, схема может быть не зависящей от скорости и в то же время зависеть от задержек элементов.
Таким образом выясняется, что независимость схемы от задержек логических элементов никак не связана со свойством SI. Тогда встает вопрос: а в чем смысл введения определения независимости от скорости? Действительно, рассмотрим две схемы и их поведения.
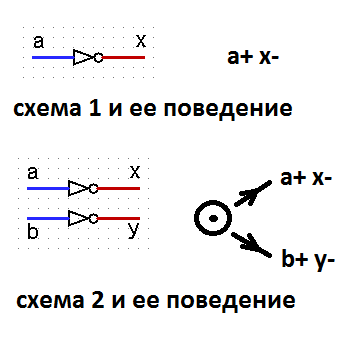
Сигналы a, b для обоих схем входные, сигналы x, y — выходные. Обе схемы реализуют совершенно разумные поведения. Но при этом схема 1 не зависит от скорости, а схема 2 таковым свойством не обладает. Да, можно говорить, что определение SI введено без разделения сигналов на входные и выходные. Но такое разделение сигналов автором подразумевалось, и об этом есть замечание в тексте.
Осмысленность и разумность введения определения свойства SI выявляется только в связи со свойством полумодулярности. Для схем, обладающих свойством полумодулярности, каждый сигнал может снять свое возбуждение не иначе как посредством своего переключения. Не полумодулярные схемы при физической реализации череваты глитчами и метастабильными состояниями. Только полумодулярные схемы могут считаться устойчивыми.
Но связь между свойствами полумодулярности и независимости от скорости односторонняя. То есть полумодулярные схемы не зависят от скорости, но обратное не верно. SI схемы могут быть не полумодулярными. То есть действительно важное свойство, делящее схемы по признаку устойчивости, это полумодулярность. При этом важно понимать, что полумодулярные схемы также могут зависеть от задержек логических элементов, если рассматривать их в модели с ограниченной задержкой.
Но и это еще не все. Свойство полумодулярности также определено для автономных схем, то есть без разделения сигналов на входные и выходные. Из-за этого схемы (поведения) со свободным выбором не отвечают критериям полумодулярности. А между тем эти схемы могут быть такими же устойчивыми, как и полумодулярные. К примеру, вышеприведенная схема 2 не является полумодулярной, но в плане устойчивости она ничем не уступает схеме 1, которая полумодулярной является.
Выход из данного тупика есть. В книге J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno, A. Yakovlev «Logic Synthesis for Asynchronous Controllers and Interfaces» дано определение свойства output persistency (OP).
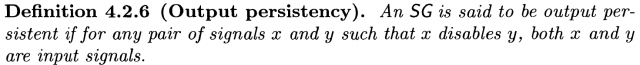
Именно свойство OP является актуальным свойством, разделяющим схемы (поведения) на устойчивые и не устойчивые. Именно свойство OP должно занять место свойства SI. При этом не следует забывать, что независимость от задержек логических элементов это свойство модели, в которой исследуются схемы (поведения). И OP схемы также могут зависеть от задержек элементов, если рассматриваются в модели с ограниченной задержкой.
Несмотря на всю предыдущую критику, к Р. Миллеру претензий нет. В его работе логических ошибок нет. Вина за более чем полувековое заблуждение лежит скорее на читателях, неверно трактовавших работу Р. Миллера.
Ну и наконец приятный вывод из вышеизложенного. В модель описания поведений STG заложена неограниченная задержка логических элементов. Правила изменения маркировки, извлечения таблицы истинности сформулированы из предположения о неограниченности задержки элементов. Следовательно любая схема, полученная путем вычисления логических функций по STG (либо с помощью таблицы истинности, либо непосредственно по графу), заведомо является не зависящей от задержек логических элементов. Правда надо понимать, что дальнейшие манипуляции с полученной схемой могут привести к потере этого ценного качества.
Итак, вот определение схем, не зависящих от скорости.

Класс (эквивалентности) это полное множество допустимых состояний схемы такое, что для любого состояния из этого множества существует последовательность допустимых состояний, начинающаяся с данного состояния и содержащая все состояния данного множества. Иными словами, из любого состояния класса можно попасть в любое же состояние того же класса.
Класс (эквивалентности) является заключительным, если из состояний данного класса нельзя перейти в состояние, принадлежащее иному классу.
К примеру, все живые схемы (поведения) являются, не зависящими от скорости. Также не зависят от скорости схемы, которые в итоге обязательно останавливаются, причем в единственном состоянии.
Далее автор устанавливает связь между SI схемами с одной стороны, и с полумодулярными, последовательными, дистрибутивными схемами с другой стороны. И в заключение приводит перечень замечательных свойств схем, не зависящих от скорости.

Особенно интересен первый пункт. В нем как раз и говорится о том, что схемы, независящие от скорости, не зависят от задержек логических элементов. К сожалению в тексте не приведены в явном виде основания для данного вывода. Возможно в этом и есть причина последующих недоразумений по поводу термина SI. В действительности же этот вывод совершенно справедлив. В начале 10 главы автором приводятся правила вычисления последующих состояний.

Переход схемы в следующее состояние является следствием переключения выхода какого-то логического элемента (или выходов нескольких элементов). То есть промежуток времени между созданием условий для переключения логического элемента (возбуждением) и самим его переключением ничем не ограничен. А таковой промежуток времени и является задержкой логического элемента. То есть с самого начала автор исходит из предположения, что задержки логических элементов могут быть сколь угодно велики. Действительно, чуть дальше написано следующее.

Ну и, чтоб рассеять все сомнения, цитата с первой страницы 10 главы.

Таким образом установлен непреложный факт: независимость от задержек логических элементов является не свойством схемы, а свойством модели, в которой данная схема исследуется. То есть любая схема, SI или же не SI, исследованная таким же образом, как это описывает Р.Миллер, является не зависящей от задержек логических элементов. В то же время любая схема может быть исследована в модели с ограниченной задержкой. В такой модели множество допустимых состояний является подмножеством множества допустимых состояний при рассмотрении той же схемы в модели с неограниченной задержкой элементов. При исследовании схемы в модели с ограниченной задержкой элементов, схема может быть не зависящей от скорости и в то же время зависеть от задержек элементов.
Таким образом выясняется, что независимость схемы от задержек логических элементов никак не связана со свойством SI. Тогда встает вопрос: а в чем смысл введения определения независимости от скорости? Действительно, рассмотрим две схемы и их поведения.

Сигналы a, b для обоих схем входные, сигналы x, y — выходные. Обе схемы реализуют совершенно разумные поведения. Но при этом схема 1 не зависит от скорости, а схема 2 таковым свойством не обладает. Да, можно говорить, что определение SI введено без разделения сигналов на входные и выходные. Но такое разделение сигналов автором подразумевалось, и об этом есть замечание в тексте.
Осмысленность и разумность введения определения свойства SI выявляется только в связи со свойством полумодулярности. Для схем, обладающих свойством полумодулярности, каждый сигнал может снять свое возбуждение не иначе как посредством своего переключения. Не полумодулярные схемы при физической реализации череваты глитчами и метастабильными состояниями. Только полумодулярные схемы могут считаться устойчивыми.
Но связь между свойствами полумодулярности и независимости от скорости односторонняя. То есть полумодулярные схемы не зависят от скорости, но обратное не верно. SI схемы могут быть не полумодулярными. То есть действительно важное свойство, делящее схемы по признаку устойчивости, это полумодулярность. При этом важно понимать, что полумодулярные схемы также могут зависеть от задержек логических элементов, если рассматривать их в модели с ограниченной задержкой.
Но и это еще не все. Свойство полумодулярности также определено для автономных схем, то есть без разделения сигналов на входные и выходные. Из-за этого схемы (поведения) со свободным выбором не отвечают критериям полумодулярности. А между тем эти схемы могут быть такими же устойчивыми, как и полумодулярные. К примеру, вышеприведенная схема 2 не является полумодулярной, но в плане устойчивости она ничем не уступает схеме 1, которая полумодулярной является.
Выход из данного тупика есть. В книге J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno, A. Yakovlev «Logic Synthesis for Asynchronous Controllers and Interfaces» дано определение свойства output persistency (OP).
Именно свойство OP является актуальным свойством, разделяющим схемы (поведения) на устойчивые и не устойчивые. Именно свойство OP должно занять место свойства SI. При этом не следует забывать, что независимость от задержек логических элементов это свойство модели, в которой исследуются схемы (поведения). И OP схемы также могут зависеть от задержек элементов, если рассматриваются в модели с ограниченной задержкой.
Несмотря на всю предыдущую критику, к Р. Миллеру претензий нет. В его работе логических ошибок нет. Вина за более чем полувековое заблуждение лежит скорее на читателях, неверно трактовавших работу Р. Миллера.
Ну и наконец приятный вывод из вышеизложенного. В модель описания поведений STG заложена неограниченная задержка логических элементов. Правила изменения маркировки, извлечения таблицы истинности сформулированы из предположения о неограниченности задержки элементов. Следовательно любая схема, полученная путем вычисления логических функций по STG (либо с помощью таблицы истинности, либо непосредственно по графу), заведомо является не зависящей от задержек логических элементов. Правда надо понимать, что дальнейшие манипуляции с полученной схемой могут привести к потере этого ценного качества.