
В работе предлагается новый метод кластерного анализа. Его преимущество в менее сложном с вычислительной точки зрения алгоритме. Метод основан на расчете голосов за то, что пара объектов находится в одном классе из информации о значении отдельных координат.
Введение
Большой потребностью анализа данных является разработка эффективных методов классификации. В таких методах требуется разделить все множество объектов на оптимальное число классов, основываясь только на информации о значении отдельных показателей [Загоруйко 1999].
Кластерный анализ являются одним из самых популярных методов анализа данных и математической статистики. Кластерный анализ позволяет автоматически найти классы объектов, используя только информацию о количественных показателях объектов (обучение без учителя). Каждый такой класс может задаваться одним самым характерным для него объектом, например средним по показателям. Существует большое число методов и подходов для классификации данных.
Современные исследования в области кластерного анализа проводятся с целью улучшения методов для определения классов сложной топологии [Furaoa 2007, Загоруйко 2013], а также для улучшения скорости работы алгоритмов в случае больших данных.
В данной работе предлагается метод классификации основанный, на получении голосов за то, что пара объектов находится в одном классе, основываясь на информации о значении отдельных показателей. Предлагается считать, что пара объектов находится в одном классе, если значения их отдельных показателей находятся в интервале с длиной не превосходящей заданную величину.
Метод k-средних
Метод k-средних является одним из наиболее популярных методов кластеризации. Его целью является получение таких центров данных, которые бы соответствовали бы гипотезе компактности классов данных при их симметричном радиальном распределении. Одним из способов определить положения таких центров, при заданном их количестве \textit{k}, является EM подход.
В данном методе выполняется последовательно две процедуры.
- Определение для каждого объекта данных
ближайшего центра
, и назначение данному объекту метки класса
. Далее для всех объектов становится определена их принадлежность различным классам.
- Вычисление нового положения центров всех классов.
Итеративно повторяя эти две процедуры из начального случайного положения центров \textit{k} классов, можно добиться разделения объектов на классы, которые бы максимально бы соответствовали гипотезе радиальной компактности классов.
С методом k-средних будет сравниваться новый авторский алгоритм классификации.
Новый метод
Новый алгоритм кластерного анализа построен на базе голосов за принадлежность различным кластерам из информации о значений отдельных координат точек данных.
- Задается величина d, характеризующая длину интервала показателей, в пределах которого два объекта считаются принадлежащими одному классу.
- Выбирается показатель
и рассматриваются все пары объектов
, где
.
- Если
, то величине
(прибавляется голос).
- Действия 2) и 3) повторяются для всех показателей
.
- Задается величина p, характеризующая минимальное количество голосов, за принадлежность одинаковым классам.
- Методом ключей пар значений определяются все классы объектов, таких что в пределах одного класса голоса за пары объектов из этих классов >=p.
- Перебираются все значения d и p и повторяются пункты 1) — 6) для получения количества классов ближайшее к заданному числу классов g.
Чтобы снизить сложность алгоритма до N, можно использовать T интервалов для отдельных показателей и пункт 2) и 3) в алгоритме заменить на следующие:
1. Выбирается показатель
2. Если
Численный эксперимент
В качестве исходных данных были взяты данные, с интуитивно понятной человеку классификацией.
На рисунках 1 и 2 приведены результаты классификации метода k-средних и нового метода классификации.
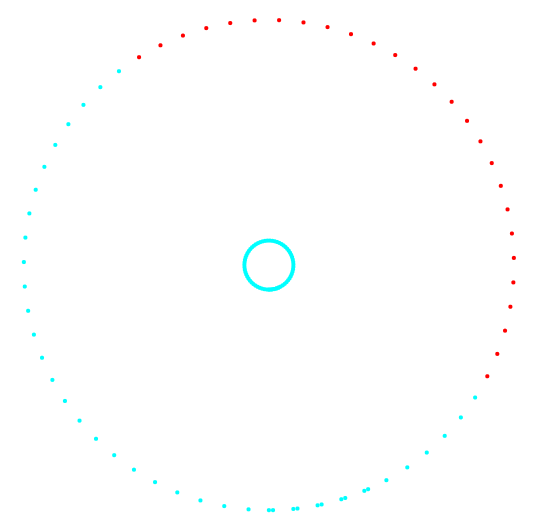

Рис. 1. Проекция 1-2 и классификация данных.
Слева метод k-средних, справа авторский метод.


Рис. 2. Проекция 2-3 и классификация данных.
Слева метод k-средних, справа авторский метод.
По результату сравнения двух методов, видно очевидное преимущество авторского метода, в его способности обнаружения кластеров сложной топологии.
Программная реализация
Метод кластеризации k-средних был реализован программно как web приложение. Вычислительная часть приложения вынесена на сервер написанном на языке PHP c использованием фреймворка Zend. Интерфейс приложения написан с использованием HTML, CSS, JavaScript, JQuery. Приложение доступно по адресу http://svlaboratory.org/application/klaster2 после регистрации нового пользователя. Приложение позволяет визуализировать принадлежность объектов различным кластерам в заданной плоскости координат.
Заключение
Предложен новый метод классификации. Преимущества данного метода в распознании классов сложной топологии, не радиального распределения, а также в меньшей сложности алгоритма и меньшем количестве действий, что особенно выгодно в случае больших массивов данных.
Список литературы (References)
- Загоруйко Н.Г. Прикладные методы анализа данных и знаний. Новосибирск: Изд-во Ин-та математики, 1999. 270 с.
- Загоруйко Н.Г., Борисова И.А., Кутненко О.А., Леванов Д.А. Обнаружение закономерностей в массивах экспериментальных данных // Вычислительные технологии. − 2013. Т. 18. № S1. С. 12-20.
- Shen Furaoa, Tomotaka Ogurab, Osamu Hasegawab An enhanced self-organizing incremental neural network for online unsupervised learning. Hasegawa Lab, 2007.