Продолжаю публикацию своих лекций, изначально предназначенных для студентов, учащихся по специальности «цифровая геология». На хабре это уже третья публикация из цикла, первая статья была вводной, она необязательна к прочтению. Однако же для понимания этой статьи необходимо прочитать введение в системы линейных уравнений даже в том случае, если вы знаете, что это такое, так как я буду много ссылаться на примеры из этого введения.
Итак, задача на сегодня: научиться простейшей обработке геометрии, чтобы, например, суметь преобразовать мою голову в истукана с острова Пасхи:

Текущий план лекций:
Официальный репозиторий курса живёт здесь. Книга ещё не окончена, я потихоньку компилирую воедино статьи, опубликованные на Хабре.
В рамках этой статьи моим основным инструментом будет поиск минимума квадратичных функций; но, прежде чем мы начнём этим инструментом пользоваться, нужно хотя бы понять, где у него кнопка вкл/выкл. Для начала освежим память и вспомним, что такое матрицы, что такое положительное число, а также что такое производная.
В этом тексте я буду обильно пользоваться матричными обозначениями, так что давайте вспоминать, что это такое. Не подглядывайте дальше по тексту, сделайте паузу на несколько секунд, и попробуйте сформулировать, что такое матрица.
Ответ очень простой. Матрица это просто шкафчик, в котором хранятся хреновины. Каждая хреновина лежит в своей ячейке, ячейки группируются рядами в строки и столбцы. В нашем конкретном случае хреновинами будут обычные вещественные числа; для программиста проще всего представлять матрицу как нечто навроде
как нечто навроде
Зачем же такие хранилища нужны? Что они описывают? Может быть, я вас расстрою, но сама по себе матрица не описывает ничего, она хранит. Например, в ней можно хранить коэффициенты всяких функций. Давайте на секунду забудем про матрицы, и представим, что у нас есть число . Что оно означает? Да чёрт его знает… Например, это может быть коэффициент внутри функции, которая на вход берёт одно число, и на выход даёт другое число:
. Что оно означает? Да чёрт его знает… Например, это может быть коэффициент внутри функции, которая на вход берёт одно число, и на выход даёт другое число:
Одну версию такой функции математик мог бы записать как
Ну а в мире программистов она бы выглядела следующим образом:
С другой стороны, а почему такая функция, а не совсем другая? Давайте возьмём другую!
Раз уж я начал про программистов, я обязан записать её код :)
Одна из этих функций линейная, а вторая квадратичная. Какая из них правильная? Да никакая, само по себе число не определяет этого, оно просто хранит какое-то значение! Какую вам надо функцию, такую и стройте.
не определяет этого, оно просто хранит какое-то значение! Какую вам надо функцию, такую и стройте.
То же самое происходит и с матрицами, это хранилища, нужные на случай, когда одиночных чисел (скаляров) не хватает, своего рода расширение чисел. Над матрицами, ровно как и над числами, определены операции сложения и умножения.
Давайте представим, что у нас есть матрица , например, размера 2x2:
, например, размера 2x2:
Эта матрица сама по себе ничего не значит, например, она может быть интерпретирована как функция
Эта функция преобразует двумерный вектор в двумерный вектор. Графически это удобно представлять как преобразование изображения: на вход даём изображение, а на выходе получаем его растянутую и/или повёрнутую (возможно даже зеркально отражённую!) версию. Очень скоро я приведу картинку с различными примерами такой интерпретации матриц.
А можно матрицу представлять себе как функцию, которая двумерный вектор преобразует в скаляр:
представлять себе как функцию, которая двумерный вектор преобразует в скаляр:
Обратите внимание, что с векторами возведение в степень не очень-то определено, поэтому я не могу написать , как писал в случае с обычными числами. Очень рекомендую тем, кто не привык с лёгкостью жонглировать матричными умножениями, ещё раз вспомнить правило умножения матриц, и проверить, что выражение
, как писал в случае с обычными числами. Очень рекомендую тем, кто не привык с лёгкостью жонглировать матричными умножениями, ещё раз вспомнить правило умножения матриц, и проверить, что выражение  вообще разрешено и действительно даёт скаляр на выходе. Для этого можно, например, явно поставить скобки
вообще разрешено и действительно даёт скаляр на выходе. Для этого можно, например, явно поставить скобки  . Напоминаю, что у нас
. Напоминаю, что у нас  — вектор размерности 2 (сохранённый в матрице размерности 2x1), выпишем явно все размерности:
— вектор размерности 2 (сохранённый в матрице размерности 2x1), выпишем явно все размерности:
Возвращаясь в тёплый и пушистый мир программистов, мы можем записать эту же квадратичную функцию как-то так:
Теперь я задам очень глупый вопрос: что такое положительное число? У нас есть отличный инструмент, называется предикат больше . Но не торопитесь отвечать, что число
. Но не торопитесь отвечать, что число  положительно тогда и только тогда, когда
положительно тогда и только тогда, когда  , это было бы слишком просто. Давайте определим положительность следущим образом:
, это было бы слишком просто. Давайте определим положительность следущим образом:
Число положительно тогда и только тогда, когда для всех ненулевых вещественных
положительно тогда и только тогда, когда для всех ненулевых вещественных  выполняется условие
выполняется условие  .
.
Выглядит довольно мудрёно, но зато отлично применяется к матрицам:
Квадратная матрица называется положительно определённой, если для любых ненулевых
называется положительно определённой, если для любых ненулевых  выполняется условие
выполняется условие  , то есть, соответствующая квадратичная форма строго положительна везде, кроме начала координат.
, то есть, соответствующая квадратичная форма строго положительна везде, кроме начала координат.
Для чего мне нужна положительность? Как я уже упоминал в начале статьи, моим основным инструментом будет поиск минимумов квадратичных функций. А ведь для того, чтобы минимум искать, было бы недурно, если бы он существовал! Например, у функции минимума очевидно не существует, посколькуо число -1 не является положительным, и
минимума очевидно не существует, посколькуо число -1 не является положительным, и  бесконечно убывает с ростом
бесконечно убывает с ростом  : ветви параболы
: ветви параболы  смотрят вниз. Положительно определённые матрицы хороши тем, что соответствующие квадратичные формы образуют параболоид, имеющие (единственный) минимум. Следующая иллюстрация показывает семь различных примеров матриц
смотрят вниз. Положительно определённые матрицы хороши тем, что соответствующие квадратичные формы образуют параболоид, имеющие (единственный) минимум. Следующая иллюстрация показывает семь различных примеров матриц  , как положительно определённых и симметричных, так и не очень. Верхний ряд: интерпретация матриц как функций
, как положительно определённых и симметричных, так и не очень. Верхний ряд: интерпретация матриц как функций  . Средний ряд: интерпретация матриц как функций
. Средний ряд: интерпретация матриц как функций  .
.
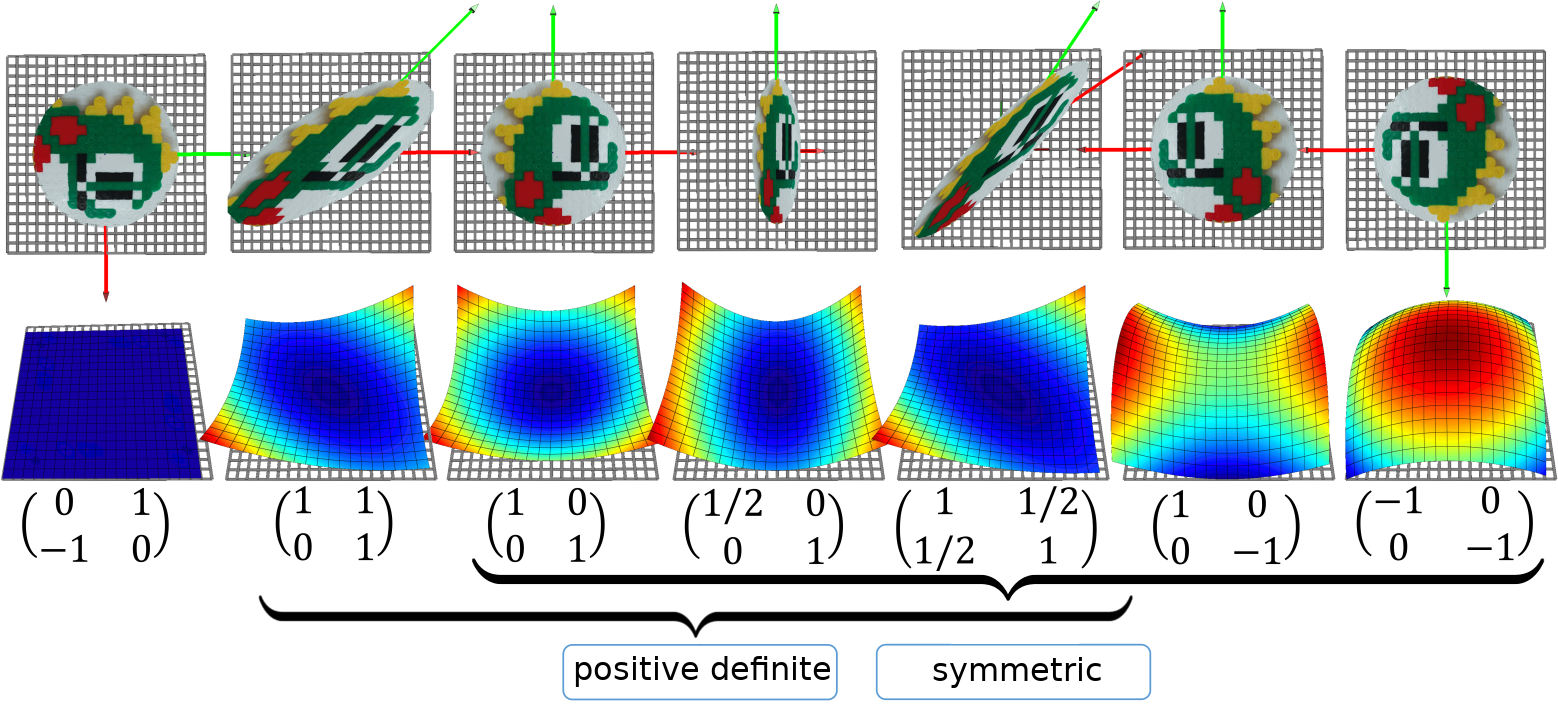
Таким образом, я буду работать с положительно определёнными матрицами, которые являются обобщением положительных чисел. Более того, конкретно в моём случае матрицы будут ещё и симметричными! Любопытно, что довольно часто, когда люди говорят про положительную определённость, они подразумевают ещё и симметричность, что может быть косвенно объяснено следующим (необязательным для понимания последующего текста) наблюдением.
Давайте рассмотрим квадратичную форму для произвольной матрицы
для произвольной матрицы  ; затем к
; затем к  добавим и сразу же отнимем половину её транспонированной версии:
добавим и сразу же отнимем половину её транспонированной версии:
Матрица симметрична:
симметрична:  ; матрица
; матрица  антисимметрична:
антисимметрична:  . Примечательным фактом является то, что для любой антисимметричной матрицы соответствующая квадратичная форма тождественно равна нулю. Это вытекает из следующего наблюдения:
. Примечательным фактом является то, что для любой антисимметричной матрицы соответствующая квадратичная форма тождественно равна нулю. Это вытекает из следующего наблюдения:
То есть, квадратичная форма одновременно равна
одновременно равна  и
и  , что возможно только в том случае, когда
, что возможно только в том случае, когда  . Из этого факта вытекает то, что для произвольной матрицы
. Из этого факта вытекает то, что для произвольной матрицы  соответствующая квадратичная форма
соответствующая квадратичная форма  может быть выражена и через симметричную матрицу
может быть выражена и через симметричную матрицу  :
:
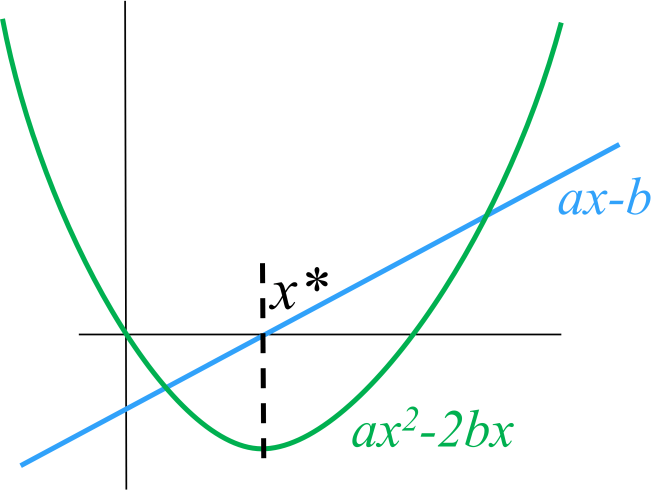
Вернёмся ненадолго в одномерный мир; я хочу найти минимум функции . Число
. Число  положительно, поэтому минимум существует; чтобы его найти, приравняем нулю соответствующую производную:
положительно, поэтому минимум существует; чтобы его найти, приравняем нулю соответствующую производную:  . Продифференцировать одномерную квадратичную функцию труда не составляет:
. Продифференцировать одномерную квадратичную функцию труда не составляет:  ; поэтому наша проблема сводится к решению уравнения
; поэтому наша проблема сводится к решению уравнения  , откуда путём страшных усилий получам решение
, откуда путём страшных усилий получам решение  . Следующий рисунок иллюстрирует эквивалентность двух проблем: решение
. Следующий рисунок иллюстрирует эквивалентность двух проблем: решение  уравнения
уравнения  совпадает с решением уравнения
совпадает с решением уравнения  .
.
Я клоню к тому, что нашей глобальной целью является минимизация квадратичных функций, мы же про наименьшие квадраты говорим. Но при этом что мы действительно умеем делать хорошо, так это решать линейные уравнения (и системы линейных уравнений). И очень здорово, что одно эквивалентно другому!
Единственное, что нам осталось, так это убедиться, что эта эквивалентность в одномерном мире распространяется и на случай переменных. Чтобы это проверить, для начала докажем три теоремы.
переменных. Чтобы это проверить, для начала докажем три теоремы.
Первая теорема гласит о том, что матрицы инварианты относительно транспонирования:
инварианты относительно транспонирования:

Доказательство настолько сложное, что для краткости я вынужден его опустить, но попробуйте найти его самостоятельно.
Вторая теорема позволяет дифференцировать линейные функции. В случае вещественной функции одной переменной мы знаем, что , но что происходит в случае вещественной функции
, но что происходит в случае вещественной функции  переменных?
переменных?

То есть, никаких сюрпризов, просто матричная запись того же самого школьного результата. Доказательство крайне прямолинейное, достаточно просто записать определение градиента:
Применив первую теорему , мы завершаем доказательство.
, мы завершаем доказательство.
Теперь переходим к квадратичным формам. Мы знаем, что в случае вещественной функции одной переменной , а что будет в случае квадратичной формы?
, а что будет в случае квадратичной формы?

Кстати, обратите внимание, что если матрица симметрична, то теорема гласит, что
симметрична, то теорема гласит, что  .
.
Это доказательство тоже прямолинейно, просто запишем квадратичную форму как двойную сумму:
А затем посмотрим, чему равна частная производная этой двойной суммы по переменной :
:
\begin{align*}
\frac{\partial (x^\top A x)}{\partial x_i}
&= \frac{\partial}{\partial x_i} \left(\sum\limits_{k_1}\sum\limits_{k_2} a_{k_1 k_2} x_{k_1} x_{k_2}\right) = \\
&= \frac{\partial}{\partial x_i} \left(
\underbrace{\sum\limits_{k_1\neq i}\sum\limits_{k_2\neq i} a_{ik_2}x_{k_1} x_{k_2}}_{k_1 \neq i, k_2 \neq i}+\underbrace{\sum\limits_{k_2\neq i} a_{ik_2}x_i x_{k_2}}_{k_1 = i, k_2\neq i}+
\underbrace{\sum\limits_{k_1\neq i} a_{k_1 i} x_{k_1} x_i}_{k_1 \neq i, k_2 = i}+
\underbrace{a_{ii}x_i^2}_{k_1 = i, k_2 = i}\right) = \\
& = \sum\limits_{k_2\neq i} a_{ik_2}x_{k_2} + \sum\limits_{k_1\neq i} a_{k_1 i} x_{k_1} + 2 a_{ii} x_i = \\
& = \sum\limits_{k_2} a_{ik_2}x_{k_2} + \sum\limits_{k_1} a_{k_1 i} x_{k_1} = \\
& = \sum\limits_{j} (a_{ij} + a_{ji}) x_j \\
\end{align*}
Я разбил двойную сумму на четыре случая, которые выделены фигурными скобками. Каждый из этих четырёх случаев дифференцируется тривиально. Осталось сделать последнее действие, собрать частные производные в вектор градиента:
Давайте не забывать направление движения. Мы видели, что при положительном числе в случае вещественных функций одной перменной решить уравнение
в случае вещественных функций одной перменной решить уравнение  или минимизировать квадратичную функцию
или минимизировать квадратичную функцию  — это одно и то же.
— это одно и то же.
Мы хотим показать соответствующую связь в случае симметричной положительно определённой матрицы .
.
Итак, мы хотим найти минимум квадратичной функции
Ровно как и в школе, приравняем нулю производную:
Оператор Гамильтона линеен, поэтому мы можем переписать наше уравнение в следующем виде:
Теперь применим вторую и третью теоремы о дифференцировании:
Вспомним, что симметрична, и поделим уравнение на два, получаем нужную нам систему линейных уравнений:
симметрична, и поделим уравнение на два, получаем нужную нам систему линейных уравнений:
Ура-ура, перейдя от одной переменной к многим, мы не потеряли ровным счётом ничего, и можем эффективно минимизировать квадратичные функции!
Наконец мы можем перейти к основному содержанию этой лекции. Представьте, что у нас есть две точки на плоскости и
и  , и мы хотим найти уравнение прямой, проходящей через эти две точки. Уравнение прямой можно записать в виде
, и мы хотим найти уравнение прямой, проходящей через эти две точки. Уравнение прямой можно записать в виде  , то есть, наша задача это найти коэффициенты
, то есть, наша задача это найти коэффициенты  и
и  . Это упражнение для седьмого-восьмого класса школы, запишем систему уравнений:
. Это упражнение для седьмого-восьмого класса школы, запишем систему уравнений:
У нас два уравнения с двумя неизвестными ( и
и  ), остальное известно.
), остальное известно.
В общем случае решение существует и единственно. Для удобства перепишем ту же самую систему в матричном виде:
Получим уравнение типа , которое тривиально решается
, которое тривиально решается  .
.
А теперь представим, что у нас есть три точки, через которые нужно провести прямую:
В матричном виде эта система запишется следующим образом:
Теперь у нас матрица прямоугольная, и у неё просто не существует обратной! Это совершенно нормально, так как у нас всего две переменных и три уравнения, и в общем случае эта система не имеет решения. Это соверешенно нормальная ситуация в реальном мире, когда точки — это данные зашумлённых измерений, и нам нужно найти параметры
прямоугольная, и у неё просто не существует обратной! Это совершенно нормально, так как у нас всего две переменных и три уравнения, и в общем случае эта система не имеет решения. Это соверешенно нормальная ситуация в реальном мире, когда точки — это данные зашумлённых измерений, и нам нужно найти параметры  и
и  , которые наилучшим образом приближают данные измерений. Мы этот пример уже рассматривали в первой лекции, когда калибровали безмен. Но тогда у нас решение было чисто алгебраическим и очень громоздким. Давайте попробуем более интуитивный способ.
, которые наилучшим образом приближают данные измерений. Мы этот пример уже рассматривали в первой лекции, когда калибровали безмен. Но тогда у нас решение было чисто алгебраическим и очень громоздким. Давайте попробуем более интуитивный способ.
Нашу систему можно записать в следующем виде:
Или, более кратко,
Векторы ,
,  и
и  известны, нужно найти скаляры
известны, нужно найти скаляры  и
и  .
.
Очевидно, что линейная комбинация порождает плоскость, и если вектор
порождает плоскость, и если вектор  в этой плоскости не лежит, то точного решения не существует; однако же мы ищем приближённое решение.
в этой плоскости не лежит, то точного решения не существует; однако же мы ищем приближённое решение.
Давайте определим ошибку решения как . Нашей зачей является найти такие значения параметров
. Нашей зачей является найти такие значения параметров  и
и  , которые минимизируют длину вектора
, которые минимизируют длину вектора  . Иначе говоря, проблема записывается как
. Иначе говоря, проблема записывается как  .
.
Вот иллюстрация:.

Имея заданные векторы ,
,  и
и  , мы стараемся минимизировать длину вектора ошибки
, мы стараемся минимизировать длину вектора ошибки  . Очевидно, что его длина минимизируется, если он перпендикулярен плоскости, натянутой на векторы
. Очевидно, что его длина минимизируется, если он перпендикулярен плоскости, натянутой на векторы  и
и  .
.
Но постойте, где же наименьшие квадраты? Сейчас будут. Функция извлечения корня монотонна, поэтому
монотонна, поэтому  =
=  !
!
Вполне очевидно, что длина вектора ошибки минимизируется, если он перпендикулярен плоскости, натянутой на векторы и
и  , что можно записать, приравняв нулю соответствующие скалярные произведения:
, что можно записать, приравняв нулю соответствующие скалярные произведения:
В матричном виде эту же самую систему можно записать как
или же
Но мы на этом не остановимся, так как запись можно ещё больше сократить:
И самая последняя трансформация:
Давайте посчитаем размерности. Матрица имеет размер
имеет размер  , поэтому
, поэтому  имеет размер
имеет размер  . Матрица
. Матрица  имеет размер
имеет размер  , но вектор
, но вектор  имеет размер
имеет размер  . То есть, в общем случае матрица
. То есть, в общем случае матрица  обратима! Более того,
обратима! Более того,  имеет ещё пару приятных свойств.
имеет ещё пару приятных свойств.
 симметрична.
симметрична.
Это совсем нетрудно показать:
 положительно полуопределена:
положительно полуопределена: 
Это следует из того факта, что .
.
Кроме того, положительно определена в том случае, если
положительно определена в том случае, если  имеет линейно независимые столбцы (ранг
имеет линейно независимые столбцы (ранг  равен количеству переменных в системе).
равен количеству переменных в системе).
Итого, для системы с двумя неизвестными мы доказали, что минимизация квадратичной функции эквивалентна решению системы линейных уравнений
эквивалентна решению системы линейных уравнений  . Разумеется, всё это рассуждение применимо и к любому другому количеству переменных, но давайте ещё раз компактно запишем всё вместе простым алгебраическим подсчётом. Мы начнём с проблемы наименьших квадратов, придём к минимизации квадратичной функции знакомого нам вида, и из этого сделаем вывод об эквивалентности решению системы линейных уравнений. Итак, поехали:
. Разумеется, всё это рассуждение применимо и к любому другому количеству переменных, но давайте ещё раз компактно запишем всё вместе простым алгебраическим подсчётом. Мы начнём с проблемы наименьших квадратов, придём к минимизации квадратичной функции знакомого нам вида, и из этого сделаем вывод об эквивалентности решению системы линейных уравнений. Итак, поехали:
Таким образом, проблема наименьших квадратов эквивалентна минимизации квадратичной функции
эквивалентна минимизации квадратичной функции  с (в общем случае) симметричной положительно определённой матрицей
с (в общем случае) симметричной положительно определённой матрицей  , что, в свою очередь, эквивалентно решению системы линейных уравнений
, что, в свою очередь, эквивалентно решению системы линейных уравнений  . Уфф. Теория закончилась.
. Уфф. Теория закончилась.
Давайте вспомним один пример из предыдущей статьи:
У нас есть обычный массив x из 32 элементов, инициализированный следующим образом:
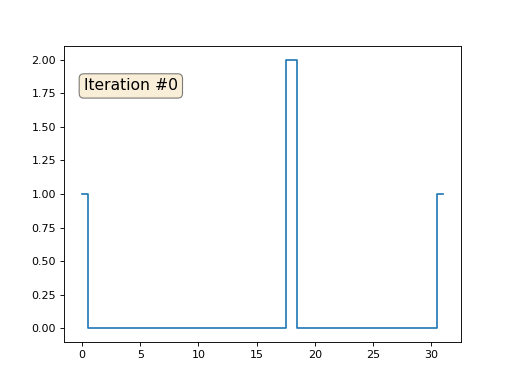
А затем мы тысячу раз выполним следующую процедуру: для каждой ячейки x[i] мы запишем в неё среднее значение соседних ячеек: x[i] = ( x[i-1] + x[i+1] )/2. Единственное исключение: мы не будем переписывать элементы массива под номерами 0, 18 и 31. Вот так выглядит эволюция массива на первых ста пятидесяти итерациях:
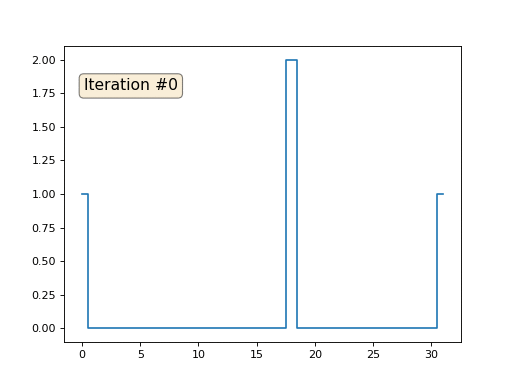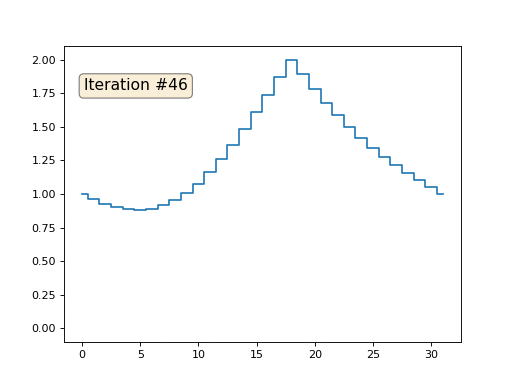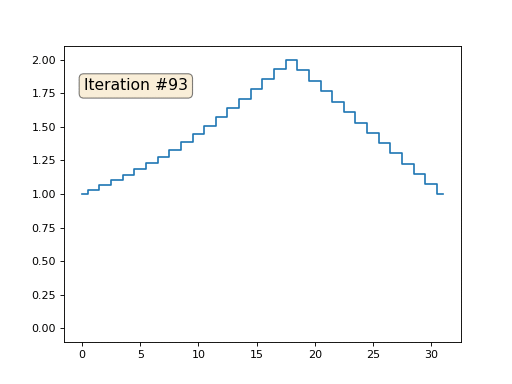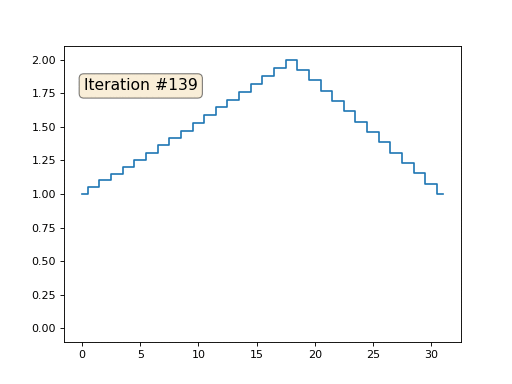
Как мы выяснили в предыдущей статье, оказывается, наш питоновский мегакод на четыре строчки решает следующиую систему линейных уравнений методом Гаусса-Зейделя:

Выяснить-то выяснили, но откуда вообще взялась эта система? Что за магия? Давайте отвлечёмся на секунду, и попробуем решить немного другую систему. У меня по-прежнему есть 32 переменных, но теперь я хочу, чтобы они все-все-все были равны одна другой. Это нетрудно записать, достаточно записать систему уравнений, которая гласит, что все соседние элементы попарно равны:
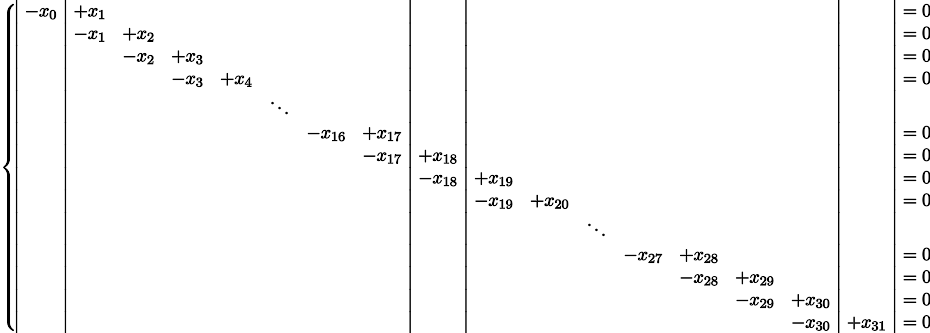
Вышеприведённый питоновский код в принципе не трогает значения трёх переменных: x0, x18, x31, поэтому давайте их перенесём в правую часть системы уравнений, т.е., исключим из множества неизвестных:
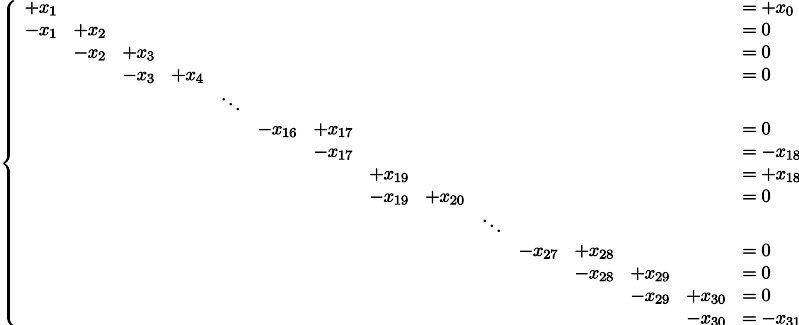
Я фиксирую начальное значение x0=1, первое уравнение говорит, что x1 = x0 = 1, второе уравнение говорит, что x2=x1=x0=1 и так далее, покуда мы не дойдём до уравнения 1 = x0 = x17 = x18 = 2. Ой. А ведь эта система не имеет решения :((
А и пофиг, мы же программисты! Давайте звать на помощь наименьшие квадраты! Наша нерешаемая система может быть записана в матричном виде ; чтобы решить нашу систему приближённо, достаточно решить систему
; чтобы решить нашу систему приближённо, достаточно решить систему  . А тут оказывается, что это ровно, один-в-один та самая система уравнений из предыдущей статьи!
. А тут оказывается, что это ровно, один-в-один та самая система уравнений из предыдущей статьи!
Интуитивно можно представлять себе процесс создания матрицы системы следующим образом: мы соединяем пружинками значения, равенства которых хотим добиться. Например, в нашем случае мы хотим, чтобы был равен
был равен  , поэтому мы добавляем уравнение
, поэтому мы добавляем уравнение  , вешая между этими значениями пружинку, которая будет их стягивать. Но поскольку значения x0, x18 и x31 жёстко зафиксированы, свободным значениям не остаётся ничего другого, как равномерно растянуть пружинки, произведя (в данном случае) кусочно-линейное решение.
, вешая между этими значениями пружинку, которая будет их стягивать. Но поскольку значения x0, x18 и x31 жёстко зафиксированы, свободным значениям не остаётся ничего другого, как равномерно растянуть пружинки, произведя (в данном случае) кусочно-линейное решение.
Давайте напишем программу, решающую эту систему уравнений. В прошлой статье мы видели, что метод Гаусса-Зейделя очень прост в программировании, но имеет очень медленную сходимость, поэтому лучше бы использовать настоящие решатели систем линейных уравнений. В самом простейшем случае, для нашего одномерного примера, код может выглядеть как-то так:
Этот код производит список x из 32 элементов, в котором хранится решение. Мы строим матрицу , строим вектор
, строим вектор  , получаем вектор с решением
, получаем вектор с решением  , а затем в этот вектор вставляем наши фиксированные значения x0=1, x18=2 и x31=1.
, а затем в этот вектор вставляем наши фиксированные значения x0=1, x18=2 и x31=1.
Этот код выполняет необходимую работу, но довольно неприятно переносить в правую часть значения фиксированных переменных. Нельзя ли схитрить? Можно! Давайте посмотрим на следующий код:
С программистской точки зрения он гораздо приятнее, вектор x получается сразу нужной размерности, да и матрицы A и b заполняются куда как проще. Но в чём же хитрость? Давайте запишем систему уравнений, которую мы решаем:

Посмотрите внимательно на последние три уравнения:
100 x0 = 100 * 1
100 x18 = 100 * 2
100 x31 = 100 * 1
Не проще ли было их записать следующим образом?
x0 = 1
x18 = 2
x31 = 1
Нет, не проще. Как я уже говорил, каждое уравнение навешивает пружинки, в данном случае пружинку между x0 и значением 1, пружинку между x18 и значением 2 и, наконец, переменная x31 тоже будет притягиваться к единице.
Но коэффициент 100 там стоит не просто так. Мы же помним, что эта система просто так не решается, мы решаем её в смысле наименьших квадратов, минимизируя соответствующую квадратичную функцию. Умножив на 100 каждый из коэффициентов последних трёх уравнений, мы вводим штраф за отклонение x0, x18 и x32 от нужных значений, в десять тысяч раз (100^2) превышающий штраф за отклонение от равенства . Грубо говоря, пружинки на последних трёх уравнениях в десять тысяч раз более жёсткие, нежели на всех остальных. Этот метод квадратичного штрафа — очень удобный инструмент введения ограничений, гораздо проще (хотя и не без недостатков), нежели редуцирование набора переменных.
. Грубо говоря, пружинки на последних трёх уравнениях в десять тысяч раз более жёсткие, нежели на всех остальных. Этот метод квадратичного штрафа — очень удобный инструмент введения ограничений, гораздо проще (хотя и не без недостатков), нежели редуцирование набора переменных.
Давайте уже перейдём к чему-нибудь более интересному, нежели сглаживание элементов одномерного массива! Для начала сделаем ровно то же самое, но на более интересных данных и с настоящим инструментарием. Я хочу взять трёхмерную поверхность, зафиксировать её границу, а всю остальную поверхность максимально сгладить:

Код доступен тут, но на всякий случай приведу полный листинг главного файла:
Я написал простейший парсер wavefront .obj файлов, поэтому моделька подгружается в одну строчку. В качестве решателя я буду использовать OpenNL, это очень мощный решатель для проблем наименьших квадратов с разреженными матрицами. Обратите внимание, что размеры матриц у нас могут быть гигантскими: например, если мы хотим получить ч/б картинку размером 1000 x 1000 пикселей, то матрица у нас будет размером миллион на миллион! Однако же на практике чаще всего подавляющее большинство элементов этой матрицы нулевые, поэтому всё не так страшно, но всё же нужно использовать специальные солверы.
у нас будет размером миллион на миллион! Однако же на практике чаще всего подавляющее большинство элементов этой матрицы нулевые, поэтому всё не так страшно, но всё же нужно использовать специальные солверы.
Итак, давайте смотреть на код. Для начала я объявляю солверу, что я хочу делать:
Я хочу иметь матрицу размером (колво вершин)x(колво вершин). Внимание, мы солверу даём матрицу
размером (колво вершин)x(колво вершин). Внимание, мы солверу даём матрицу  , а уж
, а уж  он будет строить сам, что очень удобно! Также обратите внимание на то, что я решаю не одну систему уравнений, а три последовательно для x,y и z (я соврал, что проблема трёхмерная, она по-прежнему одномерная!)
он будет строить сам, что очень удобно! Также обратите внимание на то, что я решаю не одну систему уравнений, а три последовательно для x,y и z (я соврал, что проблема трёхмерная, она по-прежнему одномерная!)
А затем я объявляю строку за строкой нашей матрицы. Для начала я фиксирую вершины, которые находятся на краю поверхности:
Можно видеть, что я использую квадратичный штраф в 100^2 для фиксирования краевых вершин.
Ну а затем для каждой пары смежных вершин я вешаю пружинку жёсткости 1 между ними:
Выполняем код и видим, как лицо сгладилось в поверхность мыльной плёнки на изогнутой проволоке. Мы сейчас только что решили проблему Дирихле, получив поверхность минимальной площади.
Давайте превратим наше лицо в гротескную маску:

В предыдущей статье я уже показывал, как это сделать на коленке, здесь же я привожу настоящий код, использующий солвер наименьших квадратов:
Полный код доступен тут. Как он работает? Как и в предыдущем примере, я начинаю с того, что фиксирую краевые вершины. Затем для каждого ребра я (тихонечко, с коэффициентом 0.2) говорю, что неплохо было бы, чтобы оно имело ровно ту же форму, что и в изначальной поверхности:
Если больше ничего не делать, и решить проблему прямо как есть, то мы на выходе должны получить ровно то, что было на входе: граница выхода равняется границе входа, плюс перепады на выходе равняются перепадам на входе.
Но мы на этом не останавливемся!
В нашу систему я добавляю ещё уравнений. Для каждой вершины я считаю кривизну поверхности вокруг неё во входной поверхности, и умножаю её на два с половиной, то есть, выходная поверхность должна иметь большую кривизну повсюду.
Затем вызываем наш решатель и получаем неплохую карикатуру.
До этого момента мы не видели ни одного нового примера, всё уже было показано в предыдущей статье. Давайте попробуем сделать что-то менее тривиальное, нежели простейшее сглаживание, которое легко можно получить, не используя никаких солверов. Код доступен тут, но давайте я приведу листинг:
Мы по-прежнему работаем с той же поверхностью, что и раньше; мы вызываем функцию snap() для каждого треугольника. Эта функция говорит, к какой оси системы координат ближе всего нормаль этого треугольника. То есть, мы хотим знать, этот треугольник скорее вертикален или горизонтален. Ну а затем мы хотим изменить геометрию нашей поверхности, чтобы то, что близко к горизонтали, стало ещё ближе! Левая часть вот этой картинки показывает результат работы функции snap():

Итак, мы раскрасили нашу поверхность в три цвета, соответствующие трём осям системы координат. Ну а затем для каждого ребра нашей системы мы добавляем следующие уравнения:
То есть, мы предписываем каждому ребру выходной поверхности походить на соответствующее ребро входной поверхности, жёсткость пружинки 1. А затем, если мы разрешаем, например, размерность x, а ребро должно быть вертикально, то просто говорим, что одна вершина равна другой с жёсткостью пружины 2:
Ну а вот и результат работы нашей программы:

Вполне резонный вопрос: истуканы с острова Пасхи, это, конечно, круто, но при чём тут геология? Есть ли примеры реальных задач?
Да, конечно. Давайте возьмём один срез земной коры:

Для геологов очень важны слои разных пород, границы (горизонты) между которыми показаны зелёным, и геологические разломы, которые показаны красным. У нас есть на вход сетка треугольников (тетраэдров в 3д) той области, которая нас интересует, но для моделирования определённых процессов необходимы квады (гексаэдры в 3д). Мы деформируем нашу модель так, чтобы разломы стали вертикальными, а горизонты (сюрприз) горизонтальными:

Затем мы просто возьмём регулярную сетку квадратов, нарежем наш домен на равномерные квадратики, и применим к ним обратное преобразование, получив необходимую сетку квадов.
Методы наименьших квадратов — мощнейший инструмент обработки данных, и применяется гораздо шире, нежели статистика в колонках экселя. Эти возможности нам открываются благодаря тому, что минимизация квадратичной функции и решение системы линейных уравнений — это одно и то же, а решать линейные уравнения мы (человечество) научились очень и очень хорошо, даже совершенно нечеловеческих размеров с миллиардами переменных.
Однако же бывают случаи, когда линейных моделей нам может не хватить. И тут на помощь могут прийти, например, нейронные сети. В следующей статье я постараюсь показать, что МНК с отбрасыванием выбросов эквивалентен одной из формулировок нейронных сетей. Оставайтесь на линии!
Итак, задача на сегодня: научиться простейшей обработке геометрии, чтобы, например, суметь преобразовать мою голову в истукана с острова Пасхи:

Текущий план лекций:
- Ликбез по теории вероятностей (статья вводная, необязательная)
- Введение в системы линейных уравнений
- Минимизация квадратичных форм и примеры задач МНК
- От наименьших квадратов к нейронным сетям
Официальный репозиторий курса живёт здесь. Книга ещё не окончена, я потихоньку компилирую воедино статьи, опубликованные на Хабре.
В рамках этой статьи моим основным инструментом будет поиск минимума квадратичных функций; но, прежде чем мы начнём этим инструментом пользоваться, нужно хотя бы понять, где у него кнопка вкл/выкл. Для начала освежим память и вспомним, что такое матрицы, что такое положительное число, а также что такое производная.
Матрицы и числа
В этом тексте я буду обильно пользоваться матричными обозначениями, так что давайте вспоминать, что это такое. Не подглядывайте дальше по тексту, сделайте паузу на несколько секунд, и попробуйте сформулировать, что такое матрица.
Различные интерпретации матриц
Ответ очень простой. Матрица это просто шкафчик, в котором хранятся хреновины. Каждая хреновина лежит в своей ячейке, ячейки группируются рядами в строки и столбцы. В нашем конкретном случае хреновинами будут обычные вещественные числа; для программиста проще всего представлять матрицу
float A[m][n];
Зачем же такие хранилища нужны? Что они описывают? Может быть, я вас расстрою, но сама по себе матрица не описывает ничего, она хранит. Например, в ней можно хранить коэффициенты всяких функций. Давайте на секунду забудем про матрицы, и представим, что у нас есть число
Одну версию такой функции математик мог бы записать как
Ну а в мире программистов она бы выглядела следующим образом:
float f(float x) {
return a*x;
}
С другой стороны, а почему такая функция, а не совсем другая? Давайте возьмём другую!
Раз уж я начал про программистов, я обязан записать её код :)
float f(float x) {
return x*a*x;
}
Одна из этих функций линейная, а вторая квадратичная. Какая из них правильная? Да никакая, само по себе число
То же самое происходит и с матрицами, это хранилища, нужные на случай, когда одиночных чисел (скаляров) не хватает, своего рода расширение чисел. Над матрицами, ровно как и над числами, определены операции сложения и умножения.
Давайте представим, что у нас есть матрица
Эта матрица сама по себе ничего не значит, например, она может быть интерпретирована как функция
vector<float> f(vector<float> x) {
return vector<float>{a11*x[0] + a12*x[1], a21*x[0] + a22*x[1]};
}
Эта функция преобразует двумерный вектор в двумерный вектор. Графически это удобно представлять как преобразование изображения: на вход даём изображение, а на выходе получаем его растянутую и/или повёрнутую (возможно даже зеркально отражённую!) версию. Очень скоро я приведу картинку с различными примерами такой интерпретации матриц.
А можно матрицу
Обратите внимание, что с векторами возведение в степень не очень-то определено, поэтому я не могу написать
Возвращаясь в тёплый и пушистый мир программистов, мы можем записать эту же квадратичную функцию как-то так:
float f(vector<float> x) {
return x[0]*a11*x[0] + x[0]*a12*x[1] + x[1]*a21*x[0] + x[1]*a22*x[1];
}
Что такое положительное число?
Теперь я задам очень глупый вопрос: что такое положительное число? У нас есть отличный инструмент, называется предикат больше
Определение 1
Число
Выглядит довольно мудрёно, но зато отлично применяется к матрицам:
Определение 2
Квадратная матрица
Для чего мне нужна положительность? Как я уже упоминал в начале статьи, моим основным инструментом будет поиск минимумов квадратичных функций. А ведь для того, чтобы минимум искать, было бы недурно, если бы он существовал! Например, у функции

Таким образом, я буду работать с положительно определёнными матрицами, которые являются обобщением положительных чисел. Более того, конкретно в моём случае матрицы будут ещё и симметричными! Любопытно, что довольно часто, когда люди говорят про положительную определённость, они подразумевают ещё и симметричность, что может быть косвенно объяснено следующим (необязательным для понимания последующего текста) наблюдением.
Лирическое отступление о симметричности матриц квадратичных форм
Давайте рассмотрим квадратичную форму
Матрица
То есть, квадратичная форма
Ищем минимум квадратичной функции
Вернёмся ненадолго в одномерный мир; я хочу найти минимум функции

Я клоню к тому, что нашей глобальной целью является минимизация квадратичных функций, мы же про наименьшие квадраты говорим. Но при этом что мы действительно умеем делать хорошо, так это решать линейные уравнения (и системы линейных уравнений). И очень здорово, что одно эквивалентно другому!
Единственное, что нам осталось, так это убедиться, что эта эквивалентность в одномерном мире распространяется и на случай
Три теоремы, или дифференцируем матричные выражения
Первая теорема гласит о том, что матрицы
Теорема 1
Доказательство настолько сложное, что для краткости я вынужден его опустить, но попробуйте найти его самостоятельно.
Вторая теорема позволяет дифференцировать линейные функции. В случае вещественной функции одной переменной мы знаем, что
Теорема 2
То есть, никаких сюрпризов, просто матричная запись того же самого школьного результата. Доказательство крайне прямолинейное, достаточно просто записать определение градиента:
Применив первую теорему
Теперь переходим к квадратичным формам. Мы знаем, что в случае вещественной функции одной переменной
Теорема 3
Кстати, обратите внимание, что если матрица
Это доказательство тоже прямолинейно, просто запишем квадратичную форму как двойную сумму:
А затем посмотрим, чему равна частная производная этой двойной суммы по переменной
\begin{align*}
\frac{\partial (x^\top A x)}{\partial x_i}
&= \frac{\partial}{\partial x_i} \left(\sum\limits_{k_1}\sum\limits_{k_2} a_{k_1 k_2} x_{k_1} x_{k_2}\right) = \\
&= \frac{\partial}{\partial x_i} \left(
\underbrace{\sum\limits_{k_1\neq i}\sum\limits_{k_2\neq i} a_{ik_2}x_{k_1} x_{k_2}}_{k_1 \neq i, k_2 \neq i}+\underbrace{\sum\limits_{k_2\neq i} a_{ik_2}x_i x_{k_2}}_{k_1 = i, k_2\neq i}+
\underbrace{\sum\limits_{k_1\neq i} a_{k_1 i} x_{k_1} x_i}_{k_1 \neq i, k_2 = i}+
\underbrace{a_{ii}x_i^2}_{k_1 = i, k_2 = i}\right) = \\
& = \sum\limits_{k_2\neq i} a_{ik_2}x_{k_2} + \sum\limits_{k_1\neq i} a_{k_1 i} x_{k_1} + 2 a_{ii} x_i = \\
& = \sum\limits_{k_2} a_{ik_2}x_{k_2} + \sum\limits_{k_1} a_{k_1 i} x_{k_1} = \\
& = \sum\limits_{j} (a_{ij} + a_{ji}) x_j \\
\end{align*}
Я разбил двойную сумму на четыре случая, которые выделены фигурными скобками. Каждый из этих четырёх случаев дифференцируется тривиально. Осталось сделать последнее действие, собрать частные производные в вектор градиента:
Минимум квадратичной функции и решение линейной системы
Давайте не забывать направление движения. Мы видели, что при положительном числе
Мы хотим показать соответствующую связь в случае симметричной положительно определённой матрицы
Итак, мы хотим найти минимум квадратичной функции
Ровно как и в школе, приравняем нулю производную:
Оператор Гамильтона линеен, поэтому мы можем переписать наше уравнение в следующем виде:
Теперь применим вторую и третью теоремы о дифференцировании:
Вспомним, что
Ура-ура, перейдя от одной переменной к многим, мы не потеряли ровным счётом ничего, и можем эффективно минимизировать квадратичные функции!
Переходим к наименьшим квадратам
Наконец мы можем перейти к основному содержанию этой лекции. Представьте, что у нас есть две точки на плоскости
У нас два уравнения с двумя неизвестными (
В общем случае решение существует и единственно. Для удобства перепишем ту же самую систему в матричном виде:
Получим уравнение типа
А теперь представим, что у нас есть три точки, через которые нужно провести прямую:
В матричном виде эта система запишется следующим образом:
Теперь у нас матрица
Нашу систему можно записать в следующем виде:
Или, более кратко,
Векторы
Очевидно, что линейная комбинация
Давайте определим ошибку решения как
Вот иллюстрация:.

Имея заданные векторы
Но постойте, где же наименьшие квадраты? Сейчас будут. Функция извлечения корня
Вполне очевидно, что длина вектора ошибки минимизируется, если он перпендикулярен плоскости, натянутой на векторы
В матричном виде эту же самую систему можно записать как
или же
Но мы на этом не остановимся, так как запись можно ещё больше сократить:
И самая последняя трансформация:
Давайте посчитаем размерности. Матрица
Теорема 4
Это совсем нетрудно показать:
Теорема 5
Это следует из того факта, что
Кроме того,
Итого, для системы с двумя неизвестными мы доказали, что минимизация квадратичной функции
Таким образом, проблема наименьших квадратов
Переходим к практике
Пример первый, одномерный
Давайте вспомним один пример из предыдущей статьи:
# initialize the data array
x = [0.] * 32
x[0] = x[31] = 1.
x[18] = 2.
# smooth the array values other than at indices 0,18,31
for iter in range(1000):
for i in range(len(x)):
if i in [0,18,31]: continue
x[i] = (x[i-1] + x[i+1])/2.
У нас есть обычный массив x из 32 элементов, инициализированный следующим образом:

А затем мы тысячу раз выполним следующую процедуру: для каждой ячейки x[i] мы запишем в неё среднее значение соседних ячеек: x[i] = ( x[i-1] + x[i+1] )/2. Единственное исключение: мы не будем переписывать элементы массива под номерами 0, 18 и 31. Вот так выглядит эволюция массива на первых ста пятидесяти итерациях:

Как мы выяснили в предыдущей статье, оказывается, наш питоновский мегакод на четыре строчки решает следующиую систему линейных уравнений методом Гаусса-Зейделя:

Выяснить-то выяснили, но откуда вообще взялась эта система? Что за магия? Давайте отвлечёмся на секунду, и попробуем решить немного другую систему. У меня по-прежнему есть 32 переменных, но теперь я хочу, чтобы они все-все-все были равны одна другой. Это нетрудно записать, достаточно записать систему уравнений, которая гласит, что все соседние элементы попарно равны:

Вышеприведённый питоновский код в принципе не трогает значения трёх переменных: x0, x18, x31, поэтому давайте их перенесём в правую часть системы уравнений, т.е., исключим из множества неизвестных:

Я фиксирую начальное значение x0=1, первое уравнение говорит, что x1 = x0 = 1, второе уравнение говорит, что x2=x1=x0=1 и так далее, покуда мы не дойдём до уравнения 1 = x0 = x17 = x18 = 2. Ой. А ведь эта система не имеет решения :((
А и пофиг, мы же программисты! Давайте звать на помощь наименьшие квадраты! Наша нерешаемая система может быть записана в матричном виде
Интуитивно можно представлять себе процесс создания матрицы системы следующим образом: мы соединяем пружинками значения, равенства которых хотим добиться. Например, в нашем случае мы хотим, чтобы
Давайте напишем программу, решающую эту систему уравнений. В прошлой статье мы видели, что метод Гаусса-Зейделя очень прост в программировании, но имеет очень медленную сходимость, поэтому лучше бы использовать настоящие решатели систем линейных уравнений. В самом простейшем случае, для нашего одномерного примера, код может выглядеть как-то так:
import numpy as np
n = 32 # size of the vector to produce
# fill the matrix with 2nd order finite differences
A = np.matrix(np.zeros((n-1, n)))
for i in range(0,n-1):
A[i, i] = -1.
A[i, i+1] = 1.
# eliminate the constrained variables from the matrix
A = A[:,[*range(1,18)] + [*range(19,31)]]
b = np.matrix(np.zeros((n-1, 1)))
b[0,0] = 1.
b[17,0] = -2.
b[18,0] = 2.
b[n-2,0] = -1.
# solve the system
x = np.linalg.inv(A.transpose()*A)*A.transpose()*b
x = x.transpose().tolist()[0]
# re-introduce the constrained variables
x.insert(0, 1.)
x.insert(18, 2.)
x.append(1.)
Этот код производит список x из 32 элементов, в котором хранится решение. Мы строим матрицу
Этот код выполняет необходимую работу, но довольно неприятно переносить в правую часть значения фиксированных переменных. Нельзя ли схитрить? Можно! Давайте посмотрим на следующий код:
import numpy as np
n = 32 # size of the vector to produce
# fill the matrix with 2nd order finite differences
A = np.matrix(np.zeros((n-1+3, n)))
for i in range(0,n-1):
A[i, i] = -1.
A[i, i+1] = 1.
# enforce the constraints through the quadratic penalty
A[n-1+0, 0] = 100.
A[n-1+1,18] = 100.
A[n-1+2,31] = 100.
b = np.matrix(np.zeros((n-1+3, 1)))
b[n-1+0,0] = 100.*1.
b[n-1+1,0] = 100.*2.
b[n-1+2,0] = 100.*1.
# solve the system
x = np.linalg.inv(A.transpose()*A)*A.transpose()*b
x = x.transpose().tolist()[0]
С программистской точки зрения он гораздо приятнее, вектор x получается сразу нужной размерности, да и матрицы A и b заполняются куда как проще. Но в чём же хитрость? Давайте запишем систему уравнений, которую мы решаем:

Посмотрите внимательно на последние три уравнения:
100 x0 = 100 * 1
100 x18 = 100 * 2
100 x31 = 100 * 1
Не проще ли было их записать следующим образом?
x0 = 1
x18 = 2
x31 = 1
Нет, не проще. Как я уже говорил, каждое уравнение навешивает пружинки, в данном случае пружинку между x0 и значением 1, пружинку между x18 и значением 2 и, наконец, переменная x31 тоже будет притягиваться к единице.
Но коэффициент 100 там стоит не просто так. Мы же помним, что эта система просто так не решается, мы решаем её в смысле наименьших квадратов, минимизируя соответствующую квадратичную функцию. Умножив на 100 каждый из коэффициентов последних трёх уравнений, мы вводим штраф за отклонение x0, x18 и x32 от нужных значений, в десять тысяч раз (100^2) превышающий штраф за отклонение от равенства
Пример второй, трёхмерный
Давайте уже перейдём к чему-нибудь более интересному, нежели сглаживание элементов одномерного массива! Для начала сделаем ровно то же самое, но на более интересных данных и с настоящим инструментарием. Я хочу взять трёхмерную поверхность, зафиксировать её границу, а всю остальную поверхность максимально сгладить:

Код доступен тут, но на всякий случай приведу полный листинг главного файла:
#include <vector>
#include <iostream>
#include "OpenNL_psm.h"
#include "geometry.h"
#include "model.h"
int main(int argc, char** argv) {
if (argc<2) {
std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl;
return 1;
}
Model m(argv[1]);
for (int d=0; d<3; d++) { // solve for x, y and z separately
nlNewContext();
nlSolverParameteri(NL_NB_VARIABLES, m.nverts());
nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE);
nlBegin(NL_SYSTEM);
nlBegin(NL_MATRIX);
for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices
if (m.opp(i)!=-1) continue;
int v = m.from(i);
nlRowScaling(100.);
nlBegin(NL_ROW);
nlCoefficient(v, 1);
nlRightHandSide(m.point(v)[d]);
nlEnd(NL_ROW);
}
for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior
if (m.opp(i)==-1) continue;
int v1 = m.from(i);
int v2 = m.to(i);
nlRowScaling(1.);
nlBegin(NL_ROW);
nlCoefficient(v1, 1);
nlCoefficient(v2, -1);
nlEnd(NL_ROW);
}
nlEnd(NL_MATRIX);
nlEnd(NL_SYSTEM);
nlSolve();
for (int i=0; i<m.nverts(); i++) {
m.point(i)[d] = nlGetVariable(i);
}
}
std::cout << m;
return 0;
}
Я написал простейший парсер wavefront .obj файлов, поэтому моделька подгружается в одну строчку. В качестве решателя я буду использовать OpenNL, это очень мощный решатель для проблем наименьших квадратов с разреженными матрицами. Обратите внимание, что размеры матриц у нас могут быть гигантскими: например, если мы хотим получить ч/б картинку размером 1000 x 1000 пикселей, то матрица
Итак, давайте смотреть на код. Для начала я объявляю солверу, что я хочу делать:
nlNewContext();
nlSolverParameteri(NL_NB_VARIABLES, m.nverts());
nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE);
nlBegin(NL_SYSTEM);
nlBegin(NL_MATRIX);
Я хочу иметь матрицу
А затем я объявляю строку за строкой нашей матрицы. Для начала я фиксирую вершины, которые находятся на краю поверхности:
for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices
if (m.opp(i)!=-1) continue;
int v = m.from(i);
nlRowScaling(100.);
nlBegin(NL_ROW);
nlCoefficient(v, 1);
nlRightHandSide(m.point(v)[d]);
nlEnd(NL_ROW);
}
Можно видеть, что я использую квадратичный штраф в 100^2 для фиксирования краевых вершин.
Ну а затем для каждой пары смежных вершин я вешаю пружинку жёсткости 1 между ними:
for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior
if (m.opp(i)==-1) continue;
int v1 = m.from(i);
int v2 = m.to(i);
nlRowScaling(1.);
nlBegin(NL_ROW);
nlCoefficient(v1, 1);
nlCoefficient(v2, -1);
nlEnd(NL_ROW);
}
Выполняем код и видим, как лицо сгладилось в поверхность мыльной плёнки на изогнутой проволоке. Мы сейчас только что решили проблему Дирихле, получив поверхность минимальной площади.
Усиляем характеристические черты
Давайте превратим наше лицо в гротескную маску:

В предыдущей статье я уже показывал, как это сделать на коленке, здесь же я привожу настоящий код, использующий солвер наименьших квадратов:
for (int d=0; d<3; d++) { // solve for x, y and z separately
nlNewContext();
nlSolverParameteri(NL_NB_VARIABLES, m.nverts());
nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE);
nlBegin(NL_SYSTEM);
nlBegin(NL_MATRIX);
for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices
if (m.opp(i)!=-1) continue;
int v = m.from(i);
nlRowScaling(100.);
nlBegin(NL_ROW);
nlCoefficient(v, 1);
nlRightHandSide(m.point(v)[d]);
nlEnd(NL_ROW);
}
for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry
if (m.opp(i)==-1) continue;
int v1 = m.from(i);
int v2 = m.to(i);
nlRowScaling(.2);
nlBegin(NL_ROW);
nlCoefficient(v1, 1);
nlCoefficient(v2, -1);
nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]);
nlEnd(NL_ROW);
}
for (int v=0; v<m.nverts(); v++) { // amplify the curvature
nlRowScaling(1.);
nlBegin(NL_ROW);
int nneigh = m.incident_halfedges(v).size();
nlCoefficient(v, nneigh);
Vec3f curvature = m.point(v)*nneigh;
for (int hid : m.incident_halfedges(v)) {
nlCoefficient(m.to(hid), -1);
curvature = curvature - m.point(m.to(hid));
}
nlRightHandSide(2.5*curvature[d]);
nlEnd(NL_ROW);
}
nlEnd(NL_MATRIX);
nlEnd(NL_SYSTEM);
nlSolve();
for (int i=0; i<m.nverts(); i++) {
m.point(i)[d] = nlGetVariable(i);
}
}
Полный код доступен тут. Как он работает? Как и в предыдущем примере, я начинаю с того, что фиксирую краевые вершины. Затем для каждого ребра я (тихонечко, с коэффициентом 0.2) говорю, что неплохо было бы, чтобы оно имело ровно ту же форму, что и в изначальной поверхности:
for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry
if (m.opp(i)==-1) continue;
int v1 = m.from(i);
int v2 = m.to(i);
nlRowScaling(.2);
nlBegin(NL_ROW);
nlCoefficient(v1, 1);
nlCoefficient(v2, -1);
nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]);
nlEnd(NL_ROW);
}
Если больше ничего не делать, и решить проблему прямо как есть, то мы на выходе должны получить ровно то, что было на входе: граница выхода равняется границе входа, плюс перепады на выходе равняются перепадам на входе.
Но мы на этом не останавливемся!
for (int v=0; v<m.nverts(); v++) { // amplify the curvature
nlRowScaling(1.);
nlBegin(NL_ROW);
int nneigh = m.incident_halfedges(v).size();
nlCoefficient(v, nneigh);
Vec3f curvature = m.point(v)*nneigh;
for (int hid : m.incident_halfedges(v)) {
nlCoefficient(m.to(hid), -1);
curvature = curvature - m.point(m.to(hid));
}
nlRightHandSide(2.5*curvature[d]);
nlEnd(NL_ROW);
}
В нашу систему я добавляю ещё уравнений. Для каждой вершины я считаю кривизну поверхности вокруг неё во входной поверхности, и умножаю её на два с половиной, то есть, выходная поверхность должна иметь большую кривизну повсюду.
Затем вызываем наш решатель и получаем неплохую карикатуру.
Последний пример на сегодня
До этого момента мы не видели ни одного нового примера, всё уже было показано в предыдущей статье. Давайте попробуем сделать что-то менее тривиальное, нежели простейшее сглаживание, которое легко можно получить, не используя никаких солверов. Код доступен тут, но давайте я приведу листинг:
#include <vector>
#include <iostream>
#include "OpenNL_psm.h"
#include "geometry.h"
#include "model.h"
const Vec3f axes[] = {Vec3f(1,0,0), Vec3f(-1,0,0), Vec3f(0,1,0), Vec3f(0,-1,0), Vec3f(0,0,1), Vec3f(0,0,-1)};
int snap(Vec3f n) { // returns the coordinate axis closest to the given normal
double nmin = -2.0;
int imin = -1;
for (int i=0; i<6; i++) {
double t = n*axes[i];
if (t>nmin) {
nmin = t;
imin = i;
}
}
return imin;
}
int main(int argc, char** argv) {
if (argc<2) {
std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl;
return 1;
}
Model m(argv[1]);
std::vector<int> nearest_axis(m.nfaces());
for (int i=0; i<m.nfaces(); i++) {
Vec3f v[3];
for (int j=0; j<3; j++) v[j] = m.point(m.vert(i, j));
Vec3f n = cross(v[1]-v[0], v[2]-v[0]).normalize();
nearest_axis[i] = snap(n);
}
for (int d=0; d<3; d++) { // solve for x, y and z separately
nlNewContext();
nlSolverParameteri(NL_NB_VARIABLES, m.nverts());
nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE);
nlBegin(NL_SYSTEM);
nlBegin(NL_MATRIX);
for (int i=0; i<m.nhalfedges(); i++) {
int v1 = m.from(i);
int v2 = m.to(i);
nlRowScaling(1.);
nlBegin(NL_ROW);
nlCoefficient(v1, 1);
nlCoefficient(v2, -1);
nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]);
nlEnd(NL_ROW);
int axis = nearest_axis[i/3]/2;
if (d!=axis) continue;
nlRowScaling(2.);
nlBegin(NL_ROW);
nlCoefficient(v1, 1);
nlCoefficient(v2, -1);
nlEnd(NL_ROW);
}
nlEnd(NL_MATRIX);
nlEnd(NL_SYSTEM);
nlSolve();
for (int i=0; i<m.nverts(); i++) {
m.point(i)[d] = nlGetVariable(i);
}
}
std::cout << m;
return 0;
}
Мы по-прежнему работаем с той же поверхностью, что и раньше; мы вызываем функцию snap() для каждого треугольника. Эта функция говорит, к какой оси системы координат ближе всего нормаль этого треугольника. То есть, мы хотим знать, этот треугольник скорее вертикален или горизонтален. Ну а затем мы хотим изменить геометрию нашей поверхности, чтобы то, что близко к горизонтали, стало ещё ближе! Левая часть вот этой картинки показывает результат работы функции snap():

Итак, мы раскрасили нашу поверхность в три цвета, соответствующие трём осям системы координат. Ну а затем для каждого ребра нашей системы мы добавляем следующие уравнения:
nlRowScaling(1.);
nlBegin(NL_ROW);
nlCoefficient(v1, 1);
nlCoefficient(v2, -1);
nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]);
nlEnd(NL_ROW);
То есть, мы предписываем каждому ребру выходной поверхности походить на соответствующее ребро входной поверхности, жёсткость пружинки 1. А затем, если мы разрешаем, например, размерность x, а ребро должно быть вертикально, то просто говорим, что одна вершина равна другой с жёсткостью пружины 2:
nlRowScaling(2.);
nlBegin(NL_ROW);
nlCoefficient(v1, 1);
nlCoefficient(v2, -1);
nlEnd(NL_ROW);
Ну а вот и результат работы нашей программы:

Вполне резонный вопрос: истуканы с острова Пасхи, это, конечно, круто, но при чём тут геология? Есть ли примеры реальных задач?
Да, конечно. Давайте возьмём один срез земной коры:

Для геологов очень важны слои разных пород, границы (горизонты) между которыми показаны зелёным, и геологические разломы, которые показаны красным. У нас есть на вход сетка треугольников (тетраэдров в 3д) той области, которая нас интересует, но для моделирования определённых процессов необходимы квады (гексаэдры в 3д). Мы деформируем нашу модель так, чтобы разломы стали вертикальными, а горизонты (сюрприз) горизонтальными:

Затем мы просто возьмём регулярную сетку квадратов, нарежем наш домен на равномерные квадратики, и применим к ним обратное преобразование, получив необходимую сетку квадов.
Заключение
Методы наименьших квадратов — мощнейший инструмент обработки данных, и применяется гораздо шире, нежели статистика в колонках экселя. Эти возможности нам открываются благодаря тому, что минимизация квадратичной функции и решение системы линейных уравнений — это одно и то же, а решать линейные уравнения мы (человечество) научились очень и очень хорошо, даже совершенно нечеловеческих размеров с миллиардами переменных.
Однако же бывают случаи, когда линейных моделей нам может не хватить. И тут на помощь могут прийти, например, нейронные сети. В следующей статье я постараюсь показать, что МНК с отбрасыванием выбросов эквивалентен одной из формулировок нейронных сетей. Оставайтесь на линии!