Hello!
[UPD from 12.06.2021: if you're looking for a symbolic algebra library, AngouriMath is actively developed. It's on Github and has a website. Discord for questions]
Why does programming a calculator seem to be a task, which every beginner undertakes? History might have the answer — computers were created for this exact purpose. Unlike the beginners, we will develop a smart calculator, which, although won't reach the complexity of SymPy, will be able to perform such algebraic operations as differentiation, simplification, and equations solving, will have built-in latex support, and have implemented features such as compilation to speed up the computations.
Let's do it!
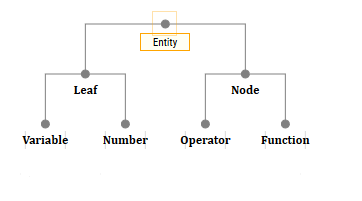
An expression is not a string. It is pretty obvious that a mathematical formula is either a tree or a stack, as it is shown in the example below. Each node of this tree is some kind of an operation, a variable, or a constant.

Each operation is either a function or an operator, which are actually similar to each other. Their children are the arguments of the respective functions/operators.
Of course, the implementation can widely vary. However, the idea is that if your tree only consists of nodes and leaves, then despite their differences from each other, they all are generalized by something. I call these «things» — entities. Therefore, the upper class will be the abstract class Entity.
And there will also be four child classes: NumberEntity, VariableEntity, OperatorEntity, FunctionEntity.
We will start with building an in-code expression, i.e.
If you declare an empty class VariableEntity, then such a code will throw an exception, something like «I don't know how to multiply and add.»
Is a very important and useful feature of most languages, it allows you to customize the execution of arithmetic operations. It is syntactically implemented differently depending on the language. For example, an implementation in C#
Learn more about overriding statements in C#
My implementation is here.
In compilable languages like C#, such a thing is usually present and allows you to cast the type if necessary without an additional call of
Instead of the usual
More on type casting in C#
My implementation here.
The Entity class has a Children field — this is just a list of instances of Entity, which are the arguments for this entity.
When we call a function or operator, we should create a new entity, and put in it the children from which the function or operator is called. For example, the add operator in theory should look something like this:
That is, now if we have entity x and entity 3, then x + 3 will return the entity of the sum operator with two children: 3 and x. So, we can build expression trees.
A function call is simpler and not as beautiful as that with an operator:
My implementation is here.
Ok, we made up an expression tree.
Everything is extremely simple here. We have Entity — we check whether it is a variable itself; if so, we return the value, otherwise we run through the children.
In this «huge» 48-line file implements such a complex function.
Yeah, the calculator must calculate. Here we are supposed to add some kind of method to Entity
The leaf is unchanged, but for everything else we have a custom calculation. Once more, I will only provide an example:
If the argument is a number, then we perform a numerical operation, otherwise we will return the arguments as they were.
This is the simplest unit, number. Arithmetic operations can be performed on it. By default, it is complex. It also has operations such as Sin, Cos, and some others.
If you are interested in its implementation, Number is described here.
Anyone can calculate the derivative numerically, and such a function is written truly in one line:
But of course we want an analytical derivative. Since we already have an expression tree, we can recursively replace each node in accordance with the differentiation rule. It should work something like this:

I realized it in the following way:
Product:
And here is a workaround in itself:
This is the Entity method. As we see, the leaf has only two states: either it is a variable by which we differentiate, then its derivative is 1, or it is a constant (number or VariableEntity), then its derivative is 0, or a node, then there is a reference by name (InvokeDerive refers to the dictionary of functions, where the desired one is located (for example, the sum or sine)).
Notice that I do not leave something like dy/dx here but claim that the derivative of the variable not by which we differentiate is 0. But here it is done differently.
All differentiation is described in a single file.
Simplification of an expression in the general case is non-trivial. Well, for example, which expression is simpler: or
or  ? At this point, we stick to some ideas, and basing on them we want to make those rules so they could accurately simplify the expression.
? At this point, we stick to some ideas, and basing on them we want to make those rules so they could accurately simplify the expression.
It is possible to write at every Eval that if we have the sum node, and its children are product nodes, then we will sort out four options, and if something is equal something else, we will take out the factor… But of course I do not want to do that. Therefore, we will use a system of rules and patterns. So what do we want? Something like this syntax:
Here is an example of a tree in which a subtree was found (circled in green) that matches the pattern any1 + const1 * any1 (any1 found is circled in orange).

As you can see, sometimes it is important for us that one and the same entity must be repeated, for example, to reduce the expression , we need
, we need  to be both factor of the first and second monomial, because
to be both factor of the first and second monomial, because  is no longer reduceable. Therefore, we need to make an algorithm that not only checks that the tree matches the pattern, but also
is no longer reduceable. Therefore, we need to make an algorithm that not only checks that the tree matches the pattern, but also
The entry point looks something like this:
In tree.PaternMakeMatch, we recursively add keys and their values to the dictionary. Here is an example of a list of the Entity pattern itself:
When we write any1 * const1 — func1 and so on, each node will have a number — this is the key. In other words, when filling out the dictionary, these numbers will appear as keys: 100, 101, 200, 201, 400… And when building a tree, we will look at the value corresponding to the key and substitute it.
Implemented here.
In the article, to which I have already referred, the author decided to make it simple, and sorted it practically by the hash of the tree. He managed to reduce and
and  ,
,  to turn
to turn  . But we, of course, also want
. But we, of course, also want  to be reduced, and in general more complicated things.
to be reduced, and in general more complicated things.
In general, patterns, that we used before, are a monstrously wonderful thing. It will allow you to reduce expressions like , and Pythagorean trigonometric identity, and other complex things. But the elementary palm,
, and Pythagorean trigonometric identity, and other complex things. But the elementary palm,  , it will not reduce, because the main rule here is the commutativity of the terms. Therefore, the first step is to extract the «linear children.»
, it will not reduce, because the main rule here is the commutativity of the terms. Therefore, the first step is to extract the «linear children.»
Actually for each node of the sum or difference (and, by the way, the product/division), we want to get a list of terms (factors).

This is basically straightforward. Let the LinearChildren(Entity node) function return a list, then we look at a child in node.Children: if child is not a sum, then result.Add (child), otherwise — result.AddRange (LinearChildren (child)).
Implemented not in the best way here.
So we have a list of children, but what's next? Suppose we have . Obviously, our algorithm will receive five terms. Next, we want to group by similarity, for example,
. Obviously, our algorithm will receive five terms. Next, we want to group by similarity, for example,  looks like
looks like  more than
more than  .
.
Here is a good grouping:

Since the patterns in it will cope further with the conversion of to
to  .
.
That is, we first group by some hash, and then do MultiHang — converting n-ary summation to binary.
On the one hand, and
and  should be placed in one group. On the other hand, in the presence of
should be placed in one group. On the other hand, in the presence of  , placing in the same group with
, placing in the same group with  is pointless.
is pointless.
Therefore, we implement multi-level sorting. First, we pretend that and
and  to be the same. Then we pretend that
to be the same. Then we pretend that  can be placed only with other
can be placed only with other  ,
,  etc. Finally,
etc. Finally,  is only compatible with
is only compatible with  . And now our
. And now our  and
and  finally merged. Implemented quite simply:
finally merged. Implemented quite simply:
As you can see, the function entity affects sorting in any way (of course, because with
with  is cannot be somehow reduced). Likewise, we cannot reduce
is cannot be somehow reduced). Likewise, we cannot reduce  with
with  . But the constants and operators are taken into account at some levels (but not all). That is how it is performed
. But the constants and operators are taken into account at some levels (but not all). That is how it is performed
I sort the tree here.
In quotation marks — since it is not in the IL code itself, but only in a very fast set of instructions. But it is very simple.
To calculate the value of a function, we just need to call the variable substitution and eval, for example
But it works slowly, about 1.5 microseconds per sine.
To speed up the calculation, we do a function calculation on the stack, namely:
1) We come up with the FastExpression class, which will have a list of instructions
2) When compiling, the instructions are stacked in the reverse order, that is, if there is a function , then the instructions will be something like this:
, then the instructions will be something like this:
Next, when invoked, we run these instructions and return a Number.
An example of executing a sum statement:
The sine call time was reduced from 1500ns to 60ns (system Complex.Sin takes 30ns).
It is implemented here.
There is still «room for improvement.» Let some function be
According to benchmarks, its performance (time/iteration) (i7-7700hq) is the following:
As we can see, this function has repeating parts, for example, , and it would be nice to cache them.
, and it would be nice to cache them.
To do this, we introduce two more instructions PULLCACHE and TOCACHE. The first one will push onto the stack the number in the cache at the address that we pass to it. The second will copy (
It remains to make a table into which during compilation we will write functions for caching. What we will not cache? Well, firstly, what happens once. The extra instruction to access the cache is not good. Secondly, operations that are too simple also make no sense to cache, such as accessing a variable or number.
When interpreting the list of instructions, we will have a pre-created array for caching. Now the instructions for this function look like
Finally, we get a clearly better result:
Compilation and interpretation of instructed are located here.
This is a well-known format for mathematical formulas (although not only them!), which is rendered into a more human-readable format. It is also used on Habr, and all the formulas that I write are just written in this format.
Having an expression tree makes rendering in latex very simple. How to do this in terms of logic? So, we have the top of the tree. If it is a number or a variable, then everything is simple. If this vertex, for example, is a division operator, we want instead of
instead of  (
( and
and  are the children of the vertex), so for division we write something like
are the children of the vertex), so for division we write something like
Everything is very simple, as we see. The only problem I encountered during the implementation is that it is not clear how to place braces. If we just wrap each operator with braces, we will get such nonsense:
In contrast, if you completely remove them, then given an expression of the form , we will print
, we will print
It is resolved simply, we enter the priorities of the operators like
Latexisation is here. By the way, word «latexise» does not exist, I invented it myself.
Actually, from the point of view of mathematics, you cannot write an algorithm that finds all the solutions of some equation. Therefore, we want to find as many different roots as possible, realizing the unattainability of the final goal. There are two components: a numerical solution (everything is as simple as possible) and analytical (that is the thing).
It is extremely simple, given the function we will search for the root using the iterative formula
we will search for the root using the iterative formula
Since roots might be also located in a complex plane, we can basically write a two-dimensional loop that will look for solutions and then return unique ones. In this case, we can now find the derivative of the function analytically, and then compile both functions and
and  .
.
Newton's method is located here.
First thoughts are pretty obvious. Clearly, the roots of equation are equal to the set of roots
are equal to the set of roots  and
and  , similarly for division:
, similarly for division:
For sine, this will be realized a little different:
After all, we want to find all the roots, and not just those that are 0.
After we have made sure that the current expression is not a product, and not other easily simplified operators and functions, we need to try to find a template for solving the equation.
The first idea is to use the patterns we made to simplify the expression. And in fact, we will need approximately this, but first we need to do a variable replacement. And indeed, to the equation
there is no pattern, but to the pair
there is a pattern of a quadratic expression and arcsin.
Therefore, we are to develop a function «GetMinimumSubtree», which would return the most efficient variable replacement. What is an effective replacement? This is such a replacement in which we
After replacing the equation looks a lot simpler.
So, the first thing we do is , turning it into
, turning it into  . Now, after the disclosure, we get something like
. Now, after the disclosure, we get something like
Not canonical? Then we first collect information about each monomial by applying “linear children” and expanding all the terms.
What do we have about the monomial? A monomial is a product of factors, one of which is a variable, or an operator of the degree of a variable and an integer. Therefore, we will introduce two variables, one will have a degree, and the other a coefficient. Next, we simply go through the factors, and each time we are convinced that either is there to an integer degree, or without a degree at all. If we encounter something unexpected — we return with null.
is there to an integer degree, or without a degree at all. If we encounter something unexpected — we return with null.
Okay, we have compiled a dictionary in which the key is a degree (of a polynomial) (integer) and the value is a monomial coefficient. This is what it looks like for the previous example:
That is how solving of the quadratic equation is implemented
This thing has not yet been completed, but in general this is here.
So, here we have made some kind of replacement like , and now we want to find
, and now we want to find  from there. Here we just have a step-by-step deployment of functions and operators, such as
from there. Here we just have a step-by-step deployment of functions and operators, such as
The code snippet looks something like this:
The code for these functions is here.
Everything, the final solving algorithm of the equations (yet!) Looks something like this
That's it for now. Because this article is the translation of the two in Russian (first and second parts), it only contains features realized up to the moment of 9-th January. However, we implemented tons of new features and have something to tell. Soon, there will be the third part.
There are also a couple of examples of how the project works:

Thanks for your attention!
[UPD from 12.06.2021: if you're looking for a symbolic algebra library, AngouriMath is actively developed. It's on Github and has a website. Discord for questions]
Why does programming a calculator seem to be a task, which every beginner undertakes? History might have the answer — computers were created for this exact purpose. Unlike the beginners, we will develop a smart calculator, which, although won't reach the complexity of SymPy, will be able to perform such algebraic operations as differentiation, simplification, and equations solving, will have built-in latex support, and have implemented features such as compilation to speed up the computations.
What are the articles about?
It will superficially tell about assembling an expression, parsing from a string, variable substitution, analytic derivative, equation numerical solving, and definite integration, rendering to LaTeX format, complex numbers, compiling functions, simplifying, expanding brackets, and blah blah blah.
For those who urgently need to clone something, repository link.
For those who urgently need to clone something, repository link.
Let's do it!
Whom is this article for?
I think that the article may be useful for a beginner, but maybe those who are a little more experienced will also find something interesting. However, I hope to write an article so that it can be read without being a C# programmer at all.
To those who have already seen it
Expression assembly
When I was a child...
...I wanted to write a calculator. What did it have to do? The four basic operations, that was enough. My goal was to calculate the value from a string expression, for example, «1 + (3/4 — (5 + 3 * 1))». I started my favorite Delphi 7 and wrote a parser, which first recursively processed parentheses, and then replaced the expression in parentheses with the calculated value, and removed the braces. Basically, a quite working way for me at that time.
What is an expression?
An expression is not a string. It is pretty obvious that a mathematical formula is either a tree or a stack, as it is shown in the example below. Each node of this tree is some kind of an operation, a variable, or a constant.

Each operation is either a function or an operator, which are actually similar to each other. Their children are the arguments of the respective functions/operators.
Class hierarchy in your code
Of course, the implementation can widely vary. However, the idea is that if your tree only consists of nodes and leaves, then despite their differences from each other, they all are generalized by something. I call these «things» — entities. Therefore, the upper class will be the abstract class Entity.
Abstract?
As everyone knows from basic programming courses, an abstract class generalizes some classes on the one hand, and allows you to separate the logic and behavior of some objects on the other. An instance of an abstract class cannot be created, but its child can.
And there will also be four child classes: NumberEntity, VariableEntity, OperatorEntity, FunctionEntity.
How to build an expression?
We will start with building an in-code expression, i.e.
var x = new VariableEntity("x");
var expr = x * x + 3 * x + 12;
If you declare an empty class VariableEntity, then such a code will throw an exception, something like «I don't know how to multiply and add.»
Overriding Operators
Is a very important and useful feature of most languages, it allows you to customize the execution of arithmetic operations. It is syntactically implemented differently depending on the language. For example, an implementation in C#
public static YourClass operator +(YourClass a, YourClass b) {
return new YourClass(a.ToString() + b.ToString());
}
Learn more about overriding statements in C#
My implementation is here.
(Ex|Im)plicit type casting
In compilable languages like C#, such a thing is usually present and allows you to cast the type if necessary without an additional call of
myvar.ToAnotherType(). So, for example, it would be more convenient to writeNumberEntity myvar = 3;
Instead of the usual
NumberEntity myvar = new NumberEntity(3);
More on type casting in C#
My implementation here.
Hanging
The Entity class has a Children field — this is just a list of instances of Entity, which are the arguments for this entity.
Thoughts
In fact, only two classes of the four can have children: OperatorEntity and FunctionEntity. We could have created, say, NodeEntity, inherited these two classes from it, created a LeafEntity, and inherit VariableEntity and NumberEntity from it.

When we call a function or operator, we should create a new entity, and put in it the children from which the function or operator is called. For example, the add operator in theory should look something like this:
public static Entity operator +(Entity a, Entity b){
var res = new OperatorEntity("+");
res.Children.Add(a);
res.Children.Add(b);
return res;
}
That is, now if we have entity x and entity 3, then x + 3 will return the entity of the sum operator with two children: 3 and x. So, we can build expression trees.
A function call is simpler and not as beautiful as that with an operator:
public Entity Sin(Entity a)
{
var res = new FunctionEntity("sin");
res.Children.Add(a);
return res;
}
My implementation is here.
Ok, we made up an expression tree.
Variable substitution
Everything is extremely simple here. We have Entity — we check whether it is a variable itself; if so, we return the value, otherwise we run through the children.
In this «huge» 48-line file implements such a complex function.
Value calculation
Yeah, the calculator must calculate. Here we are supposed to add some kind of method to Entity
public Entity Eval()
{
if (IsLeaf)
{
return this;
}
else
return MathFunctions.InvokeEval(Name, Children);
}
The leaf is unchanged, but for everything else we have a custom calculation. Once more, I will only provide an example:
public static Entity Eval(List<Entity> args)
{
MathFunctions.AssertArgs(args.Count, 1);
var r = args[0].Eval();
if (r is NumberEntity)
return new NumberEntity(Number.Sin((r as NumberEntity).Value));
else
return r.Sin();
}
If the argument is a number, then we perform a numerical operation, otherwise we will return the arguments as they were.
Number?
This is the simplest unit, number. Arithmetic operations can be performed on it. By default, it is complex. It also has operations such as Sin, Cos, and some others.
If you are interested in its implementation, Number is described here.
Derivative
Anyone can calculate the derivative numerically, and such a function is written truly in one line:
public double Derivative(Func<double, double> f, double x) => (f(x + 1.0e-5) - f(x)) * 1.0e+5;
But of course we want an analytical derivative. Since we already have an expression tree, we can recursively replace each node in accordance with the differentiation rule. It should work something like this:

I realized it in the following way:
public static Entity Derive(List<Entity> args, VariableEntity variable) {
MathFunctions.AssertArgs(args.Count, 2);
var a = args[0];
var b = args[1];
return a.Derive(variable) + b.Derive(variable);
}
Product:
public static Entity Derive(List<Entity> args, VariableEntity variable)
{
MathFunctions.AssertArgs(args.Count, 2);
var a = args[0];
var b = args[1];
return a.Derive(variable) * b + b.Derive(variable) * a;
}
And here is a workaround in itself:
public Entity Derive(VariableEntity x)
{
if (IsLeaf)
{
if (this is VariableEntity && this.Name == x.Name)
return new NumberEntity(1);
else
return new NumberEntity(0);
}
else
return MathFunctions.InvokeDerive(Name, Children, x);
}
This is the Entity method. As we see, the leaf has only two states: either it is a variable by which we differentiate, then its derivative is 1, or it is a constant (number or VariableEntity), then its derivative is 0, or a node, then there is a reference by name (InvokeDerive refers to the dictionary of functions, where the desired one is located (for example, the sum or sine)).
Notice that I do not leave something like dy/dx here but claim that the derivative of the variable not by which we differentiate is 0. But here it is done differently.
All differentiation is described in a single file.
Simplification of an expression. Patterns
Simplification of an expression in the general case is non-trivial. Well, for example, which expression is simpler:
It is possible to write at every Eval that if we have the sum node, and its children are product nodes, then we will sort out four options, and if something is equal something else, we will take out the factor… But of course I do not want to do that. Therefore, we will use a system of rules and patterns. So what do we want? Something like this syntax:
{ any1 / (any2 / any3) -> any1 * any3 / any2 },
{ const1 * var1 + const2 * var1 -> (const1 + const2) * var1 },
{ any1 + any1 * any2 -> any1 * (Num(1) + any2) },
Here is an example of a tree in which a subtree was found (circled in green) that matches the pattern any1 + const1 * any1 (any1 found is circled in orange).

As you can see, sometimes it is important for us that one and the same entity must be repeated, for example, to reduce the expression
- Verify that the same Entity patterns match the same Entity.
- Gathers list of entites matching each pattern entity
The entry point looks something like this:
internal Dictionary<int, Entity> EqFits(Entity tree)
{
var res = new Dictionary<int, Entity>();
if (!tree.PatternMakeMatch(this, res))
return null;
else
return res;
}
In tree.PaternMakeMatch, we recursively add keys and their values to the dictionary. Here is an example of a list of the Entity pattern itself:
static readonly Pattern any1 = new Pattern(100, PatType.COMMON);
static readonly Pattern any2 = new Pattern(101, PatType.COMMON);
static readonly Pattern const1 = new Pattern(200, PatType.NUMBER);
static readonly Pattern const2 = new Pattern(201, PatType.NUMBER);
static readonly Pattern func1 = new Pattern(400, PatType.FUNCTION);
When we write any1 * const1 — func1 and so on, each node will have a number — this is the key. In other words, when filling out the dictionary, these numbers will appear as keys: 100, 101, 200, 201, 400… And when building a tree, we will look at the value corresponding to the key and substitute it.
Implemented here.
Simplification. Tree Sort
In the article, to which I have already referred, the author decided to make it simple, and sorted it practically by the hash of the tree. He managed to reduce
Will the patterns not work for that?
In general, patterns, that we used before, are a monstrously wonderful thing. It will allow you to reduce expressions like
Linear children
Actually for each node of the sum or difference (and, by the way, the product/division), we want to get a list of terms (factors).

This is basically straightforward. Let the LinearChildren(Entity node) function return a list, then we look at a child in node.Children: if child is not a sum, then result.Add (child), otherwise — result.AddRange (LinearChildren (child)).
Implemented not in the best way here.
Grouping children
So we have a list of children, but what's next? Suppose we have
Here is a good grouping:

Since the patterns in it will cope further with the conversion of
That is, we first group by some hash, and then do MultiHang — converting n-ary summation to binary.
Node Hash
On the one hand,
Thoughts
If you think about it, then  . Although it seems to me, this is practically not easier, and certainly not necessary. Anyway, simplification is never an obvious thing, and this is certainly not the first thing to write when writing a “calculator”.
. Although it seems to me, this is practically not easier, and certainly not necessary. Anyway, simplification is never an obvious thing, and this is certainly not the first thing to write when writing a “calculator”.
Therefore, we implement multi-level sorting. First, we pretend that
internal string Hash(SortLevel level)
{
if (this is FunctionEntity)
return this.Name + "_" + string.Join("_", from child in Children select child.Hash(level));
else if (this is NumberEntity)
return level == SortLevel.HIGH_LEVEL ? "" : this.Name + " ";
else if (this is VariableEntity)
return "v_" + Name;
else
return (level == SortLevel.LOW_LEVEL ? this.Name + "_" : "") + string.Join("_", from child in Children where child.Hash(level) != "" select child.Hash(level));
}
As you can see, the function entity affects sorting in any way (of course, because
public Entity Simplify(int level)
{
// First, we make the easiest simplification: calculating values where possible, multiplying by zero, etc.
var stage1 = this.InnerSimplify();
Entity res = stage1;
for (int i = 0; i < level; i++)
{
// This block is responsible for sorting. First we group something like x and x + 1 (variables and functions), then something like x-1 and x + 1 (variables, functions and constants), then something like x + 1 and x + 1 (everything is taken into account).
switch (i)
{
case 0: res = res.Sort(SortLevel.HIGH_LEVEL); break;
case 2: res = res.Sort(SortLevel.MIDDLE_LEVEL); break;
case 4: res = res.Sort(SortLevel.LOW_LEVEL); break;
}
// Here we replace the patterns.
res = TreeAnalyzer.Replace(Patterns.CommonRules, res).InnerSimplify();
}
return res;
}
Thoughts
Is this the best implementation? I have been thinking for a long time how to make it maximally beautiful, although in my opinion, it is far from «beautiful» here.
I sort the tree here.
«Compilation» of functions
In quotation marks — since it is not in the IL code itself, but only in a very fast set of instructions. But it is very simple.
Substitution Problem
To calculate the value of a function, we just need to call the variable substitution and eval, for example
var x = MathS.Var("x");
var expr = x * x + 3;
var result = expr.Substitute(x, 5).Eval();
But it works slowly, about 1.5 microseconds per sine.
Instructions
To speed up the calculation, we do a function calculation on the stack, namely:
1) We come up with the FastExpression class, which will have a list of instructions
2) When compiling, the instructions are stacked in the reverse order, that is, if there is a function
PUSHVAR 0 // Variable Substitution Number 0 - x
CALL 6 // Call function №6 - sine
PUSHCONST 3
CALL 0 // Call function №0 - sum
PUSHVAR 0
PUSHVAR 0
CALL 2
CALL 0
Next, when invoked, we run these instructions and return a Number.
An example of executing a sum statement:
internal static void Sumf(Stack<Number> stack)
{
Number n1 = stack.Pop();
Number n2 = stack.Pop();
stack.Push(n1 + n2);
}
The sine call time was reduced from 1500ns to 60ns (system Complex.Sin takes 30ns).
It is implemented here.
Cache
There is still «room for improvement.» Let some function be
According to benchmarks, its performance (time/iteration) (i7-7700hq) is the following:
| Method | Time (nanoseconds) |
|---|---|
| Substitute | 6800 |
| Our compiled function | 650 |
| The same function written directly in code | 430 |
What?
Substitute — the classic way of calculating the value of an expression, i.e. for example
Our compiled function is when we do the same, but after compiling it
A function written directly in code is when we do
var x = MathS.Var("x");
var expr = x + 3 * x;
Console.WriteLine(expr.Substitute(x, 5).Eval());
>>> 20
Our compiled function is when we do the same, but after compiling it
var x = MathS.Var("x");
var expr = x + 3 * x;
var func = expr.Compile(x);
Console.WriteLine(func.Substitute(5));
A function written directly in code is when we do
static Complex MyFunc(Complex x)
=> x + 3 * x;
As we can see, this function has repeating parts, for example,
To do this, we introduce two more instructions PULLCACHE and TOCACHE. The first one will push onto the stack the number in the cache at the address that we pass to it. The second will copy (
stack.Peek()) the last number from the stack to the cache, also at a specific address.It remains to make a table into which during compilation we will write functions for caching. What we will not cache? Well, firstly, what happens once. The extra instruction to access the cache is not good. Secondly, operations that are too simple also make no sense to cache, such as accessing a variable or number.
When interpreting the list of instructions, we will have a pre-created array for caching. Now the instructions for this function look like
PUSHCONST (2, 0)
PUSHVAR 0
CALL powf
TOCACHE 0 #at this point we compute n^2, and since we need it more than once, we cache it.
CALL sinf
TOCACHE 1 #we will also need sin(n^2)
PULLCACHE 0 #when we encounter mention of a cached function, we pull the apporpriate element.
PULLCACHE 0
CALL cosf
PULLCACHE 1
CALL sumf
CALL sumf
CALL sumf
Finally, we get a clearly better result:
| Method | Time (nanoseconds) |
|---|---|
| Substitute | 6800 |
| Our compiled functions | 330 (previous result: 650) |
| The same function written directly in code | 430 |
Compilation and interpretation of instructed are located here.
LaTeX
This is a well-known format for mathematical formulas (although not only them!), which is rendered into a more human-readable format. It is also used on Habr, and all the formulas that I write are just written in this format.
Having an expression tree makes rendering in latex very simple. How to do this in terms of logic? So, we have the top of the tree. If it is a number or a variable, then everything is simple. If this vertex, for example, is a division operator, we want
public static class Div
{
internal static string Latex(List<Entity> args)
=> @"\frac{" + args[0].Latexise() + "}{" + args[1].Latexise() + "}";
}
Everything is very simple, as we see. The only problem I encountered during the implementation is that it is not clear how to place braces. If we just wrap each operator with braces, we will get such nonsense:
In contrast, if you completely remove them, then given an expression of the form
It is resolved simply, we enter the priorities of the operators like
args[0].Latexise(args[0].Priority < Const.PRIOR_MUL) + "*" + args[1].Latexise(args[1].Priority < Const.PRIOR_MUL);
Latexisation is here. By the way, word «latexise» does not exist, I invented it myself.
Solving Equations
Actually, from the point of view of mathematics, you cannot write an algorithm that finds all the solutions of some equation. Therefore, we want to find as many different roots as possible, realizing the unattainability of the final goal. There are two components: a numerical solution (everything is as simple as possible) and analytical (that is the thing).
Numerical solution. Newton's Method
It is extremely simple, given the function
Since roots might be also located in a complex plane, we can basically write a two-dimensional loop that will look for solutions and then return unique ones. In this case, we can now find the derivative of the function analytically, and then compile both functions
Newton's method is located here.
Analytical Solution
First thoughts are pretty obvious. Clearly, the roots of equation
internal static void Solve(Entity expr, VariableEntity x, EntitySet dst)
{
if (expr is OperatorEntity)
{
switch (expr.Name)
{
case "mul":
Solve(expr.Children[0], x, dst);
Solve(expr.Children[1], x, dst);
return;
case "div":
Solve(expr.Children[0], x, dst);
return;
}
}
...
For sine, this will be realized a little different:
case "sinf":
Solve(expr.Children[0] + "n" * MathS.pi, x, dst);
return;
After all, we want to find all the roots, and not just those that are 0.
After we have made sure that the current expression is not a product, and not other easily simplified operators and functions, we need to try to find a template for solving the equation.
The first idea is to use the patterns we made to simplify the expression. And in fact, we will need approximately this, but first we need to do a variable replacement. And indeed, to the equation
there is no pattern, but to the pair
there is a pattern of a quadratic expression and arcsin.
Therefore, we are to develop a function «GetMinimumSubtree», which would return the most efficient variable replacement. What is an effective replacement? This is such a replacement in which we
- Maximize the use of this replacement
- Maximize the depth of the tree (so that in the equation
we have the replacement
)
- We make sure that with this substitution we replaced all the mentions of the variable, for example, if in the equation
we make the replacement
, then we will not be able to solve it. Therefore, in this equation, the best replacement for
is
(that is, there is no good replacement), but for example in
we can safely do the replacement
.
After replacing the equation looks a lot simpler.
Polynomial
So, the first thing we do is
expr.Expand() — open all the brackets to get rid of the muck of the form Not canonical? Then we first collect information about each monomial by applying “linear children” and expanding all the terms.
What do we have about the monomial? A monomial is a product of factors, one of which is a variable, or an operator of the degree of a variable and an integer. Therefore, we will introduce two variables, one will have a degree, and the other a coefficient. Next, we simply go through the factors, and each time we are convinced that either
Feh
If we suddenly come across some  ,
,  and other things that mention
and other things that mention  , but do not fit the monomial pattern is bad.
, but do not fit the monomial pattern is bad.
Okay, we have compiled a dictionary in which the key is a degree (of a polynomial) (integer) and the value is a monomial coefficient. This is what it looks like for the previous example:
0 => c
1 => 1
2 => 3
3 => 1 - a
That is how solving of the quadratic equation is implemented
if (powers[powers.Count - 1] == 2)
{
var a = GetMonomialByPower(2);
var b = GetMonomialByPower(1);
var c = GetMonomialByPower(0);
var D = MathS.Sqr(b) - 4 * a * c;
res.Add((-b - MathS.Sqrt(D)) / (2 * a));
res.Add((-b + MathS.Sqrt(D)) / (2 * a));
return res;
}
This thing has not yet been completed, but in general this is here.
Reverse replacement
So, here we have made some kind of replacement like
The code snippet looks something like this:
switch (func.Name)
{
case "sinf":
// sin(x) = value => x = arcsin(value)
return FindInvertExpression(a, MathS.Arcsin(value), x);
case "cosf":
// cos(x) = value => x = arccos(value)
return FindInvertExpression(a, MathS.Arccos(value), x);
case "tanf":
// tan(x) = value => x = arctan(value)
return FindInvertExpression(a, MathS.Arctan(value), x);
...
The code for these functions is here.
Everything, the final solving algorithm of the equations (yet!) Looks something like this
- If we know the zero of the function or operator, send Solve there (for example, if
, then run Solve(a) and Solve(b))
- Find a replacement
- Solve as a polynomial, if possible
- For all solutions, deploy a replacement to get the final solution
- If, as a polynomial, it did not resolve and we have only one variable, we solve it by Newton’s method
That's it for now. Because this article is the translation of the two in Russian (first and second parts), it only contains features realized up to the moment of 9-th January. However, we implemented tons of new features and have something to tell. Soon, there will be the third part.
There are also a couple of examples of how the project works:
var x = MathS.Var("x");
var y = MathS.Var("y");
var c = x * y + x / y;
Console.WriteLine(MathS.Sqr(c));
>>> (x * y + x / y) ^ 2
var x = MathS.Var("x");
var expr = x * 2 + MathS.Sin(x) / MathS.Sin(MathS.Pow(2, x));
var subs = expr.Substitute(x, 0.3);
Console.WriteLine(subs.Eval());
>>> 0,9134260185941638
var x = MathS.Var("x");
var func = MathS.Sqr(x) + MathS.Ln(MathS.Cos(x) + 3) + 4 * x;
var derivative = func.Derive(x);
Console.WriteLine(derivative.Eval());
>>> 2 * x + -1 * sin(x) / (cos(x) + 3) + 4
var x = MathS.Var("x");
var a = MathS.Var("a");
var b = MathS.Var("b");
var expr = MathS.Sqrt(x) / x + a * b + b * a + (b - x) * (x + b) +
MathS.Arcsin(x + a) + MathS.Arccos(a + x);
Console.WriteLine(expr.Simplify());
>>> 1.5707963267948966 + 2 * a * b + b ^ 2 + x ^ (-0.5) - x ^ 2
var x = MathS.Var("x");
var y = MathS.Var("y");
var expr = x.Pow(y) + MathS.Sqrt(x + y / 4) * (6 / x);
Console.WriteLine(expr.Latexise());
>>> {x}^{y}+\sqrt{x+\frac{y}{4}}*\frac{6}{x}
var x = MathS.Var("x");
var expr = MathS.Sin(x) + MathS.Sqrt(x) / (MathS.Sqrt(x) + MathS.Cos(x)) + MathS.Pow(x, 3);
var func = expr.Compile(x);
Console.WriteLine(func.Substitute(3));
>>> 29.4752368584034
Entity expr = "(sin(x)2 - sin(x) + a)(b - x)((-3) * x + 2 + 3 * x ^ 2 + (x + (-3)) * x ^ 3)";
foreach (var root in expr.Solve("x"))
Console.WriteLine(root);
>>> arcsin((1 - sqrt(1 + (-4) * a)) / 2)
>>> arcsin((1 + sqrt(1 + (-4) * a)) / 2)
>>> b
>>> 1
>>> 2
>>> i
>>> -i
Thanks for your attention!