В связи с все более широким распространением доступных лазерных сканеров (лидаров), способных получать 3D облака точек (3dОТ) и все более широким применением этой технологии в различных областях (от машиностроения до безопасности, от нефтяной промышленности до архитектуры), оживился интерес к алгоритмам обработки облаков точек.
Одно из востребованных применений 3dОТ в промышленности — это создание конструкторской документации на только возводимое, старое или переделанное оборудование, которое обычно представляет из себя трубопроводы и другие конструкции цилиндрической геометрии.
Для детектирования геометрических примитивов в 3dОТ обычно применяются специализированные 3D библиотеки, например Microsoft PCL. У подхода с использованием готовых библиотек наряду с достоинствами есть и недостатки. Например, трудно включить их в уже существующие кадовские схемы обработки, которые обычно имеют 2D размерность.
Рассмотрим, как можно было бы обрабатывать 3dОТ, например насосной станции, начав с 2D сечений и используя весь арсенал 2D обработки, который есть в надежных и оптимизированных библиотеках обработки изображений, например OpenCV.

Рисунок 1. 3D ОТ модель насосной станции
Основным элементом сечений, полученных при сканировании различных трубных конструкций являются эллиптические дуги.

Рисунок 2. Горизонтальное сечение 3D модели насосной станции на среднем уровне
Для данной статьи, ограничим нашу задачу рассмотрением одного ключевого алгоритма, позволяющего детектировать произвольные эллиптические дуги — это итеративный алгоритм роста дуговых сегментов и связывания краев (region growth and edge linking).
Ростовые алгоритмы являются наиболее наглядными и легко верифицируемыми, хотя и трудоемкими по сравнению со статистическими алгоритмами, которые лучше подходят для случая, когда сцена содержит слабо связанные, отдаленные объекты, которые принадлежат одному эллипсу. Эти алгоритмы будут рассмотрены в следующих статьях.
Нахождение метрики контуров
Пока, для простоты, опустим процедуру получения сечения из исходного файла 3dОТ, препроцессинг сечения, его кластеризацию для изолирования геометрических примитивов, а так же последующую привязку, ректификацию и другие фотограмметрические операции, нужные для получения параметров модели. Не станем так же обсуждать параметризацию эвристических поисковых алгоритмов. Опишем все основные операции, из которых строится алгоритм.
Будем считать, что нам необходимо детектировать (распознать, классифицировать) эллиптическую дугу(то есть вычислить параметры эллипса, а так же начальный и конечный угол эллиптической дуги) на данном снимке, вырезанном из горизонтального сечения облака точек.

Рисунок 3. Одна из эллиптических дуг сечения 3D модели (после сглаживания)
Для того чтобы минимизировать работу с растром вслепую, все операции с растром будем проводить через оконтуривание.
OpenCV процедура findContours находит на растре mat, все внешние (без внутренних фигур) контура contours в виде вектора векторов целочисленных точек (в координатах растра):
Mat mat(size);
vector<vector<Point>> contours;
findContours(mat, contours, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE);Это наша ключевая операция, которая в некоторых простых случаях полностью решает поставленную задачу. Но так как не всегда встречаются вырожденные случаи, рассмотрим подробнее технологию обработки через оконтуривание.
Обратная операция, генерация растра по имеющемуся внешнему контуру с помощью OpenCV функции, так же выглядит просто:
drawContours(mat, contours, -1, Scalar(255), -1);
Она тоже очень часто используется для маскирования контура, рисования или для вычисления площади.
Таким образом, на начальном этапе мы имеем набор патчей (кусочков некоторой кривой), который нужно связать в эллиптическую дугу, отбраковав попавшие в сечение части других компонентов конструкции (например, крепежных элементов) или оптический шум, возникающий из-за затенения при сканировании и других причин.
Создадим дискриминантную функцию, которая будет возвращать тип контура (эллипс, линейный отрезок, штриховка или что то еще), а так же концевые точки контура и его повернутый габаритный прямоугольник:
contourTypeSearch(
const vector<Point> &contour, Vec4i &def, RotatedRect &rc);
Соотношения длины и ширины прямоугольника помогает быстро дискриминировать контура, близкие линейным отрезкам, а так же небольшие шумовые контура.
Повернутый прямоугольник в OpenCV имеет непростую систему координат. Если требуется не сам угол, а его тригонометрические функции, все более менее очевидно из контекста. Если же используется абсолютное значение угла, надо учесть, что угол отсчитывается от горизонтали до первого ребра прямоугольника против часовой и имеет отрицательное значение.
Концевые точки эллиптических контуров находятся с помощью нашей процедуры, которая получает на вход растр mat с дискриминируемым контуром, выделенным из исходного изображения маскированием и возвращает максимальный дефект:
contourConvFeature(mat, &def, … );Основным кодом этой функции является вызов двух процедур OpenCV:
vector<int> *hull = new vector<int>();
convexHull(contour, *hull);
vector<Vec4i> *defs = new vector<Vec4i>();
convexityDefects(contour, *hull, *defs);Первая процедура находит выпуклый многоугольник для исследуемого контура, вторая – вычисляет все дефекты выпуклости.
Мы берем только самый большой по значению выпуклости дефект, считая что он и определяет концевые точки контура. Это может быть не так, если внешняя или внутренняя границы контура имеют особенности. Для того чтобы их сгладить, мы применяем дополнительное сглаживание к исследуемому контуру (а не ко всему изображению, чтобы не «замылить» перешейки между контурами, и не нарушить исходную топологию).

Рисунок 4. Вычисление дефекта выпуклости
Вариант(а) ошибочно определяет красную концевую точку. Вариант(б) правильно определяет концевые точки. Вариант(в) переопределяет концевые точки на исходной фигуре.
Так как в принятой нами технологии контур каждый раз регенерируется, приходится заново искать точки соответствия (вернее их индексы) процедурой полного перебора:
nearestContourPtIdx(const vector<Point> &contour, const Point& pt);Для случаев, когда от особенностей не удается полностью избавиться, был так же реализован дополнительный режим разделения дуг(работа отдельно с внутренней/внешней дугой). Это важно например в тех случаях, когда внешняя дуга контура соприкасается с другими объектами или зашумлена. В таком случае, можно перейти на работу с внутренней дугой. В рассматриваемом случае обрабатывать отдельно внешнюю и внутреннюю дуги не нужно.
Так же, по известной формуле о соотношении выпуклости дуги приблизительно оценивается радиус окружности и слишком большие эллипсы отбраковываются:
R = bulge / 2 + SQR(hypot) / (8 * bulge);Таким образом, для всех контуров найдена их метрика дефекта выпуклости (или они классифицированы как линейные или малые и выведены из процедуры). На последнем этапе, к исходной метрике добавляются дополнительные параметры, такие как параметр повернутого габарита и др. и полный набор исследуемых метрик упорядочивается размеру.
typedef tuple<int , //индекс контура
RotatedRect, //его повернутый прямоугольник
Vec4i, //его дефект выпуклости
int> //тип контура
RectDefMetric;Алгоритм связывания сегментов дуг по конечным точкам
Ростовой алгоритм является наглядным и очевидным: берем самый большой контур в качестве затравки и пытаемся ее растить, то есть найти и присоединить к ее концевым точкам ближайшие патчи, удовлетворяющие условиям роста. В выращенную фигуру вписываем искомую эллиптическую дугу. Маскируем и вычитаем фигуру из исходного набора. Повторяем ростовую процедуру пока исходное множество не иссякнет.
Основная процедура ростового алгоритма выглядит так:
vector<Point> *patch =
growingContours(contour, def, tmp, hull);где contour — исследуемый контур, def — его дефект выпуклости, hull — выпуклый многоугольник всего региона, tmp — вспомогательная буферная матрица. На выходе получаем векторный выращенный контур.
Процедура состоит из цикла попыток роста затравки, заканчивающихся либо исчерпанием доступных патчей для роста, либо ограничена параметром максимального числа итераций.

Рисунок 5. Множество патчей для роста без затравки
Главная сложность — выбрать ближайшие патчи к концевым точкам контура, такие чтобы фигура росла только вперед. За тангенциальное направление примем усредненную прямую, принадлежащую дуге, в окрестности концевой точки. На Рисунке 6 показаны кандидаты для присоединения к затравке на некоторой итерации.

Рисунок 6. Затравка, окруженная множеством ростовых патчей-кандидатов
Для каждого патча-кандидата вычисляется следующая метрика:
typedef tuple<
double, //расстояние от одной из 2х точек роста до одного из 2х концов патча
bool, bool, //флаги, определяющие 4 перестановочные комбинации
int, //индекс патча
Vec4i> //его дефект выпуклости
DistMetric;Учитываются только патчи, попавшие в тангенциальный конус. Затем выбирается патч с наименьшим расстоянием и, путем впечатывания в растр соединительного отрезка, соединяется с соответствующим концом затравки. Для другого конца затравки производится поиск подходящего по параметрам патча, и если найден, тоже соединяется с затравкой. Затем затравка маскируется и вычитается из множества патчей. Процедура повторяется с самого начала.
По окончании ростовой процедуры, мы получили эллиптическую дугу, которую предстоит верифицировать.
Для начала, используя стандартну OpenCV процедуру, которая получает наш патч (в виде контура, мы помним, что контур и растр у нас взаимозаменяемы) и возвращает повернутый габарит, то есть полный эллипс.
RotatedRect box = fitEllipse(patch);Затем, забракуем слишком большие и слишком маленькие эллипсы, а потом применим нашу оригинальную процедуру сравнения площадей полученной эллиптической дуги и исходного ростового патча в растровом виде. Эта процедура включает в себя некоторые трюки с маскировкой, поэтому ее описание пока опустим.
И наконец, найдем оставшиеся параметры детектированного эллипса — начальный и конечный угол (полуоси мы уже знаем из fitEllipse).
Для определения начального и конечного угла поступим следующим образом: преобразуем наш полный эллипс, обратно в полигон и прямым перебором найдем его ближайшие к нашим концам точки. Их угловые координаты(фактически, индексы) и будут начальным и конечным углами эллиптической дуги. В коде это выглядит так (немного упростив):
pair<int, int>
ellipseAngles(const RotatedRect &box,
vector<Point> &ell, const Point &ps,
const Point &pe, const Point &pm)
{
vector<Point> ell0;
ellipse2Poly(Point(box.center.x, box.center.y),
Size(box.size.width / 2, box.size.height / 2),
box.angle, 0, 355, 5, ell0);
int i0 = nearestContourPtIdx(ell0, ps);
int i1 = nearestContourPtIdx(ell0, pe);
cutSides(ell0, i0, i1, i2, ell, nullptr);
return pair<int, int>(i0, i1);
}Наша процедура cutSides учитывает топологию обхода эллиптической дуги. Всего надо рассмотреть восемь возможных случаев обхода индексов i0, i1, i2. Идем ли мы по внешнему контуру или по внутреннему и какой из индексов больше, начальный или конечный?
Легче посмотреть код:
void cutSides(
const vector<Point> &ell0, int i0, int i1, int i2,
vector<Point> *ell_in, vector<Point> *ell_out)
{
if (i0 < i1) {
if (i2 > i0 && i2 < i1) {
if (ell_in) {...}
if (ell_out) {...}
} else {
if (ell_in) {...}
if (ell_out) {...}
}}
else {
if (i2 > i1 && i2 < i0) {
if (ell_in) {...}
if (ell_out) {...}
} else {
if (ell_in) {...}
if (ell_out) {...}
}}}Некоторые результаты детектирования эллипсов в сложных случаях, показаны на Рисунке 7.
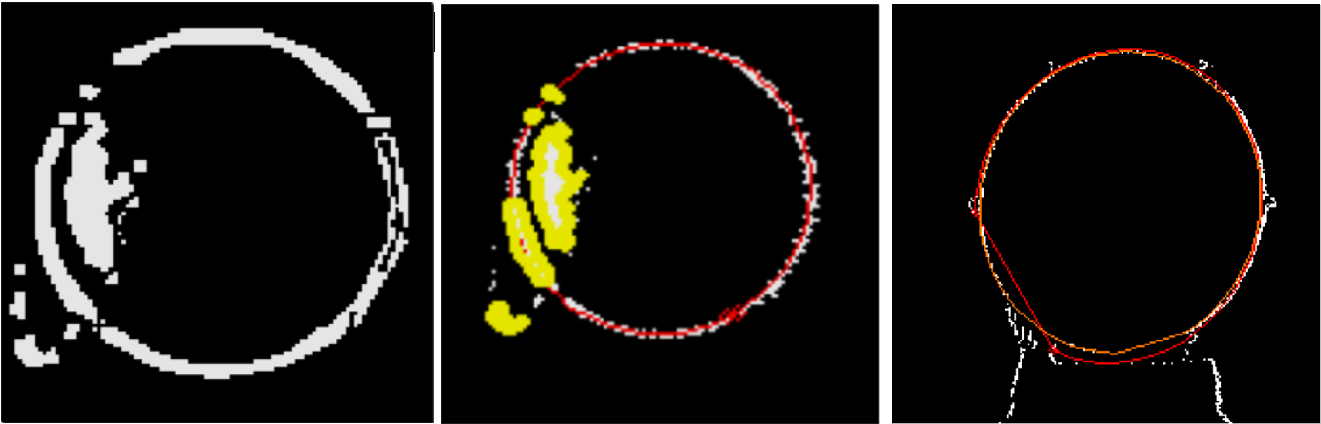
В следующих статьях рассмотрим статистические методы детектирования.