
Введение
Паттерны всегда меня очаровывали. Даже не важно какие. Я экспериментировал со многими: сети, листья и их переплетения, ветви, молнии, флокирование, очертания фигур, реки, скальный осадок, пейзажи, слизистая плесень, лишайники, взаимодействие и расплавление, клеточные автоматы, некоторые фракталы и другие штуки. Мне кажется, что самое приятное — это то, как сложные и затейливые результаты можно получить от набора простых правил.

В последнее время мне были особенно интересны биологические образы и дифференциальный рост. У меня есть опыт в вычислительной математике, но не в биологии. Поэтому у меня мало знаний в том, как биологические системы работают. И всё же, я экспериментировал довольно много над воссозданием различных биологических закономерностей. Одна из сложностей заключается в том, чтобы попытаться воссоздать некоторые образы или закономерности максимально малым количеством простых правил.
Иногда мне удается воссоздать явление, которое я собирался создать, а иногда — нет. Чаще всего я получаю нечто интересное, даже если это не всегда то, что было задумано.
Признание
Буду честным перед вами, я иногда беру идею для своей работы из работ других художников. Особенно Джареда Тарбелла и Nervous System. К примеру, алгоритм, который я назвал Орбиталь (изображение ниже) сделан с очень сильной опорой на Happy Place Тарбелла.

Я указываю на это, потому что мне всегда было сложно понять, где программа, и в моем конкретном случае — изображения, генерируемые этой программой, достаточно уникальны, чтобы рассматриваться, как отдельная работа.
Inconvergent (несосредоточенный)
Я начал работать с генеративными алгоритмами, когда должен был готовиться к экзаменам в университете. Именно поэтому я купил домен inconvergent.net, насмехаясь над тем, как я уклоняюсь от учёбы. Первое, что я сделал — скопировал несколько алгоритмов Тарбелла с помощью Javascript/Canvas. Через некоторое время ко мне начали приходить уже собственные идеи.

Первым моим работающим алгоритмом, помимо Orbitals, был Hyphae. Он получился, когда я пытался воссоздать поведение гифы, сделанное Nervous System. На тот момент я не понимал, насколько сложный этот алгоритм на самом деле, и я потратил очень много времени, тщетно пытаясь сделать что-то сносное. Я все же смог сделать его, а еще вы можете прочитать работу Зигграфа (ENG) по этой теме, если интересно. Увлекательное чтиво!
Код
Я выкладываю почти весь свой код на Github. Все следующие разделы имеют ссылку на соответствующий репозиторий. К сожалению, не все из них хорошо документированы или обновлены.
HYPHAE (ГИФА) [GITHUB]
Я начал экспериментировать с системой, где я выращивал связанные друг с другом круги, которые не могли накладываться друг на друга. Работает это так: вы где-нибудь помещаете начальный (круг), и задаёте ему радиус и направление движения. Затем пытаетесь добавить новый узел по периметру первого узла в направлении движения. Важно иметь направление движения, чтобы было немного «колебания», и каждый раз угол немного отклонялся. Также обязательно каждый раз при добавление нового делаете радиус новых узлов немного меньше предыдущего.
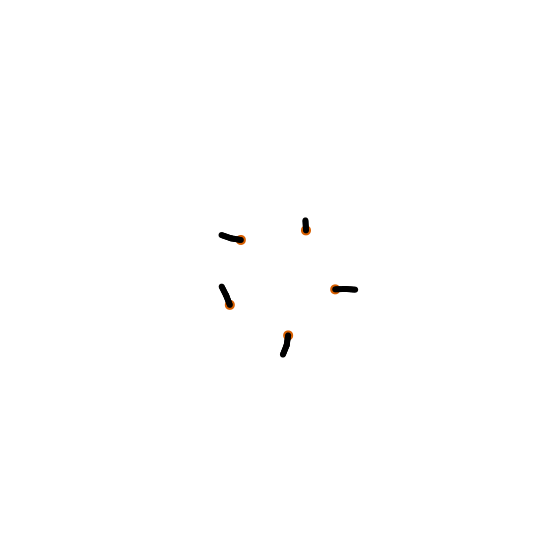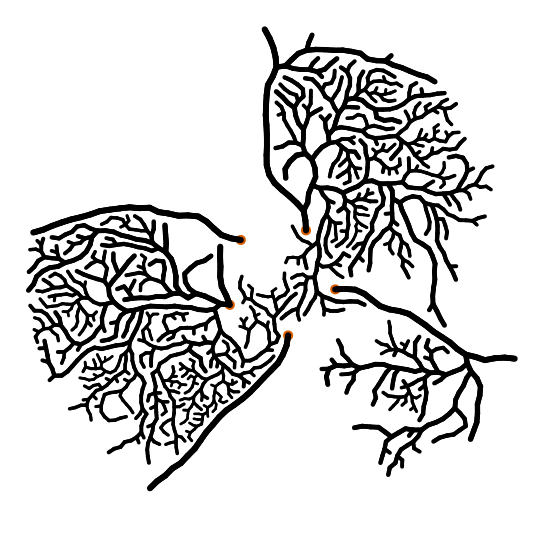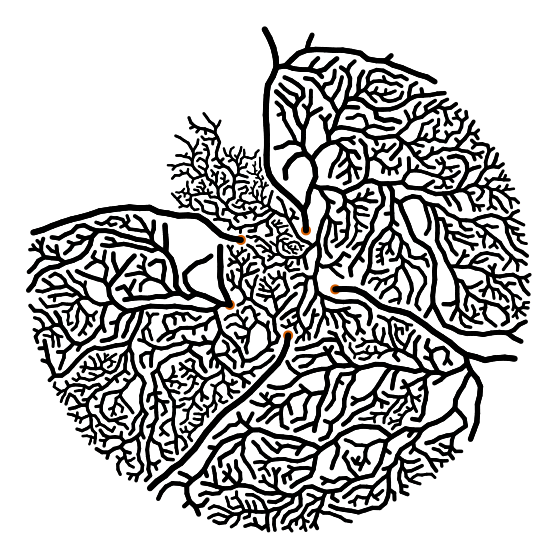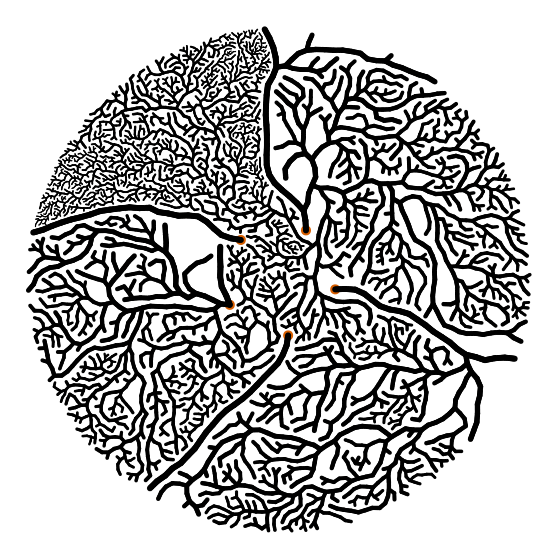
Чтобы получить ветви, можно выбрать узлы наугад и попытаться вырастить новый узел более-менее перпендикулярно направлению движения ветви. И либо узлы столкнутся, либо вы получите новую ветку. Для более интересных результатов можно сделать углы отклонений пропорциональными ширине (радиусу) ветки. Более толстые ветки, как правило, прямее, чем тонкие. И вы, очевидно, можете сделать ещё много других вещей. Например, вы получите радикально разные результаты, если настроите то, сколько «гибких» ветвей вырастет по мере их утончения.
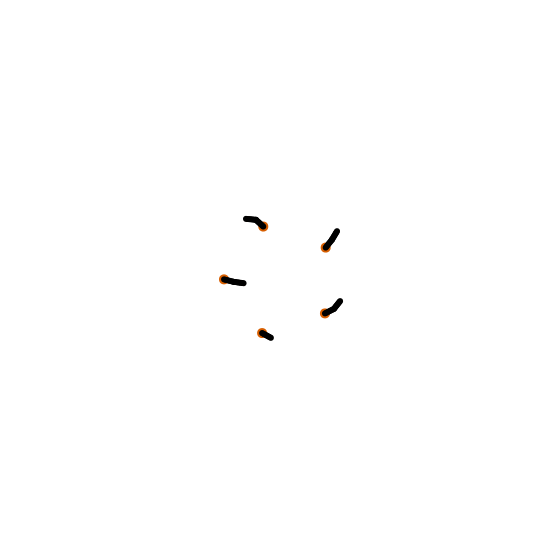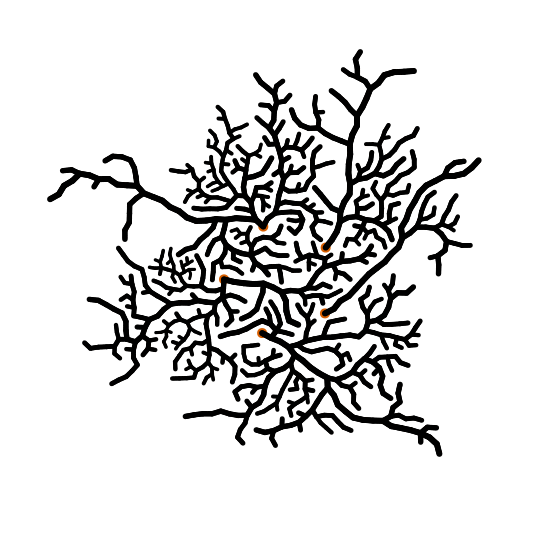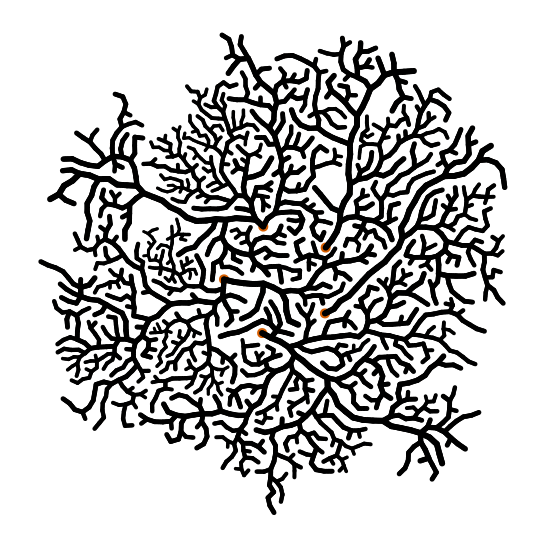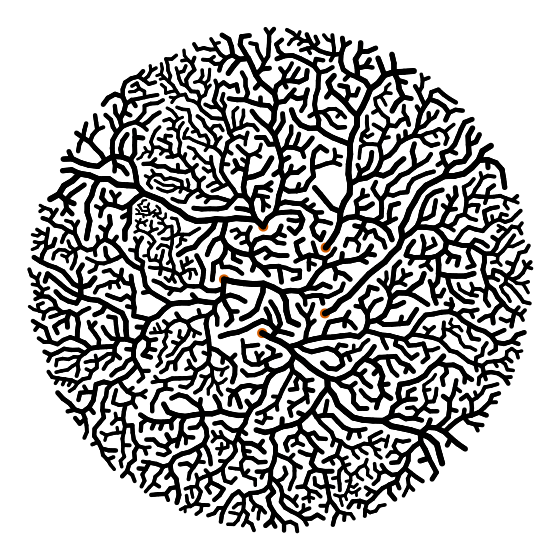
И ещё одно небольшое примечание: когда ветка откололась от существующей ветви, нужно сделать для нее радиус значительно тоньше ветви-предшественника. Вы можете увидеть это на деревьях в реальной жизни. Суть в том, что масса должна быть примерно одинаковой до и после пересечения ветки. (Я где-то вычитал это, но я не могу найти где).
Деревья [GITHUB]
Когда мы говорили о ветках, я понял, что можно упомянуть и маленький эксперимент с деревьями, ведь они похожи по сути.

Я хотел попробовать вырастить ветви таким же образом, как в Гифе, но только так, чтобы новые ветви появлялись только на «концах» других ветвей. К тому же, я не хотел обращать внимания на столкновения или что-нибудь подобное в этой симуляции. Получились не совсем деревья, но результат выглядит вполне реалистично, если не всматриваться сильно.
Наверное, самое интересное то, что нет ни одного реального дерева, выросшего из ствола фиксированной ширины, в отличие от этих «деревьев». Деревья растут как в высоту, так и в ширину с течением времени, и это очень динамичный процесс с множеством факторов. Получается, этот алгоритм имеет очень мало общего с реальными деревьями, но несколько несложных правил этого алгоритма по-прежнему позволяют получить достойный результат, имитируя реальные деревья.

Чтобы придать деревьям эффект глубины, я добавляю тень к ветвям по мере их роста. Эта иллюзия далее развивается, добавляя все больше теней с одной стороны.
Повторяющиеся линии [GITHUB]
В отличие от Гифы, на которую меня вдохновила биология, и от алгоритмов деревьев, следующий пример основан на картинах, нарисованных рукой Джона Френзена. По большому счёту, Френзен рисует линии, где каждая линия следует по контуру ранее нарисованной линии. Каждая последующая линия будет немножко изменяться, и вскоре появляются интересные узоры.
Рисовать фигуры на компьютере довольно легко. Линия состоит из ряда вершин (точек) с ребром (сегментом) между ними. Для создания треугольника вам нужно взять три ребра и соединить их тремя вершинами. Чтобы нарисовать круг, нужно сделать то же самое, только нужно достаточно много вершин, чтобы было «невозможно» увидеть, что это на самомо деле не круг. Если у вас появились сомнения в подходе, то сразу скажу, что есть более сложные и точные способы рисования форм, но этот достаточно прост и точен.
Это значит, что рисовать эти линии так же, как Френсен, можно путём рисования округлых фигур со множеством вершин. Отслеживание формы немного сложнее, но есть несколько способов, которые можно опробовать. Я хотел, чтобы поведение имитировало то, как в реальности рисуется фигура, мало-помалу, при этом продолжая предыдущие линии. Алгоритм, который я придумал работал не совсем так. То есть, он не избегал столкновений, но результаты все равно выглядели очень хорошо.

Чтобы проследить контур, можно выбрать некоторые из соседних рёбер в предыдущей линии, рассчитать среднее направление этих рёбер и добавить вершину к текущей линии вдоль этого направления. Затем добавить несколько случайных движений для имитации рисунка от руки. Некоторое время такой подход работает довольно хорошо, но есть некоторая «инертность», которую можно увидеть в результатах, форма адаптируется слишком медленно.
Количество шума, которое вы добавляете к каждой вершине, имеет решающее значение. Этот шум является тем, что заставляет всю систему создавать интересные формы, ибо коррекция формы вынуждает в процессе пытаться повторить как общее движение, так и некоторые случайные искажения.
Далее идет несколько более сложная система, которая тоже включает в себя линии.
Дифференциальная линия [GITHUB]
Дифференциал — это тот алгоритм, который я давно хотел сделать. В какой-то момент решение просто само возникло у меня в голове, и мне удалось заставить алгоритм работать. Я хотел создать систему, которая вела бы себя так же, как поверхности в природе, которые разворачиваются друг из друга. Например, как грецкие орехи или слои капусты, (не буду даже рассказывать, сколько времени я провел времени за гуглением изображений красной капусты, разрезанной пополам), наш кишечник и некотороые виды листьев и цветочных лепестков. И, вероятно, многие другие вещи.
Прежде чем я начал прикидывать способы, я видел только Floraform, созданный Nervous System, но вам стоит увидеть ещё Cellular Forms Энди Ломаса. Другой важный документ, который я обнаружил гораздо позже, находится здесь.
Сначала я попытался использовать метод, основанный на фрактальной кривой Коха. Но со случайным ростом, а не симметричным и регулярным, как во фрактале. Я так и не доделал и быстро сдался. Однако, через некоторое время (плюс-минус шесть месяцев), я понял, что мог бы ввести новые узлы, пока кривая Коха «растёт», но нужно заставить эти узлы смещаться относительно друг друга. Таким образом, они могли бы корректировать их позиции динамически, как жемчуг на верёвочке. Так они смогут держать нужное расстояние от других узлов (жемчужин).
Алгоритм выглядит следующим образом. Сначала мы создаем набор узлов, соединённых в какую-нибудь форму (круги или линии подойдут). Затем мы случайным образом вводим новые узлы между парами существующих узлов. В каждой итерации узлы будут пытаться оптимизировать свои позиции. Они будут «хотеть» быть рядом, но не слишком близко к своим двум соседям. В то же время они будут хотеть быть как можно дальше от всех других узлов. Обратите внимание, что здесь нет возможности их столкновения.

Есть ряд факторов, которые могут повлиять на поведение этой системы. Один из них — то, как часто мы вводим новые узлы. Другой — максимальное расстояние, в пределах которого узлы будут избегать друг друга. И самое интересное (на мой взгляд) — то, как мы выбираем, куда вставлять новые узлы. Мы можем сделать это равномерно, как в гифке выше, или мы можем расставить приоритетные места, где изгибы кривой будут более острыми, как в гифке ниже.

Разницу не очень легко заметить на данных примерах, но она становится очень заметной на больших симуляциях. На рисунке ниже использован метод вставки на основе кривизны, а создание заняло около 40 часов.

Еще один способ добиться интересных результатов от этого алгоритма — это покрасить кривую специально под каждый шаг во времени. Визуальные и текстурные результаты заметно отличаются, но легко распознать одни и те же характеристики системы.


А если генеративное искусство и визуализация данных, вас заинтересовали — посмотрите другие посты degenerative_art, вот самые популярные на данный момент: