https://www.youtube.com/playlist?list=PLwr8DnSlIMg0KABru36pg4CvbfkhBofAi
Как-то на Хабре мне попалась довольно любопытная статья “Научно-технические мифы, часть 1. Почему летают самолёты?”. Статья довольно подробно описывает, какие проблемы возникают при попытке объяснить подъёмную силу крыльев через закон Бернулли или модель подъёмной силы Ньютона (Newtonian lift). И хотя статья предлагает другие объяснения, мне бы всё же хотелось остановиться на модели Ньютона подробнее. Да, модель Ньютона не полна и имеет допущения, но она даёт более точное и интуитивное описание явлений, чем закон Бернулли.
Основной недостаток этой модели — это отсутствие взаимодействия частиц газа друг с другом. Из-за этого при нормальных условиях она даёт некорректные результаты, хотя всё ещё может применяться для экстремальных условий, где взаимодействием можно пренебречь.
Я же решил проверить, что же произойдёт в модели Ньютона если её улучшить. Что если добавить в неё недостающий элемент межатомного взаимодействия? Исходный код и бинарники получившегося симулятора доступны на GitHub.
Перед тем как мы начнём, я бы хотел сразу обозначить, что это статься не о физике самой модели. Эта статья о GPGPU-программировании. Мы не будем рассматривать физические свойства самой модели, потому что она груба и не подходит для настоящих расчётов. И всё же, эта неточная модель даёт куда более интуитивное описание явления подъёмной силы, чем закон Бернулли.
Computational Fluid Dynamics
Вообще, задачами точной симуляции поведений жидкостей и газов занимается вычислительная гидродинамика (Computational fluid dynamics, CFD), где жидкости и газы в общем случае хорошо описываются уравнениями Навье-Стокса.
Если вас пугает внешний вид этих уравнений, но вы хотели бы разобраться, то для вас есть очень хорошее объяснение в 7-м томе лекций Ричарда Фейнмана/The Feynman Lectures on Physics, Volume II. Загляните в главы 38 (“Упругость”), 40 (“Течение ‘сухой’ воды”) и 41 (“Течение ‘мокрой’ воды”). Ну или просто посмотрите это видео.
Если совсем кратко и на пальцах, то система уравнений Навье-Стокса — это векторное уравнение второго закона Ньютона. Эта система определяет равнодействующую всех сил (давления, вязкости и гравитации) для всех направлений. Как правило, дополнительно задают второе векторное уравнение, обеспечивающее условие несжимаемости.
Принципиально систему уравнений можно решать двумя подходами: методами Эйлера или Лагранжа. Эйлеров подход рассматривает среду как поля векторных и скалярных величин. Подход Лагранжа рассматривает отдельно каждую частицу среды.
Один из многих способов численно решить систему уравнений — это применить метод конечных элементов в связке с адаптивным сеточным методом в случае подхода Эйлера. Зачем нужна адаптивность сетки и как её можно реализовать, подробно и доступно рассказали ребята из SpaceX в своём докладе. Эйлеров подход как правило, но не обязательно, применяется для моделирования замкнутых объемов неразрывных сред, т. е. тех, в которых отсутствуют пустые места и включения других сред. Для иных сред чаще всего реализуют подход Лагранжа, через метод сглаженных частиц (Smoothed-particle hydrodynamics, SPH) или finite point method. Оба метода активно применяются для моделирования воды с полным набором явлений: брызги, капли, лужи, смачивание поверхностей и т. д. Можно даже сымитировать пену или пузыри, если включить в модель частицы воздуха. Реконструкцию поверхности, а точнее изоповерхности, можно произвести любым интересующим вас способом (screen-space meshes, dual contouring, marching tetrahedra, metaballs). Если вы знаете другие интересные подходы, добро пожаловать в комментарии.
UPD: пользователи в комментариях также упоминули о существовании метода конечных объёмов (Finite Volume Method). Мне удалось найти сравнение метода конечных элементов с методом конечных объёмов.
Discrete Element Method
Моей задачей было найти такой подход, который позволит обсчитывать миллионы частиц и наблюдать за эволюцией системы практически в реальном времени.
Метод дискретного элемента (Discrete Element Method, DEM) показался мне очень привлекательным, потому что он решает практически схожую задачу. Однако он в первую очередь предназначен для сыпучих и гранулированных сред, где у каждой частицы в трёхмерном пространстве есть позиция, ориентация, произвольная форма и масса.
Чтобы упростить вычисления, я решил оставить у частиц только две степени свободы (координаты X и Y), одинаковую массу и радиус. При построении своей модели в угоду производительности я хотел отбросить параметры и факторы, которые порождают эффекты второго порядка. Однако при моделировании сложных систем они могут быть очень существенны. Один из показательных примеров — это использование NASA модели идеального газа вместо реального при проектировании космических челноков. В результате, во время миссии STS-1 проявились различные аномалии при входе в атмосферу. Подробнее в разделе Mission Anomalies.
У DEM есть одна важная особенность — это обнаружение столкновений постфактум (Discrete Collision Detection). Разрешение столкновений происходит простым силовым воздействием по закону Гука.
В противоположность этому подходу существует априорный метод Continuous Collision Detection (CCD), который рассчитывает, когда столкновение произойдёт в будущем. Зная точное время контакта, можно скорректировать временной шаг, и избежать неприятных физических артефактов. Метод активно применяется в современных играх. Для игр CCD очень важен чтобы объекты не туннелировали друг через друга, не проваливались друг в друга и не «застревали в текстурах». Метод поддерживается современными движками, в Unity и в Unreal точно.
Подробный доклад о методе Continuous Collision Detection
Но у CCD есть две большие проблемы. Первая — это при всей своей точности он непропорционально ресурсоёмок. А для большого количества частиц он сделает расчёты совершенно непрактичными. Вторая — при увеличении плотности частиц, время свободного пробега каждой уменьшается, вынуждая симулятор делать всё меньшие и меньшие шаги, чтобы не пропустить столкновения. В одном из моих проектов очень хорошо видно, как временной шаг вырождается практически в ноль по мере увеличения плотности “планетарных сгустков”
Поэтому, из практических соображений я решил воспользоваться апостериорной методикой обнаружения столкновений из DEM.
Эффект пушечного ядра
Разработав первую версию симуляции, я обнаружил, что частицы, сталкивающиеся с фронтальной частью крыла, ведут себя очень знакомо. Передняя кромка крыла за счёт своей каплевидной формы при столкновении с набегающим потоком воздуха ударяется об него, расталкивая молекулы. Отраженные частицы создают ударную волну, которая отражает следующие. А те в свою очередь воздействуют на следующий слой и так далее.
Я слышал о подобном эффекте в одном документальном фильме от National Geographic. В нём рассказывалось, что это явление напрямую эксплуатировалось конструкторами космического челнока. Они сознательно сделали нос челнока тупым, чтобы на высоких скоростях он создавал ударную волну, которая защищает выдающиеся части фюзеляжа от разрушительной плазмы.

Ударная волна создаёт щит (изображение National Geographic)
В фильме этот эффект сравнили с пушечным ядром. Летать далеко — не задача ядер. Их задача — ударять. Им не нужна аэродинамическая форма. Именно поэтому тупой нос челнока так хорошо защищает весь аппарат.
Подробнее по ссылке с таймкодом https://youtu.be/cx8XbaQNnxw?t=2206
Удивительно, но именно этот эффект отлично наблюдается в симуляции. Вероятно, именно это взаимодействие слоёв воздуха в сочетании с углом атаки даёт ту самую подъёмную силу. На тепловой карте (heatmap) давления ниже отчётливо видны области высокого (красный и оранжевый цвета) и низкого (зелёный и синий) давления. Наличие взаимодействия между частицами сделало модель Ньютона интереснее.
Картинки ниже кликабельны и доступны в высоком разрешении.
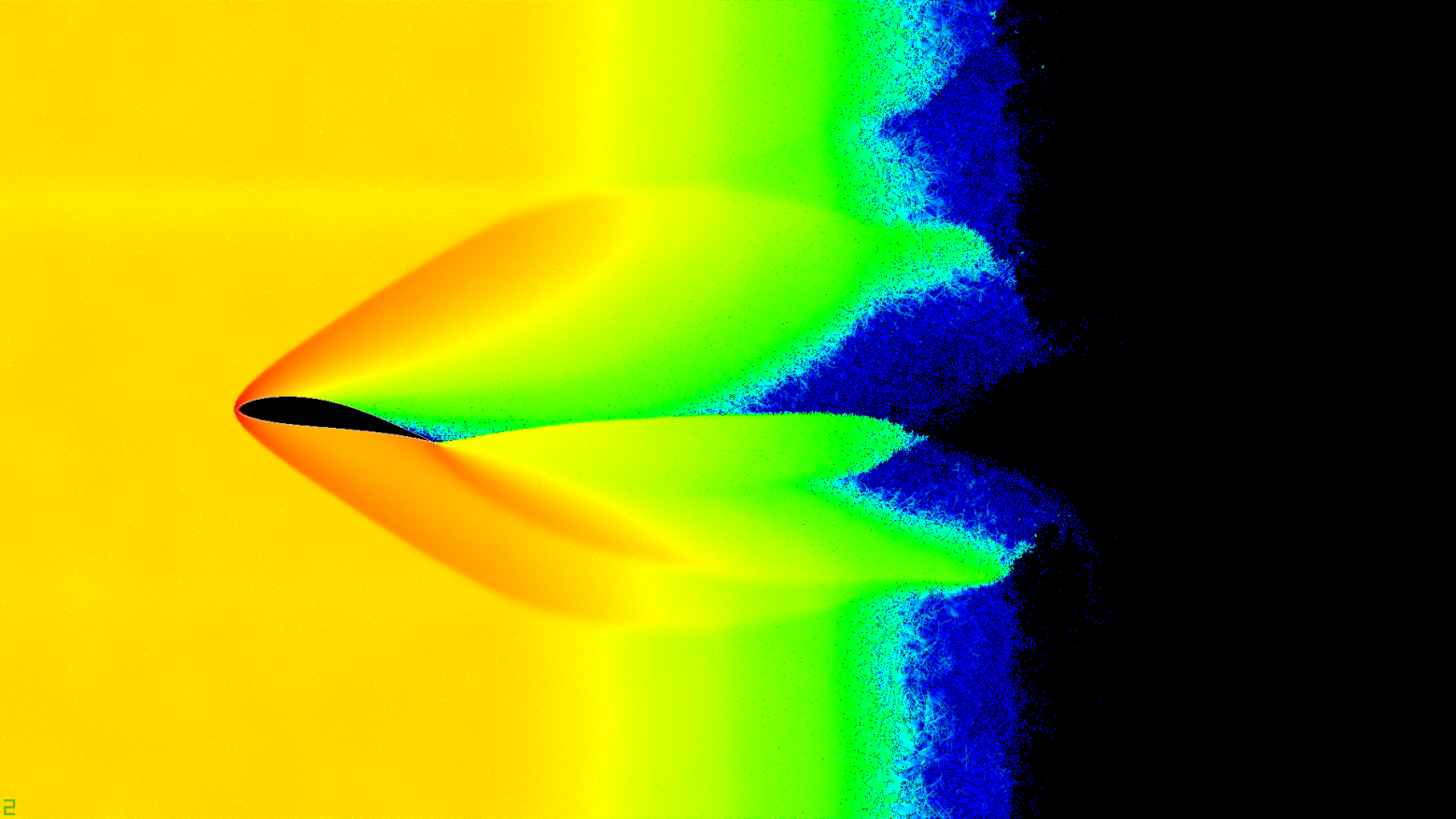
Тепловая карта давления (скалярная сумма модулей сил)

Та же карта, только при большем масштабе
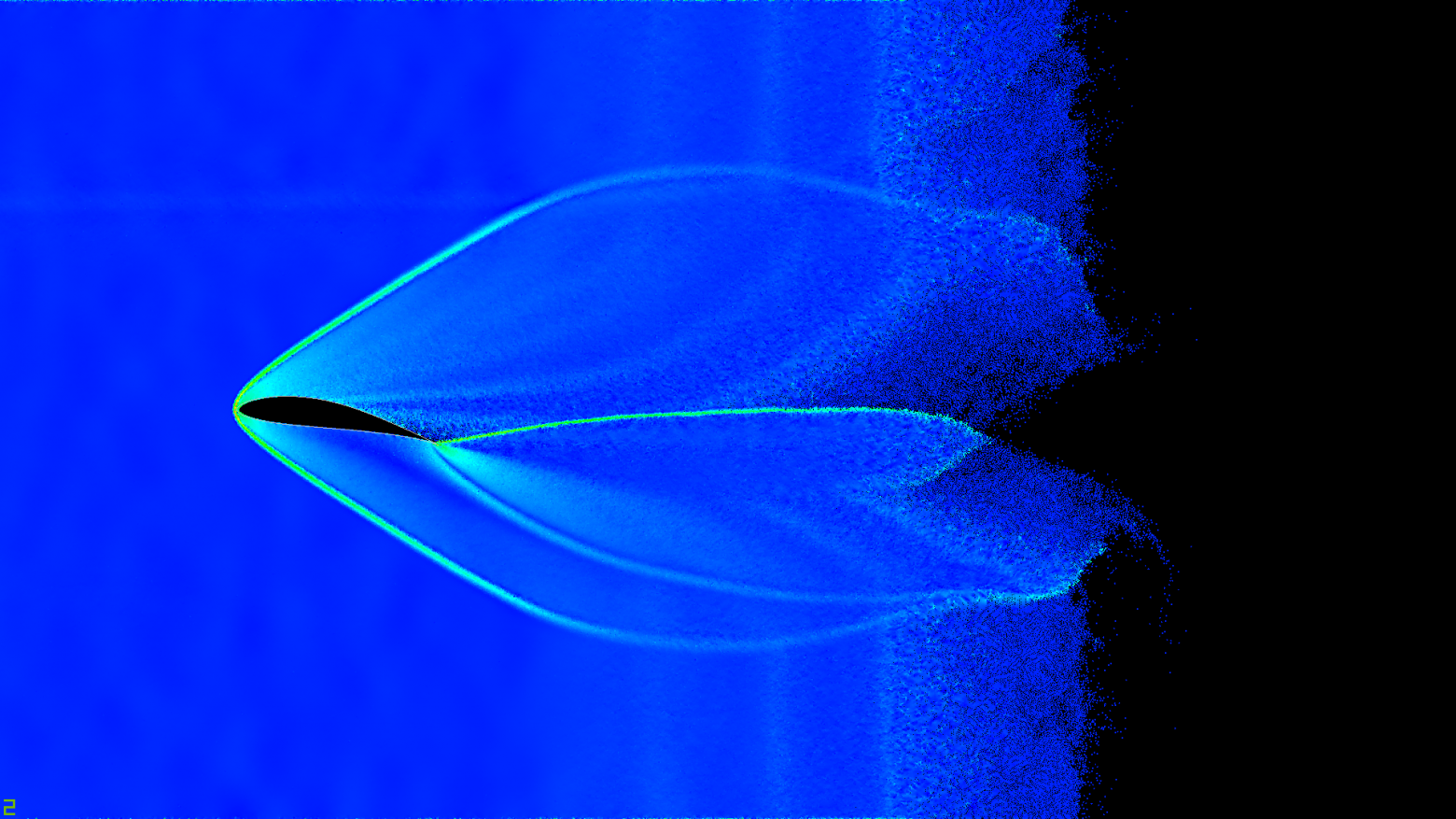
Тепловая карта ускорений частиц
Архитектура симулятора
Давайте теперь рассмотрим, как устроен симулятор. Приложение состоит из двух независимых модулей:
- Рендерер текущего состояния.
- Модуль симуляции на CPU или CUDA.
Модули слабо связаны друг с другом и напрямую не зависят. Существует возможность проводить симуляцию в оффлайн режиме и рендерить результаты позднее. В CUDA-версии демонстрации рендеринг, что на видео в начале статьи, происходит каждые 16 шагов.
Фазовое пространство
Концепция фазового пространства широко используется в различного рода симуляциях. Основная идея состоит в том, что все переменные системы, такие как позиция, ориентация, импульсы, и т.д., упаковываются в один большой вектор. Этот многомерный вектор обозначает точку в так называемом фазовом пространстве. Сама симуляция есть не что иное как движение точки через это пространство.
Такое представление очень удобно, потому что практически любую симуляцию можно выразить в таком виде. Движение точки состояния как правило выражается через обыкновенное дифференциальное уравнение первого порядка (Ordinary Differential Equation, ODE). Это уравнение имеет вид , где
— это позиция точки в фазовом пространстве, а
— чёрный ящик, способный определить скорость изменения состояния. Зная
и
, можно посчитать следующее значение
.
Вне зависимости от того, как работает f, симуляция — это всего лишь процесс численного интегрирования.
Подробнее по теме фазового пространства можно ознакомиться в разделах 'Differential Equation Basics' and 'Particle Dynamics' курса https://www.cs.cmu.edu/~baraff/sigcourse/
На канале 3Blue1Brown также доступны отличные материалы: 
https://www.youtube.com/playlist?list=PLZHQObOWTQDNPOjrT6KVlfJuKtYTftqH6
Интегратор
После различных экспериментов я решил остановиться на самом грубом, но в то же время самом простом — методе Эйлера (Forward Euler). Я пробовал использовать метод Рунге-Кутты 4-го порядка (RK4), в том числе и с адаптивным шагом, но для конкретно этого сценария больше подошёл метод Эйлера. Преимущество RK4 в том, что он позволяет делать огромные временные шаги ценой четырёхкратного увеличения вычислений, что в некоторых сценариях оправданно. В моём же случае оказалось, что я привязан к малым временным шагам, из-за необходимости избегать туннелирования частиц друг через друга. Кстати, как работают интеграторы с адаптивным временным шагом опираясь на ошибку, можно почитать в 'Differential Equation Basics' lecture notes, section 3, 'Adaptive Stepsizes'.
В данной симуляции, чтобы свести туннелирования к минимуму, адаптивность шага достигается следующим эвристическим правилом. Симулятор находит самую быструю частицу и вычисляет время, за которое эта частица пройдёт расстояние равное радиусу. Это время используется как временной шаг на текущей итерации.
float CSimulationCpu::ComputeMinDeltaTime(float requestedDt) const
{
auto rad = m_state.particleRad;
auto velBegin = m_curOdeState.cbegin() + m_state.particles;
auto velEnd = m_curOdeState.cend();
return std::transform_reduce(std::execution::par_unseq, velBegin, velEnd, requestedDt, [](const auto t1, const auto t2)
{
return std::min(t1, t2);
}, [&](const auto& v)
{
auto vel = glm::length(v);
auto radDt = rad / vel;
return radDt;
});
}
float CSimulationCpu::Update(float dt)
{
dt = ComputeMinDeltaTime(dt);
m_odeSolver->NextState(m_curOdeState, dt, m_nextOdeState);
ColorParticles(dt);
m_nextOdeState.swap(m_curOdeState);
return dt;
}Вычисление производной состояния
Теперь перейдём к сердцу симулятора — определению той самой функции f, упомянутой в параграфе “Фазовое пространство”. Ниже приведён высокоуровневый код солверов производной для CPU и CUDA версий. Стоит отметить, что CPU версия исторически появилась раньше, так как на ней было проще отладить математику. В CUDA версии появились некоторые улучшения и оптимизации, но суть осталась та же. Отличие состоит в переупорядочивании частиц. Подробнее в разделе “Реордеринг частиц”.
//CPU-версия
void CDerivativeSolver::Derive(const OdeState_t& curState, OdeState_t& outDerivative)
{
ResetForces();
BuildParticlesTree(curState);
ResolveParticleParticleCollisions(curState);
ResolveParticleWingCollisions(curState);
ParticleToWall(curState);
ApplyGravity();
BuildDerivative(curState, outDerivative);
}
//CUDA-версия
void CDerivativeSolver::Derive(const OdeState_t& curState, OdeState_t& outDerivative)
{
BuildParticlesTree(curState);
ReorderParticles(curState);
ResetParticlesState();
ResolveParticleParticleCollisions();
ResolveParticleWingCollisions();
ParticleToWall();
ApplyGravity();
BuildDerivative(curState, outDerivative);
}Поиск столкновений между частицами
Как вы уже, наверное, могли понять, поиск столкновений — это краеугольный камень всех расчётов. В видео в самом начале статьи участвует 2’097’152 частиц. Среди всего этого количества нужно каким-то быстрым образом найти все сталкивающиеся пары. Интересно, но у этой проблемы нет однозначно правильного решения. Любой способ — это набор компромиссов и допущений.
Один из возможных вариантов — это использование Uniform Grid, то есть однородной сетки из ячеек на подобии шахматной доски. Одна из реализаций для GPU описана в статье “Chapter 32. Broad-Phase Collision Detection with CUDA”.

Каждая ячейка пространства содержит в себе список объектов (изображение Tero Karras, NVIDIA Corporation)
В этом случае, поиск столкновений в среднем будет занимать порядка . Каждой частице нужно обойти списки в 9 (3x3) или 27 (3x3x3) ячейках для 2D или 3D случая соответственно. Ещё один приятный плюс структуры — это относительная простота распараллеливания её построения. Память под списки можно выделить либо заранее в виде массива, и вычислять выходной индекс через атомарный инкремент, либо строить классический RCU lock-free односвязный список. Nvidia в своих видеокартах уже давно добавила поддержку кучи, поэтому можно вызвать malloc()/free() прямо в device коде, выделяя и освобождая элементы списков.
CppCon 2017: Fedor Pikus “Read, Copy, Update, then what? RCU for non-kernel programmers”
Однако, у этой структуры есть следующий ряд фундаментальных ограничений:
- Множество значений координат ограничено размером самой сетки.
- Близкие ячейки в евклидовом пространстве как правило расположены далеко в адресном пространстве RAM/VRAM, не разделяя единую кэш-линию, что создаёт дополнительную нагрузку на шину памяти.
- При низкой плотности объектов или малом их количестве структура данных начинает потреблять больше памяти, чем сами данные.
- Возможно появление чрезмерно длинных списков при большой плотности объектов.
- В связи с аппаратными особенностями планирования потоков на GPU, некоторые lock-free структуры не способны работать корректно (https://youtu.be/86seb-iZCnI?t=2311, ссылка с таймкодом).
Другой вариант, который я решил использовать в этой симуляции — это BVH-дерево на основе Z-кривой. Я наткнулся на эту довольно любопытную структуру данных, когда искал альтернативы однородной сетке.
Первая важная особенность этой структуры данных — в её основе лежит фрактальная Z-кривая, она же Кривая Мортона.

Фрактальная Z-кривая (изображение Wikipedia)

Принцип вычисления индекса на кривой — чередование битов координат
(изображение Wikipedia)
Задача этой кривой, как и любой другой space-filling curve, состоит в том, чтобы упаковать пространства высших размерностей в одномерное пространство. Если присвоить каждому объекту в 2D/3D пространстве индекс на любой такой кривой, а затем отсортировать все объекты по этому индексу, то мы увидим, что объекты, расположенные близко в геометрическом пространстве, как правило будут лежать близко и в одномерном пространстве. Это свойство позволяет существенно снизить нагрузку на шину памяти. Кстати, если вам нужно обрабатывать изображения, выполняя различные свёрточные операции и применяя фильтры, возможно, вам стоит хранить пиксели в виде одной из такой кривых, а не в виде матрицы.
Вторая главная особенность этой структуры данных состоит в том, что построение отношений между узлами дерева выполняется в параллельном режиме. В процессе построения связей потоки никак не общаются друг с другом, что позволяет достичь максимального уровня параллелизма. Это и не удивительно, потому что подход был предложен инженером Tero Karras из Nvidia, специально для решения задач поиска столкновений на видеокартах.
Детально алгоритм описан в статье “Maximizing Parallelism in the Construction of BVHs, Octrees, and k-d Trees”.
Краткое изложение:
- Обход дерева: https://developer.nvidia.com/blog/thinking-parallel-part-ii-tree-traversal-gpu/
- Построение дерева: https://developer.nvidia.com/blog/thinking-parallel-part-iii-tree-construction-gpu/
В сухом остатке, алгоритм следующий. Для каждого из N объектов запускается отдельный поток, который вычисляет bounding box и, на основе его центра, вычисляет код Мортона (индекс на Z-кривой). После этого этапа боксы сортируются в порядке возрастания кода.

Формирование кодов Мортона (изображение Tero Karras, NVIDIA Corporation)
Затем инициализируются узлы дерева. В частности, ещё до построения самого дерева, известно, что для N листьев будет существовать N-1 промежуточных узлов. Соответственно, необходимые аллокации и первичные инициализации осуществляются на этом шаге. Далее наступает самый хитроумный этап. Алгоритм ищет различия в кодах, двигаясь от старших бит к младшим. Наличие разницы сигнализирует о том, что нужно сформировать промежуточный узел. Ниже на рисунках представлены однопоточная версия алгоритма и его распараллеленная версия.

Последовательный алгоритм построения префиксного дерева (изображение Tero Karras, NVIDIA Corporation)

Параллельный алгоритм построения префиксного дерева (изображение Tero Karras, NVIDIA Corporation)
После того, как связи между узлами выстроены, начинается этап формирования BVH-структуры.
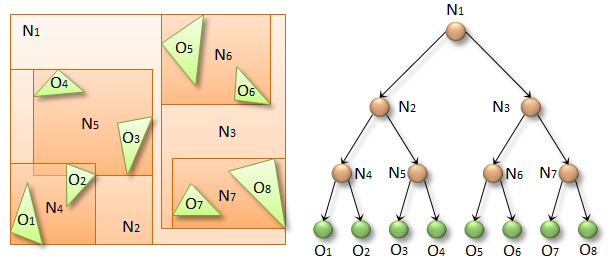
BVH-структура (изображение Tero Karras, NVIDIA Corporation)
N потоков стартуют с листьев и, поднимаясь к корню, обновляют боксы промежуточных узлов. Так как не определено, какой из детей придёт к родителю первым, то в промежуточных узлах хранится специальный флаг, изначально установленный в ноль. Оба ребёнка с помощью атомарной функции atomicExch() устанавливают флаг в 1. Функция возвращает старое значение, которое было до модификации. Если ребёнку функция вернула 0, то значит он первый. Это также означает, что текущему потоку нельзя модифицировать бокс родителя, потому что бокс его сиблинга может быть ещё не готов. На этом этапе поток завершает своё исполнение. Если же ребёнку функция вернула 1, то можно смело модифицировать родительский бокс, объединяя боксы обоих сиблингов, и снова повторить процесс.
После этого этапа дерево готово к осуществлению запросов.
Реакция на столкновения
В симуляции существует два типа столкновений “частица-частица” и “частица-сегмент профиля”.
Реакция “частица-частица” использует факт того, все объекты уже сохранены в дереве, поэтому существует частная процедура “рефлексивного” обхода, когда листья ищут столкновения друг с другом. Эта оптимизация была предложена Tero Karras. Особенность процедуры в том, что она распознаёт столкновения A-B и B-A как одно и то же столкновение, поэтому оно детектируется только один раз. Для этого при построении дерева вводится дополнительная информация. В промежуточных узлах хранится индекс самого правого листа (rightmost leaf), до которого можно добраться. Например, на рисунке выше rightmost(N2) = 4, а rightmost(N3) = 8. Когда поток, связанный с листом, скажем, O6, будет опускаться от корня, он обратится к промежуточному узлу N2. Благодаря переменной rightmost, он увидит, что лист O6 недостижим из поддерева N2. В этом случае поток O6 должен проигнорировать всё поддерево N2. Однако, потоки, связанные с листьями из поддерева N2, будут проверять поддерево N3. В конечном итоге, если столкновение с O6 и существует, то об этом сообщит только один поток, и он будет из поддерева N2.
Для частной процедуры рефлексивного обхода прототип функции выглядит следующим образом:
template<typename TDeviceCollisionResponseSolver, size_t kTreeStackSize>
void CMortonTree::TraverseReflexive(const TDeviceCollisionResponseSolver& solver);Для случая “частица-сегмент профиля” используется универсальная версия:
template<typename TDeviceCollisionResponseSolver, size_t kTreeStackSize>
void CMortonTree::Traverse(const thrust::device_vector<SBoundingBox>& objects, const TDeviceCollisionResponseSolver& solver);Здесь TDeviceCollisionResponseSolver — это объект, который должен реализовать следующий интерфейс:
struct Solver
{
struct SDeviceSideSolver
{
...
__device__ SDeviceSideSolver(...);
__device__ void OnPreTraversal(TIndex curId);
__device__ void OnCollisionDetected(TIndex leafId);
__device__ void OnPostTraversal();
};
Solver(...);
__device__ SDeviceSideSolver Create();
}; Для каждого тестируемого на столкновение объекта, или листа в случае рефлексивного подхода, создаётся отдельный поток. Каждый поток создаёт свой солвер через фабричную функцию Create(). Далее вызывается метод OnPreTraversal, куда передаётся индекс тестируемого объекта. Если бокс текущего тестируемого объекта перекрыл бокс какого-то листа, вызывается функция OnCollisionDetected с индексом листа. Эта функция отвечает за расчёт физики. После обхода дерева вызывается OnPostTraversal.
Такой формат разрешения коллизий появился неслучайно. С самого начала я реализовал его по-другому. Я разделил обход дерева и вычисление физики на две различные стадии, как это сделал Tero Karras. Однако я столкнулся с проблемой построения списков найденных столкновений. Я попробовал сохранять информацию о коллизиях в виде матрицы NxO, где N — количество тестируемых объектов, O — максимальный размер списка. Но я отказался от этой идеи, потому что при определенных сценариях быстро заканчивалось место в списках. А это в свою очередь создавало различные физические артефакты. К тому же я обратил внимание, что профилировщик сигнализировал о неэффективной работе с памятью (coalesced memory access). Поэтому я решил попробовать подход без списков, который был описан выше. К моему удивлению, способ оказался немного быстрее и без артефактов.
struct SParticleParticleCollisionSolver
{
struct SDeviceSideSolver
{
CDerivativeSolver::SIntermediateSimState& simState;
TIndex curIdx;
float2 pos1;
float2 vel1;
float2 totalForce;
float totalPressure;
__device__ SDeviceSideSolver(CDerivativeSolver::SIntermediateSimState& state) : simState(state)
{
}
__device__ void OnPreTraversal(TIndex curLeafIdx)
{
curIdx = curLeafIdx;
pos1 = simState.pos[curLeafIdx];
vel1 = simState.vel[curLeafIdx];
totalForce = make_float2(0.0f);
totalPressure = 0.0f;
}
__device__ void OnCollisionDetected(TIndex anotherLeafIdx)
{
const auto pos2 = simState.pos[anotherLeafIdx];
const auto deltaPos = pos2 - pos1;
const auto distanceSq = dot(deltaPos, deltaPos);
if (distanceSq > simState.diameterSq || distanceSq < 1e-8f)
return;
const auto vel2 = simState.vel[anotherLeafIdx];
auto dist = sqrtf(distanceSq);
auto dir = deltaPos / dist;
auto springLen = simState.diameter - dist;
auto force = SpringDamper(dir, vel1, vel2, springLen);
auto pressure = length(force);
totalForce += force;
totalPressure += pressure;
atomicAdd(&simState.force[anotherLeafIdx].x, -force.x);
atomicAdd(&simState.force[anotherLeafIdx].y, -force.y);
atomicAdd(&simState.pressure[anotherLeafIdx], pressure);
}
__device__ void OnPostTraversal()
{
atomicAdd(&simState.force[curIdx].x, totalForce.x);
atomicAdd(&simState.force[curIdx].y, totalForce.y);
atomicAdd(&simState.pressure[curIdx], totalPressure);
}
};
CDerivativeSolver::SIntermediateSimState simState;
SParticleParticleCollisionSolver(const CDerivativeSolver::SIntermediateSimState& state) : simState(state)
{
}
__device__ SDeviceSideSolver Create()
{
return SDeviceSideSolver(simState);
}
};
void CDerivativeSolver::ResolveParticleParticleCollisions()
{
m_particlesTree.TraverseReflexive<SParticleParticleCollisionSolver, 24>(SParticleParticleCollisionSolver(m_particles.GetSimState()));
CudaCheckError();
}Во время отладки я обратил внимание, что при высокой плотности частиц, функция OnCollistionDetected как правило вызывается для одних и тех же аргументов среди потоков одного варпа. Типовой сценарий был следующий: если в какой-то области пространства есть частицы A, B, C и D, которые в указанном порядке расположены на Z кривой, то приблизительно происходило вот что:
| lock-step # | Thread #1 | Thread #2 | Thread #3 |
|---|---|---|---|
| 1 | OnCollisionDetected A <-> C |
OnCollisionDetected B <-> C |
OnCollisionDetected C <-> D |
| 2 | OnCollisionDetected A <-> D |
OnCollisionDetected B <-> D |
INACTIVE |
| 3 | OnPostTraversal(1) | OnPostTraversal(2) | OnPostTraversal(3) |
Как видно из таблицы, на шаге 1 и 2 потоки #1 и #2 выполняли атомарные обращения atomicAdd с одними и тем же частицам C и D в процессе работы функции OnCollistionDetected. Это создаёт дополнительную нагрузку на atomic транзакции.
Начиная с архитектуры Volta, Nvidia добавила в чипы поддержку новых warp-vote инструкций. С помощью инструкции match_any поток может опросить весь warp, получив битовую маску потоков, у которых значение запрашиваемой переменной имеет такое же значение.
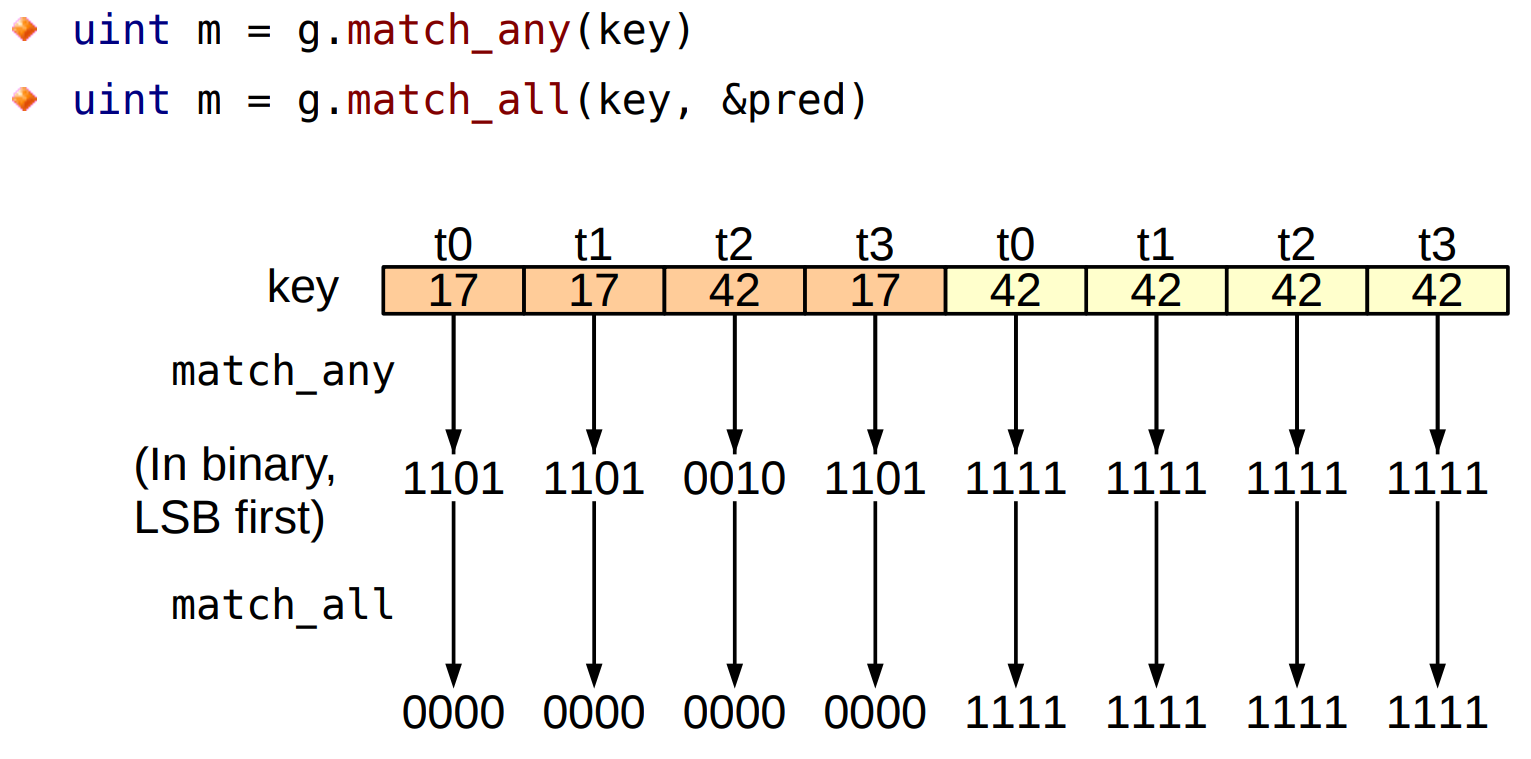
Результат работы match_any и match_all для двух кооперативных групп
Коммуникация внутри варпа тоже стала удобнее, потому что появились новые warp shuffle функции с поддержкой маски потоков.

Warp-wide редукция с помощью старых функций без маски
Благодаря этим функциям, потоки перед обращением в глобальную память могут сгруппироваться по признаку общего выходного адреса. Далее эта группа должна выполнить суммирование на уровне регистров SM и уже после этого только один поток обращается в глобальную память. К сожалению, на моём домашнем Pascal (1080 Ti) таких инструкций нет, поэтому я решил попробовать их проэмулировать. Увы, никакого прироста, как и замедления это не дало. Профилировка показала, что хоть нагрузка на atomic транзакции и упала в несколько раз, существенно возросла нагрузка на Arithmetic Workload и увеличилось количество регистров на поток. Заняться разработкой на чипах с Volta или Turing пока не представилось возможным. Хотя, мне всё же удалось протестировать симуляцию на RTX 2060 и найти баг, связанной с atomic операцией. Об этом в разделе “Барьер памяти”.
Другие оптимизации и дополнения
В данном разделе мне бы хотелось рассказать о некоторых отличиях от оригинального алгоритма, которые дали дополнительный прирост в производительности, а также некоторые комментарии по особенностям реализации.
SoA
Structure of Arrays — одна из техник, которая позволяет ускорить доступ к памяти в определённых ситуациях.
При работе с деревом на любом из этапов как правило не требуется полный набор атрибутов. А значит вместо того, чтобы хранить каждый узел в виде структуры, всё дерево хранится в виде SoA:
typedef uint32_t TIndex;
struct STreeNodeSoA
{
const TIndex leafs;
int* __restrict__ atomicVisits;
TIndex* __restrict__ parents;
TIndex* __restrict__ lefts;
TIndex* __restrict__ rights;
TIndex* __restrict__ rightmosts;
SBoundingBox* __restrict__ boxes;
const uint32_t* __restrict__ sortedMortonCodes;
};То же самое касается и внутреннего состояния солвера производной состояния:
struct SIntermediateSimState
{
const TIndex particles;
const float particleRad;
const float diameter;
const float diameterSq;
float2* __restrict__ pos;
float2* __restrict__ vel;
float2* __restrict__ force;
float* __restrict__ pressure;
}; В то же время, массив bounding box’ов нет смысла хранить в SoA стиле, потому что во всех сценариях необходимы обе точки. Поэтому боксы хранятся в виде Array of Structures (AoS):
struct SBoundingBox
{
float2 min;
float2 max;
};
struct SBoundingBoxesAoS
{
const size_t count;
SBoundingBox* __restrict__ boxes;
}; Реордеринг частиц
Так как текущая реализация не строит списки столкновений, а разрешает коллизии прямо на месте, то возникает следующая проблема. После присвоения кодов Мортона центрам боксов, выполняется сортировка самих боксов. Однако остальные параметры частиц остаются неотсортированными. Если в процессе обхода дерева продолжить обращаться к данным в исходном порядке, то мы получаем uncoalesced memory access.
Такой паттерн доступа очень медленно работает на GPU. Для восстановления coalesced memory access, позиции и скорости частиц тоже упорядочиваются вдоль кривой. А после выполнения всех расчётов, силы и давления как выходные величины возвращаются к исходному порядку. Идея не нова и была позаимствована из уже упомянутого доклада SpaceX: https://youtu.be/vYA0f6R5KAI?t=1939 (ссылка с таймкодом).
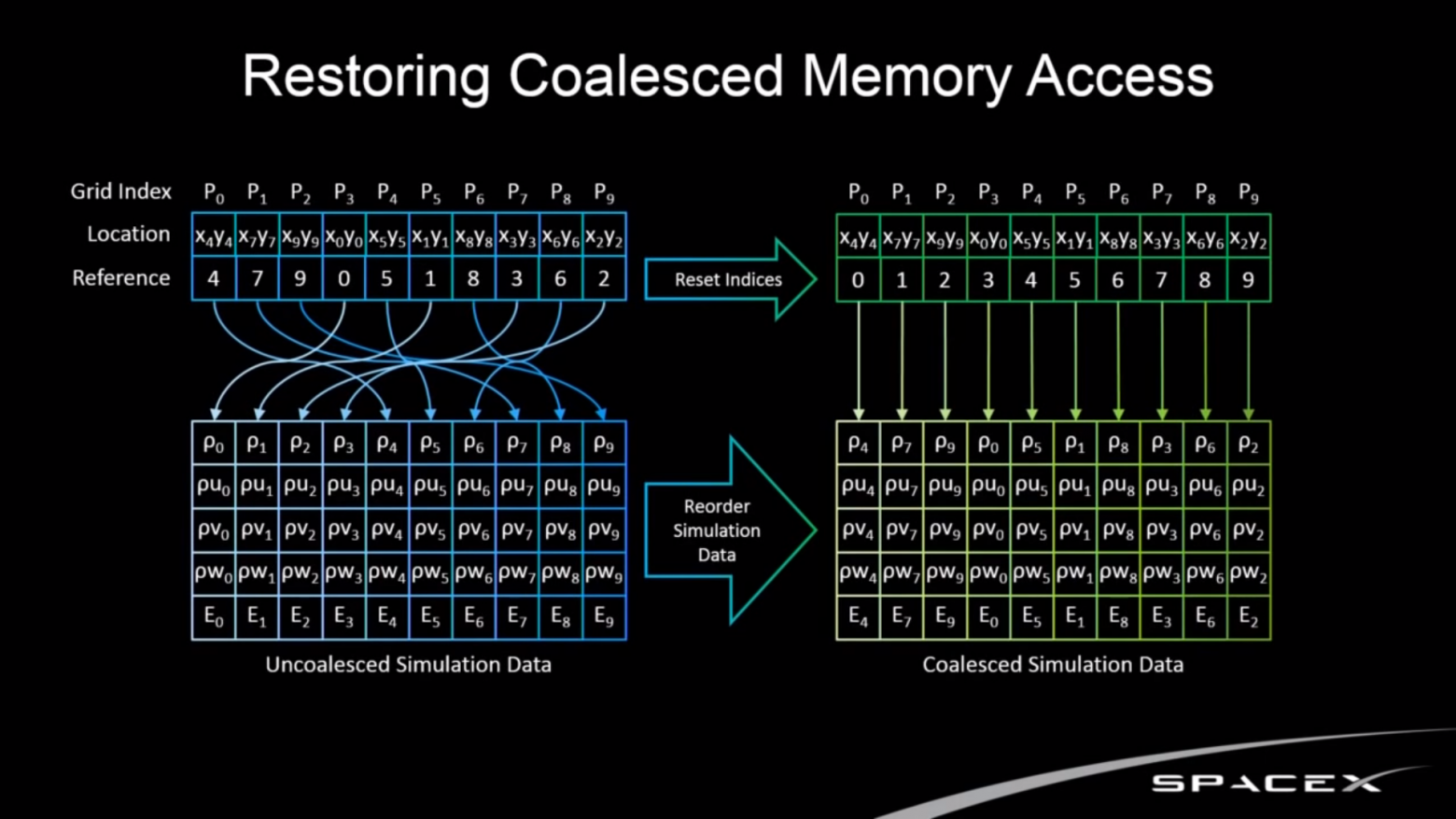
Восстановление объединённого доступа к памяти (изображение SpaceX)
Такая оптимизация даёт 50% прироста производительности: с 8 FPS до 12 FPS для двух миллионов частиц.
UPD: во избежание недопониманий уточню, что между кадрами происходит 16 шагов симуляции, то есть после этой оптимизации пиковая производительность достигла 192 шагов в секунду. Зачем нужно было так делать, я развёрнуто ответил в комментарии.
Стек в Shared Memory
Оригинальная статья приводит пример реализации, где стек для обхода дерева реализуется в виде локального массива в скоупе функции. Проблема этого подхода в том, что задействуется локальная память потока — область в глобальной памяти. А значит SM начинает выполнять долгие транзакции на чтение и запись, которые ко всему прочему могут оказаться ещё uncoalesced. Суть данной оптимизации в том, чтобы использовать сверхбыструю Shared Memory на кристалле самого Streaming Multiprocessor’а.
__device__ void traverseIterative( CollisionList& list,
BVH& bvh,
AABB& queryAABB,
int queryObjectIdx)
{
// Allocate traversal stack from thread-local memory,
// and push NULL to indicate that there are no postponed nodes.
NodePtr stack[64]; //<---------------------------- Проблемное место
NodePtr* stackPtr = stack;
*stackPtr++ = NULL; // push
// Traverse nodes starting from the root.
NodePtr node = bvh.getRoot();
do
{
// Check each child node for overlap.
NodePtr childL = bvh.getLeftChild(node);
NodePtr childR = bvh.getRightChild(node);
bool overlapL = ( checkOverlap(queryAABB,
bvh.getAABB(childL)) );
bool overlapR = ( checkOverlap(queryAABB,
bvh.getAABB(childR)) );
// Query overlaps a leaf node => report collision.
if (overlapL && bvh.isLeaf(childL))
list.add(queryObjectIdx, bvh.getObjectIdx(childL));
if (overlapR && bvh.isLeaf(childR))
list.add(queryObjectIdx, bvh.getObjectIdx(childR));
// Query overlaps an internal node => traverse.
bool traverseL = (overlapL && !bvh.isLeaf(childL));
bool traverseR = (overlapR && !bvh.isLeaf(childR));
if (!traverseL && !traverseR)
node = *--stackPtr; // pop
else
{
node = (traverseL) ? childL : childR;
if (traverseL && traverseR)
*stackPtr++ = childR; // push
}
}
while (node != NULL);
}template<typename TDeviceCollisionResponseSolver, size_t kTreeStackSize, size_t kWarpSize = 32>
__global__ void TraverseMortonTreeKernel(const CMortonTree::STreeNodeSoA treeInfo, const SBoundingBoxesAoS externalObjects, TDeviceCollisionResponseSolver solver)
{
const auto threadId = blockIdx.x * blockDim.x + threadIdx.x;
if (threadId >= externalObjects.count)
return;
const auto objectBox = externalObjects.boxes[threadId];
const auto internalCount = treeInfo.leafs - 1;
__shared__ TIndex stack[kTreeStackSize][kWarpSize]; //Тот самый стек
unsigned top = 0;
stack[top][threadIdx.x] = 0;
auto deviceSideSolver = solver.Create();
deviceSideSolver.OnPreTraversal(threadId);
while (top < kTreeStackSize) //top == -1 also covered
{
auto cur = stack[top--][threadIdx.x];
if (!treeInfo.boxes[cur].Overlaps(objectBox))
continue;
if (cur < internalCount)
{
stack[++top][threadIdx.x] = treeInfo.lefts[cur];
if (top + 1 < kTreeStackSize)
stack[++top][threadIdx.x] = treeInfo.rights[cur];
else
printf("stack size exceeded\n");
continue;
}
deviceSideSolver.OnCollisionDetected(cur - internalCount);
}
deviceSideSolver.OnPostTraversal();
}Использование Shared Memory позволяет достичь прироста на 43%: с 14 FPS до 20 FPS. Подробнее о доступных типах памяти можно почитать в официальной документации:
https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html#device-memory-accesses
Барьер памяти
Когда я разрабатывал симулятор, я пользовался исключительно одной видеокартой — 1080 Ti поколения Pascal. Пользоваться другими в целях разработки, к сожалению, возможности не было. Но у меня была возможность просить трёх моих знакомых запустить приложение на их игровых ноутбуках с новой на тот момент 20-й серией чипов. Все три ноутбука выдавали изображения с вот такими артефактами.

Артефакт на 20-й RTX серии. Позиции и размер артефактов каждый шаг менялись.
Сначала я думал, что это проблема визуализации, но нигде не мог найти ошибку. Проверка кода самой симуляции тоже не дала результатов. Осознание пришло через полгода после просмотра этого доклада:
Доклад об атомиках и барьерах памяти.
Половина доклада посвящена идее барьеров памяти и почему они важны при работе с atomic-операциями и lock-free структурами. Дело в том, что процессоры имеют тенденцию переупорядочивать выполнение инструкций (Out-of-order execution), но при этом отслеживая и сохраняя зависимости между ними, чтобы гарантировать корректность. В случае с lock-free структурами для процессоров зависимость не очевидна. Поэтому, нужны барьеры памяти, которые подсказывают процессору, что инструкции не могут быть переупорядочены через барьер. Каждая платформа реализует барьеры по-своему, но, к счастью, разработчики стандарта C++ смогли построить наиболее общую модель. Подробное описание каждой семантики барьеров доступно в документации по std::memory_order.
__device__ void CMortonTree::STreeNodeSoA::BottomToTopInitialization(size_t leafId)
{
auto cur = leafs - 1 + leafId;
auto curBox = boxes[cur];
while (cur != 0)
{
auto parent = parents[cur];
//1. Опасная atomic операция
auto visited = atomicExch(&atomicVisits[parent], 1);
if (!visited)
return;
TIndex siblingIndex;
SBoundingBox siblingBox;
TIndex rightmostIndex;
TIndex rightmostChild;
auto leftParentChild = lefts[parent];
if (leftParentChild == cur)
{
auto rightParentChild = rights[parent];
siblingIndex = rightParentChild;
rightmostIndex = rightParentChild;
}
else
{
siblingIndex = leftParentChild;
rightmostIndex = cur;
}
siblingBox = boxes[siblingIndex];
rightmostChild = rightmosts[rightmostIndex];
SBoundingBox parentBox = SBoundingBox::ExpandBox(curBox, siblingBox);
boxes[parent] = parentBox;
rightmosts[parent] = rightmostChild;
cur = parent;
curBox = parentBox;
//2. Спасительный барьер памяти.
//Следующая итерация гарантированно увидит результаты всех записей
__threadfence();
}
}Моя ошибка была в том, что я не использовал никаких барьеров памяти в коде, который строит BVH дерево, но при этом активно использует атомарный флаг. Интересно, что оригинальная статья также не использует никаких барьеров. Скорее всего, помимо новой SIMT модели (разделы Volta SIMT Model и Starvation-Free Algorithms) Nvidia добавила в новые архитектуры начиная с Volta более агрессивную реализацию уже упомянутой Out-of-order execution. Как следствие, операции, которые должны были выполняться до atomicExch(), т.е. ещё на предыдущей итерации цикла, на Turing исполняются уже после. В результате такого агрессивного реордеринга инструкций, второй ребёнок, приходя к родителю думает, что его сиблинг уже вычислил и сохранил бокс в общую память, а на самом деле нет. В результате получается data race.
thrust::device_vector
Я слишком поздно заметил, что thurst::device_vector работает в синхронном режиме. Этот контейнер в своём конструкторе и в методе resize() выполняет полную синхронизацию с GPU через cudaDeviceSynchronize(). Видимо, разработчики руководствовались следующими рассуждениями. Раз вектор на видеокарте, то и конструкторы элементов нужно тоже вызывать на видеокарте. Но так как конструкторы могут кидать исключения, нужно дождаться их исполнения, чтобы словить все исключения. Единственный доступный способ для них — полная синхронизация. Ещё одна из обнаруженных проблем — редукция (reduce, sum, min, max) тоже синхронная, так как возвращает результат на хост. Библиотека Cuda UnBound (CUB) в этом плане куда продуманнее. Кстати, недавно она вошла в состав thrust как бэкенд, хотя раньше её нужно было скачивать отдельно.
Результаты профилировки
Наконец, подробный отчёт о том, что происходит во время расчёта каждого шага для двух миллионов частиц.
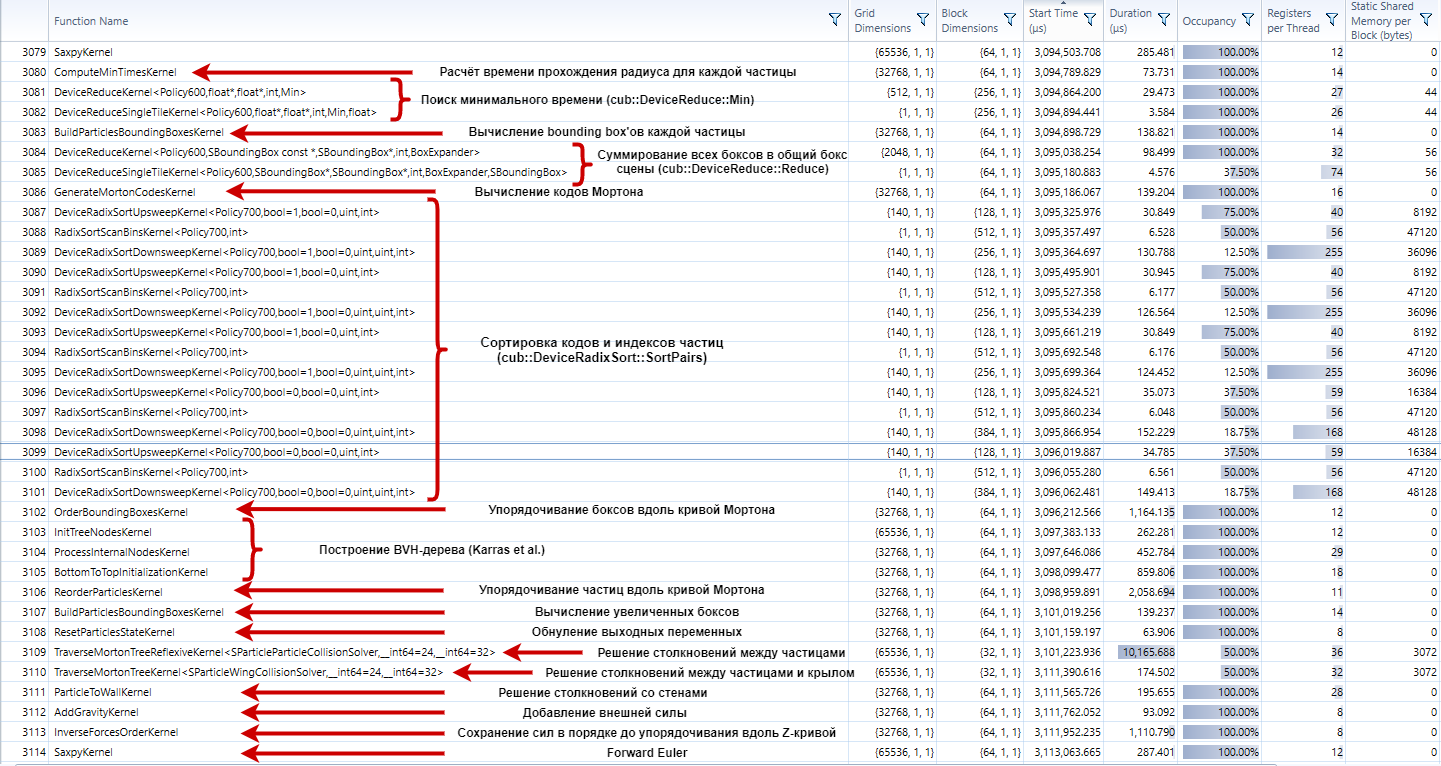
Картинка кликабельна, можно посмотреть в высоком разрешении
Заключение
Когда я брался за этот проект, я всего лишь хотел использовать GPU как мини-суперкомпьютер, чтобы проверить жизнеспособность модели Ньютона. В итоге задача оказалась куда интереснее и плодотворнее, чем ожидалось. Симуляция показала “эффект пушечного ядра”, а сама работа над проектом вылилась в исследование и долгие часы работы в APOD режиме.
Надеюсь, что описанный в этой статье опыт, а также предложенные решения проблем, помогут вам в ваших проектах, пускай даже не связанные с GPU.
Если вы хотели бы начать изучать CUDA, но не знаете, с чего начать, на Youtube есть отличный курс от Udacity “Intro to Parallel Programming”. Рекомендую к ознакомлению.
https://www.youtube.com/playlist?list=PLAwxTw4SYaPnFKojVQrmyOGFCqHTxfdv2
Напоследок, ещё несколько видео симуляций:
CPU-версия, 8 потоков, 131'072 частиц
CUDA-версия, 4.2М частиц, 30 минут симуляции