Сортировка — такая же «вечная» тема для алгоритмистов, как любовь — для поэтов. Казалось бы, новое слово в этой области сказать трудно, а поди же ты — продолжают придумывать новые алгоритмы сортировок (TimSort...) Есть, однако, базовые факты, которые знает каждый приличный студент. Известно, к примеру, что универсальный алгоритм сортировки не может быть быстрее O(n*log(n)). Такой показатель производительности имеет знаменитая QuickSort (придуманная в 1960-м году Хоаром), а также сортировка слиянием (Фон Неймана) и пирамидальная сортировка. Что же касается элементарных алгоритмов («пузырек», «вставки», «выбор»), то их показатель существенно хуже — O(n^2). Но всегда ли QuickSort является «абсолютным чемпионом»?
Ведь кроме показателя производительности есть и другие характеристики, зачастую — не менее важные. Один из них — естественность. Что это такое? Сортировка называется естественной, если она выполняется быстрее в том случае, когда массив уже почти отсортирован. А какой массив можно считать «почти отсортированным»? Вот два массива, состоящие из одних и тех элементов:
{1,2,9,3,4,5,7,6,8,10} и {9,1,6,3,10,5,4,2,8,7}
Даже на глаз видно, что первый массив более упорядочен (только 9 и 7 стоят «не на месте»). Тогда как во втором массиве числа перемешаны хаотически. Что же является мерой упорядоченности? Ответ известен — количество инверсий. Пара элементов A[i] и A[j] при j > i составляют инверсию, если A[j] < A[i]. (В этой заметке целью сортировки всегда является упорядочение по возрастанию).
Теперь можно дать точное определение: сортировка называется естественной, если время ее работы снижается при снижении количества инверсий в исходном массиве.
Естественность — достаточно «редкий фрукт» в мире сортировок — ни QuickSort ни сортировка Шелла не обладают этим свойством, увы. Но есть один алгоритм, который, можно сказать, является абсолютно естественным — это сортировка вставками. Хотя этот алгоритм известен каждому культурному человеку, позволю себе кратко повторить его суть.
Сортируемый массив просматривается один раз от начала к концу. Как только обнаруживается, что i-й и (i-1)-элементы образуют инверсию, i-й элемент «закидывается» назад (что достигается сдвигом нужного отрезка начала массива вправо на одну позицию). Из этого описания понятно, что если в массиве мало инверсий, алгоритм «пролетит» по массиву очень быстро. Если инверсий нет совсем, то алгоритм завершится за время O(n). А вот QuickSort в этом случае будет долго и утомительно выбирать разделяющий элемент, делить уже упорядоченный массив на отрезки и т.п. Но при наличии большого количества инверсий ситуация, разумеется, будет обратной: производительность сортировки вставками упадет до O(n^2), а QuickSort будет чемпионом — O(n*log(n)).
Сложившаяся ситуация порождает естественный с моей точки зрения вопрос: при каком количестве инверсий перевешивает естественность и сортировка вставками работает быстрее QuickSort?
Для ответа на этот вопрос я провел серию вычислительных экспериментов. Суть их состояла в следующем. Брались массивы целых чисел размером от 3000 до 30000 элементов, в них вносилось некоторое количество инверсий, затем массивы сортировались вставками и быстрой сортировкой. Замерялось время сортировки (в системных тиках). Для усреднения каждая сортировка повторялась 10 раз. Результаты оказались следующими:

На картинке представлены зависимости времени сортировки от количества внесенных инверсий. Малиновая серия — это, естественно, QuickSort, а синяя — сортировка вставками. Для размера массива 30 тыс. элементов, до примерно 400 тыс. инверсий «побеждает естественность». Для менее упорядоченных массивов уже выгоднее QuickSort.
А на следующей картинке приведена эмпирическая зависимость критического количества инверсий от размера массива.
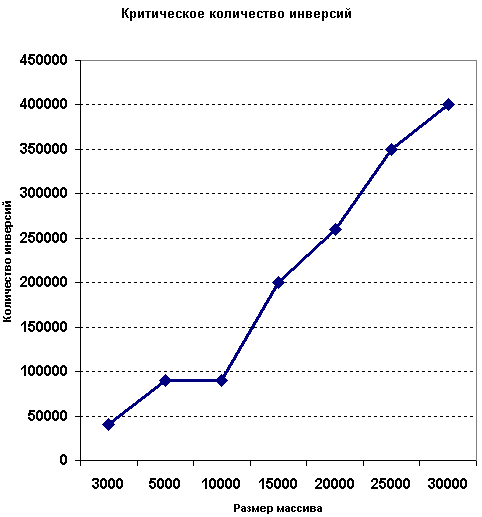
Легко видеть, что для массива размера n критическое количество инверсий составляет примерно 10*n. При большем количестве инверсий выгоден QuickSort. Следует отметить, что максимальное количество инверсий для массива длины n составляет n*(n-1)/2. Величина 10*n есть весьма незначительная их часть. Что и неудивительно.
К сказанному осталось добавить, что результаты таких экспериментов зависят от многих факторов (языка программирования, типа сортируемых данных и т.п.) Мне, честно говоря, было лень исследовать эти вопросы более детально. Мои эксперименты проводились в Microsoft Excel в среде VBA:
Спасибо за внимание!
PS
И спасибо всем, кто отметил мои ошибки! (Неверное написание Timsort — в первой редакции было «TeamSort» и пропущенное «i» в QuickSort), скорость-время в определении естественности. И — да! — (специально для перфекционистов) QuickSort может «деградировать» до квадратичной производительности. Но в заметке я рассматриваю не худший, а лучший случай применения QuickSort.
Ведь кроме показателя производительности есть и другие характеристики, зачастую — не менее важные. Один из них — естественность. Что это такое? Сортировка называется естественной, если она выполняется быстрее в том случае, когда массив уже почти отсортирован. А какой массив можно считать «почти отсортированным»? Вот два массива, состоящие из одних и тех элементов:
{1,2,9,3,4,5,7,6,8,10} и {9,1,6,3,10,5,4,2,8,7}
Даже на глаз видно, что первый массив более упорядочен (только 9 и 7 стоят «не на месте»). Тогда как во втором массиве числа перемешаны хаотически. Что же является мерой упорядоченности? Ответ известен — количество инверсий. Пара элементов A[i] и A[j] при j > i составляют инверсию, если A[j] < A[i]. (В этой заметке целью сортировки всегда является упорядочение по возрастанию).
Теперь можно дать точное определение: сортировка называется естественной, если время ее работы снижается при снижении количества инверсий в исходном массиве.
Естественность — достаточно «редкий фрукт» в мире сортировок — ни QuickSort ни сортировка Шелла не обладают этим свойством, увы. Но есть один алгоритм, который, можно сказать, является абсолютно естественным — это сортировка вставками. Хотя этот алгоритм известен каждому культурному человеку, позволю себе кратко повторить его суть.
Сортируемый массив просматривается один раз от начала к концу. Как только обнаруживается, что i-й и (i-1)-элементы образуют инверсию, i-й элемент «закидывается» назад (что достигается сдвигом нужного отрезка начала массива вправо на одну позицию). Из этого описания понятно, что если в массиве мало инверсий, алгоритм «пролетит» по массиву очень быстро. Если инверсий нет совсем, то алгоритм завершится за время O(n). А вот QuickSort в этом случае будет долго и утомительно выбирать разделяющий элемент, делить уже упорядоченный массив на отрезки и т.п. Но при наличии большого количества инверсий ситуация, разумеется, будет обратной: производительность сортировки вставками упадет до O(n^2), а QuickSort будет чемпионом — O(n*log(n)).
Сложившаяся ситуация порождает естественный с моей точки зрения вопрос: при каком количестве инверсий перевешивает естественность и сортировка вставками работает быстрее QuickSort?
Для ответа на этот вопрос я провел серию вычислительных экспериментов. Суть их состояла в следующем. Брались массивы целых чисел размером от 3000 до 30000 элементов, в них вносилось некоторое количество инверсий, затем массивы сортировались вставками и быстрой сортировкой. Замерялось время сортировки (в системных тиках). Для усреднения каждая сортировка повторялась 10 раз. Результаты оказались следующими:

На картинке представлены зависимости времени сортировки от количества внесенных инверсий. Малиновая серия — это, естественно, QuickSort, а синяя — сортировка вставками. Для размера массива 30 тыс. элементов, до примерно 400 тыс. инверсий «побеждает естественность». Для менее упорядоченных массивов уже выгоднее QuickSort.
А на следующей картинке приведена эмпирическая зависимость критического количества инверсий от размера массива.

Легко видеть, что для массива размера n критическое количество инверсий составляет примерно 10*n. При большем количестве инверсий выгоден QuickSort. Следует отметить, что максимальное количество инверсий для массива длины n составляет n*(n-1)/2. Величина 10*n есть весьма незначительная их часть. Что и неудивительно.
К сказанному осталось добавить, что результаты таких экспериментов зависят от многих факторов (языка программирования, типа сортируемых данных и т.п.) Мне, честно говоря, было лень исследовать эти вопросы более детально. Мои эксперименты проводились в Microsoft Excel в среде VBA:
Исходный код тестов
Private Declare Function GetTickCount Lib "kernel32" () As Long
'::: Сортировка вставками
Sub JSort(A() As Long)
n& = UBound(A, 1)
For i& = 2 To n
If A(i&) < A(i& - 1) Then
j& = i& - 1
x& = A(i&)
Do While (A(j&) > x&)
A(j& + 1) = A(j&)
j& = j& - 1
If j& = 0 Then Exit Do
Loop
A(j& + 1) = x&
End If
Next i&
End Sub
'::: Быстрая сортировка
Sub QSort(A() As Long, Optional b As Long = 1, Optional e As Long = 0)
If (e - b) <= 1 Then Exit Sub
i& = b
j& = e
w& = A((i& + j&) / 2)
Do While (i& < j&)
Do While (A(i&) < w&)
i& = i& + 1
Loop
Do While (A(j&) > w&)
j& = j& - 1
Loop
If i& < j& Then
tmp& = A(i&)
A(i&) = A(j&)
A(j&) = tmp&
i& = i& + 1
j& = j& - 1
End If
Loop
If j& > b Then QSort A, b, j&
If i& < e Then QSort A, i&, e
End Sub
'::: Случайные перестановки элементов (внесение инверсий)
Sub InsInv(A() As Long, k As Long)
n& = UBound(A, 1)
For i& = 1 To k
Do
k1& = n& * Rnd
k2& = n& * Rnd
If (k1& <> k2&) And (k1& >= 1) And (k2& >= 1) Then Exit Do
Loop
tmp& = A(k1&)
A(k1&) = A(k2&)
A(k2&) = tmp&
Next i&
End Sub
'::: Подсчет числа инверсий в массиве
Function NumInv(A() As Long) As Long
n& = UBound(A, 1)
For i& = 1 To n& - 1
For j& = i& + 1 To n&
If A(j&) < A(i&) Then NumInv = NumInv + 1
Next j&
Next i&
End Function
'::: Главный тест
Sub Gtest_1()
Dim Eta() As Long
Dim Arr() As Long
Size& = CLng(InputBox("Sz="))
ReDim Eta(1 To Size&) As Long
ReDim Arr(1 To Size&) As Long
Randomize
For i& = 1 To Size&
Eta(i&) = i&
Next i&
q# = Size& * (Size& - 1) / 2
For iii% = 1 To 10
InsInv Eta, CLng(iii%)
ni# = CDbl(NumInv(Eta))
Cells(iii%, 1).Value = ni#
DoEvents
S# = 0
For l% = 1 To 10
For i& = 1 To Size&
Arr(i&) = Eta(i&)
Next i&
TBeg& = GetTickCount
JSort Arr
TEnd& = GetTickCount
S# = S# + TEnd& - TBeg&
Next l%
Cells(iii%, 2).Value = S#
DoEvents
S# = 0
For l% = 1 To 10
For i& = 1 To Size&
Arr(i&) = Eta(i&)
Next i&
TBeg& = GetTickCount
QSort Arr, 1, Size&
TEnd& = GetTickCount
S# = S# + TEnd& - TBeg&
If Not check(Arr) Then Exit Sub
Next l%
Cells(iii%, 3).Value = S#
DoEvents
Next iii%
MsgBox "OK"
End Sub
Спасибо за внимание!
PS
И спасибо всем, кто отметил мои ошибки! (Неверное написание Timsort — в первой редакции было «TeamSort» и пропущенное «i» в QuickSort), скорость-время в определении естественности. И — да! — (специально для перфекционистов) QuickSort может «деградировать» до квадратичной производительности. Но в заметке я рассматриваю не худший, а лучший случай применения QuickSort.