Всем привет!
В этой статье я хочу рассказать про реализацию алгоритма сверхдлинного быстрого преобразования Фурье на ПЛИС. Написать эту статью меня побудило желание поделиться личным практическим опытом, который не хотелось бы потерять, оставив информацию только у себя в голове. А поскольку я больше не занимаюсь задачами цифровой обработки сигналов на ПЛИС, то я просто обязан передать доступные мне знания.
В этой статье показана невозможность реализации «классической» схемы очень длинного БПФ даже на самых современных кристаллах ПЛИС и предложен алгоритм, позволяющий это сделать. Также пошагово рассмотрена основная идея алгоритма: от математической составляющей до создания законченного решения на базе ПЛИС с использованием внешней DDR-памяти. Статья затронет тонкости проектирования многоканальных систем обработки для подобного класса задач и, в частности, опишет мой практический опыт.
Представьте, что вам необходимо разработать широкополосный спектроанализатор с высокой разрешающей способностью по частоте. Известно, что чем больше длина БПФ, тем выше разрешающая способность. То есть вам необходимо спроектировать систему, которая принимает сигналы от АЦП, делает некую обработку внутри FPGA и выдает данные по высокоскоростному интерфейсу (например, PCIe, USB etc.) на следующие стадии обработки данных.
Формализуем требования задания:
Приступим…
Прежде чем переходить к описанию алгоритма сверхдлинного преобразования Фурье, следует сказать о принципиальной невозможности реализации на ПЛИС классических схем БПФ при определенных длинах. Именно из-за этого возникает решение, которое будет описано в этой статье.
Представим, что перед вами стоит задача разработать узел БПФ длиной от 256К до 64М отсчетов. В свободном доступе от лидирующих вендоров Xilinx & (ex. Altera) Intel нет доступных ядер с длиной БПФ, превышающей 64К точек. Причиной служит огромный расход блочной памяти (BRAM) кристалла ПЛИС при увеличении длины БПФ. Не спасает и появление URAM блоков в микросхемах от Xilinx. Даже если вы напишете свое супер-оптимальное решение по классической схеме алгоритма БПФ через конвейерное соединение узлов бабочек и кросс-коммутационных узлов, вы не сможете реализовать его на ПЛИС. Почему?
При увеличении длины БПФ в N раз, как минимум во столько же раз пропорционально изменяется объем занимаемых ресурсов BRAM. Для БПФ в формате с плавающей точкой число узлов BRAM увеличивается пропорционально, но для БПФ в формате с фиксированной точкой оценка потребляемых ресурсов еще пессимистичнее. Это вызвано тем, что на каждой стадии вычисления БПФ (после каждой бабочки) разрядность промежуточных данных растет на 1 бит.
Конечная разрядность на выходе узла БПФ вычисляется по формуле
Для примера, БПФ длиной 1М отсчетов прибавляет ко входному сигналу 20 бит. Если входной сигнал имеет разрядность 16 бит, то выходной сигнал будет 36 бит соответственно.

Посмотрим на таблицу занимаемых ресурсов для БПФ 64К отсчетов на примере Xilinx. По грубой оценке, если вам нужно сделать блок Floating-Point FFT на 1М точек, то вам потребуется 400 * 16 = 6400 элементов блочной памяти типа RAMB36K или ~ 220 Мбит! Такими ресурсами обладает только топовый Virtex UltraScale+ (VU29P) и то за счет URAM ячеек.

На следующих таблицах показано, сколько внутренней памяти есть у современных FPGA от Xilinx на примере серии Kintex.
Kintex Ultrascale

Kintex Ultrascale+
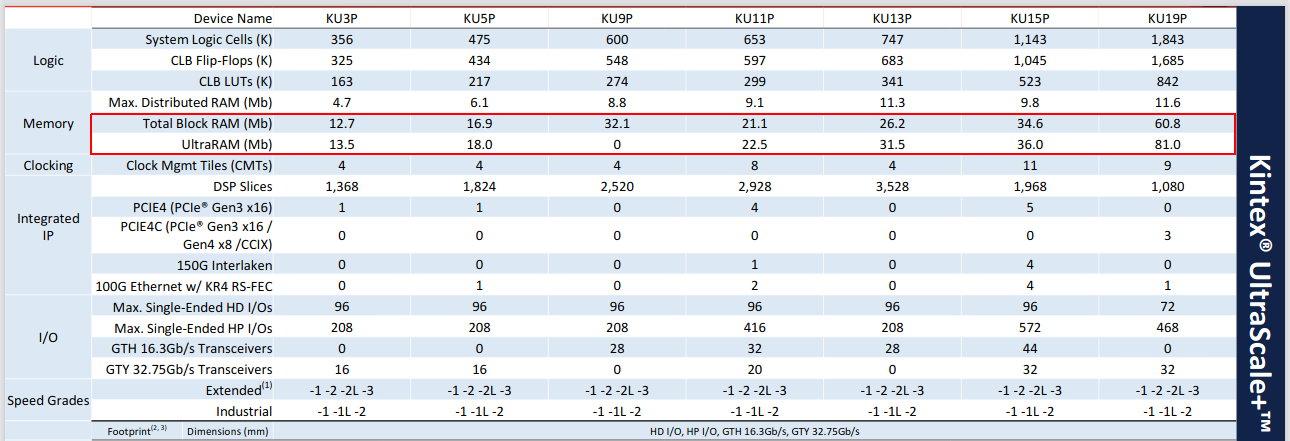
Как видно, ресурсы ПЛИС по блочной памяти сильно ограничены, поэтому реализовать БПФ даже для длины 1М точек в классическом виде практически невозможно.
К счастью, можно использовать небольшой математический трюк и сделать одномерное БПФ на базе двумерного.
Общая идея алгоритма в том, что вектор сигнала длины N разбивается на N1 и N2 отсчетов (где N1 и N2 кратны степени двойки). Этот вектор преобразуется в матрицу размерности N1 x N2, над которой производятся все вычисления. Короткие БПФ длиной N1 и N2 применяются к строкам и столбцам.
Формула для вычисления БПФ:
Разобъем последовательность N на произведение N1 и N2, тогда:
Тогда формула принимает вид:
После преобразования поворачивающих множителей:
Результат:
Можно заметить, что одномерное БПФ длины N превращается в два БПФ с длинами N1 и N2, и домножение результата первого БПФ на поворачивающие множители.
Структурная схема алгоритма сверхдлинного БПФ:
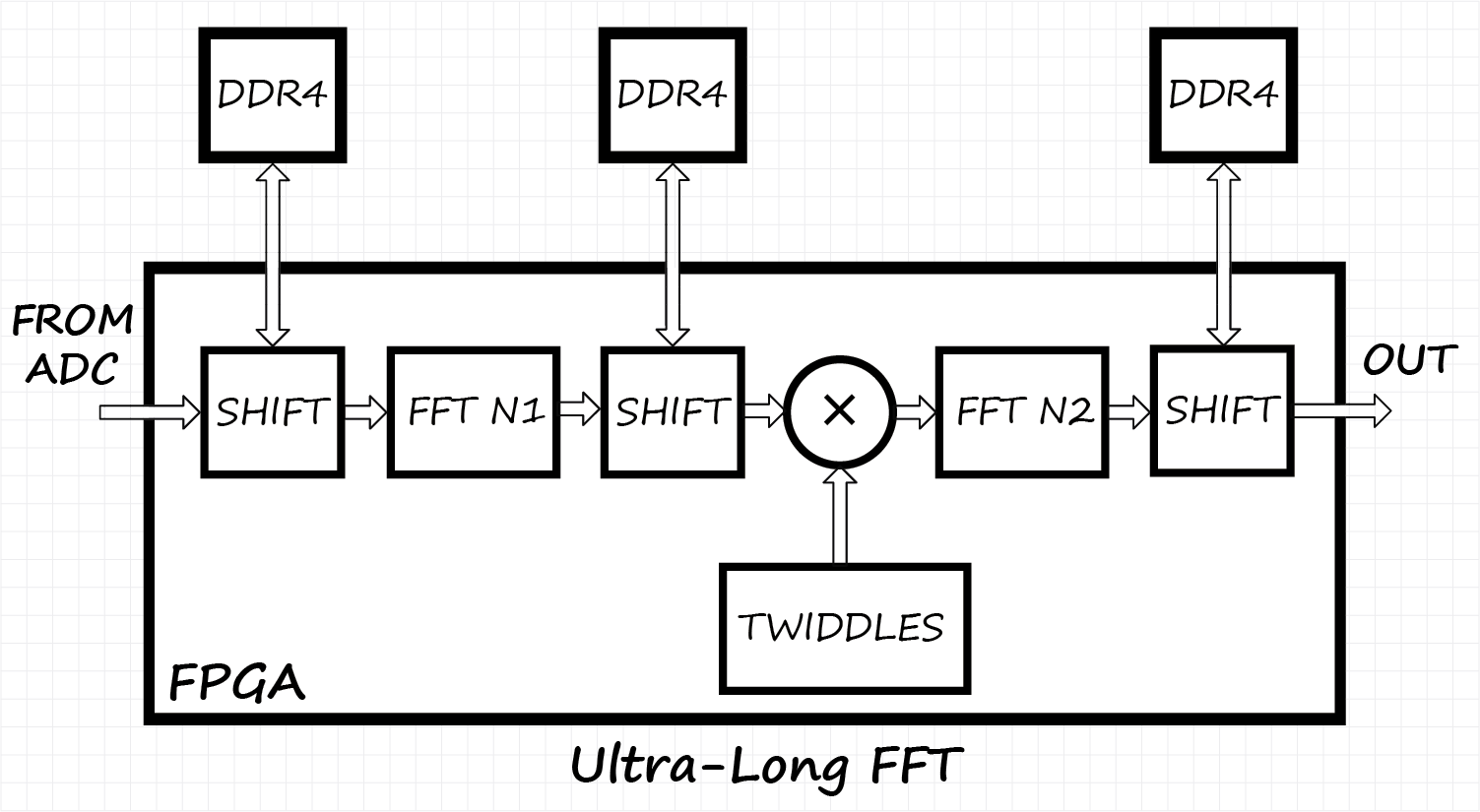
Стадии алгоритма:
Таким образом, используя три узла транспонирования данных и два блока БПФ небольшой длины, можно реализовать вычисление длинного БПФ.
Пример: ядро БПФ длиной 1М отсчетов. Можно разбить вычисление на два БПФ по 1К отсчетов: 1024 х 1024 = 1048576. На следующем рисунке показано, что узлу БПФ на 1024 точек требуется всего 7 ячеек RAMB36K.

Видно, что небольшие ядра БПФ практически не занимают ресурсы ПЛИС, в частности почти не используют блочную память. Пройдемся по всем элементам алгоритма и посмотрим на основные особенности каждого.
Узлы БПФ реализуются по классической конвейерной схеме — последовательное соединение log2(N) бабочек Radix-2 / Radix-4 и узлов кросс-коммутации. Можно использовать готовые бесплатные ядра от вендоров FPGA, либо написать свое оптимизированное ядро. Узлы FFT могут производить вычисления в формате fixed-point, floating-point или в каком-то своем кастомном формате, в зависимости от задачи.
Узел БПФ:
Необходимо понимать, что БПФ — это интегральный алгоритм, то есть на выходе БПФ растет разрядность данных (равно как и копится ошибка округления). Возникает вопрос: устраивает ли вас точность вычислений выбранного формата данных или нет? На моей практике, для сверхдлинных БПФ от длин 1М, ошибки округления операций floating-point (IEEE 754) портили результирующий спектр из-за небольшой мантиссы (25 бит). Поэтому приходилось использовать БПФ в fixed-point формате на всех стадиях обработки. В частном случае можно написать свою кастомную floating-point математику на DSP48 блоках ПЛИС с расширенной мантиссой (результат того стоит).
Ядро БПФ может быть реализовано с выдачей результата в бит-реверсном порядке, либо в натуральном (нормальном) порядке. В первом случае вы еще больше экономите ресурсы блочной памяти, но немного усложняете алгоритмы перестановок данных при транспонировании матриц. Если вы только начали реализовывать сверхдлинные БПФ, то начните со второго варианта, т.к. он проще в отладке.
Если вы реализуете многоканальную систему, а ядро БПФ написали сами, не используя готовое решение от производителей вашей ПЛИС, то можете дополнительно сэкономить память BRAM на хранении поворачивающих коэффициентов для бабочек БПФ. Для N независимых параллельных каналов можно использовать всего 1 модуль хранения поворачивающих множителей. То есть, чем больше канальность системы — тем больше экономия ресурсов.
Согласно схеме алгоритма, перед подачей матрицы на второе звено БПФ, данные необходимо домножить на поворачивающие множители. Сделать это можно двумя способами — использовать DDS или взять алгоритм CORDIC. Первый способ предполагает хранение большого массива данных, что требует значительного объема блочной памяти ПЛИС, за которую мы боремся с самого начала этой статьи. Теоретически, можно использовать аппроксимацию по Тейлору и сократить хранимый массив в BRAM. Но на моей практике такое решение искажает результирующий спектр из-за ступенчатой формы сигнала поворачивающих множителей.
Второй способ на базе CORDIC вообще не требует блочной памяти BRAM, так как использует итеративную схему применения операции сдвига и сложения/вычитания. К недостаткам алгоритма CORDIC можно отнести длительное время вычисления следующего значения (требуется порядка 20-30 тактов, число зависит от разрядности). Этот недостаток приводит к организации дополнительной линии задержки поступающих данных, что отнимает определенный логический ресурс ПЛИС. Например, для многоканальной схемы с разрядностью 512 (2 комплексных отсчета по 32 бит, 8 каналов) дополнительно потребуется 512 * 30 = 15 тысяч триггеров. В FPGA Xilinx для этого есть ячейки SLICEM, организующие линию задержки на сдвиговых регистрах. Либо на линию задержки можно потратить несколько блоков BRAM.
К ядру CORDIC выдвигаются следующие требования:
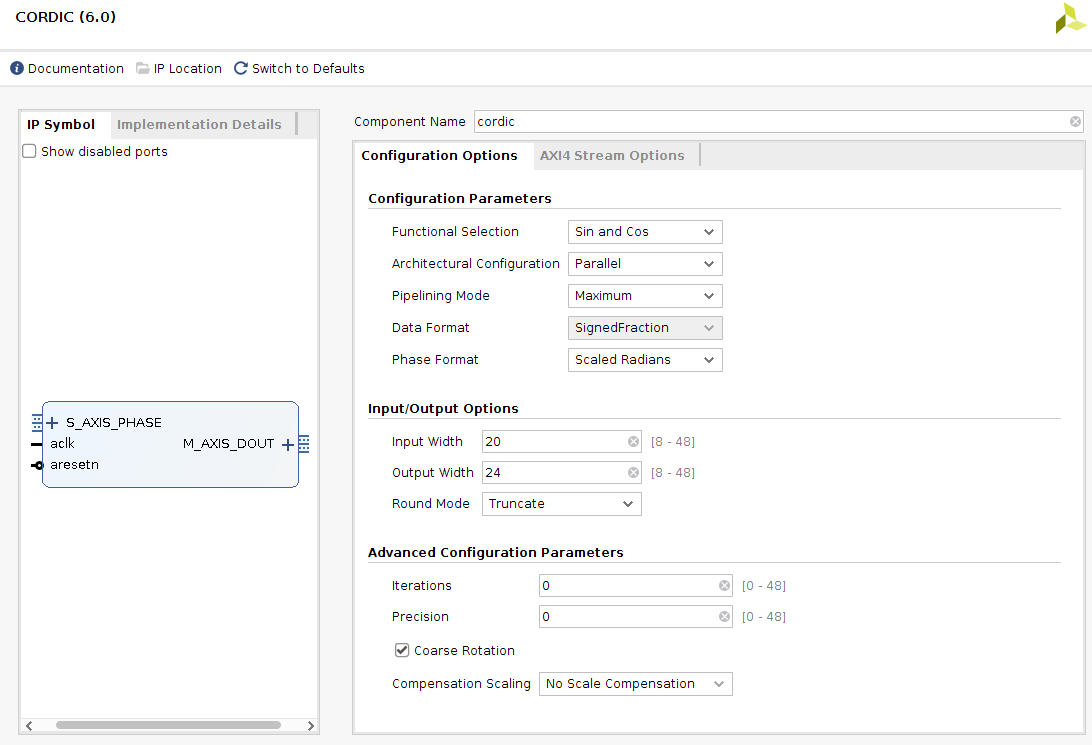
Для многоканальной схемы также можно использовать один узел поворачивающих множителей на весь поток данных и сэкономить ресурсы ПЛИС.
Контроллеры памяти используются для хранения векторов промежуточных данных, а также для транспонирования матрицы на всех стадиях алгоритма. Это может быть любая доступная вам память: QDR SRAM, DDR3 или DDR4 SDRAM. В своих проектах я использовал последние две. Но общие принципы работы одинаковы: контроллер памяти транспонирует выборку — получает пачку данных "по строкам", а выдает пачку данных в формате "по столбцам".
Как видно из схемы алгоритма, для этой задачи требуется три внешних узла памяти, к которым выделяются два главных требования.
Первое:
Память должна хранить минимальную выборку из 2 длин БПФ. Это необходимо для того, чтобы в процессе записи одной пачки данных в прямой форме (по строкам матрицы) иметь возможность успевать дочитать вторую пачку в инверсной форме (по столбцам матрицы). Но самое лучшее решение хранения данных не через мультиплексор, а когда внешняя память реализована по схеме FIFO. В таком случае внешняя память может хранить много пачек данных длиной N и эффективно использовать свой ресурс.
Также на практике такая схема позволяет бороться с небольшими замираниями интерфейса на выходе узла БПФ. В частности, при кратковременном замирании передачи по шине PCIe, вероятность переполнения памяти в режиме FIFO существенно ниже, чем у схемы с переключением между одной пачкой и другой. В реализованных мной проектах, DDR-память при замираниях на шине PCIe в режиме мультиплексора переполнялась почти всегда, а в режиме FIFO — никогда.
Рассчитаем объем для хранения данных во внешней памяти. Пусть разрядность входных данных 32 бита (single floating-point), сигнал — комплексный (I / Q), длина БПФ равна 1М отсчетов, схема реализации — "пинг-понг" как минимально необходимое требование. Тогда для хранения потребуется 2 * 32 / 8 = 8 МБ памяти. Для хранения данных в режиме FIFO глубиной 32 потребуется уже 256 МБ памяти.
Второе:
Память должна успевать записывать и читать данные в режиме реального времени. Согласно алгоритму, схема передачи данных на входе и выходе контроллера отличается. Поэтому нужно правильно организовать процесс передачи данных на максимальной скорости, чтобы не происходило разрывов и искажения данных. Для этого еще на этапе проектирования или покупки готовой платы, на которой будет работать сверхдлинное БПФ, нужно рассчитать максимальную пропускную способность всей системы. То есть найти максимальный поток ввода-вывода во внешнюю память согласно даташиту и определить скорость подачи данных от многоканального АЦП.
От длины БПФ пропускная способность не зависит.
Кроме того, к кристаллу ПЛИС предъявляется требование взаимодействия с тремя контроллерами памяти. Например, на каждый контроллер памяти SO-DIMM DDR4 SDRAM x64 необходимо три банка ПЛИС (эквивалентно ~150 физическим ножкам ввода-вывода кристалла). Суммарно потребуется не менее 450 I/O портов или 9 HP (High-Performance) банков ПЛИС, не считая банков мультигигабитных трансиверов и конфигурационного банка Bank0.
Пример настроек IP-ядра DDR4 SDRAM:

Алгоритм взаимодействия с контроллером памяти:
Итоговая схема взаимодействия с внешней памятью в режиме FIFO выглядит следующим образом:

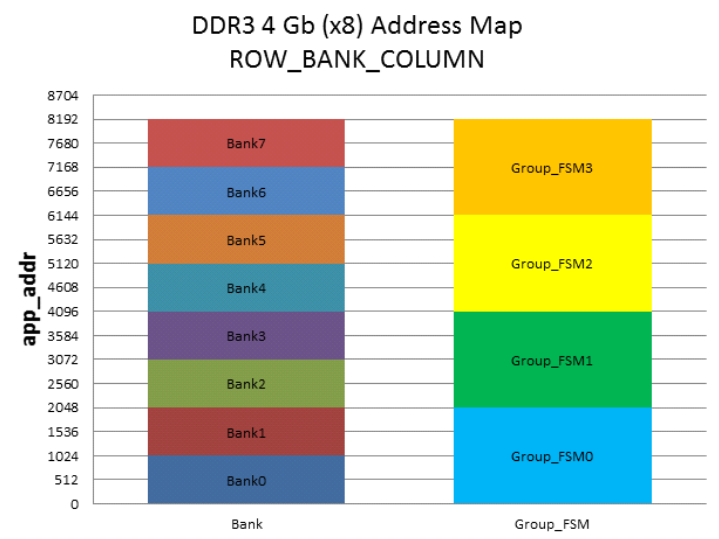
Следует отметить, что для достижения максимальной производительности, при чтении требуется производит обход по всем FSM группам контроллера памяти в ПЛИС (см. даташит на Xilinx DDR MIG), то есть нужно проходить по всем банкам и группам банков физической памяти. Это накладывает дополнительные ограничения и приводит к необходимости иметь буфер данных после контроллера памяти в ПЛИС. Его назначение — организация и упаковка обработанных транзакций с каждого банка памяти для дальнейшей передачи на следующие узлы схемы. Для реализации буфера данных идеально подходят модули URAM (блоки глубиной 4K и разрядностью 72 бит), которые появились в современных FPGA от Xilinx.
Также отмечу, что последний узел транспонирования можно использовать как аккумулятор, реализуя схему накопления спектральных компонент для усреднения результирующего спектра.
Наложение окна на входной сигнал — необязательная операция, но если вам необходимо добавить оконную функцию к длинному БПФ, то вы можете столкнуться с трудностями.
Поскольку мы используем сверхдлинные БПФ, то нам совсем негде хранить массив для оконных функций. Для БПФ длины N потребуется немало ресурсов блочной памяти. Например, оконная функция в виде 32-битного сигнала длиной 16М отсчетов потребует с учетом её симметричности: 32 * 4 / 2 = 256 Мбит. Даже для топовых кристаллов FPGA это много. А если нужно иметь возможность непрерывно переключать функции (как минимум потребуется два независимых буфера данных)?
Решить эту проблему можно очень просто, используя окна Блэкмана-Харриса нужного порядка и стандартную формулу вычисления коэффициентов окна. Применяя известный CORDIC для генерации гармонических сигналов нужной частоты, можно реализовать оконную функцию Блэкмана-Харриса любого порядка без использования блочной памяти FPGA!

Чем выше порядок оконной функции — тем ниже уровень боковых лепестков спектра. На практике мне приходилось использовать окна до 5 порядка. Останавливаться на этом не будем, более подробно об оконной фильтрации на ПЛИС я уже рассказывал в своей предыдущей статье.
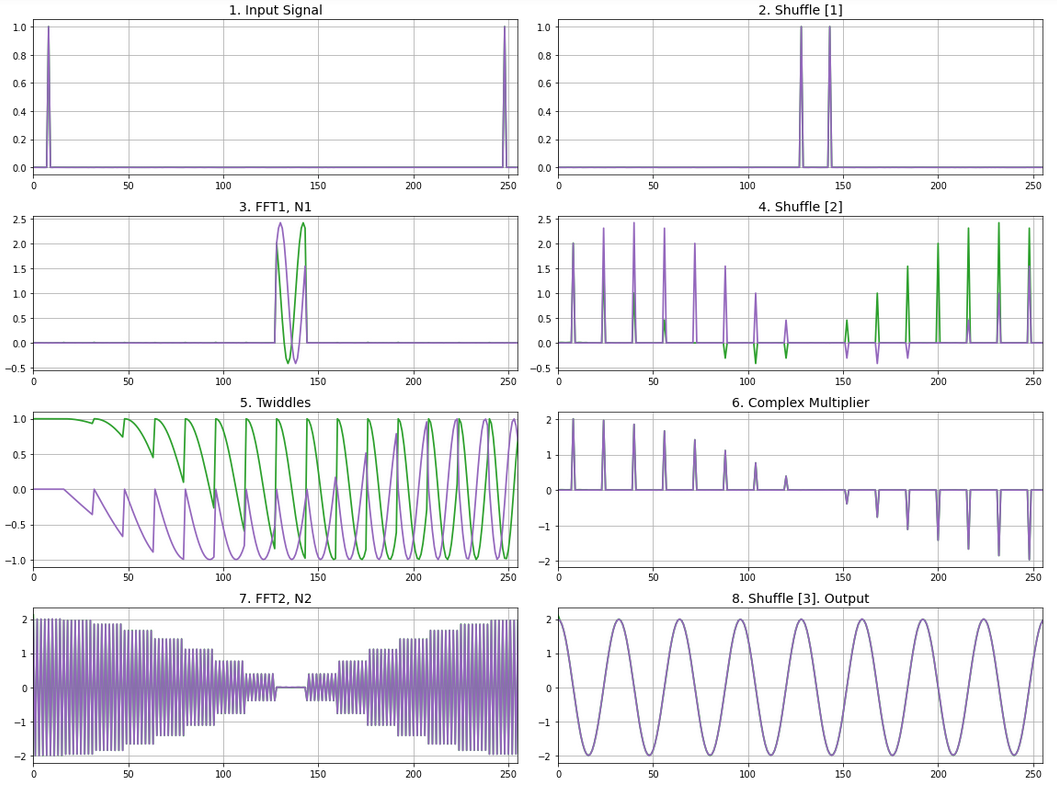
Ниже показано прохождение сигнала через узлы алгоритма сверхдлинного БПФ. В качестве входного воздействия выбран сигнал в виде пика на одном значении и ЛЧМ сигнал.
«Дельта-функция»:
ЛЧМ-сигнал:

Скрипт, который формирует данные на каждой стадии Ultra-Long FFT. Написан на Python, для его работы требуются библиотеки numpy, scipy и matplotlib.
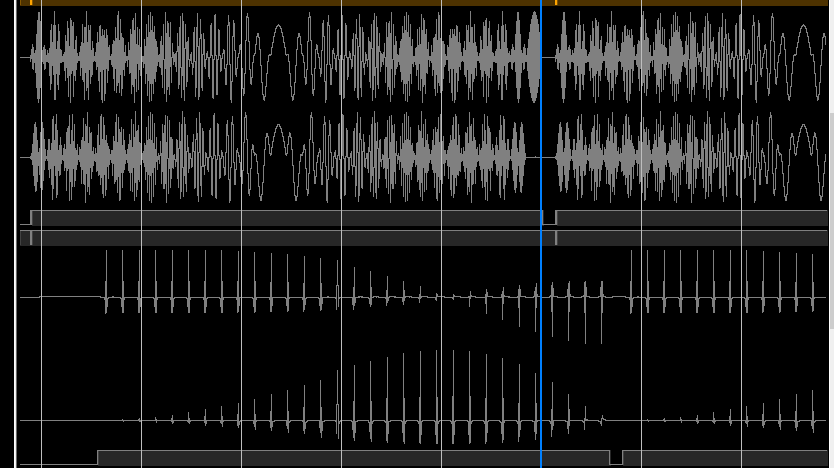
Транспонированный ЛЧМ сигнал до и после одной из стадий БПФ:
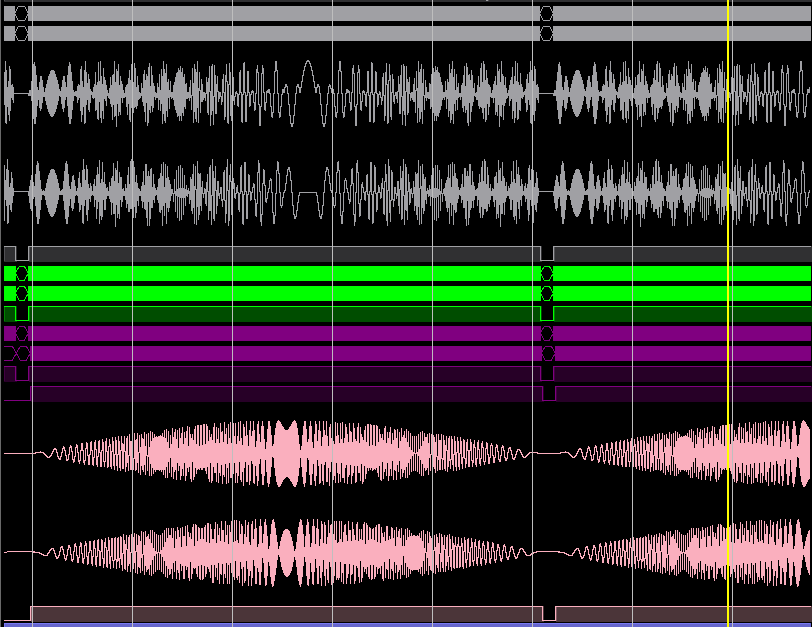
Прохождение ЛЧМ сигнала через узел БПФ:
Пусть перед вами стоит задача с такими вводными:
Расчёт:
Входной поток информации: (2 * 16) * 400e6 / 2^30 = ~1.5 ГБ/c.
Промежуточный поток информации: ~3 ГБ/c.
Объем памяти для хранения одной пачки БПФ: (2 * 32 / 8) * 16M = 128 МБ.
Пропускная способности памяти на чтение и запись — не менее ~6 ГБ/c.
Этому требованию удовлетворяет DDR4-2400 SDRAM x32 по формуле: Freq * Double Rate * (Width / Byte) = 1.2e9 * 2 * (32 / 8) / 2^30 = 8.94 ГБ/c.
С помощью IP Catalog создадим ядра DDR, FFT, CORDIC. Полное БПФ 16М точек раскладывается на матрицу БПФ как 4К х 4К. Пусть на перепаковку данных до и после контроллера DDR требуется FIFO, которые занимают 4 ячейки блочной памяти RAMB36K.
Грубая оценка потребления ресурсов ПЛИС на реализацию алгоритма. Нам необходимо 3 контроллера памяти, 2 узла БПФ 4К, один CORDIC, 6 блоков FIFO (до и после контроллеров памяти), 3 буфера банков памяти. Для простоты не будем учитывать линии задержки для согласования потока, комплексные умножители и остальную логику.
Результирующая таблица:
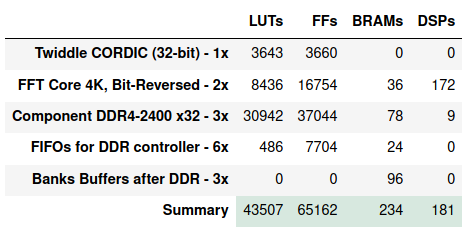
Как видно, проект занимает не очень много ресурсов и помещается в относительно дешевые ПЛИС. Однако, не стоит забывать, что 3 контроллера памяти требуют определенное количество I/O портов ПЛИС, поэтому подойдут не все микросхемы.
В данной статье показан способ реализации узлов сверхдлинных БПФ на ПЛИС в задачах высокоточного анализа спектра сигнала в режиме реального времени. Проектирование такого алгоритма требует определенной конфигурации «хардварной» части — к ПЛИС должны подключаться три независимых контроллера памяти. Однако, это позволяет создавать схемы очень длинных БПФ с количеством точек от 256К до 256М. Поскольку алгоритм имеет много нюансов в аппаратной реализации, необходимо заранее просчитать параметры всех узлов схемы и убедиться в реализуемости ядра на выбранной вами конфигурации.
Для реализации алгоритма сверхдлинного БПФ идеально подходят платы Alveo U200 / U250 от Xilinx (4 контроллера DDR4 на борту) или Alveo U280 (два DIMM DDR4 и HBM2).
Спасибо за внимание!
В этой статье я хочу рассказать про реализацию алгоритма сверхдлинного быстрого преобразования Фурье на ПЛИС. Написать эту статью меня побудило желание поделиться личным практическим опытом, который не хотелось бы потерять, оставив информацию только у себя в голове. А поскольку я больше не занимаюсь задачами цифровой обработки сигналов на ПЛИС, то я просто обязан передать доступные мне знания.
В этой статье показана невозможность реализации «классической» схемы очень длинного БПФ даже на самых современных кристаллах ПЛИС и предложен алгоритм, позволяющий это сделать. Также пошагово рассмотрена основная идея алгоритма: от математической составляющей до создания законченного решения на базе ПЛИС с использованием внешней DDR-памяти. Статья затронет тонкости проектирования многоканальных систем обработки для подобного класса задач и, в частности, опишет мой практический опыт.

Постановка задачи
Представьте, что вам необходимо разработать широкополосный спектроанализатор с высокой разрешающей способностью по частоте. Известно, что чем больше длина БПФ, тем выше разрешающая способность. То есть вам необходимо спроектировать систему, которая принимает сигналы от АЦП, делает некую обработку внутри FPGA и выдает данные по высокоскоростному интерфейсу (например, PCIe, USB etc.) на следующие стадии обработки данных.
Формализуем требования задания:
- Алгоритм: быстрое преобразование Фурье
- Длина БПФ от 256K до 256M точек.
- Непрерывная обработка данных в реалтайме.
- Количество независимых каналов на входе — от 1 до N.
- Разрядность сигналов АЦП — от 16 бит.
- Комплексный сигнал на входе.
- Частота поступления данных от одного канала АЦП — от 200 МГЦ и выше.
- Наличие переключаемой оконной функции перед звеном БПФ.
Приступим…
Классический подход не работает!
Прежде чем переходить к описанию алгоритма сверхдлинного преобразования Фурье, следует сказать о принципиальной невозможности реализации на ПЛИС классических схем БПФ при определенных длинах. Именно из-за этого возникает решение, которое будет описано в этой статье.
Представим, что перед вами стоит задача разработать узел БПФ длиной от 256К до 64М отсчетов. В свободном доступе от лидирующих вендоров Xilinx & (ex. Altera) Intel нет доступных ядер с длиной БПФ, превышающей 64К точек. Причиной служит огромный расход блочной памяти (BRAM) кристалла ПЛИС при увеличении длины БПФ. Не спасает и появление URAM блоков в микросхемах от Xilinx. Даже если вы напишете свое супер-оптимальное решение по классической схеме алгоритма БПФ через конвейерное соединение узлов бабочек и кросс-коммутационных узлов, вы не сможете реализовать его на ПЛИС. Почему?
При увеличении длины БПФ в N раз, как минимум во столько же раз пропорционально изменяется объем занимаемых ресурсов BRAM. Для БПФ в формате с плавающей точкой число узлов BRAM увеличивается пропорционально, но для БПФ в формате с фиксированной точкой оценка потребляемых ресурсов еще пессимистичнее. Это вызвано тем, что на каждой стадии вычисления БПФ (после каждой бабочки) разрядность промежуточных данных растет на 1 бит.
Конечная разрядность на выходе узла БПФ вычисляется по формуле
Для примера, БПФ длиной 1М отсчетов прибавляет ко входному сигналу 20 бит. Если входной сигнал имеет разрядность 16 бит, то выходной сигнал будет 36 бит соответственно.

Посмотрим на таблицу занимаемых ресурсов для БПФ 64К отсчетов на примере Xilinx. По грубой оценке, если вам нужно сделать блок Floating-Point FFT на 1М точек, то вам потребуется 400 * 16 = 6400 элементов блочной памяти типа RAMB36K или ~ 220 Мбит! Такими ресурсами обладает только топовый Virtex UltraScale+ (VU29P) и то за счет URAM ячеек.

На следующих таблицах показано, сколько внутренней памяти есть у современных FPGA от Xilinx на примере серии Kintex.
Kintex Ultrascale

Kintex Ultrascale+

Как видно, ресурсы ПЛИС по блочной памяти сильно ограничены, поэтому реализовать БПФ даже для длины 1М точек в классическом виде практически невозможно.
Сверхдлинное БПФ
К счастью, можно использовать небольшой математический трюк и сделать одномерное БПФ на базе двумерного.
Общая идея алгоритма в том, что вектор сигнала длины N разбивается на N1 и N2 отсчетов (где N1 и N2 кратны степени двойки). Этот вектор преобразуется в матрицу размерности N1 x N2, над которой производятся все вычисления. Короткие БПФ длиной N1 и N2 применяются к строкам и столбцам.
Формула для вычисления БПФ:
Разобъем последовательность N на произведение N1 и N2, тогда:
Тогда формула принимает вид:
После преобразования поворачивающих множителей:
Результат:
Можно заметить, что одномерное БПФ длины N превращается в два БПФ с длинами N1 и N2, и домножение результата первого БПФ на поворачивающие множители.
Структурная схема алгоритма сверхдлинного БПФ:

Стадии алгоритма:
- Транспонирование одномерной последовательности в матрицу K1 x K2
- Вычисление БПФ по K1 строкам K2 раз
- Транспонирование полученной матрицы
- Умножение результатов на поворачивающие множители
- Вычисление БПФ по K2 столбцам K1 раз
- Транспонирование матрицы в исходный одномерный вектор
Таким образом, используя три узла транспонирования данных и два блока БПФ небольшой длины, можно реализовать вычисление длинного БПФ.
Пример: ядро БПФ длиной 1М отсчетов. Можно разбить вычисление на два БПФ по 1К отсчетов: 1024 х 1024 = 1048576. На следующем рисунке показано, что узлу БПФ на 1024 точек требуется всего 7 ячеек RAMB36K.

Видно, что небольшие ядра БПФ практически не занимают ресурсы ПЛИС, в частности почти не используют блочную память. Пройдемся по всем элементам алгоритма и посмотрим на основные особенности каждого.
Пошаговая реализация
Блоки БПФ
Узлы БПФ реализуются по классической конвейерной схеме — последовательное соединение log2(N) бабочек Radix-2 / Radix-4 и узлов кросс-коммутации. Можно использовать готовые бесплатные ядра от вендоров FPGA, либо написать свое оптимизированное ядро. Узлы FFT могут производить вычисления в формате fixed-point, floating-point или в каком-то своем кастомном формате, в зависимости от задачи.
Узел БПФ:
- Конвейерная параллельная схема (Pipelined, Streaming I/O)
- Fixed Unscaled / Floating point
- Radix-2 / Radix-4
- Bit-Reverse / Natural Order
- Complex multiplier: 4-DSP structure
Необходимо понимать, что БПФ — это интегральный алгоритм, то есть на выходе БПФ растет разрядность данных (равно как и копится ошибка округления). Возникает вопрос: устраивает ли вас точность вычислений выбранного формата данных или нет? На моей практике, для сверхдлинных БПФ от длин 1М, ошибки округления операций floating-point (IEEE 754) портили результирующий спектр из-за небольшой мантиссы (25 бит). Поэтому приходилось использовать БПФ в fixed-point формате на всех стадиях обработки. В частном случае можно написать свою кастомную floating-point математику на DSP48 блоках ПЛИС с расширенной мантиссой (результат того стоит).
Ядро БПФ может быть реализовано с выдачей результата в бит-реверсном порядке, либо в натуральном (нормальном) порядке. В первом случае вы еще больше экономите ресурсы блочной памяти, но немного усложняете алгоритмы перестановок данных при транспонировании матриц. Если вы только начали реализовывать сверхдлинные БПФ, то начните со второго варианта, т.к. он проще в отладке.
Если вы реализуете многоканальную систему, а ядро БПФ написали сами, не используя готовое решение от производителей вашей ПЛИС, то можете дополнительно сэкономить память BRAM на хранении поворачивающих коэффициентов для бабочек БПФ. Для N независимых параллельных каналов можно использовать всего 1 модуль хранения поворачивающих множителей. То есть, чем больше канальность системы — тем больше экономия ресурсов.
Поворачивающие множители
Согласно схеме алгоритма, перед подачей матрицы на второе звено БПФ, данные необходимо домножить на поворачивающие множители. Сделать это можно двумя способами — использовать DDS или взять алгоритм CORDIC. Первый способ предполагает хранение большого массива данных, что требует значительного объема блочной памяти ПЛИС, за которую мы боремся с самого начала этой статьи. Теоретически, можно использовать аппроксимацию по Тейлору и сократить хранимый массив в BRAM. Но на моей практике такое решение искажает результирующий спектр из-за ступенчатой формы сигнала поворачивающих множителей.
Второй способ на базе CORDIC вообще не требует блочной памяти BRAM, так как использует итеративную схему применения операции сдвига и сложения/вычитания. К недостаткам алгоритма CORDIC можно отнести длительное время вычисления следующего значения (требуется порядка 20-30 тактов, число зависит от разрядности). Этот недостаток приводит к организации дополнительной линии задержки поступающих данных, что отнимает определенный логический ресурс ПЛИС. Например, для многоканальной схемы с разрядностью 512 (2 комплексных отсчета по 32 бит, 8 каналов) дополнительно потребуется 512 * 30 = 15 тысяч триггеров. В FPGA Xilinx для этого есть ячейки SLICEM, организующие линию задержки на сдвиговых регистрах. Либо на линию задержки можно потратить несколько блоков BRAM.
К ядру CORDIC выдвигаются следующие требования:
- Параллельная схема обработки
- Разрядность входных данных не менее log2(N) от конечной длины БПФ для отсутствия искажений в спектре сигнала.

Для многоканальной схемы также можно использовать один узел поворачивающих множителей на весь поток данных и сэкономить ресурсы ПЛИС.
Узлы транспонирования
Контроллеры памяти используются для хранения векторов промежуточных данных, а также для транспонирования матрицы на всех стадиях алгоритма. Это может быть любая доступная вам память: QDR SRAM, DDR3 или DDR4 SDRAM. В своих проектах я использовал последние две. Но общие принципы работы одинаковы: контроллер памяти транспонирует выборку — получает пачку данных "по строкам", а выдает пачку данных в формате "по столбцам".
Как видно из схемы алгоритма, для этой задачи требуется три внешних узла памяти, к которым выделяются два главных требования.
Первое:
Память должна хранить минимальную выборку из 2 длин БПФ. Это необходимо для того, чтобы в процессе записи одной пачки данных в прямой форме (по строкам матрицы) иметь возможность успевать дочитать вторую пачку в инверсной форме (по столбцам матрицы). Но самое лучшее решение хранения данных не через мультиплексор, а когда внешняя память реализована по схеме FIFO. В таком случае внешняя память может хранить много пачек данных длиной N и эффективно использовать свой ресурс.
Также на практике такая схема позволяет бороться с небольшими замираниями интерфейса на выходе узла БПФ. В частности, при кратковременном замирании передачи по шине PCIe, вероятность переполнения памяти в режиме FIFO существенно ниже, чем у схемы с переключением между одной пачкой и другой. В реализованных мной проектах, DDR-память при замираниях на шине PCIe в режиме мультиплексора переполнялась почти всегда, а в режиме FIFO — никогда.
Рассчитаем объем для хранения данных во внешней памяти. Пусть разрядность входных данных 32 бита (single floating-point), сигнал — комплексный (I / Q), длина БПФ равна 1М отсчетов, схема реализации — "пинг-понг" как минимально необходимое требование. Тогда для хранения потребуется 2 * 32 / 8 = 8 МБ памяти. Для хранения данных в режиме FIFO глубиной 32 потребуется уже 256 МБ памяти.
Второе:
Память должна успевать записывать и читать данные в режиме реального времени. Согласно алгоритму, схема передачи данных на входе и выходе контроллера отличается. Поэтому нужно правильно организовать процесс передачи данных на максимальной скорости, чтобы не происходило разрывов и искажения данных. Для этого еще на этапе проектирования или покупки готовой платы, на которой будет работать сверхдлинное БПФ, нужно рассчитать максимальную пропускную способность всей системы. То есть найти максимальный поток ввода-вывода во внешнюю память согласно даташиту и определить скорость подачи данных от многоканального АЦП.
От длины БПФ пропускная способность не зависит.
Кроме того, к кристаллу ПЛИС предъявляется требование взаимодействия с тремя контроллерами памяти. Например, на каждый контроллер памяти SO-DIMM DDR4 SDRAM x64 необходимо три банка ПЛИС (эквивалентно ~150 физическим ножкам ввода-вывода кристалла). Суммарно потребуется не менее 450 I/O портов или 9 HP (High-Performance) банков ПЛИС, не считая банков мультигигабитных трансиверов и конфигурационного банка Bank0.
Пример настроек IP-ядра DDR4 SDRAM:

Алгоритм взаимодействия с контроллером памяти:
- входной поток поступает на небольшое FIFO на частоте обработки и преобразуется в поток на частоте контроллера памяти (например, 333 МГц)
- данные записываются в память в прямой форме, с линейным увеличением счетчика адреса памяти DDR.
- после записи пачки размером N = K1 * K2 происходит чтение в инверсной форме.
- счетчик адреса памяти DDR на чтение меняется по определенному алгоритму с заданным шагом, чтобы обеспечить транспонирование матрицы K1 x K2.
- одновременно с чтением продолжается запись в другую, свободную область внешней памяти.
- прочитанный поток данных преобразуется с частоты контроллера на частоту обработки (с помощью небольшого FIFO).
- если на стороне чтения по каким-то причинам происходит остановка (замирание), запись не прекращается и продолжается до тех пор, пока контроллер не установит флаг FULL FIFO.
Итоговая схема взаимодействия с внешней памятью в режиме FIFO выглядит следующим образом:

Следует отметить, что для достижения максимальной производительности, при чтении требуется производит обход по всем FSM группам контроллера памяти в ПЛИС (см. даташит на Xilinx DDR MIG), то есть нужно проходить по всем банкам и группам банков физической памяти. Это накладывает дополнительные ограничения и приводит к необходимости иметь буфер данных после контроллера памяти в ПЛИС. Его назначение — организация и упаковка обработанных транзакций с каждого банка памяти для дальнейшей передачи на следующие узлы схемы. Для реализации буфера данных идеально подходят модули URAM (блоки глубиной 4K и разрядностью 72 бит), которые появились в современных FPGA от Xilinx.

Также отмечу, что последний узел транспонирования можно использовать как аккумулятор, реализуя схему накопления спектральных компонент для усреднения результирующего спектра.
Оконная функция
Наложение окна на входной сигнал — необязательная операция, но если вам необходимо добавить оконную функцию к длинному БПФ, то вы можете столкнуться с трудностями.
Поскольку мы используем сверхдлинные БПФ, то нам совсем негде хранить массив для оконных функций. Для БПФ длины N потребуется немало ресурсов блочной памяти. Например, оконная функция в виде 32-битного сигнала длиной 16М отсчетов потребует с учетом её симметричности: 32 * 4 / 2 = 256 Мбит. Даже для топовых кристаллов FPGA это много. А если нужно иметь возможность непрерывно переключать функции (как минимум потребуется два независимых буфера данных)?
Решить эту проблему можно очень просто, используя окна Блэкмана-Харриса нужного порядка и стандартную формулу вычисления коэффициентов окна. Применяя известный CORDIC для генерации гармонических сигналов нужной частоты, можно реализовать оконную функцию Блэкмана-Харриса любого порядка без использования блочной памяти FPGA!

Чем выше порядок оконной функции — тем ниже уровень боковых лепестков спектра. На практике мне приходилось использовать окна до 5 порядка. Останавливаться на этом не будем, более подробно об оконной фильтрации на ПЛИС я уже рассказывал в своей предыдущей статье.
Контрольные точки
Ниже показано прохождение сигнала через узлы алгоритма сверхдлинного БПФ. В качестве входного воздействия выбран сигнал в виде пика на одном значении и ЛЧМ сигнал.
«Дельта-функция»:

ЛЧМ-сигнал:

Скрипт, который формирует данные на каждой стадии Ultra-Long FFT. Написан на Python, для его работы требуются библиотеки numpy, scipy и matplotlib.
Python-код для картинок
from datetime import datetime
from functools import lru_cache
import matplotlib.pyplot as plt
import numpy as np
from scipy.fftpack import fft
N1 = 8 # Colomn (FFT1)
N2 = 16 # Rows (FFT2)
class SignalGenerator:
def __init__(
self, nfft: int, freq: float, alpha: float = 0.01,
):
"""Generate some useful kind of signals: harmonic or linear freq. modulated.
Parameters
----------
nfft : int
Total lenght of FFT (NFFT = N1 * N2).
freq : float
Signal frequency.
alpha : float
Add Gaussian noise if alpha not equal to zero. Should be positive.
"""
self.nfft = nfft
self.freq = freq
self.alpha = alpha
def awgn(self):
np.random.seed(42)
return self.alpha * np.random.rand(self.nfft)
def input_harmonic(self):
"""Generate input singal"""
return (
np.array([1 + 1j if i in (self.freq, self.nfft - self.freq) else 0 for i in range(self.nfft)]) + self.awgn()
)
def input_linfreq(self):
tt = np.linspace(0, 1, self.nfft, endpoint=False)
sig_re = np.cos(self.freq * tt ** 2 * np.pi) * np.sin(tt * np.pi) + self.awgn()
sig_im = np.sin(self.freq * tt ** 2 * np.pi) * np.sin(tt * np.pi) + self.awgn()
return sig_re + 1j * sig_im
class UltraLongFFT:
"""Calculate ultra-long FFT via 2D FFT scheme with 3 shufflers: step by step.
Parameters
----------
n1 : int
Rows (number of points for 1st FFTs)
n2 : int
Columns (number of points for 2ns FFTs)
where NFFT = N1 * N2
"""
_plt_titles = (
"1. Input Signal",
"2. Shuffle [1]",
"3. FFT1, N1",
"4. Shuffle [2]",
"5. Twiddles",
"6. Complex Multiplier",
"7. FFT2, N2",
"8. Shuffle [3]. Output",
)
def __init__(self, n1: int = 32, n2: int = 32):
self.n1 = n1
self.n2 = n2
self.__nfft = n1 * n2
@property
@lru_cache(maxsize=4)
def twiddles(self):
"""Twiddle factors for rotating internal sequence."""
twd = np.array(
[np.exp(-1j * 2 * np.pi * (k1 * k2) / self.__nfft) for k1 in range(self.n1) for k2 in range(self.n2)]
)
return np.reshape(twd, (self.n1, self.n2))
def fft_calculate(self, signal: np.ndarray) -> np.ndarray:
"""Calculate signals for each stage of Ultra-long FFT Algorithm
Parameters
----------
signal : np.ndarray
Input signal. Can be complex.
Returns
-------
np.ndarray
List of arrays for each stage of Ultra-long FFT.
"""
# ---------------- ULFFT Algorithm ----------------
# 1 Step: Shuffle input sequence
sh0_data = np.reshape(
a=np.array([signal[k2 * self.n1 + k1] for k1 in range(self.n1) for k2 in range(self.n2)]),
newshape=(self.n1, self.n2),
)
# 2 Step: Calculate FFT N1 and shuffle
res_fft0 = np.array([fft(sh0_data[k1, ...]) for k1 in range(self.n1)])
# 3 Step: Complex multiplier
cmp_data = res_fft0 * self.twiddles
# 4 Step: Calculate FFT N2 and shuffle
res_fft1 = np.array([fft(cmp_data[..., k2]) for k2 in range(self.n2)])
# Internal Sequences:
return np.vstack(
[
signal,
sh0_data.reshape(-1, self.__nfft),
res_fft0.reshape(-1, self.__nfft),
res_fft0.T.reshape(-1, self.__nfft),
self.twiddles.reshape(-1, self.__nfft),
cmp_data.T.reshape(-1, self.__nfft),
res_fft1.reshape(-1, self.__nfft),
res_fft1.T.reshape(-1, self.__nfft),
]
)
def plot_result(self, data: np.ndarray, save_fig: bool = False):
"""Plot signals for each stage of Ultra-long FFT Algorithm"""
_ = plt.figure("Ultra-long FFT", figsize=(16, 12))
for i, arr in enumerate(data):
plt.subplot(4, 2, i + 1)
plt.plot(arr.real, linewidth=1.15, color="C2")
plt.plot(arr.imag, linewidth=1.15, color="C4")
plt.title(self._plt_titles[i], fontsize=14)
plt.grid(True)
plt.xlim([0, self.__nfft - 1])
plt.tight_layout()
if save_fig:
plt.savefig(f"figure_{datetime.now()}"[:-7])
plt.show()
if __name__ == "__main__":
_input = SignalGenerator(N1 * N2, freq=16, alpha=0.001)
# _array = _input.input_harmonic()
_array = _input.input_linfreq()
_ulfft = UltraLongFFT(N1, N2)
_datas = _ulfft.fft_calculate(_array)
_ulfft.plot_result(_datas, save_fig=False)
Диаграммы в Vivado
Транспонированный ЛЧМ сигнал до и после одной из стадий БПФ:

Прохождение ЛЧМ сигнала через узел БПФ:

Практический пример
Пусть перед вами стоит задача с такими вводными:
- Входной сигнал — комплексный, разрядность 16 бит.
- Число каналов — 1. Частота дискретизации 400 МГц.
- Промежуточные данные в формате IEEE-754.
- Длина БПФ: 16 миллионов точек. Без оконной функции.
Расчёт:
Входной поток информации: (2 * 16) * 400e6 / 2^30 = ~1.5 ГБ/c.
Промежуточный поток информации: ~3 ГБ/c.
Объем памяти для хранения одной пачки БПФ: (2 * 32 / 8) * 16M = 128 МБ.
Пропускная способности памяти на чтение и запись — не менее ~6 ГБ/c.
Этому требованию удовлетворяет DDR4-2400 SDRAM x32 по формуле: Freq * Double Rate * (Width / Byte) = 1.2e9 * 2 * (32 / 8) / 2^30 = 8.94 ГБ/c.
С помощью IP Catalog создадим ядра DDR, FFT, CORDIC. Полное БПФ 16М точек раскладывается на матрицу БПФ как 4К х 4К. Пусть на перепаковку данных до и после контроллера DDR требуется FIFO, которые занимают 4 ячейки блочной памяти RAMB36K.
Грубая оценка потребления ресурсов ПЛИС на реализацию алгоритма. Нам необходимо 3 контроллера памяти, 2 узла БПФ 4К, один CORDIC, 6 блоков FIFO (до и после контроллеров памяти), 3 буфера банков памяти. Для простоты не будем учитывать линии задержки для согласования потока, комплексные умножители и остальную логику.
Результирующая таблица:

Как видно, проект занимает не очень много ресурсов и помещается в относительно дешевые ПЛИС. Однако, не стоит забывать, что 3 контроллера памяти требуют определенное количество I/O портов ПЛИС, поэтому подойдут не все микросхемы.
Заключение
В данной статье показан способ реализации узлов сверхдлинных БПФ на ПЛИС в задачах высокоточного анализа спектра сигнала в режиме реального времени. Проектирование такого алгоритма требует определенной конфигурации «хардварной» части — к ПЛИС должны подключаться три независимых контроллера памяти. Однако, это позволяет создавать схемы очень длинных БПФ с количеством точек от 256К до 256М. Поскольку алгоритм имеет много нюансов в аппаратной реализации, необходимо заранее просчитать параметры всех узлов схемы и убедиться в реализуемости ядра на выбранной вами конфигурации.
Для реализации алгоритма сверхдлинного БПФ идеально подходят платы Alveo U200 / U250 от Xilinx (4 контроллера DDR4 на борту) или Alveo U280 (два DIMM DDR4 и HBM2).
Список литературы
- Авторский курс лекций по цифровой обработке сигналов
- Особенности оконной фильтрации на ПЛИС
- Айфичер Э., Джервис Б. Цифровая обработка сигналов. Практический подход
- Рабинер и Голд. Теория и практика цифровой обработки сигналов
- Xilinx PG109: Fast Fourier Transform
- Xilinx PG105: CORDIC
- Xilinx PG150: MIG Ultrascale
- Ultra-long FFT IP core for Xilinx FPGAs
- An Ultra-long FFT Architecture
Спасибо за внимание!