На волне ажиотажа вокруг новых карточек от Nvidia с поддержкой RTX, я, сканируя хабр в поисках интересных статей, с удивлением обнаружил, что такая тема, как трассировка путей, здесь практически не освещена. "Так дело не пойдет" - подумал я и решил, что неплохо бы сделать что-нибудь небольшое на эту тему, да и так, чтоб другим полезно было. Тут как кстати API собственного движка нужно было протестировать, поэтому решил: запилю-ка я свой простенький path-tracer. Что же из этого вышло вы думаю уже догадались по превью к данной статье.

Немного теории
Трассировка пути является одним из частных случаев трассировки лучей и представляет собой наиболее точный с физической точки зрения способ рендеринга. Используя непосредственное моделирование распространения света для расчета освещения, этот алгоритм позволяет с минимальными усилиями получать весьма реалистичные сцены, для рендеринга которых традиционным способом ушло бы неимоверное количество усилий.
Как и в большинстве классических алгоритмов трассировки лучей, при трассировке путей мы испускаем лучи из позиции камеры на сцену, и смотрим, с чем каждый из них сталкивается. По сути, мы "трассируем путь" фотона, прошедшего от источника света до нашего глаза, но только делаем это в обратную сторону, начиная от позиции наблюдателя (ведь нет смысла рассчитывать свет, который в итоге не дойдет до нашего глаза).

Одним из первых вопросов, которым можно задаться при рассмотрении данного алгоритма: а до какого вообще момента нам нужно моделировать движение луча? С точки зрения физики, практически каждый объект, что нас окружает, отражает хоть сколько-то света. Соответственно, естественный способ моделирования пути фотона - вычисление траектории движения вплоть до тех пор, пока количество отраженного света от объекта станет настолько малым, что им можно пренебречь. Такой метод безусловно имеет место быть, однако является крайне непроизводительным, и поэтому в любом трассирующем лучи алгоритме все же приходится жертвовать физической достоверностью изображения ради получения картинки за хоть сколько-то вменяемое время. Чаще всего выбор числа отражений луча зависит от сцены - для грубых диффузных поверхностей требуется гораздо меньше итераций, нежели для зеркальных или металлических (можете вспомнить классический пример с двумя зеркалами в лифте - свет в них отражается огромное число раз, создавая эффект бесконечного туннеля, и мы должны уметь это моделировать).

Другой вопрос, который у нас возникает - какие объекты могут быть на нашей сцене, и какими свойствами они обладают. И тут уже все не так очевидно и чаще всего зависит от конкретной реализации трассировщика. Для примера: в классическом физически-корректном рендеринге для описания объектов используют заранее заготовленный материалы с варьирующимися параметрами: албедо (диффузная отражательная способность материала), шероховатость (параметр, аппроксимирующий неровности поверхности на микро-уровне) и металличность (параметр, задающий отражательную способность материала). Иногда к ним добавляют и другие свойства, такие как прозрачность и показатель преломления.
Я же для своего алгоритма решил условно выделить для материала объекта следующие параметры:
Отражательная способность (reflectance) - какое количество и какой волны свет отражает каждый объект
Шероховатость поверхности (roughness) - насколько сильно лучи рассеиваются при столкновении с объектом
Излучение энергии (emittance) - количество и длина волны света, которую излучает объект
Прозрачность (transparency/opacity) - отношение пропущенного сквозь объект света к отраженному
В принципе, этих параметров достаточно, чтобы смоделировать источники света, зеркальные и стеклянные поверхности, а также диффузные материалы, поэтому я решил, что на данный момент лучше остановиться на них и сохранить простоту получившегося трассировщика.
Реализуем наш алгоритм на GLSL
К сожалению (или к счастью?) сегодня мы не будем делать профессиональный трассировщик путей, и ограничимся лишь базовым алгоритмом с возможностью трассировать на сцене параллелепипеды и сферы. Для них относительно легко находить пересечения c лучем, рассчитывать нормали, да и в целом такого набора примитивов уже достаточно, чтобы отрендерить классический cornell-box.

Основной алгоритм мы будем делать во фрагментном GLSL шейдере. В принципе, даже если вы не знакомы с самим языком, код будет достаточно понятным, так как во многом совпадает с языком С: в нашем распоряжении есть функции и структуры, возможность писать условные конструкции и циклы, и ко всему прочему добавляется возможность пользоваться встроенными примитивами для математических расчетов - vec2, vec3, mat3 и т.д.
Ну что же, давайте к коду! Для начала зададим наши примитивы и структуру материала:
struct Material
{
vec3 emmitance;
vec3 reflectance;
float roughness;
float opacity;
};
struct Box
{
Material material;
vec3 halfSize;
mat3 rotation;
vec3 position;
};
struct Sphere
{
Material material;
vec3 position;
float radius;
};Для примитивов реализуем проверки пересечения с лучем: будем принимать начало луча и его направление, а возвращать расстояние до ближайшей точки пересечения и нормаль объекта в этой точке, если, конечно, такое пересечение в принципе произошло:
bool IntersectRaySphere(vec3 origin, vec3 direction, Sphere sphere, out float fraction, out vec3 normal)
{
vec3 L = origin - sphere.position;
float a = dot(direction, direction);
float b = 2.0 * dot(L, direction);
float c = dot(L, L) - sphere.radius * sphere.radius;
float D = b * b - 4 * a * c;
if (D < 0.0) return false;
float r1 = (-b - sqrt(D)) / (2.0 * a);
float r2 = (-b + sqrt(D)) / (2.0 * a);
if (r1 > 0.0)
fraction = r1;
else if (r2 > 0.0)
fraction = r2;
else
return false;
normal = normalize(direction * fraction + L);
return true;
}
bool IntersectRayBox(vec3 origin, vec3 direction, Box box, out float fraction, out vec3 normal)
{
vec3 rd = box.rotation * direction;
vec3 ro = box.rotation * (origin - box.position);
vec3 m = vec3(1.0) / rd;
vec3 s = vec3((rd.x < 0.0) ? 1.0 : -1.0,
(rd.y < 0.0) ? 1.0 : -1.0,
(rd.z < 0.0) ? 1.0 : -1.0);
vec3 t1 = m * (-ro + s * box.halfSize);
vec3 t2 = m * (-ro - s * box.halfSize);
float tN = max(max(t1.x, t1.y), t1.z);
float tF = min(min(t2.x, t2.y), t2.z);
if (tN > tF || tF < 0.0) return false;
mat3 txi = transpose(box.rotation);
if (t1.x > t1.y && t1.x > t1.z)
normal = txi[0] * s.x;
else if (t1.y > t1.z)
normal = txi[1] * s.y;
else
normal = txi[2] * s.z;
fraction = tN;
return true;
}В рамках данной статьи мы не будем вдаваться в реализацию алгоритмов пересечений - это расписано уже много-много раз. В частности, код двух функций, приведенных в блоке выше, я нагло взял с этого сайта.
Хранить все наши объекты будем в обычных массивах, благо, GLSL создавать их также позволяет. Сцена у нас небольшая, поэтому никаких оптимизаций при поиске пересечения не реализуем - просто проходим по всем объектам и вычисляем ближайшее расстояние до точки пересечения:
#define FAR_DISTANCE 1000000.0
#define SPHERE_COUNT 3
#define BOX_COUNT 8
Sphere spheres[SPHERE_COUNT];
Box boxes[BOX_COUNT];
bool CastRay(vec3 rayOrigin, vec3 rayDirection, out float fraction, out vec3 normal, out Material material)
{
float minDistance = FAR_DISTANCE;
for (int i = 0; i < SPHERE_COUNT; i++)
{
float D;
vec3 N;
if (IntersectRaySphere(rayOrigin, rayDirection, spheres[i], D, N) && D < minDistance)
{
minDistance = D;
normal = N;
material = spheres[i].material;
}
}
for (int i = 0; i < BOX_COUNT; i++)
{
float D;
vec3 N;
if (IntersectRayBox(rayOrigin, rayDirection, boxes[i], D, N) && D < minDistance)
{
minDistance = D;
normal = N;
material = boxes[i].material;
}
}
fraction = minDistance;
return minDistance != FAR_DISTANCE;
}Функция выше позволяет нам найти точку столкновения луча с поверхностью. Это работает, но мы получаем информацию только о прямом освещении. Мы же хотим учитывать еще и непрямое освещение, поэтому давайте немного подумаем над тем, как меняется поток света при столкновениях с объектами на нашей сцене.
Трассировка пути
В нашей реализации каждый объект может излучать свет, отражать свет, и поглощать (случай с преломлением пока опустим). В таком случае формулу для расчета отраженного света от поверхности можно задать следующим образом: L' = E + f*L, где E - излучаемый объектом свет (emittance), f - отражаемый объектом свет (reflectance), L - свет, упавший на объект, и L' - то, что объект в итоге излучает. Выводя эту зависимость, мы опираемся исключительно на нашу логику относительно поведения света, но если вас интересует математическая корректность приведенного мной выражения, посмотрите уравнение рендеринга, оно хоть и выглядеть гораздо сложнее, но по сути заключает в себе те же вычисления, что мы с вами сейчас проводим.
Так или иначе, воплотим наши мысли в жизнь с помощью следующего итеративного алгоритма:
// максимальное количество отражений луча
#define MAX_DEPTH 8
vec3 TracePath(vec3 rayOrigin, vec3 rayDirection)
{
vec3 L = vec3(0.0); // суммарное количество света
vec3 F = vec3(1.0); // коэффициент отражения
for (int i = 0; i < MAX_DEPTH; i++)
{
float fraction;
vec3 normal;
Material material;
bool hit = CastRay(rayOrigin, rayDirection, fraction, normal, material);
if (hit)
{
vec3 newRayOrigin = rayOrigin + fraction * rayDirection;
vec3 newRayDirection = ...
// рассчитываем, куда отразится луч
rayDirection = newRayDirection;
rayOrigin = newRayOrigin;
L += F * material.emmitance;
F *= material.reflectance;
}
else
{
// если столкновения не произошло - свет ничто не испускает
F = vec3(0.0);
}
}
// возвращаем суммарный вклад освещения
return L;
}Если бы мы писали наш код на условном C++, можно было бы напрямую получать L как результат работы рекурсивно вызываемой функции CastRay. Однако, GLSL не разрешает рекурсивные вызовы функций в любом виде, поэтому приходится развернуть наш алгоритм так, чтобы он работал итеративно. С каждым отражением мы уменьшаем коэффициент, на который умножается испускаемый или отражаемый объектом свет, и тем самым повторяем описанную выше формулу. В моей реализации потенциально каждый объект может излучать какое-то количество света, поэтому emittance учитывается при каждом столкновении. Если же луч ни с чем не сталкивается, мы считаем, что никакого света до нас не дошло. В принципе для таких случаев можно добавить выборку из карты окружения или задать "дневной свет", но после экспериментов с этим я понял, что больше всего мне нравится текущая реализация, с пустотой вокруг сцены.
Об отражениях
Теперь давайте решим следующий вопрос: а по какому же принципу луч отражается от объекта? Очевидно, что в нашем path-tracer'е это будет зависеть от нормали в точке падения и микро-рельефа поверхности. Если обратиться к реальному миру, мы увидим, что для гладких материалов (таких как отполированный металл, стекло, вода) отражение будет очень четким, так как все лучи, падающие на объект под одним углом, будут и отражаться примерно под одинаковым углом (см. specular на картинке ниже), когда как для шероховатых, неровных поверхностей мы наблюдаем очень размытые отражения, чаще всего диффузные (см. diffuse на картинке ниже), так как лучи распространяются по полусфере относительно нормали объекта. Именно этой закономерностью мы и воспользуемся, задав итоговое направление отраженного луча как D = normalize(a * R + (1 - a) * T), где a - коэффициент шероховатости/гладкости поверхности, R - идеально отраженный луч, T - луч, отраженный в случаном направлении в полусфере относительно нормали. Очевидно, что при коэффициенте a = 1 в такой формуле мы всегда будет получать идеальное отражение луча, а при a = 0, наоборот, равномерно распределенное по полусфере. При коэффициенте шероховатости, лежащем в интервале от 0 до 1, на выходе будем иметь некоторое распределение лучей, ориентированное по углу отражения, что в вполне корректно и как раз характерно для глянцевых поверхностей (см. glossy на картинке ниже).
Вернемся к коду. Давайте начнем в этот раз с самого сложного - напишем реализацию функции, которая бы возвращала нам случайный луч в полусфере относительно нормали. Для этого сначала возьмем какой-нибудь набор случайно распределенных чисел, и сгенерируем по ним луч, лежащий в на границе полусферы единичного радиуса с учетом косинус-взвешенного распределения, а затем тривиальным образом спроецируем его в ту же полусферу, где находится нормаль объекта:
#define PI 3.1415926535
vec3 RandomHemispherePoint(vec2 rand)
{
float cosTheta = sqrt(1.0 - rand.x);
float sinTheta = sqrt(rand.x);
float phi = 2.0 * PI * rand.y;
return vec3(
cos(phi) * sinTheta,
sin(phi) * sinTheta,
cosTheta
);
}
vec3 NormalOrientedHemispherePoint(vec2 rand, vec3 n)
{
vec3 v = RandomHemispherePoint(rand);
return dot(v, n) < 0.0 ? -v : v;
}Не забываем: сгенерированный нами луч хоть и лежит в одной полусфере с нормалью, но множество таких случайных лучей все еще не ориентировано под нужным нам углом. Чтобы это исправить, давайте спроецируем их в пространство нормали: зададим еще один случайный вектор, затем найдем третий через векторное произведение, и соединим их всех в матрицу трансформации:
vec3 hemisphereDistributedDirection = NormalOrientedHemispherePoint(Random2D(), normal);
vec3 randomVec = normalize(2.0 * Random3D() - 1.0);
vec3 tangent = cross(randomVec, normal);
vec3 bitangent = cross(normal, tangent);
mat3 transform = mat3(tangent, bitangent, normal);
vec3 newRayDirection = transform * hemisphereDistributedDirection;Небольшое примечание: здесь и далее Random?D генерирует случайные числа в интервале от 0 до 1. В GLSL шейдере делать это можно разными способами. Я использую следующую функцию, генерирующую случайным шум без явных паттернов (любезно взята со StackOverflow по первому запросу):
float RandomNoise(vec2 co)
{
return fract(sin(dot(co.xy, vec2(12.9898, 78.233))) * 43758.5453);
}В комбинации с такими параметрами как координатой текущего пикселя (gl_FragCoord), временем работы приложения, и еще какими-то независимыми переменными можно сгенерировать достаточно много псевдослучайных чисел. Вы также можете пойти иначе и просто передавать массив случайных чисел в шейдер, но это уже дело вкуса.
После всех наших модификаций код нашей функции TracePath будет выглядеть вот так:
vec3 TracePath(vec3 rayOrigin, vec3 rayDirection)
{
vec3 L = vec3(0.0);
vec3 F = vec3(1.0);
for (int i = 0; i < MAX_DEPTH; i++)
{
float fraction;
vec3 normal;
Material material;
bool hit = CastRay(rayOrigin, rayDirection, fraction, normal, material);
if (hit)
{
vec3 newRayOrigin = rayOrigin + fraction * rayDirection;
vec3 hemisphereDistributedDirection = NormalOrientedHemispherePoint(Random2D(), normal);
randomVec = normalize(2.0 * Random3D() - 1.0);
vec3 tangent = cross(randomVec, normal);
vec3 bitangent = cross(normal, tangent);
mat3 transform = mat3(tangent, bitangent, normal);
vec3 newRayDirection = transform * hemisphereDistributedDirection;
vec3 idealReflection = reflect(rayDirection, normal);
newRayDirection = normalize(mix(newRayDirection, idealReflection, material.roughness));
// добавим небольшое смещение к позиции отраженного луча
// константа 0.8 тут взята произвольно
// главное, чтобы луч случайно не пересекался с тем же объектом, от которого отразился
newRayOrigin += normal * 0.8;
rayDirection = newRayDirection;
rayOrigin = newRayOrigin;
L += F * material.emmitance;
F *= material.reflectance;
}
else
{
F = vec3(0.0);
}
}
return L;
}Преломление света
Давайте рассмотрим еще такой важный для нас эффект, как преломление света. Все же помнят, как соломка, находящаяся в стакане, кажется сломанной в том месте, где она пересекается с водой? Этот эффект происходит потому, что свет, переходя между двумя средами с разными свойствами, меняет свою волновую скорость. Вдаваться в подробности того, как это работает с физической точки зрения мы не будем, вспомним лишь, что если свет падаем под углом a, то угол преломления b можно посчитать по следующей несложной формуле (см. закон Снеллиуса): b = arcsin(sin(a) * n1 / n2), где n1 - показатель преломления среды, из которой пришел луч, a n2 - показатель преломления среды, в которую луч вошел. И к счастью для нас, показатели преломления уже рассчитаны для интересующих нас сред, достаточно лишь открыть википедию, или, накрайняк, учебник по физике.
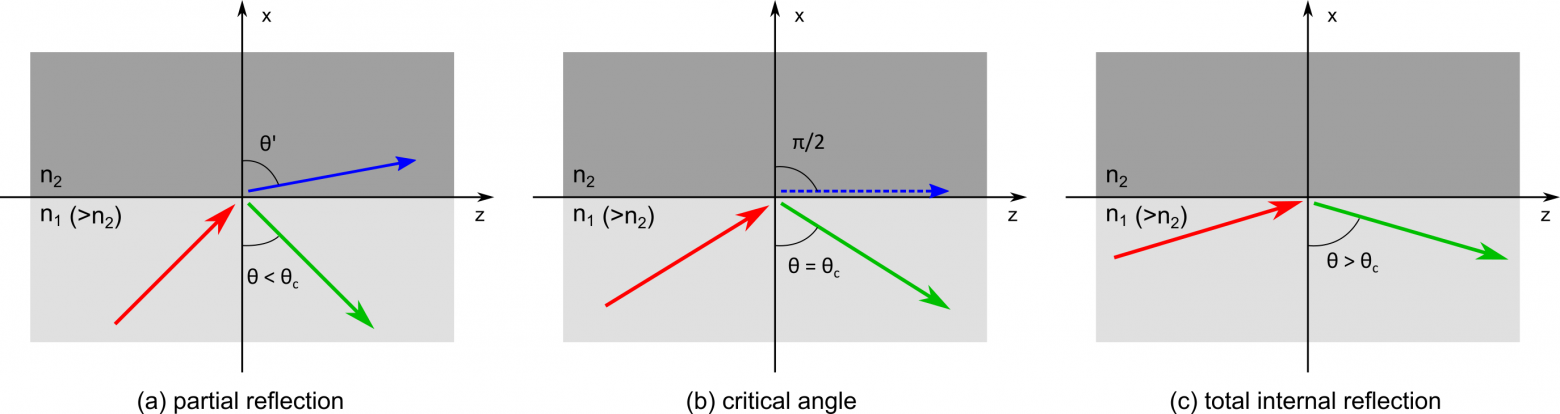
Стоит заметить следующий интересный факт: sin(a) принимает значения от 0 для 1 для острых углов. Относительный показатель преломления n1 / n2 может быть любым, в том числе большим 1. Но тогда выходит, что аргумент sin(a) * n1 / n2 не всегда находится в области определения функции arcsin. Что же происходит с углом преломления? Почему наша формула не работает для такого случая, хотя с физической точки зрения ситуация вполне возможная?
Ответ кроется в том, что в реальном мире при таких условиях луч света попросту не преломится, а отразится! Данный эффект абсолютно логичен, если вспомнить, что в момент столкновения луча с границей раздела двух сред, он по сути "делится на двое", и лишь часть света преломляется, когда как остальная отражается. И с увеличением наклона под которым падает этот луч, все больше и больше света будет отражаться, пока не дойдет до того вырожденного, критического момента. Данное явление в физике носит название внутреннее отражение, а частный его случай, когда абсолютно весь свет отражается от границы раздела сред, называется полным внутренним отражением. И этот факт нужно будет учитывать в реализации нашего трассировщика путей.

Сколько же света в итоге будет отражено от поверхности, а сколько пройдет сквозь нее? Чтобы ответить на этот вопрос, нам необходимо обратиться к формулам Френеля, которые как раз и используются для расчета коэфициентов отрадения и пропускания. Но не спешите ужасаться - в нашем трассировщике мы не будем расписывать эти громоздкие выражения. Давайте воспользуемся более простой аппроксимирующей формулой за авторством Кристофе Шлика - аппроксимацией Шлика. Она достаточно простая в реализации и дает приемлимые визуальные результаты, поэтому не вижу причин не добавить ее в наш код:
float FresnelSchlick(float nIn, float nOut, vec3 direction, vec3 normal)
{
float R0 = ((nOut - nIn) * (nOut - nIn)) / ((nOut + nIn) * (nOut + nIn));
float fresnel = R0 + (1.0 - R0) * pow((1.0 - abs(dot(direction, normal))), 5.0);
return fresnel;
}Ну что же, применим весь наш пройденный материал: первым делом реализуем функцию, которая бы возвращала преломленный луч с учетом полного внутреннего отражения, о котором мы говорили выше:
vec3 IdealRefract(vec3 direction, vec3 normal, float nIn, float nOut)
{
// проверим, находимся ли мы внутри объекта
// если да - учтем это при расчете сред и направления луча
bool fromOutside = dot(normal, direction) < 0.0;
float ratio = fromOutside ? nOut / nIn : nIn / nOut;
vec3 refraction, reflection;
refraction = fromOutside ? refract(direction, normal, ratio) : -refract(-direction, normal, ratio);
reflection = reflect(direction, normal);
// в случае полного внутренного отражения refract вернет нам 0.0
return refraction == vec3(0.0) ? reflection : refraction;
}Чтобы учитывать эффект Френеля, будем просто генерировать случайное число, и на его основе решать, преломится ли луч или отразится. Также не забываем, что у наших объектов есть параметр плотности, который также отвечает за отношение преломленного света к отраженному. Соединить оба этих условия можно по-разному, но я взял самый примитивный вариант:
bool IsRefracted(float rand, vec3 direction, vec3 normal, float opacity, float nIn, float nOut)
{
float fresnel = FresnelSchlick(nIn, nOut, direction, normal);
return opacity > rand && fresnel < rand;
}Теперь наконец можно склеить все вместе: добавим в нашу функцию TracePath логику, которая бы рассчитывала преломление света и при этом учитывала и шереховатость объекта - ее для полупрозрачных тел никто не отменял:
#define N_IN 0.99
#define N_OUT 1.0
vec3 TracePath(vec3 rayOrigin, vec3 rayDirection)
{
vec3 L = vec3(0.0);
vec3 F = vec3(1.0);
for (int i = 0; i < MAX_DEPTH; i++)
{
float fraction;
vec3 normal;
Material material;
bool hit = CastRay(rayOrigin, rayDirection, fraction, normal, material);
if (hit)
{
vec3 newRayOrigin = rayOrigin + fraction * rayDirection;
vec3 hemisphereDistributedDirection = NormalOrientedHemispherePoint(Random2D(), normal);
randomVec = normalize(2.0 * Random3D() - 1.0);
vec3 tangent = cross(randomVec, normal);
vec3 bitangent = cross(normal, tangent);
mat3 transform = mat3(tangent, bitangent, normal);
vec3 newRayDirection = transform * hemisphereDistributedDirection;
// проверяем, преломится ли луч. Если да, то меняем логику расчета итогового направления
bool refracted = IsRefracted(Random1D(), rayDirection, normal, material.opacity, N_IN, N_OUT);
if (refracted)
{
vec3 idealRefraction = IdealRefract(rayDirection, normal, N_IN, N_OUT);
newRayDirection = normalize(mix(-newRayDirection, idealRefraction, material.roughness));
newRayOrigin += normal * (dot(newRayDirection, normal) < 0.0 ? -0.8 : 0.8);
}
else
{
vec3 idealReflection = reflect(rayDirection, normal);
newRayDirection = normalize(mix(newRayDirection, idealReflection, material.roughness));
newRayOrigin += normal * 0.8;
}
rayDirection = newRayDirection;
rayOrigin = newRayOrigin;
L += F * material.emmitance;
F *= material.reflectance;
}
else
{
F = vec3(0.0);
}
}
return L;
}Для коэффициентов преломления N_IN и N_OUT я взял два очень близких числа. Это не совсем физически-корректно, однако создает желаемый эффект того, что поверхности сделаны из стекла (как шар на первом скриншоте статьи). Можете смело их изменить и посмотреть, как поменяется угол преломления лучей, проходящих сквозь объект.
Давайте уже запускать лучи!
Дело осталось за малым: инициализировать нашу сцену в начале шейдера, передать внутрь все параметры камеры, и запустить лучи по направлению взгляда. Начнем с камеры: от нее нам потребуется несколько параметров: direction - направление взгляда в трехмерном пространстве. up - направление "вверх" относительно взгляда (нужен чтобы задать матрицу перевода в мировое пространство), а также fov - угол обзора камеры. Также передадим для расчета чисто утилитарные вещи - экранную позицию обрабатываемого пикселя (от 0 до 1 по x и y) и размер окна для расчета отношения сторон. В математику в коде тоже особо углубляться не буду - о том, как переводить из пространство экрана в пространство мира можно почитать к примеру в этой замечательной статье.
vec3 GetRayDirection(vec2 texcoord, vec2 viewportSize, float fov, vec3 direction, vec3 up)
{
vec2 texDiff = 0.5 * vec2(1.0 - 2.0 * texcoord.x, 2.0 * texcoord.y - 1.0);
vec2 angleDiff = texDiff * vec2(viewportSize.x / viewportSize.y, 1.0) * tan(fov * 0.5);
vec3 rayDirection = normalize(vec3(angleDiff, 1.0f));
vec3 right = normalize(cross(up, direction));
mat3 viewToWorld = mat3(
right,
up,
direction
);
return viewToWorld * rayDirection;
}Как бы ни прискорбно это было заявлять, но законы, по которым отражаются наши лучи имеют некоторую случайность, и одного семпла на пиксель нам будет мало. И даже 16 семплов на пиксель не достаточно. Но не расстраивайтесь! Давайте найдем компромисс: каждый кадр будем считать от 4 до 16 лучей, но при этом результаты кадров аккумулировать в одну текстуру. В итоге мы делаем не так много работы каждый кадр, можем летать по нашей сцене (хоть и испытывая на своих глазах ужасные шумы), а при статичной картинке качество рендера будет постепенно расти, пока не упрется в точность float'а. Преимущества такого подхода видны невооруженным взглядом:

В итоге наша функция main будет выглядеть примерно следующим образом (в алгоритме нет ничего сложного - просто запускаем несколько лучей и считаем среднее от результата TracePath):
// ray_tracing_fragment.glsl
in vec2 TexCoord;
out vec4 OutColor;
uniform vec2 uViewportSize;
uniform float uFOV;
uniform vec3 uDirection;
uniform vec3 uUp;
uniform float uSamples;
void main()
{
// заполняем нашу сцену объектами
InitializeScene();
vec3 direction = GetRayDirection(TexCoord, uViewportSize, uFOV, uDirection, uUp);
vec3 totalColor = vec3(0.0);
for (int i = 0; i < uSamples; i++)
{
vec3 sampleColor = TracePath(uPosition, direction);
totalColor += sampleColor;
}
vec3 outputColor = totalColor / float(uSamples);
OutColor = vec4(outputColor, 1.0);
}Аккумулируем!
Давайте закроем вопрос с тем, как мы будем отображать результат работы трассировщика. Очевидно, что если мы решили накапливать кадры в одной текстуре, то классический вариант с форматом вида RGB (по байту на каждый канал) нам не подойдет. Лучше взять что-то вроде RGB32F (проще говоря формат, поддерживающий числа с плавающей точкой одинарной точности). Таким образом мы сможем накапливать достаточно большое количество кадров прежде чем упремся в потолок из-за потерь точности вычислений.
Также сходу напишем шейдер, принимающий нашу аккумулирующую текстуру и вычисляющий среднее от множества кадров. Тут же применим тональную коррекцию изображения, а затем гамма-коррекцию (в коде я использую самый простой вариант tone-mapping'а, вы можете взять что-то посложнее, к примеру кривую Рейнгарда):
// post_process_fragment.glsl
in vec2 TexCoord;
out vec4 OutColor;
uniform sampler2D uImage;
uniform int uImageSamples;
void main()
{
vec3 color = texture(uImage, TexCoord).rgb;
color /= float(uImageSamples);
color = color / (color + vec3(1.0));
color = pow(color, vec3(1.0 / 2.2));
OutColor = vec4(color, 1.0);
}И на этом часть с GLSL кодом можно считать оконченной. Как будет выглядеть наш трассировщий снаружи - вопрос открытый и зависит полностью от вас. Ниже я конечно же приведу реализацию рендеринга в контексте API моего движка, на котором я и писал данный трассировщик, но информация эта скорее опциональная. Думаю вам не составит труда написать связующий код на том фреймворке или графическом API, с которым лично вам удобнее всего работать:
virtual void OnUpdate() override
{
// получаем текущую камеру и текстуру, в которую осуществляется рендер
auto viewport = Rendering::GetViewport();
auto output = viewport->GetRenderTexture();
// получим текущие параметры камеры (позицию, угол обзора и т.д.)
auto viewportSize = Rendering::GetViewportSize();
auto cameraPosition = MxObject::GetByComponent(*viewport).Transform.GetPosition();
auto cameraRotation = Vector2{ viewport->GetHorizontalAngle(), viewport->GetVerticalAngle() };
auto cameraDirection = viewport->GetDirection();
auto cameraUpVector = viewport->GetDirectionUp();
auto cameraFOV = viewport->GetCamera<PerspectiveCamera>().GetFOV();
// проверим, что камера неподвижна. От этого зависит, нужно ли очищать предыдущий кадр
bool accumulateImage = oldCameraPosition == cameraPosition &&
oldCameraDirection == cameraDirection &&
oldFOV == cameraFOV;
// при движении снизим количество семплов ради приемлемой частоты кадров
int raySamples = accumulateImage ? 16 : 4;
// установим все униформы в шейдере, осуществляющем трассировку лучей
this->rayTracingShader->SetUniformInt("uSamples", raySamples);
this->rayTracingShader->SetUniformVec2("uViewportSize", viewportSize);
this->rayTracingShader->SetUniformVec3("uPosition", cameraPosition);
this->rayTracingShader->SetUniformVec3("uDirection", cameraDirection);
this->rayTracingShader->SetUniformVec3("uUp", cameraUpVector);
this->rayTracingShader->SetUniformFloat("uFOV", Radians(cameraFOV));
// меняем тип блендинга в зависимости от того, аккумулируем ли мы кадры в одну текстуру
// также считаем количество кадров, чтобы потом получить среднее значение
if (accumulateImage)
{
Rendering::GetController().GetRenderEngine().UseBlending(BlendFactor::ONE, BlendFactor::ONE);
Rendering::GetController().RenderToTextureNoClear(this->accumulationTexture, this->rayTracingShader);
accumulationFrames++;
}
else
{
Rendering::GetController().GetRenderEngine().UseBlending(BlendFactor::ONE, BlendFactor::ZERO);
Rendering::GetController().RenderToTexture(this->accumulationTexture, this->rayTracingShader);
accumulationFrames = 1;
}
// рассчитаем среднее от множества кадров и сохраним в рендер-текстуру камеры
this->accumulationTexture->Bind(0);
this->postProcessShader->SetUniformInt("uImage", this->accumulationTexture->GetBoundId());
this->postProcessShader->SetUniformInt("uImageSamples", this->accumulationFrames);
Rendering::GetController().RenderToTexture(output, this->postProcessShader);
// обновим сохраненные параметры камеры
this->oldCameraDirection = cameraDirection;
this->oldCameraPosition = cameraPosition;
this->oldFOV = cameraFOV;
}В заключение
Ну что же, на этом все! Всем спасибо за прочтение этой небольшой статьи. Хоть мы и не успели рассмотреть множество интересных эффектов в path-tracing'е, опустили обсуждение различных ускоряющих трассировку структур данных, не сделали денойзинг, но все равно итоговый результат получился весьма сносным. Надеюсь вам понравилось и вы нашли для себя что-то новое. Я же по традиции приведу в конце несколько скриншотов, полученных с помощью path-tracer'а:



Ссылки на связанные ресурсы
Исходный код Path-Tracer'а можно найти на GitHub: https://github.com/MomoDeve/PathTracer
Мой основной проект, над которым я сейчас работаю: игровой движок MxEngine
Крутая статья от @haqreu на смежную тему о рейтрейсинге: https://habr.com/ru/post/436790
О физически-корректном рендеринге, importance-sampling'е и много о чем еще от @MrShoor: https://habr.com/ru/post/326852/