This is the next article in the series Algorithms in Go. In this part, we discuss the postorder traversal of a binary tree. What does postorder traversal mean? It means that at first, we process the left subtree of the node, then the right subtree of the node, and only after that we process the node itself.
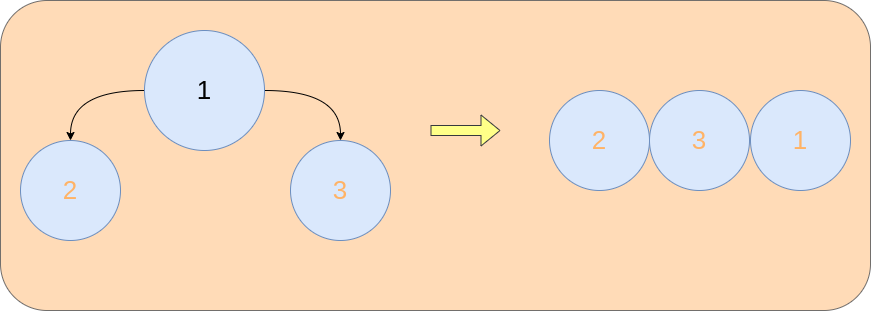
Why would we need to do it in this order? This approach solves an entire class of algorithmic problems related to the binary trees. For example, to find the longest path between two nodes we need to traverse the tree in a postorder manner. In general, postorder traversal is needed when we cannot process the node without processing its children first. In this manner, for example, we can calculate the height of the tree. To know the height of a node, we need to calculate the height of its children and increment it by one.
Let's start with a recursive approach. We need to process the left child, then the right child and finally we can process the node itself. For simplicity, let's just save the values into slice out.
var out []int
var f func(root *TreeNode)
f = func(root *TreeNode) {
if root == nil {
return
}
f(root.Left)
f(root.Right)
out = append(out, root.Val)
}In this case, the recursive function pretty much embodies the definition of the postorder traversal. We deal with the left subtree, then the right subtree and finally process the root value.
Now, how can we convert this function into an iterative version?
We can solve this problem with the following approach:
Push the root node into the stack.
Push the left child into the stack.
Pop the left child from the stack and process it.
Push the right child into the stack.
Pop the right child from the stack and process it
Pop the root node and process it.
Let's consider the following tree:
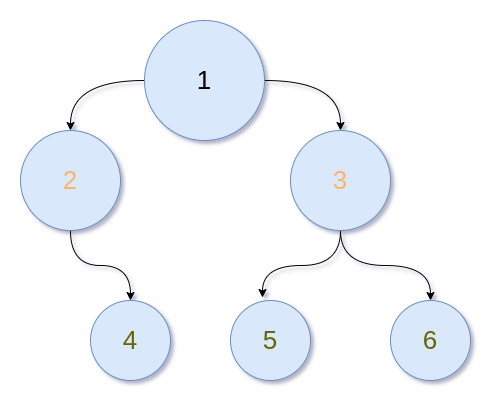
We push the root node 1into the stack. At the next step, we put its left child 2 into the stack.

At the next iteration, we have node 2 at the top of the stack, therefore we try to put its left child into the stack. As the left child is not present, we skip this step and push its right child 4 into the stack.

After this stage, we have three nodes in our stack. The top node 4 does not have any children, so we process its value and pop it from the stack.

Now, we have the same nodes in the stack as at the previous step. However, we have already processed all children of the node 2, therefore we can process node 2 and pop it from the stack.
After this iteration, we have a single node in the stack which is node 1. We haven't processed its right child yet, so we put it into the stack. We proceed in the same manner and process the right subtree of node 1.
How can we encode this algorithm? We need to have some check that ensures that we don't process a node twice. When we process a node, there are two possible situations:
We just met this node and need to push its children into the stack.
We have already processed its children and now are returning back to process the node itself.
We can save the last processed node into the variable prev. If the right child of the current node is equal to prev it means that we already processed both of its children and now need to process the value of the current node. For the left child, we need to check one more condition: it is possible that the current node doesn't have the right child. In this case, we need to check whether prev node is equal to the left child. If that's the case, then we already processed the left child of the current node and we don't have the right child at all, therefore we can process the value of the current node.
Let's encode this algorithm in Go
var out []int
prev := root
stack := []*TreeNode{root}
for len(stack) > 0 {
node := stack[len(stack)-1]
if node.Left != nil && node.Left != prev && node.Right != prev {
stack = append(stack, node.Left)
} else if node.Right != nil && node.Right != prev {
stack = append(stack, node.Right)
} else {
prev = node
stack = stack[:len(stack)-1]
out = append(out, node.Val)
}
}
return outIn this post, we implemented the postorder traversal of the binary tree. This is one of the most popular algorithmic patterns that solve an entire class of problems. More algorithmic patterns such as Sliding Window or Matrix Spiral can be found in the series Algorithms in Go.