Comments 4
Спасибо за статью.
Но непонятно два момента ;)
Во первых, почему решений только 4, если их значительно больше - BACD, BADC, BCAD, BDAC, CABD, CADB, CBAD, CDAB, DABC, DACB, DBAC, DCAB?
Во вторых - почему алгоритм нашел два решения с первой вершиной "C", но только по одному для "B" и "D", хотя граф симметричный относительно B, C и D?
Спасибо за комментарий! Обнаружил ошибки невнимательности при подготовке иллюстраций: в изображении графа ошибочно соединил вершины A и B, хотя изначально задача сформулирована и решена для случая, когда этой связи нет.
Изображения поправил, теперь должно быть видно, что решений всего 4 и симметрии относительно вершин нет.
удалено
Спасибо за статью, очень познавательно.
В формуле числа итераций, мне кажется, ошибка. Под корнем вместо n (число кубитов) должно быть N/K, где N - число всех возможных состояний и K - число искомых состояний (в примере из статьи это 4), причем эта формула оценочная и только для больших N, а в этом примере можно число итераций посчитать напрямую через угол между гиперплоскостью всех состояний кроме искомых и гиперплоскостью искомых состояний. Если этот угол поставить в формулу (2i + 1)*угол (где i - число итераций), то должно получиться около 90 градусов, для того, чтобы при измерении получались в основном только искомые состояния.
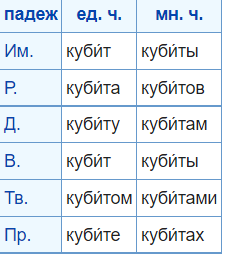
И еще по поводу слова "кубит" - оно склоняется по падежам (https://ru.wiktionary.org/wiki/кубит):
Применение алгоритма Гровера для поиска гамильтоновых циклов в графе