alectroid Nov 29 2021 at 23:39

Теория графов в криптографии. Обзор основных подходов

9 min

5.4K

Введение

Теория графов - один из основных инструментов математики, который используется для представления множеств и связей между ними. Любая сфера науки, в том числе криптография, включает в себя анализ данных, поэтому модель имеет широкое практическое применение. В данной статье рассматриваются задачи из теории графов, которые лежат в основе современных криптографических протоколов.

Правильная раскраска графа в протоколах нулевого разглашения

Задача о правильной раскраске графа является одной известнейших проблем в области разметки графов. Формулируется она следующим образом: если дан граф

и количество цветов k (хроматическое число), то существует ли такая раскраска вершин графа G, при которой никакие две вершины, соединенные ребром, не были бы окрашены одним цветом?

Поиск хроматического числа, при котором данная задача разрешима, входит в класс NP-полных (т.е. решаемых не менее чем за полиномиальное время, что очень медленно). Более того, в данной работе было доказано, что при k=3 в случае планарного 4-регулярного графа доказать раскрашиваемость или ее отсутствие также можно не быстрее полиномиального времени. Поэтому даже 3-раскрашиваемость графа имеет большой интерес в криптографии и имеет практическое применение, к примеру, в протоколах нулевого разглашения.

Подробное описание задачи нулевого разглашения можно найти здесь. Если кратко, смысл заключается в доказательстве проверяющей стороне правильности утверждения без раскрытия самого алгоритма, с помощью которого ответ был получен. Идея протокола нулевого разглашения заключается в генерации последовательности итераций (сеансов связи), в результате каждой из которых контролер получает ответ на какой-либо вопрос. Этот вопрос не позволяет узнать решение задачи, но зато увеличивает вероятность того, что доказывающая сторона говорит правду. Завершением цикла является либо условие достижения некоторого количества последовательно верных ответов, либо получение ложного ответа, т.е. факт обмана.

Приведем пример. Пусть к студенту подходит школьник начальных классов и просит его решить квадратное уравнение. Из-за своего самолюбия, первый не желает раскрыть ребенку алгоритм нахождения дискриминанта, и потому просто диктует численный ответ. Но школьник хочет убедиться в том, что его не обманули. Тогда студент просит составить другое произвольное квадратное уравнение, чтобы повторить эксперимент. Если и в этот раз ребенок, подставив числа в выражение, получит тождество, то его степень доверия к человеку вырастет. Этот процесс генерации квадратных уравнений и его корней продолжается настолько долго, насколько требуется, чтобы убедить проверяющего в том, что источник достоверен. Важно отметить, что любой протокол нулевого разглашения должен удовлетворять трем свойствам:

Являться полным (порог доверия может быть задан сколь угодно близким к 100%).
Являться корректным (неправильный ответ приводит к потере доверия).
Иметь нулевое разглашение (проверяющий лишь убеждается в том, что ответы верные, но он ничего не узнает о том, как они получены).

Если алгоритм нахождения корней квадратного уравнения тривиален, то задача правильной раскраски графа NP-полна, потому ее решение для чрезмерно больших графов имеет коммерческую ценность. Предложим алгоритм нулевого разглашения на основе 3-раскрашиваемости с использованием распространенного протокола RSA.

Пусть доказывающая сторона, Алиса, знает правильную раскраску в три цвета {R, G, B} у фиксированного планарного 4-регулярного графа G. Она хочет доказать контролирующей стороне, Бобу, что знает верное решение (структура графа G ему известна).

Приведем картинку:

Планарный 4-регулярный граф с хроматическим числом k = 3

Алиса выбирает случайную перестановку цветов (пусть R окрашивается в B, G - в R, B - в G; получили из {R,G,B} {B,R,G}) и таким образом перекрашивает граф. Очевидно, что правильность раскраски при этом не нарушится.
Для каждой вершины Алиса формирует случайное число r и заменяет в нем два младших бита на 00 (R), 01(G), 10(B) соответственно.

Для каждой вершины Алиса формирует параметры для RSA.

$\forall v \in V \quad \exists P_v,Q_v, \quad N_v=P_vQ_v, \quad c_v,d_v$

и вычисляет

$Z_v=r_v^{d_v}\quad \text{mod}N_v$

для каждой вершины посылает Бобу значения

Теперь Боб случайно выбирает в графе G одно ребро и сообщает Алисе данные об этом ребре. В ответ Алиса высылает два числа:

$c_{v1}, c_{v2}$

На основе которых Боб вычисляет цвета вершин, которые соединены выбранным ребром:

$Z'_{v1}=Z_{v1}^{c_{v1}}\text{mod}N_{v1}=r_{v1}$ $Z'_{v2}=Z_{v2}^{c_{v2}}\text{mod}N_{v2}=r_{v2}$

Если два младших бита вычисленных r совпадают, то цвета вершин, соединенных ребром, одинаковы - это означает обман, связь прерывается. В противном величина вероятности лжи уменьшается на некоторое маленькое число. В случае последовательно верных ответов выше описанные действия повторяются некоторое число раз. К примеру, число итераций N можно задать через число ребер и произвольный параметр:

$N=a|E|,\ a>0,\ G=(V,E)$

Данный алгоритм удовлетворяет условию полноты. Вероятность того, что Алиса не разоблачена, составляет:

$P=(1-\frac{1}{|E|})^{a|E|} \le (e^{\frac{-1}{|E|}})^{a|E|}=e^{-a}\rightarrow_{a\rightarrow +\infty}0$

Важно отметить, что данный алгоритм удовлетворяет условию нулевого разглашения. Из-за того, что на каждой итерации цветовая палитра меняется, Боб, имея раскраску каждого ребра, не сможет подобно пазлу воссоздать правильную раскраску всего графа. Также нетрудно убедиться в том, что алгоритм является корректным.

Поиск гамильтонова цикла в графе

Согласно определению, гамильтонов цикл - замкнутый путь в графе, проходящий по каждому его ребру ровно один раз. Граф, имеющий такой цикл, называют гамильтоновым. Задача поиска гамильтонова цикла является NP-полной (см. в этой книге).

Если раскраска графа была иллюстрационным примером протокола нулевого разглашения, то задача поиска гамильтонова цикла лежит в основе его современной реализации.

Опишем идею алгоритма. Пусть Алиса знает гамильтонов цикл в графе Г и хочет доказать это Бобу (граф ему известен).

Алиса строит граф G, изоморфный графу Г. К примеру, она перенумеровывает вершины, сохраняя их первоначальные связи. Полученный граф представляется матрицей смежности H.
Матрица H шифруется в F, к примеру, по тому же алгоритму RSA:

$F_{ij}=(r_{ij}||H_{ij})^d \quad modN$

и отправляется Бобу.

Получив матрицу F (зашифрованный граф G), Боб задает Алисе один из двух вопросов:
- Какой гамильтонов цикл у графа G (а)?
- Действительно ли G изоморфен Г (б)?
На вопрос (а) Алиса расшифровывает в F ребра, соответствующие гамильтонову циклу в G. На вопрос (b) Алиса расшифровывает граф G полностью, а также предоставляет перестановки, с помощью которых из Г получился G.
Получив ответ, Боб проверяет правильность расшифровки путем повторного шифрования Г и сравнения с F. Таким образом, он убеждается либо в корректности гамильтонова цикла в G, либо в изоморфности графов Г и G. Далее, если обмана зафиксировано не было, увеличить степень доверия и перейти к началу.

Отметим важные аспекты данного протокола. Во-первых, зачем Алисе строить изоморфный граф? Ответ: без этого Боб, получив ответ на вопрос (a), узнал бы гамильтонов цикл в исходом графе Г, что противоречит условию нулевого разглашения.

Во-вторых, зачем Алиса кодирует матрицу смежности графа Г конкатенациями произвольных чисел r? Шифр RSA не позволяет закодировать 0 или 1, но их замена на два произвольных других числа - тоже ненадежно (можно легко провести биекцию между ними и нулем с единицей). Конкатенация со случайными r решит эту проблему. Более того по свойству RSA (он скрывает четность исходного числа) информация о младших битах коэффицииентов матрицы смежности H будет трудно расшифровать. Они и будут свидетельствовать о наличии или отсутствии ребра между вершинами.

В-третьих, зачем Бобу задавать два вопроса, а не ограничиться лишь первым? В таком случае Алиса смогла бы сгенерировать свой собственный граф с уже имеющимся гамильтоновым циклом и, очевидно, Боб не обнаружит никаких противоречий в том, что гамильтонов цикл существует и корректен.

В-четвертых, почему Боб не может задать одновременно два вопроса? Ответ очевидный: предоставленной информации будет достаточно, чтобы Боб смог сам восстановить гамильтонов цикл в исходном графе - это противоречит свойству нулевого разглашения.

Вероятность обмана на t итерациях не превосходит

$P=2^{-t}\rightarrow0$

Доказательство простое и основано на том, что пара вопросов образует бинарное дерево исходов. Подробное доказательство того, почему данный протокол является протоколом нулевого разглашения, можно прочитать тут.

Графы как представление обобщённых клеточных автоматов

Поиск псевдослучайных функций является важной задачей криптографии. Они используются в блочных шифрах (AES) и алгоритмах хеширования (SHA-3). Существуют критерии качества псевдослучайных функций: выполнение строгого лавинного эффекта, анализ на коллизии, степень нелинейности и др. Они в той или иной степени оценивают близость функции к случайной, для чего существуют стандартизированные пакеты тестов (NIST statistical test suit).

Существует множество подходов к построению псевдослучайных функций, один из которых основан на модели обобщенного клеточного автомата. Эта модель представляет собой конечное множество ячеек памяти, каждая из которых может принимать значение 0 или 1. То, каким будет значение ячейки на следующей итерации, зависит от других ячеек и задается локальной функцией связи. Входным значениями такой функции будет выступать начальный вектор памяти и номер итерации, а выходным - новый вектор памяти.

Данный подход широко распространен, т.к. он имеет простую аппаратную реализацию. Классическим примером клеточного автомата, используемого в криптографии, является линейный конгруэнтный генератор псевдослучайных чисел на основе регистра сдвига.

ГПСЧ на основе регистра сдвига (период не максимальный)

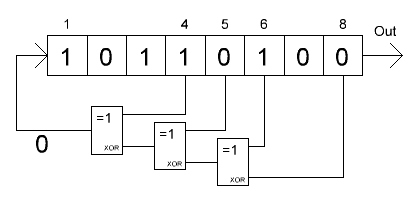
Можно заметить, что модель клеточного автомата легко представима в виде графа. Его вершинами являются ячейки памяти с заданными локальными функциями связи, число аргументов которых определяется наличием или отсутствием ребер.

Граф ГПСЧ на регистре сдвига с точки зрения клеточного автомата

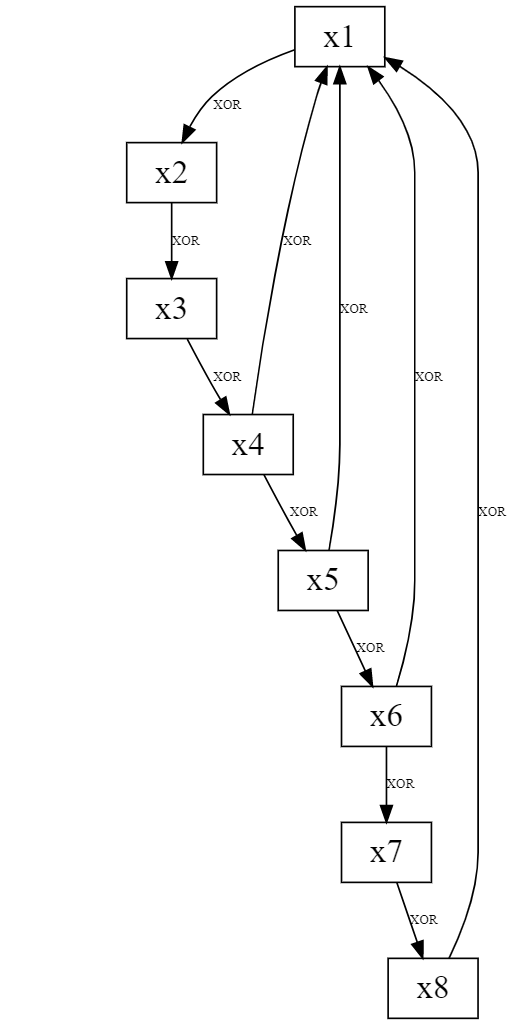
Таким образом, "качество" псевдослучайной функции в рамках рассматриваемой модели (клеточного автомата) будет определяться решением трех задач:

Как задать входные значения и номер итерации?
Какова структура графа обобщённого клеточного автомата?
Как задать локальные функции связи?

Подробные ответы на данные вопросы изложены здесь. В рамках заданной темы достаточно осветить второй пункт. Из соображений непредсказуемости и простоты аппаратной реализации граф должен удовлетворять следующим свойствам:

Быть приближенным к случайному (для псевдослучайности функции)
Иметь наименьший диаметр из теоретически возможных (для экономии аппаратных ресурсов)
Быть регулярным с минимальной степенью связности (для простоты задания локальных функций связи и повышения эффективности аппаратной реализации)
Не быть двудольным (для исключения быстрого рекурсивного разбиения на подграфы)
Быть масштабируемым на разное число ячеек памяти

Приведенным требованиям удовлетворяют графы Рамануджана. Подробно они изучаются в теории графов экспандеров и имеют множество приложений в науке. Согласно определению граф Рамануджана R - d-регулярный связный граф, для которого выполняется неравенство:

$\lambda(G) \le 2\sqrt{d-1}$

Здесь

$\lambda$

есть максимальный по модулю, но не равный d, компонент спектра R. Чем же R отличаются от других?

Из теории графов экспандеров следует, что чем больше коэффициент расширения графа экспандера, тем лучше характеристики лавинного эффекта. Однако вычисление этого коэффициента - трудная задача. Т.к. его значение ограничено

$0.5(d-\lambda_2) \le h(G) \le \sqrt{2d(d-\lambda_2)} \quad \lambda_1 = d \le \lambda_2 \le ... \le \lambda_N$

то для минимизации h нужно брать вторую по величине компоненту спектра наиболее близкой к наибольшей. Это условие как раз хорошо выполняется в графах Рамануджана.

Существует множество семейств графов Рамануджана. Самое распространенное из них - семейство Любоцкого-Филипса-Сарнака - используется в основе детерминированных алгоритмов генерации графов Рамаджуана. Подробнее смотрите тут. Также существует простой для понимания и реализации алгоритм, основанный на случайном выборе регулярного графа, т.к. графы Рамануджана по своим свойствам приближены к ним. Описание алгоритма приведено ниже:

Сгенерировать случайный регулярный граф с заданным числом вершин.
Проверить граф на связность. Если он не связен, перейти к п.1.
Вычислить второе спектральное значение графа и сравнить с определением. Если не выполняется - перейти к п.1.
Ниже приведен пример сгенерированного таким образом графа Рамануджана:

Randomly-generated 3-regular Ramanujan graph with N = 16 vertices

(ссыкла на источник)

О графе состояний детерминированного генератора псевдослучайных чисел

Генератор псевдослучайных чисел (ГПСЧ) - устройство, которое в зависимости от начального состояния, представленного числом (зерном) вычисляет новое число, при этом последовательность этих чисел близка к случайной (для простоты примем, что состояние и выходное значение - одно и то же, однако в общем случае это не так). Одним из критериев качества ГПСЧ является число периодов (чем меньше, тем лучше) и их длина (чем длиннее, тем лучше). Генератор является частным случаем клеточного автомата, который, как описано выше, может быть представлен в виде графа (вершины будут обозначать не ячейки памяти, а состояния).

Рассмотрим пример. Пусть с помощью ГПСЧ была получена последовательность чисел: {1, 5, 3, 3, 2, 4, 6, 2, 0, 4}. Тогда граф состояний будет выглядеть следующим образом:

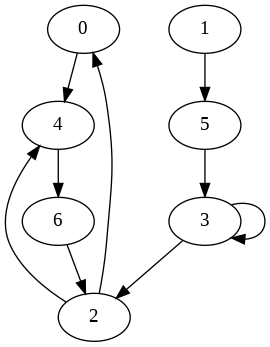
Рассмотрим более практичный пример. Пусть дан простой детерминированный ГПСЧ, у которого каждое состояние имеет один образ (линейно конгруэнтный генератор, генератор на регистре сдвига, и др.). Пусть этих состояний всего 10 (от 0 до 9 включительно). При тестировании устройства была получена очень длинная последовательность псевдослучайных чисел, и после ее обработки построили граф состояний:

Видно, что данный генератор отнюдь не идеальный: при максимальном периоде 10 на графе можно найти циклы длиной 5, 3 и даже 1. Граф самого безопасного ГПСЧ на десяти состояних должен был бы выглядеть так:

Граф состояний детерминированного ГПСЧ с максимально возможным периодом

Очевидно, что на практике число состояний детерминированного ГПСЧ делают очень большим. Это увеличивает вероятность того, что средняя длина цикла велика. В хороших ГПСЧ она достигает трехзначной степени двойки. Наличие циклов меньшей длины ухудшает его качество, т.к. может привести к полной детерминированности маленького и замкнутого множества состояний. Циклы в графе можно искать c помощью поиска в глубину с отслеживанием ранее проиндексированных вершин.

Заключение

Таким образом, в данной статье были рассмотрены базовые понятия и алгоритмы из теории графов, имеющие практическое применении в криптографии. Освещены такие понятия, как NP-полнота, нулевое разглашение и др. Приведено множество иллюстративных примеров (граф Рамануджана, ГПСЧ на регистре сдвига) и реализаций алгоритмов с ссылками на источники. Надеюсь, что данная статья будет полезной для любопытных читателей.

Tags:

Hubs: