Comments 10
Я бы немного усовершенстовал алгоритм. Если вы хотите добиться действительно случайного выбора точки и маскимально равномерного распределения.
Ибо сейчас выбор точки вовсе не случайный как минимум потому что площади треугольников разные. А вы выбираете их случайно с одинаковой вероятностью. На треуголниках более менее одинакового размера не очень заметно. Но даже на вашем скрине видно, что маленькие заполненны сильнее.
Нужно сделать, чтобы вероятность была взвешена относительно площади треугольника, то бишь равна площади треугольника деленной на площадь всей фигуры.
Ну и по поводу генерации случайной точки внутри самого треугольника, я бы тоже немного подумал. Для равносторонних треугольников ваш аглоритм возможно работает исправно. Но здесь вы опять же не учитываете разные длины сторон треугольника, при этом выбирая их с одинаковой вероятностью. На скрине это тоже заметно немного, что есть четкие зоны с большей и меньшей плотностью распределения
Спасибо за комментарий, я учту ваши замечания для улучшения алгоритма поиска!
Если Вы хотите помочь в модернизации работы программы, то исходный код открыт на GitHub
Для равносторонних треугольников ваш аглоритм возможно работает исправно
Даже для них - не совсем. Как я понимаю, выбор точки на стороне треугольника (п.3) и выбор точки на отрезке между п.3 и центром масс (точка О) делается с равномерной вероятностью по отрезку. Соответственно, приоритет будет у точек, которые лежат вблизи перпендикуляра от т.О до стороны (он самый короткий из отрезков), и разумеется у точек вблизи т.О.
На самом деле, не надо здесь точку О. Пусть у нас треугольник АВС, то просто берем случайную точку М на стороне ВС, потом случайную точку на отрезке АМ. И остается смекнуть такие функции распределения вероятностей на отрезках ВС и АМ, чтобы вышеописанных проблем не было.
если мы выбираем центр треугольника, из него пускаем случайный луч, и на этом луче случайно ставим точку- перпендикуляры к сторонам короткие, а лучи, идущие в углы- длинные, и на этих лучах плотность точек будет разная, вне зависимости от равносторонности или равнобедренности треугольников. Равномерное распределение точек по треугольнику можно получить примерно так: пусть треугольник задан точками А1, А2, А3.
возьмем два базисных вектора
b1=А2-А1 и b2=А3-А1.
возьмем два весовых коэффициента
k1=Rand(1.0) и k2=Rand(1.0);
Если k1+k2<1.0
построим точку Р= A1 + k1*b1+k2*b2,
иначе- построим точку P= A1+ (1-k1)*b1+(1-k2)*b2.
векторы b1 b2 задают параллелограмм A1,A2,A2+A3-A1,A3.
k1*b1+k2*b2- случайная точка в этом параллелограмме с равномерным распределением. k1+k2>1- условие того, что эта точка находится в этом параллелограмме за диагональю A2-A3. В этом случае мы отражаем эту точку относительно диагонали А2-А3, возвращая ее в требуемый нам треугольник и сохраняя равномерное распределение точек.. А если k1+k2<1- то точка сразу попала в исходный треугольник, и ничего делать не надо. И все это почти минимумом операций.
И обязательно надо выбирать вероятность попадания в треугольник не согласно его порядковому номеру, а по площади. То есть, каждому треугольнику присваиваем вес
S_summ = Summ(TriangleArea)
w[k]= Triangle[k].Area/S_summ;
а потом для поиска нового случайного треугольника делаем что-то типа такого:
r= Rand(1.0)
k=0
while (r>w[k]) {
r -= w[k]
k++
}
return k
Вам, судя по задаче, производительность расчетов не суть как важна, да и на равномерность распределения точек по полигону Вам тоже, видимо, можно закрыть глаза, если бы все треугольники были примерно близкой площади. Но лучше все-таки использовать аккуратные алгоритмы. А вот если в триангуляции вдруг вылезет область, где будет много мелких треугольников- то тогда Ваши коты будут тереться именно в ней, изредка выбегая в большие треугольники, и это будет заметно.
Я решал похожую задачу для неровных поверхностей чуть по другому, с помощью ускоряющей структуры.
Задача легко разбивается на 2 - выбор случайного треугольника и выбор случайной точки на нем.
Первую задачу для некоторых случаев можно решать наивно - выбрать просто случайный треугольник. Это будет работать плохо, если в меше есть треугольники с очень разной площадью. Второй вариант - найти площади всех треугольников, просуммированный вариант сложить в сортированный массив и выбирать бинарным поиском.
Найти случайную точку на треугольнике достаточно легко - находим такую в квадрате с размером 1 (случайный X/Y), потом те точки, для которых x + y > 1 разворачиваем (умножаем на -1), а потом X умножаем на вектор AB целевого треугольника, а Y - на AC и складываем.

Да, естественно алгоритм исходил из того, что тесселяцию искать не нужно - у нас ведь есть данные меша, который отправляется в коллайдер.
Ускоряющая структура соответственно состояла из массива, который содержал суммы площадей треугольников для поиска взвешенного случайного и вектора AB/AC для поиска точки
Про равномерное распеделение точек были статьи, например этот перевод https://habr.com/ru/post/440316/.
Я первое что подумал это поискать про вычисление площади треугольника (полигонов) методом Монте-Карло.
Площадь треугольника вычисляется за пару сложений и умножений, зачем Монте-Карло? Если точек много, то целесообразно после триангулизации посчитать площади каждого треугольника, затем, зная нужное количество точек вычислить сколько точек для каждого треуголника (пропорционально площади), и наконец, сгенерировать в каждом треугольнике нужное количество случайных точек. Все. Задача для школьников.
Если уж вы всё равно делаете триангуляцию, легко допилить алгоритм чтобы он выдавал действительно равномерно распределенные точки.
Сначала выбираете треугольник в котором будет лежать конечная точка, вероятность выбора треугольника пропорциональна его площади. Можно использовать, например, reservoir sampling.
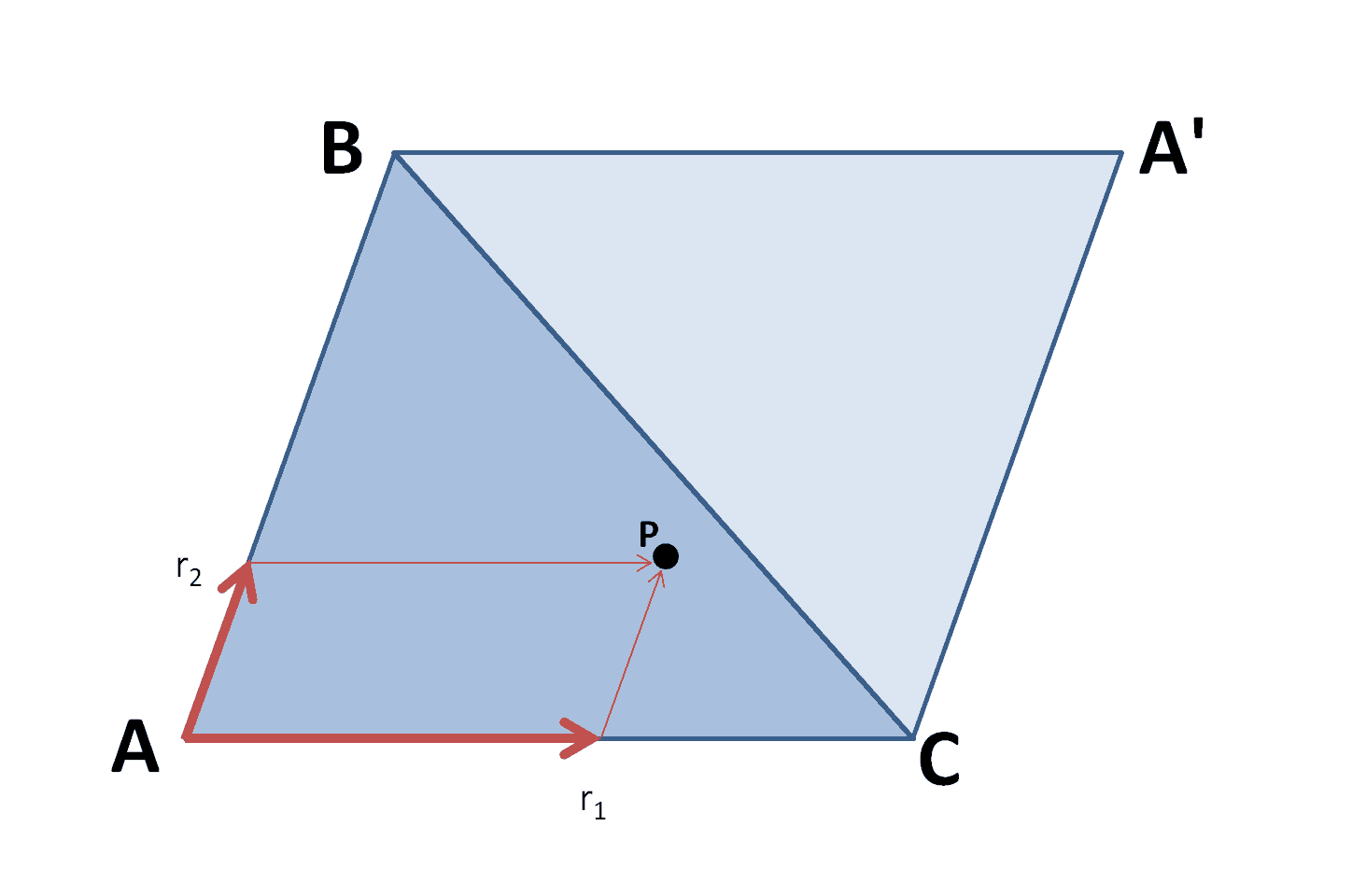
После этого выбираете случайную точку в треугольнике. Ваш метод, к сожалению, выдаёт неравномерное распределение что видно даже в вашем примере с 10к точек. Лёгкий способ — в уме дополнить треугольник до параллелограма как на картинке ниже. Становится очевидным что можно выбрать случайную точку в единичном квадрате, если она попала в верхний треугольник — отразить относительно центра, а потом перемапить базисные вектора с (0, 1), (1, 0) на AB, AC.
Поиск случайной точки на PolygonCollider2D Unity