LC ladder component values can have different values for the same transfer function. Published tables have only one set. Why?
Computing LC ladders
If we write a transfer function of an LC ladder, we find that the same result can be achieved using different LC values.
Short example for a 2nd order series LC ladder with parameters:
a cutoff frequency is 1 rad (0.159 Hz), quality factor is 0.636 (Bessel), source is 1 Ohm, termination is 1 Ohm.
The transfer function is:
A
H(s) = —————————————————————
(1 + s/(Q ω) + s²/ω²)
Rt 1
H(s) = ——————— ———————————————————————————————————————————————————————
Rs + Rt 1 + s (L + C Rs Rt) / (Rs + Rt) + s² L C Rt / (Rs + Rt)Solving the equations using a math software, obtain the values:
L = 0.885 H, C = 2.26 F
L = 2.26 H, C = 0.885 F
The transfer functions match.
Also, for higher order ladders several solutions can be found.
For high frequency circuits input impedance of a ladder is important. One of known ways to compute LC ladder values to match impedances is:
Compute poles of a transfer function.
Compute a polynomial from the poles to get H(s).
Compute product of reflection functions p(s)*p(-s).
Find input reflection p(s).
Compute input impedance Zin from p(s).
Compute ladder component values by continued fraction expansion.
The most complex part is extracting p(s) from p(s)*p(-s).
Books say that to find it, zeroes of the p(s)*p(-s) polynomial should be computed. They also say that there are no restrictions for used zero group positions. They also say that a ladder structure is defined by numerator and denominator orders.
Comparison of results
Let’s compute variants for 5th order Butterworth LC ladder. A cutoff frequency is 1 rad (0.159 Hz) and to make it more interesting, a source is 1 Ohm, a termination is 10 Ohm.
The roots of the numerator of p(s)*p(-s) in this case:
-0.9607 + 0i, +0.9607 + 0i
-0.7772 + 0.5647i, -0.7772 - 0.5647i
+0.7772 + 0.5647i, +0.7772 - 0.5647i
-0.2969 + 0.9136i, -0.2969 - 0.9136i
+0.2969 + 0.9136i, +0.2969 - 0.9136iThere are 3 groups of the roots:

7 different solutions with positive values were found with the same polynomial orders:
Zin 2.0 s^5 + 6.345 s^4 + 10.07 s^3 + 9.878 s^2 + 5.992 s + 1.818
——————— = —————————————————————————————————————————————————————————————
Rsource 0.1273 s^4 + 0.4039 s^3 + 0.594 s^2 + 0.48 s + 0.1818
Z1 = 15.71, Z2 = 0.1727, Z3 = 14.09, Z4 = 0.0912, Z5 = 3.152
Zin 2.0 s^5 + 4.424 s^4 + 5.941 s^3 + 4.559 s^2 + 2.183 s + 0.1818
——————— = ——————————————————————————————————————————————————————————————
Rsource 2.049 s^4 + 4.531 s^3 + 5.913 s^2 + 4.289 s+ 1.818
Z1 = 0.976, Z2 = 12.19, Z3 = 0.1794, Z4 = 11.4, Z5 = 0.0452
Zin 2.0 s^5 + 3.236 s^4 + 5.236 s^3 + 5.236 s^2 + 3.236 s + 1.818
——————— = —————————————————————————————————————————————————————————————
Rsource 3.236 s^4 + 5.236 s^3 + 5.236 s^2 + 3.236 s + 0.1818
Z1 = 0.618, Z2 = 1.618, Z3 = 11.0, Z4 = 0.1618, Z5 = 6.18
Zin 2.0 s^5 + 1.315 s^4 + 7.082 s^3 + 3.463 s^2 + 4.94 s + 0.1818
——————— = —————————————————————————————————————————————————————————————
Rsource 5.157 s^4 + 3.39 s^3 + 7.01 s^2 + 1.533 s + 1.818
Z1 = 0.3878, Z2 = 1.182, Z3 = 2.177, Z4 = 7.248, Z5 = 0.1521
Zin 2.0 s^5 + 5.157 s^4 + 7.082 s^3 + 7.01 s^2 + 4.939 s + 1.818
——————— = ————————————————————————————————————————————————————————————
Rsource 1.315 s^4 + 3.39 s^3 + 3.463 s^2 + 1.533 s + 0.1818
Z1 = 1.521, Z2 = 0.7248, Z3 = 21.77, Z4 = 0.1182, Z5 = 3.878
Zin 2.0 s^5 + 2.048 s^4 + 5.941 s^3 + 5.913 s^2 + 2.183 s + 1.818
——————— = —————————————————————————————————————————————————————————————
Rsource 4.424 s^4 + 4.531 s^3 + 4.559 s^2 + 4.289 s + 0.1818
Z1 = 0.4521, Z2 = 1.14, Z3 = 1.794, Z4 = 1.219, Z5 = 9.763
Zin 2.0 s^5 + 0.1273 s^4 + 10.07 s^3 + 0.594 s^2 + 5.992 s + 0.1818
——————— = ———————————————————————————————————————————————————————————————
Rsource 6.345 s^4 + 0.404 s^3 + 9.878 s^2 + 0.48 s + 1.818
Z1 = 0.3152, Z2 = 0.9123, Z3 = 1.409, Z4 = 1.727, Z5 = 1.571Use a simulator to verify the results.
Since all the polynomials have numerator orders higher than their denominator, they all should work in series structure. But it is not!
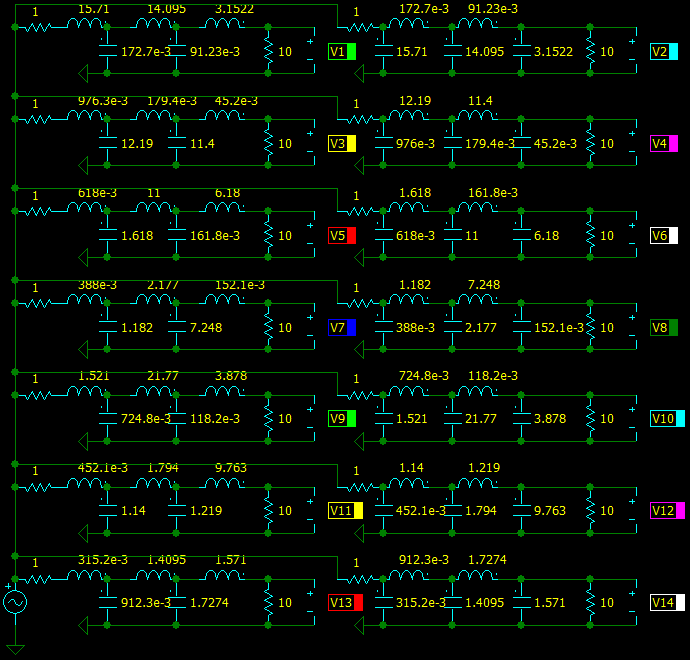
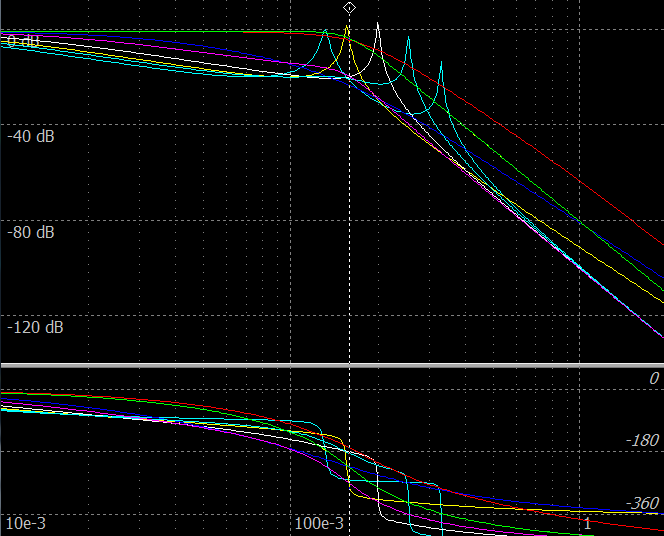
Frequency responses match for sets 1, 3, 5, 6 in series structure and 2, 4, 7 in shunt structure. There must be some other sign of the structure.
Now compare their input impedances. Amplitude shows impedance module. 0 dB is 1 Ohm in the chart, +20 dB is 10 Ohm. Phase shows image part of a value. 0 degrees means that impedance is real.
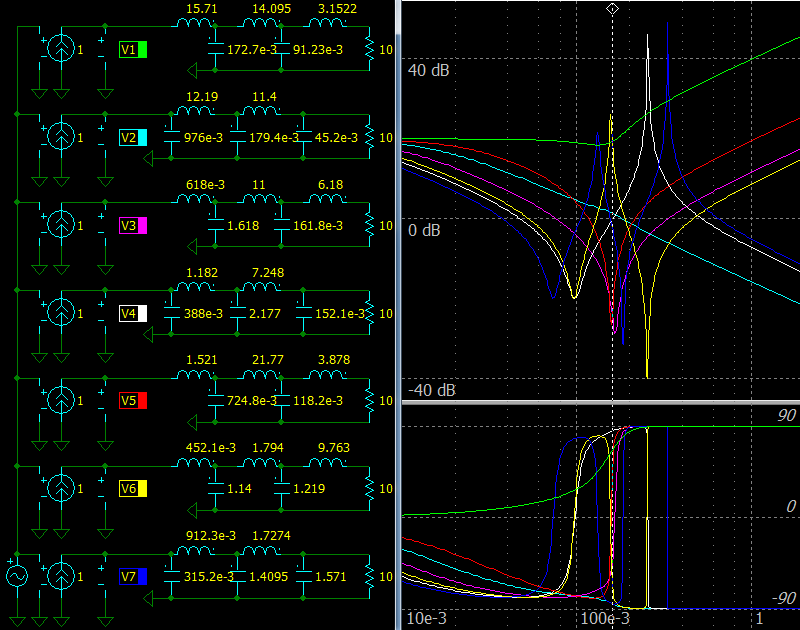
Only 1st circuit has input impedance closest to a real value (green lines) in the pass-band. It is the values which can be found in tables in books. Now it is clear why.
The values of the 1st circuit are computed using only left half plane zeroes of the p(s)*p(-s).
Conclusion
LC ladders with the same transfer functions can be built using different component values. There is no big difference if it is a low frequency circuit. For high frequency circuits input impedance is important. Use either values from tables or compute them using only left half plane zeroes of a p(s)*p(-s).
Unfortunately, some books have tables with typos. Use [1].
Verify what you read.
There are no solutions for even-order Chebyshev filters when a source is equal to termination. The higher ripple the higher a termination to source ratio should be to get a solution. Some tools compute ladder values using iterative equations [2] and can compute values at any source and termination for even-order Chebyshev filters. Be careful with such tools. [3] offers a way to find solutions for band-pass filters.
If you are interested to see a code for old computers, see [4].
References
Anatol I. Zverev, “Handbook of Filter Synthesis”.
Lars Wanhammar, “Analog Filters Using MATLAB”.
Songbai Zhang, Lei Zhu, “General synthesis method for symmetrical even-order Chebyshev bandpass filter”.
Thomtavanit Hatayodom, “Ladder network transfer function characteristics”. Link.
"idealCircuit", a simulator. Link.
Nuhertz, Filter Solutions. Link.
"Circuit Calculator", an electronics circuit design tool. Link.