Здравствуйте, на Хабре уже была статья Indalo, посвященная AdaBoost, точнее, некоторому его применению. Я же хочу более детально остановиться на самом алгоритме, заглянуть в его реализацию и продемонстрировать его работу на примере моей программы.
Итак, в чем же заключается суть методики Adaboost?
Суть заключается в том, что если у нас есть набор эталонных объектов (точки на плоскости), т.е. есть значения и класс, к которому они принадлежат (например, -1 – красная точка, +1 – синяя точка), кроме того имеется множество простых классификаторов (набор вертикальных или горизонтальных прямых, которые разделяют плоскость на две части с наименьшей ошибкой), то мы можем составить один лучший классификатор. При этом в процессе составления или обучения финального классификатора акцент делается на эталоны, которые распознаются «хуже», в этом и заключается адаптивность алгоритма, в процессе обучения он подстраивается под наиболее «сложные» объекты.
Псевдокод алгоритма хорошо описан на Вики. Приведем его здесь.
Дано: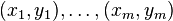 , где
, где 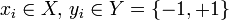 .
.
Инициализируем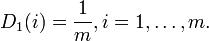
Для каждого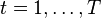 :
:
* Находим классификатор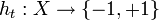 , который минимизирует взвешенную ошибку классификации:
, который минимизирует взвешенную ошибку классификации:
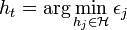 , где
, где 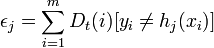
* Если величина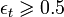 , то останавливаемся.
, то останавливаемся.
* Выбираем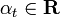 , обычно
, обычно 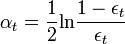 , где ?t взвешенная ошибка классификатора ht.
, где ?t взвешенная ошибка классификатора ht.
* Обновляем:
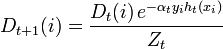 ,
,
где Zt является нормализующим параметром (выбранным так, чтобы Dt + 1 являлось распределением вероятностей, то есть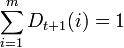 ).
).
Строим результирующий классификатор:
 .
.
Далее будем придерживаться его в наших объяснениях.
Итак, простой классификатор. Как я уже говорил, это вертикальная или горизонтальная прямая, которая разделяет плоскость на две части, минимизируя ошибку классификации: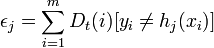 (квадратные скобки от булевого выражения равны 1, ели true, и 0, если false). На языке С# процедуру такого обучения можно написать следующим образом:
(квадратные скобки от булевого выражения равны 1, ели true, и 0, если false). На языке С# процедуру такого обучения можно написать следующим образом:
//Обучение простого классификатора
Если Вы заметили, то процедура обучения простого классификатора написана таким образом, что если ему передать веса, которые получаются на протяжении работы алгоритма AdaBoost, то тогда будет искаться тот классификатор, который минимизирует взвешенную ошибку классификации п.1. Тогда сам алгоритм на С# будет выглядеть следующим образом:
//Обучение с помощью AdaBoost
Таким образом, после выбора оптимального классификатора h_{t} \, для распределения D_i, объекты x_{i} \,, которые классификатор h_{t} \, идентифицирует корректно, имеют веса меньшие, чем те, которые идентифицируются некорректно. Следовательно, когда алгоритм тестирует классификаторы на распределении D_{t+1}, он будет выбирать классификатор, который лучше идентифицирует объекты, неверно распознаваемые предыдущим классификатором.
В случае классификации таких данных:

классифицированый рисунок с помощю AdaBoost будет выглядеть так:

Для сравнения можно привести простой алгоритм, который для каждой точки определяет ее ближайшего соседа, класс которого известен. (Понятно, что затраты такого алгоритма очень велики.)

Как видим, алгоритм, построенный с помощью AdaBoost, классифицирует намного лучше, чем один классификатор, но и он имеет ошибки. Но простота и изящность алгоритма позволила ему войти в Top 10 algorithms in data mining. Надеюсь, код, приведенный в статье, помог вам разобраться с этим алгоритмом.
Полноценный исходник программы и саму программу можно скачать здесь.
P.S. Как продолжение статьи можно расмотреть тот случай, когда общий классификатор строится не как линейная функция слабых классификаторов, а, например, квадратичная. Авторы статьи утверждают, что нашли способ, как эффективно обучать в этом случае квадратичную функцию. Или же в продолжение статьи можно рассмотреть случай, когда классов объектов больше двух.
Итак, в чем же заключается суть методики Adaboost?
Суть заключается в том, что если у нас есть набор эталонных объектов (точки на плоскости), т.е. есть значения и класс, к которому они принадлежат (например, -1 – красная точка, +1 – синяя точка), кроме того имеется множество простых классификаторов (набор вертикальных или горизонтальных прямых, которые разделяют плоскость на две части с наименьшей ошибкой), то мы можем составить один лучший классификатор. При этом в процессе составления или обучения финального классификатора акцент делается на эталоны, которые распознаются «хуже», в этом и заключается адаптивность алгоритма, в процессе обучения он подстраивается под наиболее «сложные» объекты.
Псевдокод алгоритма хорошо описан на Вики. Приведем его здесь.
Псевдокод
Дано:
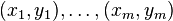 , где
, где 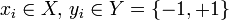 .
.Инициализируем
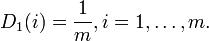
Для каждого
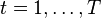 :
:* Находим классификатор
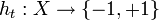 , который минимизирует взвешенную ошибку классификации:
, который минимизирует взвешенную ошибку классификации: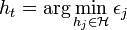 , где
, где 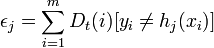
* Если величина
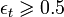 , то останавливаемся.
, то останавливаемся.* Выбираем
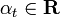 , обычно
, обычно 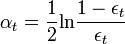 , где ?t взвешенная ошибка классификатора ht.
, где ?t взвешенная ошибка классификатора ht.* Обновляем:
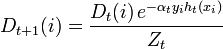 ,
,где Zt является нормализующим параметром (выбранным так, чтобы Dt + 1 являлось распределением вероятностей, то есть
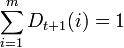 ).
).Строим результирующий классификатор:
 .
.Далее будем придерживаться его в наших объяснениях.
Простой классификатор
Итак, простой классификатор. Как я уже говорил, это вертикальная или горизонтальная прямая, которая разделяет плоскость на две части, минимизируя ошибку классификации:
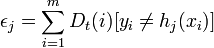 (квадратные скобки от булевого выражения равны 1, ели true, и 0, если false). На языке С# процедуру такого обучения можно написать следующим образом:
(квадратные скобки от булевого выражения равны 1, ели true, и 0, если false). На языке С# процедуру такого обучения можно написать следующим образом://Обучение простого классификатора
public override void Train(LabeledDataSet<double> trainingSet)
{
// Инициализируем наши коэффициенты D_i
if (_weights == null)
{
_weights = new double[trainingSet.Count];
for (int i = 0; i < trainingSet.Count; i++)
_weights[i] = 1.0 / trainingSet.Count;
}
Random rnd = new Random();
double minimumError = double.PositiveInfinity;
_d = -1;
_threshold = double.NaN;
_sign = 0;
// Цикл по всем координатам пространства
for (int d = 0; d < trainingSet.Dimensionality; d++)
{
// Для оптимизации в случае, если пространство огромной размерности
if (rnd.NextDouble() < _randomize)
continue;
// Сортируем данные для эффективного поиска прямой x_d = threshold
double[] data = new double[trainingSet.Count];
int[] indices = new int[trainingSet.Count];
for (int i = 0; i < trainingSet.Count; i++)
{
data[i] = trainingSet.Data[i][d];
indices[i] = i;
}
Array.Sort(data, indices);
// Определяем максимальную ошибку
double totalError = 0.0;
for (int i = 0; i < trainingSet.Count; i++)
totalError += _weights[i];
// Инициализируем значение ошибки для поиска минимальной ошибки
double currentError = 0.0;
for (int i = 0; i < trainingSet.Count; i++)
currentError += trainingSet.Labels[i] == -1 ? _weights[i] : 0.0;
// Ищем в отсортированном массиве лучший параметр threshold, который будет минимизировать
//ошибку, и определяем знак классификатора
for (int i = 0; i < trainingSet.Count - 1; i++)
{
// Обновляем ошибку при рассмотрении текущего объекта
int index = indices[i];
if (trainingSet.Labels[index] == +1)
currentError += _weights[index];
else
currentError -= _weights[index];
// Если идут одинаковые данные, то порог не ищем
if (data[i] == data[i + 1])
continue;
// Определяем потенциально возможное значение для threshold
double testThreshold = (data[i] + data[i + 1]) / 2.0;
// Запоминаем значение threshold, если ошибка минимальна, и определяем знак
if (currentError < minimumError) // Классификатор с _sign = +1
{
minimumError = currentError;
_d = d;
_threshold = testThreshold;
_sign = +1;
}
if ((totalError - currentError) < minimumError) // Классификатор с _sign = -1
{
minimumError = (totalError - currentError);
_d = d;
_threshold = testThreshold;
_sign = -1;
}
}
}
}Если Вы заметили, то процедура обучения простого классификатора написана таким образом, что если ему передать веса, которые получаются на протяжении работы алгоритма AdaBoost, то тогда будет искаться тот классификатор, который минимизирует взвешенную ошибку классификации п.1. Тогда сам алгоритм на С# будет выглядеть следующим образом:
«Сложный» классификатор
//Обучение с помощью AdaBoost
public override void Train(LabeledDataSet<double> trainingSet)
{
// Инициализируем веса D_i
if (_weights == null)
{
_weights = new double[trainingSet.Count];
for (int i = 0; i < trainingSet.Count; i++)
_weights[i] = 1.0 / trainingSet.Count;
}
// Делаем непосредственно обучение простых классификаторов
for (int t = _h.Count; t < _numberOfRounds; t++)
{
// Создаем простой классификатор и обучаем его
WeakLearner h = _factory();
h.Weights = _weights;
h.Train(trainingSet);
//Вычисляем ввзвешенную ошибку классификации
int[] hClassification = new int[trainingSet.Count];
double epsilon = 0.0;
for (int i = 0; i < trainingSet.Count; i++)
{
hClassification[i] = h.Classify(trainingSet.Data[i]);
epsilon += hClassification[i] != trainingSet.Labels[i] ? _weights[i] : 0.0;
}
// Если величина epsilon >= 0.5, то останавливаемся
if (epsilon >= 0.5)
break;
// Выбираем \alpha_{t}
double alpha = 0.5 * Math.Log((1 - epsilon) / epsilon);
// Обновляем коэффициенты D_i
double weightsSum = 0.0;
for (int i = 0; i < trainingSet.Count; i++)
{
_weights[i] *= Math.Exp(-alpha * trainingSet.Labels[i] * hClassification[i]);
weightsSum += _weights[i];
}
// Нормируем полученные коэффициенты
for (int i = 0; i < trainingSet.Count; i++)
_weights[i] /= weightsSum;
// Запоминаем классификатор с найденным коэффициентом
_h.Add(h);
_alpha.Add(alpha);
// Останавливаем обучение, если ошибка равна нулю
if (epsilon == 0.0)
break;
}
}Таким образом, после выбора оптимального классификатора h_{t} \, для распределения D_i, объекты x_{i} \,, которые классификатор h_{t} \, идентифицирует корректно, имеют веса меньшие, чем те, которые идентифицируются некорректно. Следовательно, когда алгоритм тестирует классификаторы на распределении D_{t+1}, он будет выбирать классификатор, который лучше идентифицирует объекты, неверно распознаваемые предыдущим классификатором.
Пример
В случае классификации таких данных:

классифицированый рисунок с помощю AdaBoost будет выглядеть так:

Для сравнения можно привести простой алгоритм, который для каждой точки определяет ее ближайшего соседа, класс которого известен. (Понятно, что затраты такого алгоритма очень велики.)

Заключение
Как видим, алгоритм, построенный с помощью AdaBoost, классифицирует намного лучше, чем один классификатор, но и он имеет ошибки. Но простота и изящность алгоритма позволила ему войти в Top 10 algorithms in data mining. Надеюсь, код, приведенный в статье, помог вам разобраться с этим алгоритмом.
Полноценный исходник программы и саму программу можно скачать здесь.
P.S. Как продолжение статьи можно расмотреть тот случай, когда общий классификатор строится не как линейная функция слабых классификаторов, а, например, квадратичная. Авторы статьи утверждают, что нашли способ, как эффективно обучать в этом случае квадратичную функцию. Или же в продолжение статьи можно рассмотреть случай, когда классов объектов больше двух.