Задача 1.3
Задача 1.4
Задача 1.5
Задача 1.6
Задача 1.7

Планиметрия изучается в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.

В данной статье приводятся альтернативные (подсказкам) решения задач из первого раздела приложения Euclidea (геометрические построения с помощью циркуля и линейки).

В данной статье рассматриваются различные варианты сортировки обменами, а также даётся описание простого графического приложения processing.js с примерами сортировок.

Пузырьковая сортировка

Простейший вариант: перебирать массив от первого элемента к последнему, меняя местами (если потребуется) соседние элементы.

→ Проверить здесь

Часть I
Часть II

В данной статье рассматривается метод оценок диапазона принимаемых значений и связь этого метода с задачами, содержащими модуль.

---

При решении некоторых задач необходимо рассматривать диапазон, в пределах которого может находиться искомая величина.

Рассмотрим метод оценок при решении неравенств.
Дать оценку сверху означает определить максимальное значение, которое может принимать искомая величина.

Предположим, что цена за одну единицу товара может колебаться в пределах от 5 до 10 RUB. Для двух единиц товара оценка сверху составляет 10+10=20 RUB, оценка снизу 5+5=10 RUB.

Рассмотрим задачу из задачника профильной направленности М.И. Башмакова
37. Известны оценки для переменных $$ и $$

Дайте оценки сверху для следующих выражений:
1. $$
2. $$

5. $$
6. $$

8. $$
9. $$

Часть I
Часть II
Часть III
Часть IV
Часть V


На данном ресурсе уже была опубликована статья, посвящённая RAM-машине
Wikipedia также содержит статью об этой вычислительной модели

RAM-машина, которая упоминается в книге «Построение и анализ вычислительных алгоритмов» (авторы: Ахо, Хопкрофт, Ульман) имеет ограниченный набор арифметических команд (сложение, вычитание, умножение, деление), команду безусловного перехода, две команды условных переходов. Здесь же из арифметических команд присутствуют только сложение и вычитание, команды ветвления (переходов) будут идентичными командам, приведённым в книге

LIttle Man Computer ссылка обладает схожим набором команд
Online симулятор LMC находится здесь

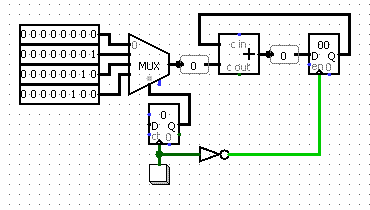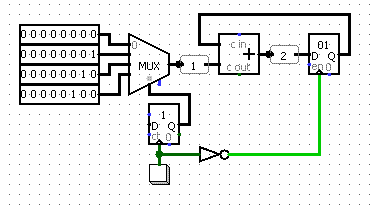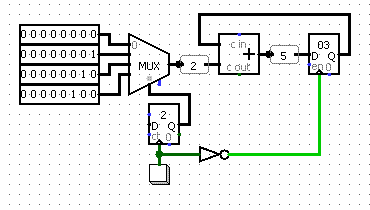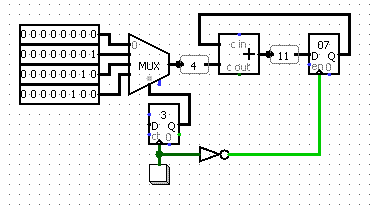
Схема АЛУ представлена ниже.
Шина соединяет память данных с сумматором (обозначен плюсом), вычитателем (обозначен минусом) и мультиплексором MUX.
Переключение между сумматором и вычитателем производится мультиплексором.
Также в мультиплексор загружаются числовые данные из устройства ввода data_input (в физическом воплощении — это набор переключателей).

Флаги состояния Acc>=0 и Acc=0, а также устройство вывода подключены к выводу аккумулятора


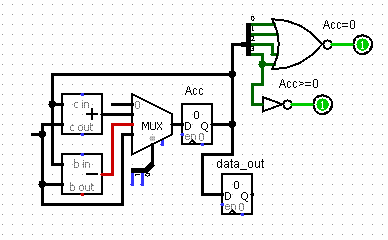
Отличием LIttle Man Computer от RAM-машины является механизм, обеспечивающий косвенную адресацию (возможность работать с числом, хранящемся в памяти, как с адресом).

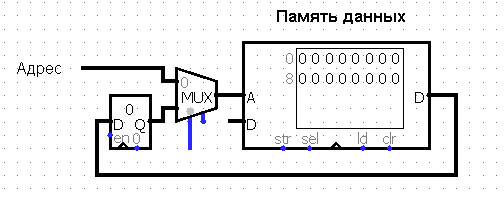
Для того, чтобы работать с числом, хранящимся в памяти, как с адресом, подключим к адресному входу Памяти Данных мультиплексор MUX, осуществляющий выборку между, собственно, адресом (поступающим из Памяти Команд) и числом, представляющем адрес и хранящемся в Памяти Данных.

Часть I
Часть II
Часть III
Часть IV
Часть V

Данная статья посвящена созданию интерпретатора некого эзотерического языка, в основе которого лежит архитектура Little Man Computer.
Фактически, это эмулятор ассемблера для LMC, только здесь вместо ассемблерных команд
INP (загрузить число в аккумулятор из устройства ввода),
STA (сохранить число из аккумулятора в память),
ADD (прибавить к числу в аккумуляторе число из памяти),
SUB (вычесть из числа в аккумуляторе число из памяти),
OUT (вывести число в аккумуляторе устройство вывода)
… используются спец-символы.
Команды переходов от ячейки к ячейке в памяти команд соответствуют командам, сдвигающим считывающую головку машины Тьюринга в языках brainfuck и P′′.
В языке bf команда + (плюс) производит замену текущего символа $$ следующим за ним (в ASCII-таблице) символом $$. Так, если на ленте Тьюринга изначально находится символ «0», то команда $$ запишет вместо него символ «1».

Эта статья о трансляторе эзотерического языка на TurboAssembler'e (TASM).
P′′ — низкоуровневый язык программирования, созданный в 1964 году Коррадо Бёмом.
Этот язык разрабатывался для реализации циклов без использования оператора GOTO.
В данной статье демонстрируется создание некого транслятора на низком уровне, в котором обработка текста программы (строки) производится посредством условных и безусловных переходов, т.е. низкоуровневых эквивалентов оператора GOTO.

Вот здесь лежит форк визуализатора(visualizer), позволяющего выполнить отладку bf-программ в пошаговом режиме

Машина, которой управляют команды транслятора, состоит из упорядоченного набора ячеек и указателя текущей ячейки, подобно тому, как организована машина Тьюринга. Кроме того, подразумевается устройство общения с внешним миром (см. команды. и ,) через поток ввода и поток вывода.

Сперва напишем транслятор на каком-нибудь высокоуровневом языке, например, на Паскале.

Пусть массив data_arr представляет память данных (ленту Тьюринга), пусть строка str_arr содержит команды.

Напишем программу, выводящую символ, ascii-код которого соответствует количеству + (поэтому нам нужны будут только команды + и .)

var
 data_arr:array[1..10] of integer;    // массив данных
 str_arr: string;                     // команды  
 i, j: integer;                       // индексы строки и массива
begin
 j:=1;                  // нумерация элементов массива начинается с единицы
 readln(str_arr);       //считываем строку

 for i:=1 to length(str_arr) do begin    // в цикле обрабатываем строку
  if (str_arr[i]='+') then data_arr[j]:= data_arr[j]+1;
  if (str_arr[i]='.') then write(chr(data_arr[j]));
 end;
end.

bf-код +++++++++++++++++++++++++++++++++. выдаст ! (ascii-код символа ! равен 33 ).

Программу можно проверить в online ide ideone.com

В данной статье рассматриваются различные методы приближений иррациональных чисел, а также попутно затрагиваются вопросы, косвенно связанные с этой темой

---

В сборнике Арнольда есть следующая задача

38. Вычислить сумму:

$$

(с ошибкой не более 1% от ответа)

Ниже представлен алгоритм для вычисления частичных сумм этого ряда на языке Scheme (Lisp), который позволяет производить вычисления в обыкновенных дробях

#lang racket
(define series_sum
 ( lambda (n)
  (if (= n 0) 0
    (+ (/ 1 (* n (+ n 1))) (series_sum(- n 1)))
  ) ) )
(series_sum 10)
(series_sum 100)
(series_sum 1000)
(series_sum 10000)
(series_sum 100000)
(series_sum 1000000)

(define series_sum_1
 ( lambda (n)
  (if (= n 0) 0 
    (+ (/ 1.0 (* n (+ n 1.0))) (series_sum_1(- n 1.0)))
  ) ) )
(series_sum_1 10)
(series_sum_1 100)
(series_sum_1 1000)
(series_sum_1 10000)
(series_sum_1 100000)
(series_sum_1 1000000)

Часть I
Часть II
Часть III
Часть IV
Часть V

Это полная версия предыдущей статьи, к которой добавлены тестбенчи.

Спроектируем Little Man Computer на языке Verilog.

Статья про LMC была на Хабре.

Online симулятор этого компьютера здесь.

Напишем модуль оперативной памяти (ОЗУ), состоящий из четырех (ADDR_WIDTH=2) четырёхбитных (DATA_WIDTH=4) слов. Данные загружаются в ОЗУ из data_in по адресу adr при поступлении тактового сигнала clk.

module R0 #(parameter ADDR_WIDTH = 2, DATA_WIDTH = 4)
(
    input clk, //тактовый сигнал
    input [ADDR_WIDTH-1:0] adr, //адрес
    input [DATA_WIDTH-1:0] data_in, //порт ввода данных
    output [DATA_WIDTH-1:0] RAM_out //порт вывода данных
);
    reg [DATA_WIDTH-1:0] mem [2**ADDR_WIDTH-1:0]; //объявляем массив mem
 
    always @(posedge clk) //при поступлении тактового сигнала clk 
        mem [adr] <= data_in; //загружаем данные в ОЗУ из data_in 
    
    assign RAM_out = mem[adr]; //назначаем RAM_out портом вывода данных
endmodule

Часть I
Часть II
Часть III
Часть IV
Часть V

Спроектируем Little Man Computer на языке Verilog.

Статья про LMC была на Хабре.

Online симулятор этого компьютера здесь.

Напишем модуль оперативной памяти RAM/ОЗУ, состоящий из четырех (N=2) четырёхбитных (M=4) слов. Данные загружаются в ОЗУ из data_in по адресу adr при нажатии на кнопку:

module R0 #(parameter N = 2, M = 4)
(
input RAM_button, //кнопка
input [N-1:0] adr, //адрес
input [M-1:0] data_in, //порт ввода данных
output [M-1:0] RAM_out //порт вывода данных
);
reg [M-1:0] mem [2**N-1:0]; //объявляем массив mem
always @(posedge RAM_button) //при нажатии на кнопку
mem [adr] <= data_in; //загружаем данные в ОЗУ из data_in 
assign RAM_out = mem[adr]; //назначаем RAM_out портом вывода данных
endmodule

Это начальный вариант статьи о процессоре, конечный вариант этой же статьи здесь.

Спроектируем в Logisim'е устройство, позволяющие суммировать наборы чисел, хранящихся в памяти. Возьмем набор восьмиразрядных чисел и подключим его к мультиплексору, переход от одного числа к другому будем осуществлять с помощью счетчика, подключенного к выбирающему входу мультиплексора, а к выходу мультиплексора подключим сумматор и аккумулятор. В качестве тактового генератора будем использовать кнопку. Данные будут загружаться в аккумулятор при отпускании кнопки (это осуществляется с помощью элемента НЕ, подключенного к кнопке).

Часть I
Часть II
Часть III
Часть IV
Часть V

Одна из глав книги «Код» Чарльза Петцольда посвящена проектированию блоков CPU и в начале главы описывается устройство, позволяющие суммировать наборы чисел, хранящихся в памяти. Спроектируем похожую схему в Logisim. Возьмем набор восьмиразрядных чисел и подключим его к мультиплексору, переход от одного числа к другому будем осуществлять с помощью счетчика, подключенного к выбирающему входу мультиплексора, а к выходу мультиплексора подключим сумматор и аккумулятор. В качестве тактового генератора будем использовать кнопку. Данные будут загружаться в аккумулятор при отпускании кнопки. Это осуществляется с помощью элемента НЕ, подключенного к кнопке. Про реализацию этих функциональных блоков в виде отдельных микросхем далее в статье.

Для запуска программ, приведённых в статье, можно использовать DrRacket. Для начала рассмотрим связь конечного автомата и игрового процесса. Объект управления в игре можно представить в виде конечного автомата. Рассмотрим программу, моделирующую светофор. Этот пример был описан в предыдущей статье.

Переходом в другое устойчивое состояние является переключение сигнала светофора. Диаграмму состояний можно изобразить в следующем виде.

Следующая статья о том, как писать игры на Scheme

Учебник HtDP (How to Design Programs), посвящен программированию на языке Scheme в среде drRacket.
drRacket можно скачать с сайта.
Вводная часть учебника содержит описание функции empty-scene, предназначенной для работы с изображениями. Например, эта программа создает пустую сцену

#lang racket  
(require 2htdp/image)      ;библиотека для работы с изображениями 
(empty-scene 100 60)     ;сцена (канвас) размером 100х60 

В данной статье я хочу рассмотреть вопросы, которые могут возникнуть у человека, приступившего к изучению ассемблера, связанные с установкой различных трансляторов и трансляцией программ под Windows и Linux, а также указать ссылки на ресурсы и книги, посвященные изучению данной темы.

MASM

Используется для создания драйверов под Windows.