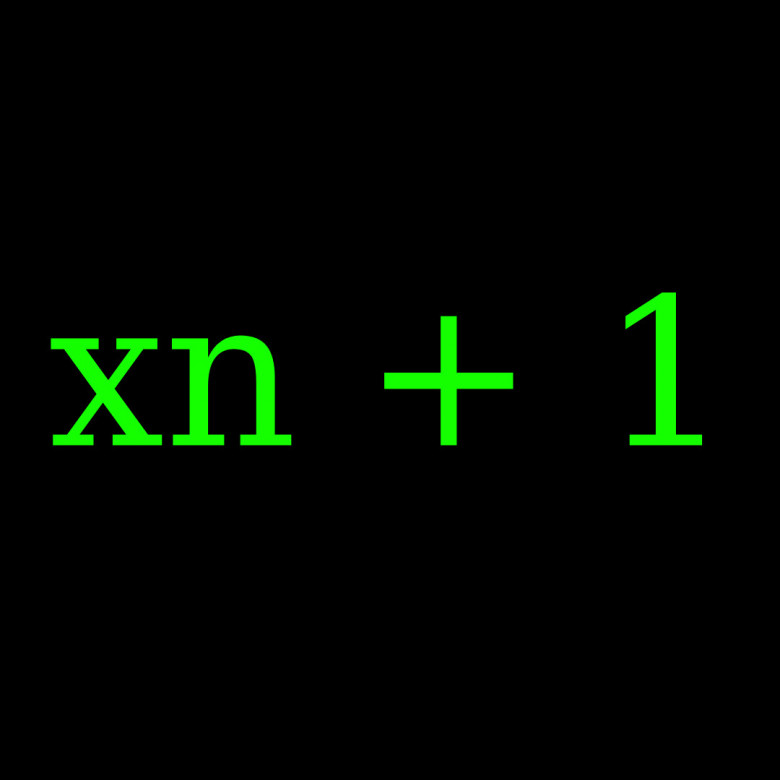
В предыдущей части мы с вами расширили всем известную гипотезу Коллатца.
Так, расширенная гипотеза Коллатца утверждает, что множество чисел , для которых есть циклы, отличные от {1}, равно {5, 181}.
Поясню другими словами..
программист
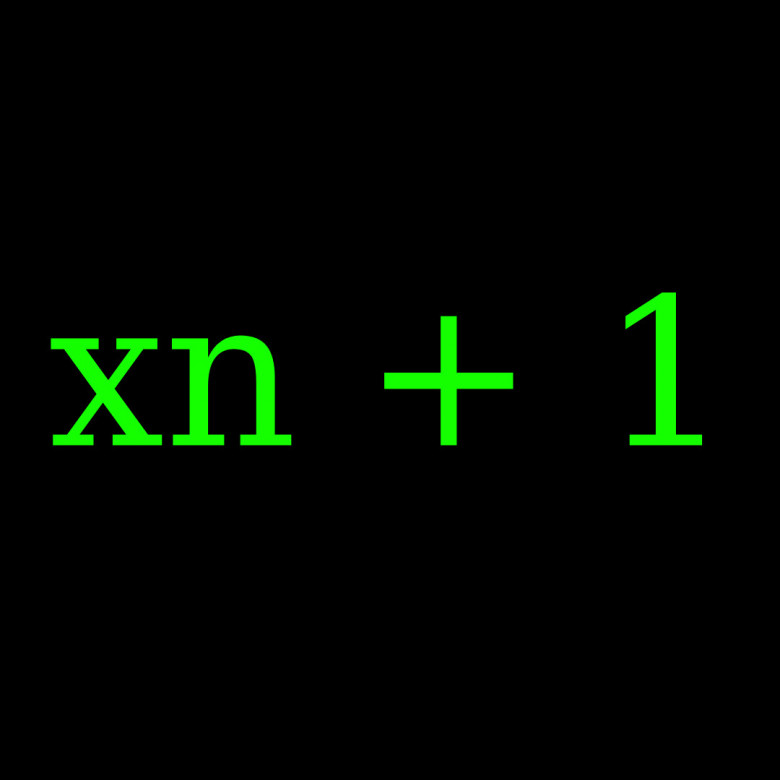
В предыдущей части мы с вами расширили всем известную гипотезу Коллатца.
Так, расширенная гипотеза Коллатца утверждает, что множество чисел , для которых есть циклы, отличные от {1}, равно {5, 181}.
Поясню другими словами..
Вероятно, все уже слышали про гипотезу "3х+1", или гипотезу Коллатца.
Правила очень простые. Берём любое число. Если оно нечётное, умножаем его на 3 и добавляем 1. Если оно чётное, делим на 2. Повторяем то же самое действие с результатом. Обязательно ли в конце мы получим 1?

Некоторое время назад, во время подготовки к интервью, я наткнулся на несколько забавных задач на сайте leetcode.com. Сами задачки не слишком сложны, но их решения довольно любопытны. Кроме того, задачки такого типа довольно часто попадаются на собеседованиях в крупных компаниях.
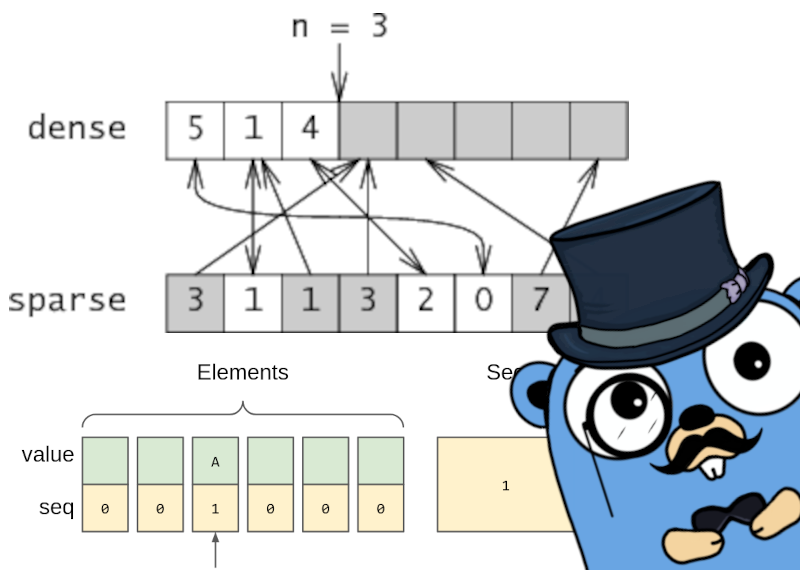
Есть такая занимательная структура данных, описанная в статье Russ Cox — sparse map.
Она используется, например, в недрах компилятора Go. А ещё в некоторых пакетах его стандартной библиотеки.
У неё есть много интересных свойств и, чем больше я о ней думаю, тем больше применений нахожу в своих задачах. Казалось бы, всё так хорошо, что лучше быть просто не может. Однако сегодня я расскажу вам о секретной штуке, которая будет экономить ещё больше бесценных наносекунд!

Речь идет о головоломках по типу кубика Рубика (за подробностями - в первую статью серии).
Алгоритмом Бога на пазле (от англ. "puzzle" - головоломка) - это кратчайший путь от состояния А до В.
Антипод - самое запутанное состояние пазла (одно из множества).
Число Бога (далее ЧБ) - это (всё эквивалентные формулировки):

По состоянию на лето 2023, в военных комиссариатах разных регионов и даже районов одного города требования к пакету документов отличаются, запись через Госуслуги может не гарантировать прием, а без личного присутствия заявителя могут вообще не захотеть общаться. Информация ниже не является полным гайдом по снятию с учета, это шаблоны документов + рекомендации из практики.
Если вкратце, то рабочий кейс, это когда: (А) имеется основание для снятия: уже живете зарубежом полгода, либо имеется иностранный ВНЖ, (B) грамотно составлено заявление на снятие с учета и подписано вашей подписью, (C) в военкомат идет ваш представитель по доверенности, которая оформлена у российского нотариуса или в зарубежном консульстве РФ.
Ниже пояснения и документы. Делайте все красиво, грамотно, и тогда результат будет ?

Есть вот такая, вроде бы, простая задача на литкоде: Дано три числа total - сколько у вас есть денег, cost1, cost2 - цены двух товаров. Надо подсчитать, сколько всего существует различных способов купить сколько-то этих двух товаров, не выходя из бюджета (значение имеет только общее количество покупок). Иными словами, сколько существет целых неотрицательных пар (x, y), таких что x*cost1+y*cost2 <= total . Например, имея товары ценами {5, 10} и 20 денег на руках, есть 9 способов потратить деньги: 0, 5, 5+5, 5+5+5, 5+5+5+5, 10, 10+5, 10+5+5, 10+10.
Она там даже помечена как medium и вообще в одну строчку решается, но это если допускать безумно медленное решение за O(total / max(cost1, cost2)) , т.е линейное от входных чисел. А сможете ли вы решить ее сильно быстрее - за O(log(max(cost1, cost2))) ? В этом случае задачка становится вполне себе hard и требует много математики и аккуратности. Если интересно решение - добро пожаловать под кат. Буду рад любым альтернативным решениям. Может кто-то сможет додуматься до похожего решения проще.