Расчёт КПД в процессах с участием везикул и кинезина

В этой статье решим следующую задачу с МХТ 2023:
Второе начало термодинамики "нарушается" практически во всех биологических системах,цена тому— энергия в виде молекул АТФ. Рассмотрим следующую ситуацию: транспортный белок кинезин способен за счёт энергии АТФ переносить из одной везикулы в другую определённое вещество.В исходной везикуле оно находилось в быстро устанавливающемся равновесии с другим веществом.При переносе порции вещества из одной везикулы в другую равновесие реакции смещается,и в одной везикуле происходит выделение тепла,а в другой — поглощение.Возможен ли такой“холодильник”в живой клетке?Как будет зависеть его КПД от выбора реакции и концентраций веществ?Сравните КПД"биологического холодильника"с КПД домашнего холодильника(около 60%).
Мной было предложено следующее решение:
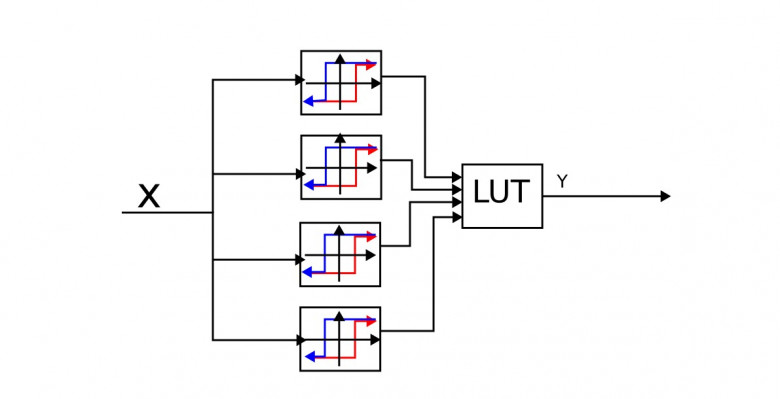
Нарисуем схему этой задачи(её физическую модель):