Просматривая различный код по выводу на экран какой-нибудь даже примитивной графики, я заметил чрезмерную любовь некоторых программистов к тригонометрии. Часто код пестрит синусами, косинусами и арктангенсами там, где без них можно обойтись. Этим грешат даже хорошие программисты, которые способны спроектировать сложную систему, но почему-то не освоили вектора в объёме школьной программы. Буквально азов векторной алгебры хватает для решения многих насущных проблем. В этом топике я хочу провести краткий ликбез, напомнить основные действия с векторами на плоскости и в качестве примера решить две задачи без тригонометрии: поиск отражённого луча по падающему лучу и произвольно расположенному зеркалу, а также рисование наконечника стрелки. Если вы можете представить в голове рисование произвольно направленной стрелки без синусов и косинусов, смело пропускайте этот топик. Для остальных постараюсь объяснять попроще.

Геометрический смысл — это отрезок на плоскости, для которого важна длина и направление, но не важно положение. То есть параллельный перенос не меняет вектора. Часто полезно отождествлять вектор с точкой (x,y) на плоскости — это всё равно что провести вектор из точки (0,0) в точку (x,y). Рассмотрим основные операции.
Сложение векторов:

Геометрический смысл изображён на картинке — мы перемещаем второй вектор, чтобы его начало совпало с концом первого, и результатом считаем вектор от начала первого до конца второго:

Умножение вектора на скаляр (число):

Геометрический смысл — удлинение вектора в соответствующее число раз, не меняя направление (разве что на противоположное, если a отрицательно). Умножение на -1 перевернёт вектор на 180°, не меняя длину. Деление вектора на число a — это умножение на 1/a.
Скалярное произведение векторов:
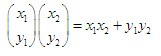
Очень важная штука. Перемножая два вектора, мы получаем число, которое характеризует длину проекции одного на другой. Перемножив два вектора, по знаку мы можем определить, направлены ли вектора в одну сторону (скалярное произведение положительно), направлены противоположно (скалярное произведение отрицательно) или перпендикулярны друг другу (произведение равно нулю). Не нужно для этого вычислять арктангенсы отношений координат каждого вектора и сравнивать углы. Два умножения, одно сложение и дело в шляпе.
Также важно, что скалярное произведение вектора самого на себя — это квадрат его длины (следствие теоремы Пифагора):
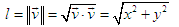
Вектор называют нормированным или единичным, если его длина равна единице. Нормировать произвольный ненулевой вектор — это поделить его на длину. Получится единичный вектор, сонаправленный исходному.
Скалярное произведение произвольного вектора на единичный даст точную длину проекции этого вектора на направление единичного. Чтобы получить не просто длину, а сам вектор-проекцию, надо умножить эту длину на наш единичный вектор:
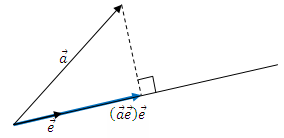
В скобках скалярное произведение векторов a и e, а затем умножение вектора e на скаляр.
Что делать, если нам нужна проекция на ненормированный вектор? Чтобы нормировать, надо извлечь корень, а это долго и грустно. Однако, если мы приглядимся к формуле, то поймём, что нам нужно поделить результат на квадрат длины, то есть просто на скалярное произведение вектора на себя. То есть проекция a на произвольный ненулевой b будет вычисляться так:

Скалярное произведение двух единичных векторов — это косинус угла между ними. Если вдруг вам всё-таки потребовался угол между направлениями, проверьте, может, вам вовсе не угол нужен, а его косинус (или синус, который в ряде случаев можно получить из основного тригонометрического тождества). Тогда вам не потребуется ковыряться с арктангенсами.
Вот, собственно, вся базовая теория. Теперь попробуем её применить.

Зная, что угол падения равен углу отражения, можно придумать какой-то такой наивный алгоритм:
Однако если мыслить векторами, то простое геометрическое построение даёт существенно более быстрое решение:
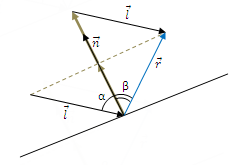
Две проекции вектора l на нормаль со знаком минус да плюс ещё один вектор l в точности дадут нам результат:
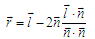
Делить не надо, если нормаль уже нормирована. Кстати, я не рассказал, как её определить. Если прямая задана двумя точками (x1,y1) и (x2,y2), то вектор нормали (ненормированый) легко определяется вот так:

Иногда важен знак нормали, чтобы знать, какая сторона прямой «внешняя». В нашей задаче это неважно, вы в этом легко можете убедиться.
Кстати, полученная формула отражённого луча действует и в трёхмерном варианте, только нормаль надо определять уже для плоскости.
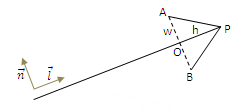
Здесь точка (x2,y2) обозначена буквой P. Необходимо вычислить координаты точек A и B, чтобы провести отрезки PA и PB. Будем считать, что нам задана продольная и поперечная длины усиков h и w. Внимательный читатель уже может сам предложить алгоритм: чтобы найти точку O, надо вычесть из P h, умноженное на единичный вектор вдоль стрелки (тут, похоже, без корня не обойтись, но он нужен всего один раз!). А затем A и B уже определяются, добавляя к O вектор нормали, домноженный на w и −w. Заметьте, что мы нигде не определяли угол раствора стрелки (вообще это арктангенс отношения w и h), но он нам и не нужен: стрелка легко рисуется и так.
Теория
Итак, вектором (рассматриваем только двумерный случай) называется пара чисел:
Геометрический смысл — это отрезок на плоскости, для которого важна длина и направление, но не важно положение. То есть параллельный перенос не меняет вектора. Часто полезно отождествлять вектор с точкой (x,y) на плоскости — это всё равно что провести вектор из точки (0,0) в точку (x,y). Рассмотрим основные операции.
Сложение векторов:

Геометрический смысл изображён на картинке — мы перемещаем второй вектор, чтобы его начало совпало с концом первого, и результатом считаем вектор от начала первого до конца второго:

Умножение вектора на скаляр (число):

Геометрический смысл — удлинение вектора в соответствующее число раз, не меняя направление (разве что на противоположное, если a отрицательно). Умножение на -1 перевернёт вектор на 180°, не меняя длину. Деление вектора на число a — это умножение на 1/a.
Скалярное произведение векторов:
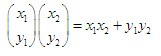
Очень важная штука. Перемножая два вектора, мы получаем число, которое характеризует длину проекции одного на другой. Перемножив два вектора, по знаку мы можем определить, направлены ли вектора в одну сторону (скалярное произведение положительно), направлены противоположно (скалярное произведение отрицательно) или перпендикулярны друг другу (произведение равно нулю). Не нужно для этого вычислять арктангенсы отношений координат каждого вектора и сравнивать углы. Два умножения, одно сложение и дело в шляпе.
Также важно, что скалярное произведение вектора самого на себя — это квадрат его длины (следствие теоремы Пифагора):
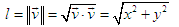
Вектор называют нормированным или единичным, если его длина равна единице. Нормировать произвольный ненулевой вектор — это поделить его на длину. Получится единичный вектор, сонаправленный исходному.
Скалярное произведение произвольного вектора на единичный даст точную длину проекции этого вектора на направление единичного. Чтобы получить не просто длину, а сам вектор-проекцию, надо умножить эту длину на наш единичный вектор:

В скобках скалярное произведение векторов a и e, а затем умножение вектора e на скаляр.
Что делать, если нам нужна проекция на ненормированный вектор? Чтобы нормировать, надо извлечь корень, а это долго и грустно. Однако, если мы приглядимся к формуле, то поймём, что нам нужно поделить результат на квадрат длины, то есть просто на скалярное произведение вектора на себя. То есть проекция a на произвольный ненулевой b будет вычисляться так:

Скалярное произведение двух единичных векторов — это косинус угла между ними. Если вдруг вам всё-таки потребовался угол между направлениями, проверьте, может, вам вовсе не угол нужен, а его косинус (или синус, который в ряде случаев можно получить из основного тригонометрического тождества). Тогда вам не потребуется ковыряться с арктангенсами.
Вот, собственно, вся базовая теория. Теперь попробуем её применить.
Вычисление отражённого луча
Отражённый луч может пригодиться не только для оптических задач, а ещё, скажем, при моделировании упругого столкновения объекта со стенкой, что незаменимо при программировании анимированных красивостей. Тогда вектор скорости объекта изменится как раз по закону отражения. Итак, у нас есть падающий вектор l и некоторая произвольная прямая, от которой производится отражение. Прямая может быть задана, к примеру, двумя точками. Требуется определить отражённый вектор r той же длины, что и l:
Зная, что угол падения равен углу отражения, можно придумать какой-то такой наивный алгоритм:
- Посчитать разность координат точек прямой, взять арктангенс их отношения — получим наклон прямой к оси x.
- Аналогично определить наклон падающего луча к оси x.
- Посчитать разность этих углов, вычесть её из 90° — получим угол падения.
- Добавить угол падения дважды и ещё 180° к углу наклона падающего луча — получим угол наклона отражённого луча.
- Вычислить длину падающего луча и умножить на синус и косинус угла наклона отражённого луча — получим результирующий вектор.
Однако если мыслить векторами, то простое геометрическое построение даёт существенно более быстрое решение:

Две проекции вектора l на нормаль со знаком минус да плюс ещё один вектор l в точности дадут нам результат:
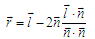
Делить не надо, если нормаль уже нормирована. Кстати, я не рассказал, как её определить. Если прямая задана двумя точками (x1,y1) и (x2,y2), то вектор нормали (ненормированый) легко определяется вот так:

Иногда важен знак нормали, чтобы знать, какая сторона прямой «внешняя». В нашей задаче это неважно, вы в этом легко можете убедиться.
Кстати, полученная формула отражённого луча действует и в трёхмерном варианте, только нормаль надо определять уже для плоскости.
Рисование стрелки
Пусть заданы концы стрелки (x1,y1) и (x2,y2). Надо нарисовать усики фиксированного размера на конце (x2,y2). Посмотрим рисунок:
Здесь точка (x2,y2) обозначена буквой P. Необходимо вычислить координаты точек A и B, чтобы провести отрезки PA и PB. Будем считать, что нам задана продольная и поперечная длины усиков h и w. Внимательный читатель уже может сам предложить алгоритм: чтобы найти точку O, надо вычесть из P h, умноженное на единичный вектор вдоль стрелки (тут, похоже, без корня не обойтись, но он нужен всего один раз!). А затем A и B уже определяются, добавляя к O вектор нормали, домноженный на w и −w. Заметьте, что мы нигде не определяли угол раствора стрелки (вообще это арктангенс отношения w и h), но он нам и не нужен: стрелка легко рисуется и так.