Comments 18
Только вот вряд ли можно назвать третий вариант генератора «цифровым»
PLL генераторы не упомянуты.
А где генерация синусоиды через решение дифференциального (разностного) уравнения на контроллере, не требующая никаких пзу?
Это по сути и есть прямой цифровой синтез, только вместо таблицы используется непосредственно вычисленные значения. Там есть про это пара строчек
Хм. Я бы сказал, что между решением разностного уравнения и использованием таблицы для последующей аппроксимации — существенная разница. И по точности, и по вычислительным затратам, и по требуемой памяти.
Вы пишете:
Вы про что конкретно говорите? Про решение разностного уравнения? Или про вычисление синуса, например, разложением в ряд?
Вы пишете:
необходим высокопроизводительный процессор, или модуль для работы с плавающей точкой. Вычисление значений в микроконтроллере может занять продолжительное время
Вы про что конкретно говорите? Про решение разностного уравнения? Или про вычисление синуса, например, разложением в ряд?
Про вычисление вцелом
Это спорное утверждение, для которого вы не привели весомых аргументов. Решение разностного уравнения, если я правильно помню, — одно умножение на константу (частоту) и одно сложение.
Уравнение будет второго порядка
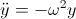
и простейшая разностная схема для него
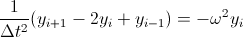
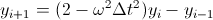
Сложность в таком методе в том, что он неустойчив — амплитуда синуса будет уходить.
Я бы предложил решать проблему «сбросом» метода раз в период например.
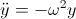
и простейшая разностная схема для него
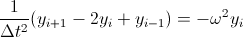
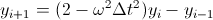
Сложность в таком методе в том, что он неустойчив — амплитуда синуса будет уходить.
Я бы предложил решать проблему «сбросом» метода раз в период например.
А если сразу писать в разностных уравнениях, минуя ненужную аппрокимацию второй производной, то получится
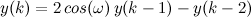 .
.
Так же, как и у вас, — умножение на константу и сложение, только константа другая.
Не совсем хорошо говорить про неустойчивость, правильнее про границу устойчивости. К насколько сильному убеганию приведет реализация с некоторой заданной точностью, да и будет ли это убегание — надо моделировать. Но с убеганием действительно можно бороться, сбрасыванием или другим образом.
В любом случае, эта реализация сильно отличается от табличной. Причем тут высокопроизводительный процессор и продолжительное время — требует пояснений.
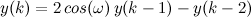 .
. Так же, как и у вас, — умножение на константу и сложение, только константа другая.
Не совсем хорошо говорить про неустойчивость, правильнее про границу устойчивости. К насколько сильному убеганию приведет реализация с некоторой заданной точностью, да и будет ли это убегание — надо моделировать. Но с убеганием действительно можно бороться, сбрасыванием или другим образом.
В любом случае, эта реализация сильно отличается от табличной. Причем тут высокопроизводительный процессор и продолжительное время — требует пояснений.
Есть ещё один способ — белый шум + цифровой фильтр. (Для читой синусоиды не очень, а для более широполосных сигналов может быть полезно). Теоретически, таким способом можно создать любой сигнал.
Вы, наверное, имели ввиду, любой гладкий? Да и то, как мне сейчас кажется, не любой сигнал, а любой желаемый спектр. Сомневаюсь, что через образующий фильтр вы сможете жестко фазу задать.
А как будут регулироваться параметры выходного сигнала? Вы предлагаете отфильтровать это дело полосовым фильтром с высокими характеристиками?
Sign up to leave a comment.
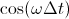 должно быть?)
должно быть?)
Виды цифровых генераторов