Comments 75
1.5 * 0.75 = 1.125 должен смочь пройти повороты (скругляя углы)
Мне кажется можно попробовать «диван набок перевернуть».
Мне кажется можно попробовать в таком направлении (извиняюсь за грубость наброска), расчётов не делал.

После поворота перевернуть :)
Задача то на плоскости, нельзя повернуть. А если рассматривать так, что можно перевернуть, то это классическая задача о перемещении дивана, тут и решать тогда нечего.
Мне кажется это очень похоже на решение, площадь должна быть близка к Pi/2

Можно увеличть площадь за счёт расширения спицы ближе к кругам. Если не пролезет — уменьшать радиусы кругов и должно пройти.
так не пролезет?
У меня появились сомнения, мне кажется эти добавки могут «зацепиться за угол»
Анализировать варианты решения — ещё больший вынос мозга, чем поиск своего :)
Похоже эта «штука» застрянет в таком положении и не пойдёт ни вперёд, ни назад.
Похоже эта «штука» застрянет в таком положении и не пойдёт ни вперёд, ни назад.
Давайте рассмотрим центр этого рисунка. Касательная к одной из линий в этой точке горизонтальна (как вы правильно изобразили). Если попытаться повернуть фигуру вокруг этой точки по часовой стрелке, мы сразу же пересечём границу канала. Можно было бы попробовать перетаскивать фигуру параллельным переносом вправо, но этого не даст сделать другая линия (касательная к которой вертикальна).
Приближает к 3/8*Pi+1/2, что порядка 1,678
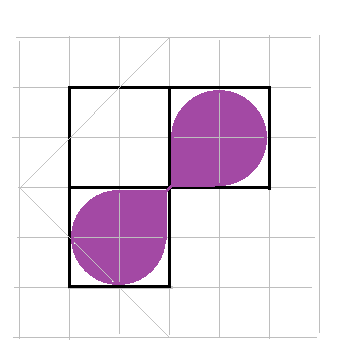
Почему приближает — место соединения не может иметь нулевую толщину, а за счёт этого надо уменьшать диаметр «капель».

Почему приближает — место соединения не может иметь нулевую толщину, а за счёт этого надо уменьшать диаметр «капель».
Мы можем считать это за нижнюю оценку или кто-то считает, что эта фигура может застрять? (Толщина соединения ненулевая, но сколь угодно малая).
Мне кажется, пройдет пилюлеобразная фигура, площадью 2,58 м^2. Длина — 1,91 м, радиус закруглений — 0,25 м.
площадь фигуры 1+1/3
рисовать ее?
рисовать ее?
Эм… 1/3 это точное число?
Если да, попробуйте нарисовать.
Если да, попробуйте нарисовать.
Да, 1+1/3 получил аналитически
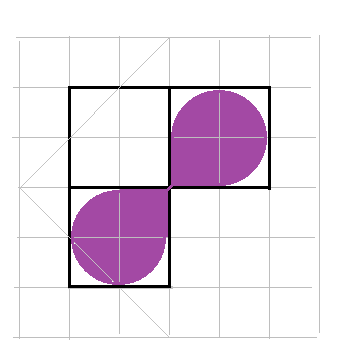
Ну вобщем суть в том что надо найти максимальное пересечение двух зеркальных треугольников со сторонами 2,2 и 2*sqrt(2).
Если обозначить cдвиг одного треугольника относительно другого за h, то площадь пересечения получается:
S = 1 — 1,5*h*h + sqrt(2)*h
Ищем максимум этой функции… Он достигается при h=sqrt(2)/3
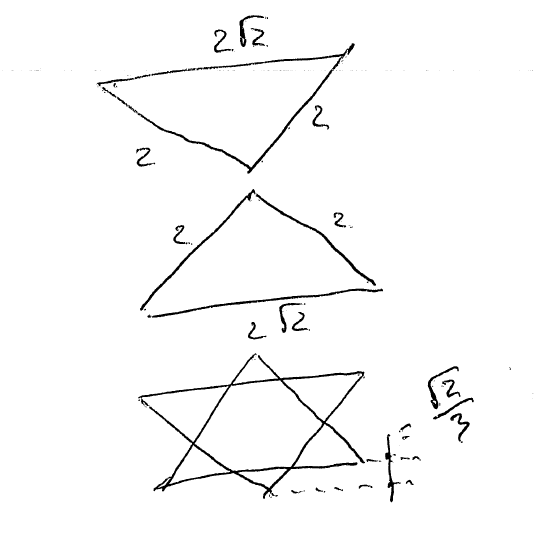
Уж извините, что рисунок не слишком гламурен ))
И, кстати, любые связи с религиозными и прочими символами тут случайны ))
Ну вобщем суть в том что надо найти максимальное пересечение двух зеркальных треугольников со сторонами 2,2 и 2*sqrt(2).
Если обозначить cдвиг одного треугольника относительно другого за h, то площадь пересечения получается:
S = 1 — 1,5*h*h + sqrt(2)*h
Ищем максимум этой функции… Он достигается при h=sqrt(2)/3

Уж извините, что рисунок не слишком гламурен ))
И, кстати, любые связи с религиозными и прочими символами тут случайны ))
Хотя… Оно должно застрять походу ))
А нее )) не должно ))
Надо бороться с ощущением, что оно туда заплывет и застрянет ровно по диагонали. Ведь, что заплывет то и выплывет ))
По сути фигура та же, что предлагал Naqq тут habrahabr.ru/blogs/zadachki/120930/#comment_4100878
Просто не надо пугаться и оставить углы острыми
Надо бороться с ощущением, что оно туда заплывет и застрянет ровно по диагонали. Ведь, что заплывет то и выплывет ))
По сути фигура та же, что предлагал Naqq тут habrahabr.ru/blogs/zadachki/120930/#comment_4100878
Просто не надо пугаться и оставить углы острыми
Приятно, что вы сами ищете ошибки в своих решениях. Это хорошая «гимнастика для ума».
Один учёный (к сожалению, забыл, кто именно), когда ему присылали доказательства теоремы Ферма, раздавал их своим студентам, а они должны были отыскать ошибку. Потом авторам «решения» отправляли ответ: «Спасибо за присланное доказательство Великой теоремы Ферма. Первая ошибка на странице… в строке ...».
Радует в этой истории то, что теорема в всё-таки была доказана :)
Один учёный (к сожалению, забыл, кто именно), когда ему присылали доказательства теоремы Ферма, раздавал их своим студентам, а они должны были отыскать ошибку. Потом авторам «решения» отправляли ответ: «Спасибо за присланное доказательство Великой теоремы Ферма. Первая ошибка на странице… в строке ...».
Радует в этой истории то, что теорема в всё-таки была доказана :)
2п/3 — sqrt(3)/2 ~ 1.228?
это был минус, парсер слишком грамотный


Да, похоже, что это и есть известное мне решение.
Только пока не публикуй рисунок.
Можешь помочь в опровержении решений с большей площадью :)
Только пока не публикуй рисунок.
Можешь помочь в опровержении решений с большей площадью :)
только НЛО теперь сможет скрыть решение…
Да, немного опоздал с коментом :)
Но всё равно пора было раскрыть интригу…
Лавры по праву достаются wirzus
Но всё равно пора было раскрыть интригу…
Лавры по праву достаются wirzus
а как быть с доказательством, что это максимум? :)
а как доказать ещё не придумал
Строгое математическое доказательство, по-видимому, вообще не существует.
Если проводить (мысленный) эксперимент и перемещать эту фигуру по каналу, мы интуитивно понимаем, что она является самой «полной», пытаясь её «нарастить», мы выйдем за границы канала.
Если проводить (мысленный) эксперимент и перемещать эту фигуру по каналу, мы интуитивно понимаем, что она является самой «полной», пытаясь её «нарастить», мы выйдем за границы канала.
Если есть задача, то есть и доказательство.
В данном случае все исходные данные есть заранее, решение, судя по всему, одно.
А значит есть и строгое доказательство.
Например, построить доказательство следующим образом:
1) Доказать, что оптимальный поворот — по окружности. Или что поворот в любом случае можно свести к повороту, когда он происходит вокруг одной очки.
2) Доказать, что эта точка — угол.
3) Доказать, что наибольшая по площади фигура, которая допускает поворот — полуокружность.
4) в связи с симметрией доказать, что поворот в другую сторону тоже ограничивается полуокружностью, но уже с центром с другой стороны.
5) Объединить решения для обоих поворотов в 1.
6) Посчитать площадь получившейся фигуры.
В данном случае все исходные данные есть заранее, решение, судя по всему, одно.
А значит есть и строгое доказательство.
Например, построить доказательство следующим образом:
1) Доказать, что оптимальный поворот — по окружности. Или что поворот в любом случае можно свести к повороту, когда он происходит вокруг одной очки.
2) Доказать, что эта точка — угол.
3) Доказать, что наибольшая по площади фигура, которая допускает поворот — полуокружность.
4) в связи с симметрией доказать, что поворот в другую сторону тоже ограничивается полуокружностью, но уже с центром с другой стороны.
5) Объединить решения для обоих поворотов в 1.
6) Посчитать площадь получившейся фигуры.
Эмм, был же вариант Laplace — Pi/2 (два круга с палочкой)?
Вариант Два круга с палочкой легко опровергается. Видно, что фигура «застряла» в таком положении. Она не может выйти и, на самом деле, никак не могла туда попасть. Невозможно указать точку, вокруг которой мы могли бы вращать фигуру, чтобы сместить её хотя бы на чуть-чуть.
А вот и не опровергается :). Вообще я имел в виду чистый вариант с палочкой (без срезов, на два коммента выше вашей ссылки), но не суть. Вариант с палочкой — чистый Pi/2. Вариант со срезами даёт большую площадь, но срезы пойдёт немного другие.
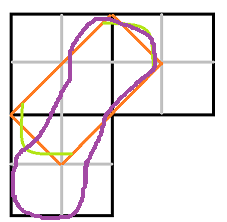
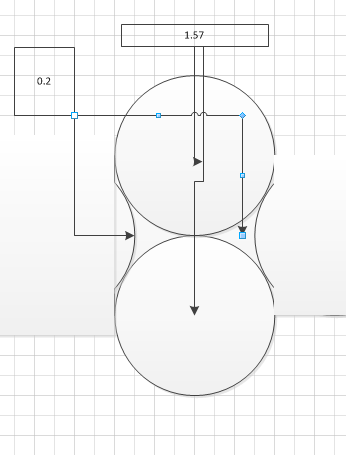
Я взял застрявший вариант lukaville и начал протаскивать его через угол. Вместе с этим я отмечал точки среза. Вот что получилось
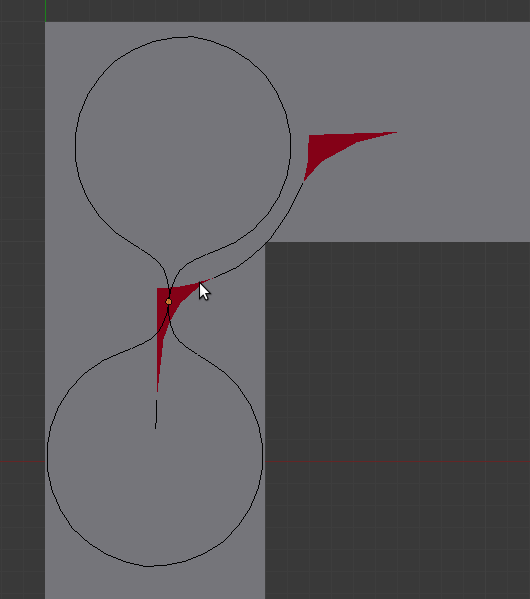
Красный объект (с курсором, лол) описывает все те точки, в которых может находится центр симметрии обрезанной фигуры. В определённый момент красный объект сливается в линию окружности радиусом sqrt(2).
Вот тот же объект на разных местах существования:

Я взял застрявший вариант lukaville и начал протаскивать его через угол. Вместе с этим я отмечал точки среза. Вот что получилось

Красный объект (с курсором, лол) описывает все те точки, в которых может находится центр симметрии обрезанной фигуры. В определённый момент красный объект сливается в линию окружности радиусом sqrt(2).
Вот тот же объект на разных местах существования:

Вы обратили внимание на этот комментарий?
«Если не пролезет — уменьшать радиусы кругов и должно пройти.» Я считаю, что существует такой эпсилон ɛ, что фигура состоящая из кругов радиуса ½-ɛ, соединённых прямоугольником толщиной в ɛ удовлетворяет условиям задачи. При этом я утверждаю, что могу уменьшать ɛ сколь угодно в сторону нуля и приближать площадь к π/2 в пределе. Я не привожу доказательства, потому что это задача очень сложна. Вы по прежнему утверждаете, что в моих рассуждениях есть очевидный изъян?
«Если не пролезет — уменьшать радиусы кругов и должно пройти.» Я считаю, что существует такой эпсилон ɛ, что фигура состоящая из кругов радиуса ½-ɛ, соединённых прямоугольником толщиной в ɛ удовлетворяет условиям задачи. При этом я утверждаю, что могу уменьшать ɛ сколь угодно в сторону нуля и приближать площадь к π/2 в пределе. Я не привожу доказательства, потому что это задача очень сложна. Вы по прежнему утверждаете, что в моих рассуждениях есть очевидный изъян?
Вообще надо бы доказать для любого эпсилона 1 > ɛ > 0, но лениво.
Вы это мне или Andrew1000000? Я говорил про картинки: вариант с простой спицей спокойно проходит без всякого уменьшения радиусов. Вариант lukaville лучше по площади, но определённо застревает.
Если вместо срезов уменьшать радиус, то в определённый момент тело пройдёт, но увеличится площадь красного участка (тело вообще будет гулять по ширине коридора, нам это надо?). Мне видится, что стоит только рассматривать случай с радиусом 0.5, с которым красный участок сходится в линию.
Всё что я сделал — практически доказал, что вариант со срезами не застревает. А вот составить аналитическое решение варианта со срезами для доказательства я не берусь, поскольку просто никогда не умел составлять уравнения дифференциально преобразованных кривых (это ведь они образуют срез? похоже на эвольвенту).
Если вместо срезов уменьшать радиус, то в определённый момент тело пройдёт, но увеличится площадь красного участка (тело вообще будет гулять по ширине коридора, нам это надо?). Мне видится, что стоит только рассматривать случай с радиусом 0.5, с которым красный участок сходится в линию.
Всё что я сделал — практически доказал, что вариант со срезами не застревает. А вот составить аналитическое решение варианта со срезами для доказательства я не берусь, поскольку просто никогда не умел составлять уравнения дифференциально преобразованных кривых (это ведь они образуют срез? похоже на эвольвенту).
При e -> 0 площадь фигуры стремится к 0.
Кстати, как вставить символ «эпсилон»?
По поводу двух кругов с бесконечно тонкой палочкой есть некоторые соображения, сейчас напишу ниже.
Кстати, как вставить символ «эпсилон»?
По поводу двух кругов с бесконечно тонкой палочкой есть некоторые соображения, сейчас напишу ниже.
Согласен, невнимательно прочитал.
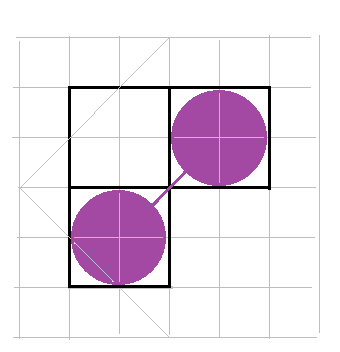
Тогда давайте рассматривать такой рисунок

Тогда давайте рассматривать такой рисунок

И в самом деле интересно, проще ли эта симметричная задача, чем несимметричная задача о перемещении дивана. Точное решение последней науке неизвестно.
Интересно, нельзя ли использовать решение классической задачи о перемещении дивана. Взять пересечение синей и красной фигуры на рисунке:

Правда в этом случае фигура получится не связной, но ведь об этом в условии не было сказано…

Правда в этом случае фигура получится не связной, но ведь об этом в условии не было сказано…
Кстати, площадь такой фигуры равна 2, так что её можно считать почти наилучшим решением. Его необычность состоит в том, что фигура состоит из двух не связанных между собой фрагментов, которые, однако, движутся как единое целое. Это формально не противоречит условию задачи.
Но поскольку в задаче речь шла всё-таки о плоте, имеет смысл уточнить условие и искать связную фигуру наибольшей площади, способную проплыть через канал.
Но поскольку в задаче речь шла всё-таки о плоте, имеет смысл уточнить условие и искать связную фигуру наибольшей площади, способную проплыть через канал.
> Кстати, площадь такой фигуры равна 2, так что её можно считать почти наилучшим решением.
Это не так.
> Это формально не противоречит условию задачи.
Давайте определимся с условиями. Я почему-то думал что раз речь идёт про плот, нужна связная фигура, иначе зачем бы мне соединять два круга? Если фигура несвязная всё гораздо проще. Но как-то нелогично, что фрагменты несвязной фигуры должны быть неподвижны друг относительно друга при движении.
Это не так.
> Это формально не противоречит условию задачи.
Давайте определимся с условиями. Я почему-то думал что раз речь идёт про плот, нужна связная фигура, иначе зачем бы мне соединять два круга? Если фигура несвязная всё гораздо проще. Но как-то нелогично, что фрагменты несвязной фигуры должны быть неподвижны друг относительно друга при движении.
Ох не нравятся мне красные поля перемещения центров симметрии в скринах выше. При подходе к узкому месту центр этих «песочных часов» получает неоправданную свободу.
Если взгляд меня не обманывает, к этим «песочным часам» можно надстроить сверху и снизу шапочки из «уголков» в стиле wirzus, тем самым сделав площадь ещё больше. После этого «красная площадь» (мн-во положений центров симметрии) должна превратиться в одну кривую. К сожалению, сейчас проверить не могу, только завтра.
Если взгляд меня не обманывает, к этим «песочным часам» можно надстроить сверху и снизу шапочки из «уголков» в стиле wirzus, тем самым сделав площадь ещё больше. После этого «красная площадь» (мн-во положений центров симметрии) должна превратиться в одну кривую. К сожалению, сейчас проверить не могу, только завтра.
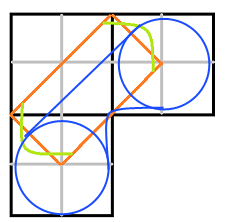
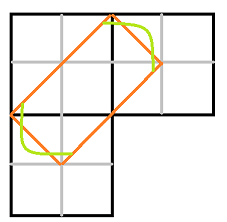
С сожалению, избавиться от красной площади не вышло. Синие уголки уменьшают размер красного участка только на то, что я выделил зелёным.

Итак, что у нас есть: два круга радиусом 1/2, фиолетовый участок от среза, образованный аналитическими кривыми и синий участок. Мда, получилась задачка сложнее, чем казалось. Предлагаю оставить её в покое рядом с диваном.

Итак, что у нас есть: два круга радиусом 1/2, фиолетовый участок от среза, образованный аналитическими кривыми и синий участок. Мда, получилась задачка сложнее, чем казалось. Предлагаю оставить её в покое рядом с диваном.
Попробую строго доказать, что фигура состоящая из двух кругов радиусами ½‒ɛ и ½ (решил, что можно только один только уменьшить, этого достаточно, а расчёты проще), соединённых линией НУЛЕВОЙ (для начала хватит) толщины и длины √2 «пройдёт» по коридору.
Пусть в произвольный момент времени центры кругов находятся в точках A и B соответственно. Наша фигура во время прохода угла постепенно поворачивается, обозначим угол поворота (против часовой стрелки) от начального положения как β. При прохождении угла величина β будет непрерывно расти от 0 до π/2, а круги будут «прижаты к внешним стенкам коридора», т.е. касаться их. Точка A всегда будет расположена на расстоянии радиуса первого круга (т.е. ½‒ɛ) от левой стенки, а точка B на расстоянии радиуса второго (½) от верхней. Центры кругов всегда будут находится на прямых, отстоящих на эти расстояния от стенок коридора и потому ни одна другая точка кругов не удалится больше чем на 2 радиуса от стенок коридора (1-2ɛ для первого и 1 для второго), что ограничивает все точки кругов коридором.
Итак, мы доказали весьма очевидное утверждение, что два круга соединённые отрезком длины √2 не выйдут за пределы круга. Ололо, поскольку мне не пришлось во время доказательства копировать символ √, получается, что я не использовал эту конкретную длину и доказал для любой, т.е. они могут быть плотно прижаты друг к другу или даже накладываться. У меня там дальше длинное доказательство, что отрезок тоже не выйдет за пределы, и потом я ещё буду делать переход от отрезков нулевой толщины к прямоугольникам малой толщины, а вы пока пока поразмышляйте над двумя сцеплёнными кругами, мне что-то не верится. Ведь если я прав, вторая часть доказательства просто не нужна.
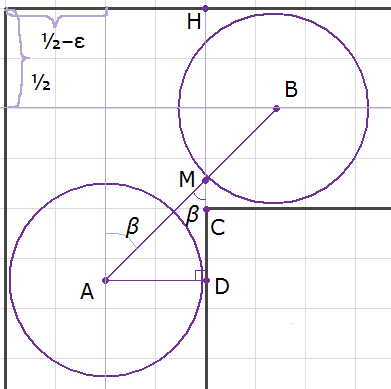
Пусть в произвольный момент времени центры кругов находятся в точках A и B соответственно. Наша фигура во время прохода угла постепенно поворачивается, обозначим угол поворота (против часовой стрелки) от начального положения как β. При прохождении угла величина β будет непрерывно расти от 0 до π/2, а круги будут «прижаты к внешним стенкам коридора», т.е. касаться их. Точка A всегда будет расположена на расстоянии радиуса первого круга (т.е. ½‒ɛ) от левой стенки, а точка B на расстоянии радиуса второго (½) от верхней. Центры кругов всегда будут находится на прямых, отстоящих на эти расстояния от стенок коридора и потому ни одна другая точка кругов не удалится больше чем на 2 радиуса от стенок коридора (1-2ɛ для первого и 1 для второго), что ограничивает все точки кругов коридором.
Итак, мы доказали весьма очевидное утверждение, что два круга соединённые отрезком длины √2 не выйдут за пределы круга. Ололо, поскольку мне не пришлось во время доказательства копировать символ √, получается, что я не использовал эту конкретную длину и доказал для любой, т.е. они могут быть плотно прижаты друг к другу или даже накладываться. У меня там дальше длинное доказательство, что отрезок тоже не выйдет за пределы, и потом я ещё буду делать переход от отрезков нулевой толщины к прямоугольникам малой толщины, а вы пока пока поразмышляйте над двумя сцеплёнными кругами, мне что-то не верится. Ведь если я прав, вторая часть доказательства просто не нужна.

Итак, зададимся теперь уже не столь актуальным вопросом, а не коснётся ли во время поворота отрезок AB угла коридора C? (Мне кажется очевидным доказать хотя бы для угла и отсюда на мой взгляд последуюет что и любой другой точки стенок коридора тоже не коснётся). Для случаев β=0 и β=π/2 всё вроде наглядно и проблем нет. Рассмотрим угол 0 < β < π/2. Прямые AB и CD (D — перпендикуляр из точки A на правую стенку коридора) пересекаются, т.к. β≠0. Обозначим их точку пересечения буквой M. Выясним, где относительно угла коридора C расположена точка M? Если выше, значит отрезок AB не касается внутреннего угла коридора. Чтобы выяснить, выше ли, вычислим длины отрезков DM и DC и сравним их между собой. Если DM > DC для любого β, значит точка M всегда выше C, и отрезок никогда не касается стенок коридора.
Итак: tgβ = AD/DM => DM = AD/tgβ,
ширина коридора = 1, A — на расстоянии ½‒ɛ от левой стенки, а значит на расстоянии 1-(½‒ɛ) от правой т.е. ½+ɛ. Расстояние от A до правой стенки по определению равно AD, значит DM = (½+ɛ)/tgβ,
DC = DH — CH (Не надо объяснять что такое H?). DH = ½+√2cosβ (сверху до B + катет треугольника с гипотенузой AB). CH=1 (ширина коридора). Значит DC = ½+√2cosβ‒1 = √2cosβ‒½.
Сравним DM = (½+ɛ)/tgβ и DC = √2cosβ‒½. Аналитически лень, так что вычтем из первого второе и построим график. Вот ɛ=0.05 график всегда выше оси абсцисс, значит DM > DC, что и т.д. Заметим, что для ɛ=0 есть точка, где разность равна нулю, т.е. если не уменьшать радиус круг на ɛ, то при повороте на некий угол (видимо π/4) отрезок коснётся угла коридора C. Т.е. мы не зря уменьшали радиус. И длина отрезка тоже учтена, наверное при другой эпсилона не хватит.
Добавлять отрезкам толщину я не буду. Это просто вычтет cosβ умноженный на очень малую толщину соединения из DM, причём эту толщину можно скомпенсировать соответсвующим эпсилоном.
Итак: tgβ = AD/DM => DM = AD/tgβ,
ширина коридора = 1, A — на расстоянии ½‒ɛ от левой стенки, а значит на расстоянии 1-(½‒ɛ) от правой т.е. ½+ɛ. Расстояние от A до правой стенки по определению равно AD, значит DM = (½+ɛ)/tgβ,
DC = DH — CH (Не надо объяснять что такое H?). DH = ½+√2cosβ (сверху до B + катет треугольника с гипотенузой AB). CH=1 (ширина коридора). Значит DC = ½+√2cosβ‒1 = √2cosβ‒½.
Сравним DM = (½+ɛ)/tgβ и DC = √2cosβ‒½. Аналитически лень, так что вычтем из первого второе и построим график. Вот ɛ=0.05 график всегда выше оси абсцисс, значит DM > DC, что и т.д. Заметим, что для ɛ=0 есть точка, где разность равна нулю, т.е. если не уменьшать радиус круг на ɛ, то при повороте на некий угол (видимо π/4) отрезок коснётся угла коридора C. Т.е. мы не зря уменьшали радиус. И длина отрезка тоже учтена, наверное при другой эпсилона не хватит.
Добавлять отрезкам толщину я не буду. Это просто вычтет cosβ умноженный на очень малую толщину соединения из DM, причём эту толщину можно скомпенсировать соответсвующим эпсилоном.
расмотрим картинку Laplace от 23 июля. Сдвиним центра А и В до соосности с точкой С. Получается фигура
типа «восьмёрка». Это цельный плот с площадью 1/8*(3пи+2)
типа «восьмёрка». Это цельный плот с площадью 1/8*(3пи+2)
А можно перевести на русский?
Окей, я писал об этом: Ололо, поскольку мне не пришлось во время доказательства копировать символ √, получается, что я не использовал эту конкретную длину и доказал для любой, т.е. они могут быть плотно прижаты друг к другу или даже накладываться.
Но какой смысл наложения? Площадь только меньше становится. Без наложения площадь стремится к π/2≈1.57, с наложением… 1/8*(3*π+2)≈1.43 (если верить Вашим расчётам).
Да и надо не просто придумать фигуру, а ещё строго доказать, что она решает поставленную задачу, чтоб никто потом не мог написать легко опровергается. Видно, что фигура «застряла» в таком положении. Она не может выйти и, на самом деле, никак не могла туда попасть. Невозможно указать точку, вокруг которой мы могли бы вращать фигуру, чтобы сместить её хотя бы на чуть-чуть. (хотя для всех подобных фигур с наложением я вроде доказал, что проходят).
Но какой смысл наложения? Площадь только меньше становится. Без наложения площадь стремится к π/2≈1.57, с наложением… 1/8*(3*π+2)≈1.43 (если верить Вашим расчётам).
Да и надо не просто придумать фигуру, а ещё строго доказать, что она решает поставленную задачу, чтоб никто потом не мог написать легко опровергается. Видно, что фигура «застряла» в таком положении. Она не может выйти и, на самом деле, никак не могла туда попасть. Невозможно указать точку, вокруг которой мы могли бы вращать фигуру, чтобы сместить её хотя бы на чуть-чуть. (хотя для всех подобных фигур с наложением я вроде доказал, что проходят).
Sign up to leave a comment.



Фигура максимальной площади, способная проплыть через канал