Хотя метод был разработан и представлен в 2001 году Полом Виолой и Майклом Джонсом [1, 2], он до сих пор на момент написания моего поста является основополагающим для поиска объектов на изображении в реальном времени [2]. По следам топика хабраюзера Indalo о данном методе, я попытался сам написать программу, которая распознает эмоцию на моём лице, но, к сожалению, не увидел на Хабре недостающей теории и описания работы некоторых алгоритмов, кроме указания их названий. Я решил собрать всё воедино, в одном месте. Сразу скажу, что свою программу успешно написал по данным алгоритмам. Как получилось рассказать о них ниже, решать Вам, уважаемые Хабрачитатели!
Итак, сразу к делу.
Основные принципы, на которых основан метод, таковы:
Обучение классификаторов идет очень медленно, но результаты поиска лица очень быстры, именно поэтому был выбран данный метод распознавания лиц на изображении. Виола-Джонс является одним из лучших по соотношению показателей эффективность распознавания/скорость работы. Также этот детектор обладает крайне низкой вероятностью ложного обнаружения лица. Алгоритм даже хорошо работает и распознает черты лица под небольшим углом, примерно до 30 градусов. При угле наклона больше 30 градусов процент обнаружений резко падает. И это не позволяет в стандартной реализации детектировать повернутое лицо человека под произвольным углом, что в значительной мере затрудняет или делает невозможным использование алгоритма в современных производственных системах с учетом их растущих потребностей.
Требуется подробный разбор принципов, на которых основан алгоритм Виолы-Джонса. Данный метод в общем виде ищет лица и черты лица по общему принципу сканирующего окна.
В общем виде, задача обнаружения лица и черт лица человека на цифровом изображении выглядит именно так:
Иными словами, применительно к рисункам и фотографиям используется подход на основе сканирующего окна (scanning window): сканируется изображение окном поиска (так называемое, окно сканирования), а затем применяется классификатор к каждому положению. Система обучения и выбора наиболее значимых признаков полностью автоматизирована и не требует вмешательства человека, поэтому данный подход работает быстро.
Задача поиска и нахождения лиц на изображении с помощью данного принципа часто бывает очередным шагом на пути к распознаванию характерных черт, к примеру, верификации человека по распознанному лицу или распознавания мимики лица.
Для того, чтобы производить какие-либо действия с данными, используется интегральное представление изображений [3] в методе Виолы-Джонса. Такое представление используется часто и в других методах, к примеру, в вейвлет-преобразованиях, SURF и многих других разобранных алгоритмах. Интегральное представление позволяет быстро рассчитывать суммарную яркость произвольного прямоугольника на данном изображении, причем какой бы прямоугольник не был, время расчета неизменно.
Интегральное представление изображения – это матрица, совпадающая по размерам с исходным изображением. В каждом элементе ее хранится сумма интенсивностей всех пикселей, находящихся левее и выше данного элемента. Элементы матрицы рассчитываются по следующей формуле:
 (1.2)
(1.2)
где I(i,j) — яркость пикселя исходного изображения.
Каждый элемент матрицы L[x,y] представляет собой сумму пикселей в прямоугольнике от (0,0) до (x,y), т.е. значение каждого пикселя (x,y) равно сумме значений всех пикселов левее и выше данного пикселя (x,y). Расчет матрицы занимает линейное время, пропорциональное числу пикселей в изображении, поэтому интегральное изображение просчитывается за один проход.
Расчет матрицы возможен по формуле 1.3:
По такой интегральной матрице можно очень быстро вычислить сумму пикселей произвольного прямоугольника, произвольной площади.
Пусть в прямоугольнике ABCD есть интересующий нас объект D:

Из рисунка понятно, что сумму внутри прямоугольника можно выразить через суммы и разности смежных прямоугольников по следующей формуле:
Примерный просчет показан на рисунке ниже:

Признак — отображение f: X => Df, где Df — множество допустимых значений признака. Если заданы признаки f1,…,fn, то вектор признаков x = (f1(x),…,fn(x)) называется признаковым описанием объекта x ∈ X. Признаковые описания допустимо отождествлять с самими объектами. При этом множество X = Df1* …* Dfn называют признаковым пространством [1].
Признаки делятся на следующие типы в зависимости от множества Df:
Естественно, бывают прикладные задачи с разнотипными признаками, для их решения подходят далеко не все методы.
В стандартном методе Виолы – Джонса используются прямоугольные признаки, изображенные на рисунке ниже, они называются примитивами Хаара:

В расширенном методе Виолы – Джонса, использующемся в библиотеке OpenCV используются дополнительные признаки:

Вычисляемым значением такого признака будет
где X – сумма значений яркостей точек закрываемых светлой частью признака, а Y – сумма значений яркостей точек закрываемых темной частью признака. Для их вычисления используется понятие интегрального изображения, рассмотренное выше.
Признаки Хаара дают точечное значение перепада яркости по оси X и Y соответственно.
Визуализация сканирующего окна в программе:

Алгоритм сканирования окна с признаками выглядит так:

В процессе поиска вычислять все признаки на маломощных настольных ПК просто нереально. Следовательно, классификатор должен реагировать только на определенное, нужное подмножество всех признаков. Совершенно логично, что надо обучить классификатор нахождению лиц по данному определенному подмножеству. Это можно сделать, обучая вычислительную машину автоматически.
Обучение машины — это процесс получения модулем новых знаний. Есть признанное определение данному процессу:

Данный процесс входит в концепцию и технологию под названием Data mining (извлечение информации и интеллектуальный анализ данных), куда входят помимо Машинного обучения такие дисциплины, как Теория баз данных, Искусственный интеллект, Алгоритмизация, Распознавание образов и прочие.
Машинное обучение в методе Виолы-Джонса решает такую задачу как классификация.
В контексте алгоритма, имеется множество объектов (изображений), разделённых некоторым образом на классы. Задано конечное множество изображений, для которых известно, к какому классу они относятся (к примеру, это может быть класс «фронтальное положение носа»). Это множество называется обучающей выборкой. Классовая принадлежность остальных объектов не известна. Требуется построить алгоритм, способный классифицировать произвольный объект из исходного множества [4].
Классифицировать объект — значит, указать номер (или наименование класса), к которому относится данный объект.
Классификация объекта — номер или наименование класса, выдаваемые алгоритмом классификации в результате его применения к данному конкретному объекту.
Классификатор(classifier) — в задачах классификации это аппроксимирующая функция, выносящая решение, к какому именно классу данный объект принадлежит.
Обучающая выборка – конечное число данных.
В машинном обучении задача классификации относится к разделу обучения с учителем когда классы поделены. Распознавание образов по сути своей и есть классификация изображений и сигналов. В случае алгоритма Виолы-Джонса для идентификации и распознавания лица классификация является двухклассовой.
Постановка классификации выглядит следующим образом:
Есть X – множество, в котором хранится описание объектов, Y – конечное множество номеров, принадлежащих классам. Между ними есть зависимость – отображение Y*: X => Y. Обучающая выборка представлена
Для решения проблемы данного, столь сложного обучения существует технология бустинга.
Бустинг — комплекс методов, способствующих повышению точности аналитических моделей. Эффективная модель, допускающая мало ошибок классификации, называется «сильной». «Слабая» же, напротив, не позволяет надежно разделять классы или давать точные предсказания, делает в работе большое количество ошибок. Поэтому бустинг (от англ. boosting – повышение, усиление, улучшение) означает дословно «усиление» «слабых» моделей [5] – это процедура последовательного построения композиции алгоритмов машинного обучения, когда каждый следующий алгоритм стремится компенсировать недостатки композиции всех предыдущих алгоритмов.
Идея бустинга была предложена Робертом Шапиром (Schapire) в конце 90-х годов [6], когда надо было найти решение вопроса о том, чтобы имея множество плохих (незначительно отличающихся от случайных) алгоритмов обучения, получить один хороший. В основе такой идеи лежит построение цепочки (ансамбля) классификаторов [5, 6], который называется каскадом, каждый из которых (кроме первого) обучается на ошибках предыдущего. Например, один из первых алгоритмов бустинга Boost1 использовал каскад из 3-х моделей, первая из которых обучалась на всем наборе данных, вторая – на выборке примеров, в половине из которых первая дала правильные ответы, а третья — на примерах, где «ответы» первых двух разошлись. Таким образом, имеет место последовательная обработка примеров каскадом классификаторов, причем так, что задача для каждого последующего становится труднее. Результат определяется путем простого голосования: пример относится к тому классу, который выдан большинством моделей каскада.
Бустинг представляет собой жадный алгоритм построения композиции алгоритмов (greedy algorithm) — это алгоритм, который на каждом шагу делает локально наилучший выбор в надежде, что итоговое решение будет оптимальным. Бустинг над решающими деревьями считается одним из наиболее эффективных методов с точки зрения качества классификации. Во многих экспериментах наблюдалось практически неограниченное уменьшение частоты ошибок на независимой тестовой выборке по мере наращивания композиции. Более того, качество на тестовой выборке часто продолжало улучшаться даже после достижения безошибочного распознавания всей обучающей выборки. Это перевернуло существовавшие долгое время представления о том, что для повышения обобщающей способности необходимо ограничивать сложность алгоритмов. На примере бустинга стало понятно, что хорошим качеством могут обладать сколь угодно сложные композиции, если их правильно настраивать [5].
Математически бустинг объянсяется так:
Наряду с множествами X и Y вводится вспомогательное множество R, называемое пространством оценок. Рассматриваются алгоритмы, имеющие вид суперпозиции a(x) = C(b(x)), где функция b: X → R называется алгоритмическим оператором, функция C: R → Y –решающим правилом.
Многие алгоритмы классификации имеют именно такую структуру: сначала вычисляются оценки принадлежности объекта классам, затем решающее правило переводит эти оценки в номер класса. Значение оценки, как правило, характеризует степень уверенности классификации.
Алгоритмическая композиция – алгоритм a: X → Y вида
, составленный из алгоритмических операторов bt :X→R, t=1,..., T, корректирующей операции F: RT→R и решающего правила C: R→Y.
Базовыми алгоритмами обозначаются функции at(x) = C(bt(x)), а при фиксированном решающем правиле C — и сами операторы bt(x).
Суперпозиции вида F(b1,..., bT ) являются отображениями из X в R, то есть, опять же, алгоритмическими операторами.
В задачах классификации на два непересекающихся класса в качестве пространства оценок обычно используется множество действительных чисел. Решающие правила могут иметь настраиваемые параметры. Так, в алгоритме Виолы-Джонса используется пороговое решающее правило, где, как правило, сначала строится оператор при нулевом значении, а затем подбирается значение оптимальное. Процесс последовательного обучения базовых алгоритмов применяется, пожалуй, чаще всего при построении композиций.
Критерии останова могут использоваться различные, в зависимости от специфики задачи, возможно также совместное применение нескольких критериев:
Развитием данного подхода явилась разработка более совершенного семейства алгоритмов бустинга AdaBoost (adaptive boosting – адаптированное улучшение), предложенная Йоавом Фройндом (Freund) и Робертом Шапиром (Schapire) в 1999 году [9], который может использовать произвольное число классификаторов и производить обучение на одном наборе примеров, поочередно применяя их на различных шагах.
Рассматривается задача классификации на два класса, Y = {−1,+1}. К примеру, базовые алгоритмы также возвращают только два ответа −1 и +1, и решающее правило фиксировано: C(b) = sign(b). Искомая алгоритмическая композиция имеет вид:
 (1.7)
(1.7)
Функционал качества композиции Qt определяется как число ошибок, допускаемых ею на обучающей выборке:
 (1.8)
(1.8)
где Wl = (w1, …, wl) – вектор весов объектов.
Для решения задачи AdaBoosting’а нужна экспоненциальная аппроксимация пороговой функции потерь [z<0], причем экспонента Ez = e-z (видно на рисунке, демонстрирующем работу AdaBoost ниже).
Итак, общий алгоритм адаптивного усиления, AdaBoost, выглядит следующим образом:
Реализация AdaBoost на этапах подготовки, 2ого шага, 12ого и 642ого показана на рисунке. После построения некоторого количества базовых алгоритмов (скажем, пары десятков) нужно проанализировать распределение весов объектов. Объекты с наибольшими весами wi, возможно, являются шумовыми выбросами, которые стоит исключить из выборки, после чего начать построение композиции заново.

Плюсы AdaBoost:
Минусы AdaBoost:
В наши дни подход усиления простых классификаторов является популярным и, вероятно, наиболее эффективным методом классификации за счёт высокой скорости и эффективности работы и относительной простоты реализации.
Дерево принятия решений — это дерево, в листьях которого стоят значения целевой функции, а в остальных узлах — условия перехода (к примеру, на Лице есть Улыбка), определяющие по какому из ребер идти. Если для данного наблюдения условие равно истине то осуществляется переход по левому ребру, если же ложь — по правому [4]. Для примера, дерево представлено на следующем рисунке:

Примерный алгоритм создания решающего дерева приведен ниже:
Достоинствами таких решающих деревьев являются наглядность, легкость работы с ними, быстродействие. Также, они легко применяются для задач с множеством классов.
Алгоритм бустинга для поиска лиц с моей точки зрения таков:
1. Определение слабых классификаторов по прямоугольным признакам;
2. Для каждого перемещения сканирующего окна вычисляется прямоугольный признак на каждом примере;
3. Выбирается наиболее подходящий порог для каждого признака;
4. Отбираются лучшие признаки и лучший подходящий порог;
5. Перевзвешивается выборка.
Каскадная модель сильных классификаторов – это по сути то же дерево принятия решений, где каждый узел дерева построен таким образом, чтобы детектировать почти все интересующие образы и отклонять регионы, не являющиеся образами. Помимо этого, узлы дерева размещены таким образом, что чем ближе узел находится к корню дерева, тем из меньшего количества примитивов он состоит и тем самым требует меньшего времени на принятие решения. Данный вид каскадной модели хорошо подходит для обработки изображений, на которых общее количество детектируемых образов мало.
В этом случае метод может быстрее принять решение о том, что данный регион не содержит образ, и перейти к следующему. Пример каскадной модели сильных классификаторов:
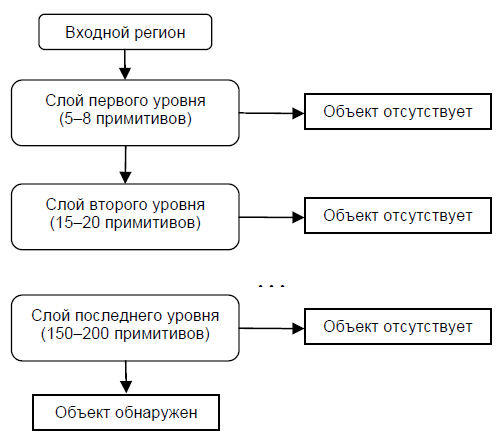
Сложность обучения таких каскадов равна О(xyz), где применяется x этапов, y примеров и z признаков.
Далее, каскад применяется к изображению:
1. Работа с «простыми» классификаторами – при этом отбрасывается часть «отрицательных» окон;
2. Положительное значение первого классификатора запускает второй, более приспособленный и так далее;
3. Отрицательное значение классификатора на любом этапе приводит к немедленному переходу к следующему сканирующему окну, старое окно отбрасывается;
4. Цепочка классификаторов становится более сложной, поэтому ошибок становится намного меньше.
Для тренировки такого каскада потребуются следующие действия:
1. Задаются значения уровня ошибок для каждого этапа (предварительно их надо количественно просмотреть при применении к изображению из обучающего набора) – они называются detection и false positive rates – надо чтобы уровень detection был высок, а уровень false positive rates низок;
2. Добавляются признаки до тех пор, пока параметры вычисляемого этапа не достигнут поставленного уровня, тут возможны такие вспомогательные этапы, как:
а. Тестирование дополнительного маленького тренировочного набора;
б. Порог AdaBoost умышленно понижается с целью найти больше объектов, но в связи с этим возможно большее число неточных определений объектов;
3. Если false positive rates остается высоким, то добавляется следующий этап или слой;
4. Ложные обнаружения в текущем этапе используются как отрицательные уже на следующем слое или этапе.
В более формальном виде алгоритм тренировки каскада задан ниже:
Был подробно рассмотрен механизм работы алгоритма Виолы-Джонса (Viola-Jones). Можно улучшить данный метод и модифицировать его, чего я добился в своей написанной программе — об этом будет рассказано в следующем моем топике.
1. P. Viola and M.J. Jones, «Rapid Object Detection using a Boosted Cascade of Simple Features», proceedings IEEE Conf. on Computer Vision and Pattern Recognition (CVPR 2001), 2001
2. P. Viola and M.J. Jones, «Robust real-time face detection», International Journal of Computer Vision, vol. 57, no. 2, 2004., pp.137–154
3. Р.Гонсалес, Р.Вудс, «Цифровая обработка изображений», ISBN 5-94836-028-8, изд-во: Техносфера, Москва, 2005. – 1072 с.
4. Местецкий Л. М., «Математические методы распознавания образов», МГУ, ВМиК, Москва, 2002–2004., с. 42 – 44
5. Jan ˇSochman, Jiˇr´ı Matas, «AdaBoost», Center for Machine Perception, Czech Technical University, Prague, 2010
6. Yoav Freund, Robert E. Schapire, «A Short Introduction to Boosting», Shannon Laboratory, USA, 1999., pp. 771-780
P.S. За появление данной статьи благодарю тех людей, которые плюсанули позавчера мне, и у меня появилось 2 балла кармы, а следовательно, появилась возможность представить данную статью ХабраЮзерам. Всем хороших предстоящих выходных!
Итак, сразу к делу.
Описание метода Viola Jones
Основные принципы, на которых основан метод, таковы:
- используются изображения в интегральном представлении, что позволяет вычислять быстро необходимые объекты;
- используются признаки Хаара, с помощью которых происходит поиск нужного объекта (в данном контексте, лица и его черт);
- используется бустинг (от англ. boost – улучшение, усиление) для выбора наиболее подходящих признаков для искомого объекта на данной части изображения;
- все признаки поступают на вход классификатора, который даёт результат «верно» либо «ложь»;
- используются каскады признаков для быстрого отбрасывания окон, где не найдено лицо.
Обучение классификаторов идет очень медленно, но результаты поиска лица очень быстры, именно поэтому был выбран данный метод распознавания лиц на изображении. Виола-Джонс является одним из лучших по соотношению показателей эффективность распознавания/скорость работы. Также этот детектор обладает крайне низкой вероятностью ложного обнаружения лица. Алгоритм даже хорошо работает и распознает черты лица под небольшим углом, примерно до 30 градусов. При угле наклона больше 30 градусов процент обнаружений резко падает. И это не позволяет в стандартной реализации детектировать повернутое лицо человека под произвольным углом, что в значительной мере затрудняет или делает невозможным использование алгоритма в современных производственных системах с учетом их растущих потребностей.
Требуется подробный разбор принципов, на которых основан алгоритм Виолы-Джонса. Данный метод в общем виде ищет лица и черты лица по общему принципу сканирующего окна.
Принцип сканирующего окна
В общем виде, задача обнаружения лица и черт лица человека на цифровом изображении выглядит именно так:
- имеется изображение, на котором есть искомые объекты. Оно представлено двумерной матрицей пикселей размером w*h, в которой каждый пиксель имеет значение:
—от 0 до 255, если это черно-белое изображение;
—от 0 до 2553, если это цветное изображение (компоненты R, G, B). - в результате своей работы, алгоритм должен определить лица и их черты и пометить их – поиск осуществляется в активной области изображения прямоугольными признаками, с помощью которых и описывается найденное лицо и его черты:
rectanglei = {x,y,w,h,a},(1.1)
где x, y – координаты центра i-го прямоугольника, w – ширина, h – высота, a – угол наклона прямоугольника к вертикальной оси изображения.
Иными словами, применительно к рисункам и фотографиям используется подход на основе сканирующего окна (scanning window): сканируется изображение окном поиска (так называемое, окно сканирования), а затем применяется классификатор к каждому положению. Система обучения и выбора наиболее значимых признаков полностью автоматизирована и не требует вмешательства человека, поэтому данный подход работает быстро.
Задача поиска и нахождения лиц на изображении с помощью данного принципа часто бывает очередным шагом на пути к распознаванию характерных черт, к примеру, верификации человека по распознанному лицу или распознавания мимики лица.
Интегральное представление изображений
Для того, чтобы производить какие-либо действия с данными, используется интегральное представление изображений [3] в методе Виолы-Джонса. Такое представление используется часто и в других методах, к примеру, в вейвлет-преобразованиях, SURF и многих других разобранных алгоритмах. Интегральное представление позволяет быстро рассчитывать суммарную яркость произвольного прямоугольника на данном изображении, причем какой бы прямоугольник не был, время расчета неизменно.
Интегральное представление изображения – это матрица, совпадающая по размерам с исходным изображением. В каждом элементе ее хранится сумма интенсивностей всех пикселей, находящихся левее и выше данного элемента. Элементы матрицы рассчитываются по следующей формуле:
 (1.2)
(1.2)где I(i,j) — яркость пикселя исходного изображения.
Каждый элемент матрицы L[x,y] представляет собой сумму пикселей в прямоугольнике от (0,0) до (x,y), т.е. значение каждого пикселя (x,y) равно сумме значений всех пикселов левее и выше данного пикселя (x,y). Расчет матрицы занимает линейное время, пропорциональное числу пикселей в изображении, поэтому интегральное изображение просчитывается за один проход.
Расчет матрицы возможен по формуле 1.3:
L(x,y) = I(x,y) – L(x-1,y-1) + L(x,y-1) + L(x-1,y) (1.3)По такой интегральной матрице можно очень быстро вычислить сумму пикселей произвольного прямоугольника, произвольной площади.
Пусть в прямоугольнике ABCD есть интересующий нас объект D:

Из рисунка понятно, что сумму внутри прямоугольника можно выразить через суммы и разности смежных прямоугольников по следующей формуле:
S(ABCD) = L(A) + L(С) — L(B) — L(D) (1.4)Примерный просчет показан на рисунке ниже:

Признаки Хаара
Признак — отображение f: X => Df, где Df — множество допустимых значений признака. Если заданы признаки f1,…,fn, то вектор признаков x = (f1(x),…,fn(x)) называется признаковым описанием объекта x ∈ X. Признаковые описания допустимо отождествлять с самими объектами. При этом множество X = Df1* …* Dfn называют признаковым пространством [1].
Признаки делятся на следующие типы в зависимости от множества Df:
- бинарный признак, Df = {0,1};
- номинальный признак: Df — конечное множество;
- порядковый признак: Df — конечное упорядоченное множество;
- количественный признак: Df — множество действительных чисел.
Естественно, бывают прикладные задачи с разнотипными признаками, для их решения подходят далеко не все методы.
В стандартном методе Виолы – Джонса используются прямоугольные признаки, изображенные на рисунке ниже, они называются примитивами Хаара:

В расширенном методе Виолы – Джонса, использующемся в библиотеке OpenCV используются дополнительные признаки:

Вычисляемым значением такого признака будет
F = X-Y, (1.5)где X – сумма значений яркостей точек закрываемых светлой частью признака, а Y – сумма значений яркостей точек закрываемых темной частью признака. Для их вычисления используется понятие интегрального изображения, рассмотренное выше.
Признаки Хаара дают точечное значение перепада яркости по оси X и Y соответственно.
Сканирование окна
Визуализация сканирующего окна в программе:

Алгоритм сканирования окна с признаками выглядит так:
- есть исследуемое изображение, выбрано окно сканирования, выбраны используемые признаки;
- далее окно сканирования начинает последовательно двигаться по изображению с шагом в 1 ячейку окна (допустим, размер самого окна есть 24*24 ячейки);
- при сканировании изображения в каждом окне вычисляется приблизительно 200 000 вариантов расположения признаков, за счет изменения масштаба признаков и их положения в окне сканирования;
- сканирование производится последовательно для различных масштабов;
- масштабируется не само изображение, а сканирующее окно (изменяется размер ячейки);
- все найденные признаки попадают к классификатору, который «выносит вердикт».

В процессе поиска вычислять все признаки на маломощных настольных ПК просто нереально. Следовательно, классификатор должен реагировать только на определенное, нужное подмножество всех признаков. Совершенно логично, что надо обучить классификатор нахождению лиц по данному определенному подмножеству. Это можно сделать, обучая вычислительную машину автоматически.
Используемая в алгоритме модель машинного обучения
Обучение машины — это процесс получения модулем новых знаний. Есть признанное определение данному процессу:
«Машинное обучение — это наука, изучающая компьютерные алгоритмы, автоматически улучшающиеся во время работы» (Michel, 1996). Ниже показан процесс обучения машины:

Данный процесс входит в концепцию и технологию под названием Data mining (извлечение информации и интеллектуальный анализ данных), куда входят помимо Машинного обучения такие дисциплины, как Теория баз данных, Искусственный интеллект, Алгоритмизация, Распознавание образов и прочие.
Машинное обучение в методе Виолы-Джонса решает такую задачу как классификация.
Обучение классификатора в методе Виолы-Джонса
В контексте алгоритма, имеется множество объектов (изображений), разделённых некоторым образом на классы. Задано конечное множество изображений, для которых известно, к какому классу они относятся (к примеру, это может быть класс «фронтальное положение носа»). Это множество называется обучающей выборкой. Классовая принадлежность остальных объектов не известна. Требуется построить алгоритм, способный классифицировать произвольный объект из исходного множества [4].
Классифицировать объект — значит, указать номер (или наименование класса), к которому относится данный объект.
Классификация объекта — номер или наименование класса, выдаваемые алгоритмом классификации в результате его применения к данному конкретному объекту.
Классификатор(classifier) — в задачах классификации это аппроксимирующая функция, выносящая решение, к какому именно классу данный объект принадлежит.
Обучающая выборка – конечное число данных.
В машинном обучении задача классификации относится к разделу обучения с учителем когда классы поделены. Распознавание образов по сути своей и есть классификация изображений и сигналов. В случае алгоритма Виолы-Джонса для идентификации и распознавания лица классификация является двухклассовой.
Постановка классификации выглядит следующим образом:
Есть X – множество, в котором хранится описание объектов, Y – конечное множество номеров, принадлежащих классам. Между ними есть зависимость – отображение Y*: X => Y. Обучающая выборка представлена
Xm = {(x1,y1), …, (xm,ym)}. Конструируется функция f от вектора признаков X, которая выдает ответ для любого возможного наблюдения X и способна классифицировать объект x∈X. Данное простое правило должно хорошо работать и на новых данных.Применяемый в алгоритме бустинг и разработка AdaBoost
Для решения проблемы данного, столь сложного обучения существует технология бустинга.
Бустинг — комплекс методов, способствующих повышению точности аналитических моделей. Эффективная модель, допускающая мало ошибок классификации, называется «сильной». «Слабая» же, напротив, не позволяет надежно разделять классы или давать точные предсказания, делает в работе большое количество ошибок. Поэтому бустинг (от англ. boosting – повышение, усиление, улучшение) означает дословно «усиление» «слабых» моделей [5] – это процедура последовательного построения композиции алгоритмов машинного обучения, когда каждый следующий алгоритм стремится компенсировать недостатки композиции всех предыдущих алгоритмов.
Идея бустинга была предложена Робертом Шапиром (Schapire) в конце 90-х годов [6], когда надо было найти решение вопроса о том, чтобы имея множество плохих (незначительно отличающихся от случайных) алгоритмов обучения, получить один хороший. В основе такой идеи лежит построение цепочки (ансамбля) классификаторов [5, 6], который называется каскадом, каждый из которых (кроме первого) обучается на ошибках предыдущего. Например, один из первых алгоритмов бустинга Boost1 использовал каскад из 3-х моделей, первая из которых обучалась на всем наборе данных, вторая – на выборке примеров, в половине из которых первая дала правильные ответы, а третья — на примерах, где «ответы» первых двух разошлись. Таким образом, имеет место последовательная обработка примеров каскадом классификаторов, причем так, что задача для каждого последующего становится труднее. Результат определяется путем простого голосования: пример относится к тому классу, который выдан большинством моделей каскада.
Бустинг представляет собой жадный алгоритм построения композиции алгоритмов (greedy algorithm) — это алгоритм, который на каждом шагу делает локально наилучший выбор в надежде, что итоговое решение будет оптимальным. Бустинг над решающими деревьями считается одним из наиболее эффективных методов с точки зрения качества классификации. Во многих экспериментах наблюдалось практически неограниченное уменьшение частоты ошибок на независимой тестовой выборке по мере наращивания композиции. Более того, качество на тестовой выборке часто продолжало улучшаться даже после достижения безошибочного распознавания всей обучающей выборки. Это перевернуло существовавшие долгое время представления о том, что для повышения обобщающей способности необходимо ограничивать сложность алгоритмов. На примере бустинга стало понятно, что хорошим качеством могут обладать сколь угодно сложные композиции, если их правильно настраивать [5].
Математически бустинг объянсяется так:
Наряду с множествами X и Y вводится вспомогательное множество R, называемое пространством оценок. Рассматриваются алгоритмы, имеющие вид суперпозиции a(x) = C(b(x)), где функция b: X → R называется алгоритмическим оператором, функция C: R → Y –решающим правилом.
Многие алгоритмы классификации имеют именно такую структуру: сначала вычисляются оценки принадлежности объекта классам, затем решающее правило переводит эти оценки в номер класса. Значение оценки, как правило, характеризует степень уверенности классификации.
Алгоритмическая композиция – алгоритм a: X → Y вида
a(x) = C(F(b1(x), . . . , bT (x)), x ∈ X (1.6), составленный из алгоритмических операторов bt :X→R, t=1,..., T, корректирующей операции F: RT→R и решающего правила C: R→Y.
Базовыми алгоритмами обозначаются функции at(x) = C(bt(x)), а при фиксированном решающем правиле C — и сами операторы bt(x).
Суперпозиции вида F(b1,..., bT ) являются отображениями из X в R, то есть, опять же, алгоритмическими операторами.
В задачах классификации на два непересекающихся класса в качестве пространства оценок обычно используется множество действительных чисел. Решающие правила могут иметь настраиваемые параметры. Так, в алгоритме Виолы-Джонса используется пороговое решающее правило, где, как правило, сначала строится оператор при нулевом значении, а затем подбирается значение оптимальное. Процесс последовательного обучения базовых алгоритмов применяется, пожалуй, чаще всего при построении композиций.
Критерии останова могут использоваться различные, в зависимости от специфики задачи, возможно также совместное применение нескольких критериев:
- построено заданное количество базовых алгоритмов T;
- достигнута заданная точность на обучающей выборке;
- достигнутую точность на контрольной выборке не удаётся улучшить на протяжении последних нескольких шагов при определенном параметре алгоритма.
Развитием данного подхода явилась разработка более совершенного семейства алгоритмов бустинга AdaBoost (adaptive boosting – адаптированное улучшение), предложенная Йоавом Фройндом (Freund) и Робертом Шапиром (Schapire) в 1999 году [9], который может использовать произвольное число классификаторов и производить обучение на одном наборе примеров, поочередно применяя их на различных шагах.
Рассматривается задача классификации на два класса, Y = {−1,+1}. К примеру, базовые алгоритмы также возвращают только два ответа −1 и +1, и решающее правило фиксировано: C(b) = sign(b). Искомая алгоритмическая композиция имеет вид:
 (1.7)
(1.7)Функционал качества композиции Qt определяется как число ошибок, допускаемых ею на обучающей выборке:
 (1.8)
(1.8)где Wl = (w1, …, wl) – вектор весов объектов.
Для решения задачи AdaBoosting’а нужна экспоненциальная аппроксимация пороговой функции потерь [z<0], причем экспонента Ez = e-z (видно на рисунке, демонстрирующем работу AdaBoost ниже).
Итак, общий алгоритм адаптивного усиления, AdaBoost, выглядит следующим образом:
Дано:
- Y = {−1,+1},
- b1(x), . . . , bT (x) возвращают −1 и + 1,
- Xl – обучающая выборка.
Решение:
1. Инициализация весов объектов:
wi:= 1/ℓ, i = 1, . . . , ℓ; (1.9)
для всех t = 1, . . . , T, пока не выполнен критерий останова:
2 а.  (1.10)
(1.10)
2 б.  (1.11)
(1.11)
3. Пересчёт весов объектов. Правило мультипликативного пересчёта весов. Вес объекта увеличивается в  раз, когда bt допускает на нём ошибку, и во столько же раз уменьшается, когда bt правильно классифицирует xi. Таким образом, непосредственно перед настройкой базового алгоритма наибольший вес накапливается у тех объектов, которые чаще оказывались трудными для предыдущих алгоритмов:
раз, когда bt допускает на нём ошибку, и во столько же раз уменьшается, когда bt правильно классифицирует xi. Таким образом, непосредственно перед настройкой базового алгоритма наибольший вес накапливается у тех объектов, которые чаще оказывались трудными для предыдущих алгоритмов:
 (1.12)
(1.12)
4. Нормировка весов объектов:
 (1.13)
(1.13)
Реализация AdaBoost на этапах подготовки, 2ого шага, 12ого и 642ого показана на рисунке. После построения некоторого количества базовых алгоритмов (скажем, пары десятков) нужно проанализировать распределение весов объектов. Объекты с наибольшими весами wi, возможно, являются шумовыми выбросами, которые стоит исключить из выборки, после чего начать построение композиции заново.

Плюсы AdaBoost:
- хорошая обобщающая способность. В реальных задачах практически всегда строятся композиции, превосходящие по качеству базовые алгоритмы. Обобщающая способность может улучшаться по мере увеличения числа базовых алгоритмов;
- простота реализации;
- собственные накладные расходы бустинга невелики. Время построения композиции практически полностью определяется временем обучения базовых алгоритмов;
- возможность идентифицировать объекты, являющиеся шумовыми выбросами. Это наиболее «трудные» объекты xi, для которых в процессе наращивания композиции веса wi принимают наибольшие значения.
Минусы AdaBoost:
- Бывает переобучение при наличии значительного уровня шума в данных. Экспоненциальная функция потерь слишком сильно увеличивает веса «наиболее трудных» объектов, на которых ошибаются многие базовые алгоритмы. Однако именно эти объекты чаще всего оказываются шумовыми выбросами. В результате AdaBoost начинает настраиваться на шум, что ведёт к переобучению. Проблема решается путём удаления выбросов или применения менее «агрессивных» функций потерь. В частности, применяется алгоритм GentleBoost;
- AdaBoost требует достаточно длинных обучающих выборок. Другие методы линейной коррекции, в частности, бэггинг, способны строить алгоритмы сопоставимого качества по меньшим выборкам данных;
- Бывает построение неоптимального набора базовых алгоритмов. Для улучшения композиции можно периодически возвращаться к ранее построенным алгоритмам и обучать их заново.
- Бустинг может приводить к построению громоздких композиций, состоящих из сотен алгоритмов. Такие композиции исключают возможность содержательной интерпретации, требуют больших объёмов памяти для хранения базовых алгоритмов и существенных временных затрат на вычисление классификаций.
В наши дни подход усиления простых классификаторов является популярным и, вероятно, наиболее эффективным методом классификации за счёт высокой скорости и эффективности работы и относительной простоты реализации.
Принципы решающего дерева в разрабатываемом алгоритме
Дерево принятия решений — это дерево, в листьях которого стоят значения целевой функции, а в остальных узлах — условия перехода (к примеру, на Лице есть Улыбка), определяющие по какому из ребер идти. Если для данного наблюдения условие равно истине то осуществляется переход по левому ребру, если же ложь — по правому [4]. Для примера, дерево представлено на следующем рисунке:

Примерный алгоритм создания решающего дерева приведен ниже:
function Node = Обучение_Вершины( {(x,y)} ) {
if {y} одинаковые
return Создать_Лист(y);
test = Выбрать_лучшее_разбиение( {(x,y)} );
{(x0,y0)} = {(x,y) | test(x) = 0};
{(x1,y1)} = {(x,y) | test(x) = 1};
LeftChild = Обучение_Вершины( {(x0,y0)} );
RightChild = Обучение_Вершины( {(x1,y1)} );
return Создать_Вершину(test, LeftChild, RightChild);
}
//Обучение дерева
function main() {
{(X,Y)} = Прочитать_Обучающие_Данные();
TreeRoot = Обучение_Вершины( {(X,Y)} );
}
Достоинствами таких решающих деревьев являются наглядность, легкость работы с ними, быстродействие. Также, они легко применяются для задач с множеством классов.
Каскадная модель разрабатываемого алгоритма
Алгоритм бустинга для поиска лиц с моей точки зрения таков:
1. Определение слабых классификаторов по прямоугольным признакам;
2. Для каждого перемещения сканирующего окна вычисляется прямоугольный признак на каждом примере;
3. Выбирается наиболее подходящий порог для каждого признака;
4. Отбираются лучшие признаки и лучший подходящий порог;
5. Перевзвешивается выборка.
Каскадная модель сильных классификаторов – это по сути то же дерево принятия решений, где каждый узел дерева построен таким образом, чтобы детектировать почти все интересующие образы и отклонять регионы, не являющиеся образами. Помимо этого, узлы дерева размещены таким образом, что чем ближе узел находится к корню дерева, тем из меньшего количества примитивов он состоит и тем самым требует меньшего времени на принятие решения. Данный вид каскадной модели хорошо подходит для обработки изображений, на которых общее количество детектируемых образов мало.
В этом случае метод может быстрее принять решение о том, что данный регион не содержит образ, и перейти к следующему. Пример каскадной модели сильных классификаторов:

Сложность обучения таких каскадов равна О(xyz), где применяется x этапов, y примеров и z признаков.
Далее, каскад применяется к изображению:
1. Работа с «простыми» классификаторами – при этом отбрасывается часть «отрицательных» окон;
2. Положительное значение первого классификатора запускает второй, более приспособленный и так далее;
3. Отрицательное значение классификатора на любом этапе приводит к немедленному переходу к следующему сканирующему окну, старое окно отбрасывается;
4. Цепочка классификаторов становится более сложной, поэтому ошибок становится намного меньше.
Для тренировки такого каскада потребуются следующие действия:
1. Задаются значения уровня ошибок для каждого этапа (предварительно их надо количественно просмотреть при применении к изображению из обучающего набора) – они называются detection и false positive rates – надо чтобы уровень detection был высок, а уровень false positive rates низок;
2. Добавляются признаки до тех пор, пока параметры вычисляемого этапа не достигнут поставленного уровня, тут возможны такие вспомогательные этапы, как:
а. Тестирование дополнительного маленького тренировочного набора;
б. Порог AdaBoost умышленно понижается с целью найти больше объектов, но в связи с этим возможно большее число неточных определений объектов;
3. Если false positive rates остается высоким, то добавляется следующий этап или слой;
4. Ложные обнаружения в текущем этапе используются как отрицательные уже на следующем слое или этапе.
В более формальном виде алгоритм тренировки каскада задан ниже:
a) Пользователь задает значения f (максимально допустимый уровень ложных срабатываний на слой) и d (минимально допустимый уровень обнаружений на слой)
b) Пользователь задает целевой общий уровень ложных срабатываний Ftarget
c) P – набор положительных примеров
d) N – набор отрицательных примеров
e) F0 = 1,0; D0 = 1,0; i = 0
f) while ( Fi > Ftarget)
i = i+1; ni = 0; Fi = Fi-1
while (Fi = f * Fi-1 )
ni = ni + 1
AdaBoost(P, N, ni)
Оценить полученный каскад на тестовом наборе для определения Fi и Di ;
Уменьшать порог для i-того классификатора, пока текущий каскад будет иметь уровень обнаружения по крайней мере d*Di-1 (это же касается Fi) ;
g) N = Ø;
h) Если Fi > Ftarget , то оценить текущий каскад на наборе изображений, не содержащих лиц, и добавить все неправильно классифицированные в N.
Выводы
Был подробно рассмотрен механизм работы алгоритма Виолы-Джонса (Viola-Jones). Можно улучшить данный метод и модифицировать его, чего я добился в своей написанной программе — об этом будет рассказано в следующем моем топике.
Список литературы:
1. P. Viola and M.J. Jones, «Rapid Object Detection using a Boosted Cascade of Simple Features», proceedings IEEE Conf. on Computer Vision and Pattern Recognition (CVPR 2001), 2001
2. P. Viola and M.J. Jones, «Robust real-time face detection», International Journal of Computer Vision, vol. 57, no. 2, 2004., pp.137–154
3. Р.Гонсалес, Р.Вудс, «Цифровая обработка изображений», ISBN 5-94836-028-8, изд-во: Техносфера, Москва, 2005. – 1072 с.
4. Местецкий Л. М., «Математические методы распознавания образов», МГУ, ВМиК, Москва, 2002–2004., с. 42 – 44
5. Jan ˇSochman, Jiˇr´ı Matas, «AdaBoost», Center for Machine Perception, Czech Technical University, Prague, 2010
6. Yoav Freund, Robert E. Schapire, «A Short Introduction to Boosting», Shannon Laboratory, USA, 1999., pp. 771-780
P.S. За появление данной статьи благодарю тех людей, которые плюсанули позавчера мне, и у меня появилось 2 балла кармы, а следовательно, появилась возможность представить данную статью ХабраЮзерам. Всем хороших предстоящих выходных!