Я не могу написать бинарный поиск

Недавно (буквально два года назад) тут пробегала статья Только 10% программистов способны написать двоичный поиск. Двоичный поиск — это классический алгоритм поиска. Мало того, это еще чрезвычайно простой алгоритм, который можно очень легко описать: берем отсортированный массив, смотрим в середину, если не нашли там число, в зависимости от того, что в середине — ищем это число этим же методом либо в левой части, либо в правой, откидывая средний элемент. Для функций также, просто берем не массив, а функцию. Все очень и очень просто, алгоритм описан почти везде, все баги словлены и описаны.

Так вот, я не могу реализовать двоичный поиск. Для меня он ни капельки не тривиален. Наверное, я ненастоящий программист. А ведь так и есть, я всего-лишь студент, но ведь это не оправдание? Если точнее, я не могу реализовать хороший корректный красивый двоичный поиск. Все время у меня вылезает проблема либо с корректностью, либо с красивостью, либо и с тем, и с другим. Так что, да, заголовок немного желтоват.
Прежде чем читать этот топик, напишите свою версию бинарного поиска — для отсортированного массива. Причем, в зависимости от параметра, поиск должен выдавать или первый элемент, или любой из дублирующих. Еще для сравнения, напишите бинарный поиск для функций

Для начала, я буду писать код на C#. Я надеюсь, поклонники других языков с легкостью поймут мой код. Границы поиска я буду представлять в виде полуинтервала [left; right), т.е. точка left включается, а точка right выключается. Для меня полуинтервалы удобнее, к их поведению я уже привык, кроме того, использование полуинтервалов имеет некоторые преимущества при программировании различных алгоритмов (о чем мы поговорим позже). Вообще, использовать полуинтервалы более правильно с точки зрения поддержки «единого стиля программирования», так как я пишу циклы вот так:

for (int i = 0; i < array.Length; i++)

а не так:

for (int i = 0; i <= array.Length - 1; i++)

Я буду писать одновременно рекурсивную и итеративную версию, но мне ближе рекурсивная, так что не обессудьте. Для рекурсивной версии мы сделаем вот такую вот красивую обертку:

static int BinarySearch_Rec_Wrapper(int[] array, int element)
{
    BinarySearch_Rec(array, element, 0, array.Length);
}

Первая попытка

Итак, давайте напишем первую версию бинпоиска для отсортированного массива. Для начала, нам нужно уметь вычислять индекс среднего элемента. Окей, допустим мы очень умные и уже знаем, что обычный способ

int mid = (left + right) / 2 

вызовет переполнение на больших массивах, и поэтому будем использовать более правильный метод (см. ссылку в начале статьи):

 int mid = left + (right - left) / 2

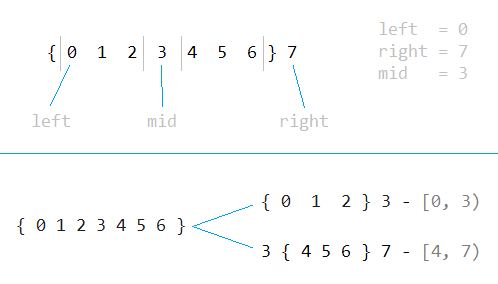
При разработке алгоритмов очень полезно рисовать на листочке пример входных данных, ваши действия и результат. Иначе рискуете нарваться на ошибку типа off-by-one. К примеру, для первого шага можно нарисовать такую картинку:

Это дает хорошее понимание, что массив надо бить на интервал от [0, 3) и от [4, 7), т.е. от [left, mid) и до [mid + 1, right). Надо заметить, что существовала еще и «нулевая» версия (для статьи), в которой индексы были написаны по памяти, и, естественно, написаны они были неправильно. Самое интересное, что если я пишу алгоритм на листочке, то никаких ошибок не появляется, а если пишу на компьютере, они вылазят как грибы после дождя.

Кстати, теперь можно добавить еще одну причину к использованию полуинтервалов: если у нас есть интервал [left, right], то мы должны его разбить на [left, mid — 1] и [mid + 1; right] (что конечно, чуть проще для запоминания, но весьма странно).
У полуинтервалов различие в индексах равно 1 (одному элементу, который мы выбрасываем), а у интервалов — 2 — магической цифре, взятой с потолка.

Особенно это заметно для сортировки слиянием, где для полуинтервалов различия в индексах нету (массив делится на [left, mid) и [mid, right)), а для интервалов появляется различие равное 1 (так как массив делится на [left, mid] и [mid + 1, right], или [left, mid — 1] и [mid, right]).

Теперь, осталось определить, в какой части массива нужно искать элемент, в зависимости от того, меньше ли средний элемент (array[mid]), чем ключ (key). Сделать это весьма просто — нужно просто подставить сначала один знак, проверить, работает ли программа, а если не работает, то другой :-). Почему-то именно такой способ проверки я и использую. Мне постоянно кажется, что перекомпилировать быстрее, чем «подумать».

Рекурсивно:

static int BinarySearch_Rec(int[] array, int key, int left, int right)
{
    int mid = left + (right - left) / 2;

    if (array[mid] == key)
        return mid;

    else if (array[mid] > key)
        return BinarySearch_Rec(array, key, left, mid);
    else
        return BinarySearch_Rec(array, key, mid + 1, right);
}

Итеративно:

static int BinarySearch_Iter(int[] array, int key)
{
    int left = 0;
    int right = array.Length;

    while (true)
    {
        int mid = left + (right - left) / 2;

        if (array[mid] == key)
            return mid;

        if (array[mid] > key)
            right = mid;
        else
            left = mid + 1;
    }
}

Разбор полетов:

Если внимательно вчитаться в итеративную версию программы, то сразу становится понятно, что если элемента нет, то алгоритм никогда не остановится. Пониманию этого факта очень способствует while(true), которого в рекурсивной версии программы, естественно нет. И хотя я написал кучу реализаций рекурсивных алгоритмов, я все еще иногда сталкиваюсь с тем, что забываю остановить рекурсию. Как можно написать итеративную версию с подвохом, я не знаю.

Вторая попытка

Хорошо, нам надо останавливать алгоритм, когда мы не можем найти элемент в массиве. Но мы же должны что-то возвратить, верно? Или хотя-бы кинуть исключение. Что возвратить? Может быть магическое число (к примеру, -1)? Или заменить int на int? и возвратить null? (int? в c# — это число, которому можно присвоить null). Или может быть вернуть предполагаемое место в массиве, где мог-бы быть элемент, но его нет? Или все-таки кинуть исключение? Или… Это достаточно интересный вопрос, почти такой же как и «в чем смысл жизни?». Кроме интересности, эти вопросы объединяет тот факт, что ответ на оба вопроса можно сформулировать следующим образом: что хотите, то и выбирайте. Конечно, найдутся люди, которые скажут, что нужно возвращать только null, и только null.

Я предпочитаю в таком случае возвратить специальное число -(1 + left), так как, бинарный поиск может использоваться для того, чтобы вставить новый элемент, и потеря информации будет вредна. Конечно, можно написать две версии алгоритма — одна будет возвращать специальное число, а вторая кидать исключение. Хотя это и нехорошо для принципа DRY, если в вашем языке нету чего-нибудь мощного вроде макросов, которые создают функции при компиляции. Ну или можно засунуть в алгоритм параметр, обозначающий что делать.

Кстати, останавливать рекурсию мы будем в случае left == right, т.е., когда интервал стал таким — [left, right). Ну или в случае, когда right — left < 1 или right — left <= 0. Последний, кстати, полезнее, поскольку нам могли передать что-то не то в функцию (в итеративную версию, там где нету обертки).

Рекурсивно:

static int BinarySearch_Rec(int[] array, int key, int left, int right)
{
    int mid = left + (right - left) / 2;

    if (left >= right)
        return -(1 + left);

    if (array[mid] == key)
        return mid;

    else if (array[mid] > key)
        return BinarySearch_Rec(array, key, left, mid);
    else
        return BinarySearch_Rec(array, key, mid + 1, right);
}

Итеративно:

static int BinarySearch_Iter(int[] array, int key)
{
    int left = 0;
    int right = array.Length;
    int mid = 0;

    while (!(left >= right))
    {
        mid = left + (right - left) / 2;

        if (array[mid] == key)
            return mid;

        if (array[mid] > key)
            right = mid;
        else
            left = mid + 1;
    }

    return -(1 + left);
}

Разбор полетов:

Нам никто не говорил, что массив отсортирован по возрастанию. Поэтому нам нужно вычислить, в каком порядке находятся числа в массиве, и уже в зависимости от этого выбирать нужную половину для поиска. Кстати, вычислять нужно всего-лишь раз, так что к итеративной версии тоже придется дописывать обертку.

Попытка №3

Нужно придумать, как выбирать нужную половину для поиска. Самая первая моя попытка содержала и ||, и &&, после чего мне повезло заметить, что все это сводится к банальнейшему XOR'у:

descendingOrder	array[mid] > key	XOR
0	0	0
0	1	1
1	0	1
1	1	0

Т.е. если флаг descendingOrder не установлен, то выбор идет как обычно, если установлен, то выбор идет наоборот. Но это «хак», и возможно, что нужно написать какой-нибудь комментарий. Я не знаю, что именно он должен содержать.

Рекурсивно:

static int BinarySearch_Rec(int[] array, bool descendingOrder, int key, int left, int right)
{
    int mid = left + (right - left) / 2;

    if (left >= right)
        return -(1 + left);

    if (array[mid] == key)
        return mid;

    else if ((array[mid] > key) ^ descendingOrder)
        return BinarySearch_Rec(array, descendingOrder, key, left, mid);
    else
        return BinarySearch_Rec(array, descendingOrder, key, mid + 1, right);
}

static int BinarySearch_Rec_Wrapper(int[] array, int key)
{
	if (array.Length == 0)
        return -1;

    bool descendingOrder = array[0] > array[array.Length - 1];
    return BinarySearch_Rec(array, descendingOrder, key, 0, array.Length);
}

Итеративно:

static int BinarySearch_Iter(int[] array, bool descendingOrder, int key)
{
    int left = 0;
    int right = array.Length;
    int mid = 0;

    while (!(left >= right))
    {
        mid = left + (right - left) / 2;

        if (array[mid] == key)
            return mid;

        if ((array[mid] > key) ^ descendingOrder)
            right = mid;
        else
            left = mid + 1;
    }

    return -(1 + left);
}

static int BinarySearch_Iter_Wrapper(int[] array, int key)
{
	if (array.Length == 0)
    	return -1;

    bool descendingOrder = array[0] > array[array.Length - 1];
    return BinarySearch_Iter(array, descendingOrder, key);
}

Разбор полетов:

На всякий случай: один из вариантов проверки направления сортировки не учитывал, что массив может быть пуст. Я решил не выделять этот фейл в отдельную попытку.

Попытка №4

Теперь нужно сделать так, чтобы алгоритм искал первый элемент из равных. Для этого надо додуматься как минимум до одной «нетривиальной» идеи — не выбрасывать из области поиска уже найденный элемент, если у нас нет других кандидатов. Не знаю, что было со мной, когда я первый раз пытался это реализовать… Но я не догадался до этого.
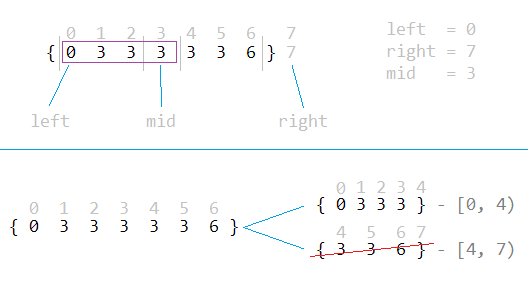
Нарисуем шаг, когда мы уже нашли один элемент, который равен ключу и нам нужно найти первый элемент из одинаковых:

Дабы мы не попали на еще одну попытку, сразу скажу, что теперь рекурсию нужно останавливать еще и в случае, когда самый первый элемент из полуинтервала равен ключу. Ну а в случае, когда мы узнали, что средний элемент равен ключу у нас есть два варианта. Либо средний следует за первым и нужно выдавать именно его, ибо первый не равен ключу, поскольку рекурсия еще не остановилась. Либо нужно укорачивать область поиска (см. картинку выше)

Рекурсивно:

static int BinarySearch_Rec(int[] array, bool descendingOrder, int key, int left, int right)
{
    int mid = left + (right - left) / 2;

    if (left >= right)
        return -(1 + left);

    if (array[left] == key)
        return left;

    if (array[mid] == key)
    {
        if (mid == left + 1)
            return mid;
        else
            return BinarySearch_Rec(array, descendingOrder, key, left, mid + 1);
    }

    else if ((array[mid] > key) ^ descendingOrder)
        return BinarySearch_Rec(array, descendingOrder, key, left, mid);
    else
        return BinarySearch_Rec(array, descendingOrder, key, mid + 1, right);
}

static int BinarySearch_Rec_Wrapper(int[] array, int key)
{
    if (array.Length == 0)
        return -1;

    bool descendingOrder = array[0] > array[array.Length - 1];
    return BinarySearch_Rec(array, descendingOrder, key, 0, array.Length);
}

Итеративно:

static int BinarySearch_Iter(int[] array, bool descendingOrder, int key)
{
    int left = 0;
    int right = array.Length;
    int mid = 0;

    while (!(left >= right))
    {
        mid = left + (right - left) / 2;

        if (array[left] == key)
            return left;

        if (array[mid] == key)
        {
            if (mid == left + 1)
                return mid;
            else
                right = mid + 1;
        }

        else if ((array[mid] > key) ^ descendingOrder)
            right = mid;
        else
            left = mid + 1;
    }

    return -(1 + left);
}

static int BinarySearch_Iter_Wrapper(int[] array, int key)
{
    if (array.Length == 0)
        return -1;

    bool descendingOrder = array[0] > array[array.Length - 1];
    return BinarySearch_Iter(array, descendingOrder, key);
}

Попытка №5

Теперь нам нужно написать унифицированный алгоритм, который работает для любых направлений сортировок, и для поиска либо первого, либо последнего, либо любого элемента из дублирующих. Я не хочу повторять этот ужас, поэтому просто скопипастю то, что писал некоторое время назад:

Вы правда хотите это видеть?

Оно вам надо?

Я вас предупреждал

enum ElementToChoose
{
	First,
	Last,
	NoCare
}

/// <summary>
/// Finds element equal to value in sorted array in range [low, high)
/// </summary>
static int binarySearch(int value, int[] array, bool ascendingOrder, ElementToChoose elementToChoose, int low, int high) {
	// return valid invalid position
	if (low >= high)
		return -(low + 1);

	// return first or last found element
	if (elementToChoose == ElementToChoose.First)
		if (value == array[low])
			return low;

	int last = high - 1;

	if (elementToChoose == ElementToChoose.Last)
		if (value == array[last])
			return last;

	int mid = low + (high - low) / 2;

	// we have found some element
	if (value == array[mid]) {
		switch (elementToChoose) {
			case ElementToChoose.NoCare:
				return mid;

			case ElementToChoose.First:
				if (mid - low <= 1)
					// array[mid] is the earliest element in array, return it
					// because array[low] != value && array[low+1] == value, where mid == low + 1
					return mid;
				else
					// try to find first element
					// don't forget to capture current element {|0, 0|, 1} -> {0, 0}
					return binarySearch(value, array, ascendingOrder, elementToChoose, low, mid + 1);
			case ElementToChoose.Last:
				if (last - mid <= 1)
					// array[mid] is the last element in array, return it
					// because array[last] != value && array[last - 1] == value, where mid == last - 1
					return mid;
				else
					// try to find last element
					// don't forget to capture current element {0, |0, 1|} -> {0, 1}
					return binarySearch(value, array, ascendingOrder, elementToChoose, mid, high);
		}
	}

	// choose left or right half, depending on sorting order & comparing value and mid
	if ((value < array[mid]) ^ !ascendingOrder)
		return binarySearch(value, array, ascendingOrder, elementToChoose, low, mid);
	else
		return binarySearch(value, array, ascendingOrder, elementToChoose, mid + 1, high);
}

Что плохого в этом коде, помимо того что он ужасен и комментарии написаны на непонятном языке? Этот код позволяет задуматься, а почему нельзя было написать 3 варианта поиска, а не городить малопонятного монстрика? Нет, если присмотреться, он вполне неплох, хотя и плох (если сравнить с другими версиями выше).

Кстати, я сейчас подумал, что гораздо красивее представлять интервалы в виде объектов с волшебными свойствами/методами getFirstHalf, getSecondHalf (получают первую и вторую половину интервала), getStartPoint/getLastPoint (получают первую/последнюю точку интервала), increaseLength/decreaseLength (меняют длину интервала), moveStartPoint. Ну или еще какими-нибудь другими волшебными свойствами. Это чрезвычайно упростило бы понимание двоичного поиска, да и вообще любых алгоритмов.

Бинарный поиск по монотонной функции

Для того, чтобы написать алгоритм, нам нужно будет использовать числа с плавающей точкой. Плавающая точка… Если вы еще не произносите рефлекторно мат, когда слышите словосочетание «плавающая точка», значит вы плохо с ней работали. Давайте посмотрим код:

// для нешарпистов - Func<float, float> функция, принимающая float и отдающая float
static float BinarySearch_Func(Func<float, float> func, bool descendingOrder, float key, float left, float right)
{
    float mid = (left + right) / 2;

    if (left == mid || mid == right)
        return mid;

    if ((func(mid) > key) ^ descendingOrder)
        return BinarySearch_Func(func, descendingOrder, key, left, mid);
    else
        return BinarySearch_Func(func, descendingOrder, key, mid, right);
}

static float BinarySearch_Func_Wrapper(Func<float, float> func, float key, float left, float right)
{
    if (left > right)
        return float.NaN;

    bool descendingOrder = func(left) > func(right);
    bool isOk = true;

    if (!descendingOrder)
        isOk = func(left) <= key && key <= func(right);
    else
        isOk = func(right) <= key && key <= func(left);

    if (isOk)
        return BinarySearch_Func(func, descendingOrder, key, left, right);
    else
        return float.NaN;
}

Задайте себе несколько вопросов. Этот код работает? Почему он работает? Что за прикол с абсолютным сравнением float'ов? (если у вас не вызывает этот момент удивления, прошу читать статью Что нужно знать про арифметику с плавающей запятой?, возможно, найдете что-нибудь полезное).
Хотите еще один клевый вопрос? Каков тип интервала left; right? Это [left, right], или [left, right), или (left, right], или (left, right)? Внимательно подумайте. Запустите этот кусок кода и подумайте еще раз:

// Для нешарпистов x => x - лямбда-запись функции f(x) = x
Console.WriteLine(BinarySearch_Func_Wrapper(x => x, 0.7f, 0.7f, 100.0f)); // Вывод: 0.7
Console.WriteLine(BinarySearch_Func_Wrapper(x => x, 0.8f, 0.8f, 100.0f)); // Вывод: 0,8000001
Console.WriteLine(BinarySearch_Func_Wrapper(x => x, 0.9f, 0.9f, 100.0f)); // Вывод: 0,9

Console.WriteLine("{0:0.00000000}",0.8f); // Вывод: 0,80000000

Итак, точка left у нас включается и исключается в зависимости от погоды на Марсе. Для точки right погода на Марсе тоже имеет важное значение (проверено). Т.е. мы складываем два числа a и b, делим сумму на два и получаем либо a, либо b, либо что-то между ними. Это забавно.
На самом деле, эта фишка скорее всего прописана в стандарте, а может, вычисление mid зависит от опций компилятора/платформы. А может действительно от погоды на Марсе.

Чтобы соблюсти хоть какой-то контракт, нам нужно в обертку поместить проверки func(left) == key и func(right) == key, тогда наши интервалы всегда будут закрытыми с обоих сторон.

В качестве задачки, кому скучно будет: попытайтесь скрестить поиск по массиву с поиском по функции, покажите своего монстра.
Те, кому не настолько скучно, могут показать хотя-бы альтернативные примеры реализаций бин. поиска, более красивые или с чуть-другими идеями.
Те, кому очень-очень скучно, я предлагаю такую задачку: напишите бинарный поиск по функции, если все числа — рациональные, и представляются в виде несократимой дроби a/b. В качестве очень жестокого издевательства: числа a и b безграничные. Супер-сложность: все еще за O(lgn).

Вообще, хочется спросить: а что все-таки лучше — одна монструозная функция, которая поддерживает выбор первого/последнего/любого из них или три функции, чрезвычайно похожих, но немного не таких?

P.S: вполне возможно, что в моем коде есть ошибки. Буду благодарен, если укажите на них
P.P.S: а какие комментарии должны быть к такому алгоритму?

UPD1: Юзер fox_anthony предложил вместо -(1 + left) писать ~left. Подробнее: Оператор ~, msdn, c#