Motion planning: граф видимости, дорожные карты

[@withkittens]

Спасибо за статью. Пожалуйста, пишите ещё, буду рад вас почитать.

[@Trimax]

Спасибо.

[@ZumZoom]

Хорошо пишете. Добавлю от себя немного :)

1. Существует более быстрый вариант построения графа видимости, использующий Rotation Trees. Асимптотически работает за O(n^2), а пишется даже быстрее чем алгоритм с заметающей прямой по углу. Почитать можно здесь.
2. Вместо Грэхэма лучше писать Грэхэма с оптимизациями Эндрю. Асимптотически они одинаковы, но в варианте Эндрю сортировка работает быстрее за счет упрощения операций сравнения.
3. Вы почему-то решили не указывать оставшихся двух авторов книги Computational Geometry, а зря, потому что они обязательно должны быть упомянуты в любой содержательной статье по вычислительной геометрии :)

[@Trimax]

Спасибо. Господ M. van Kreveld и M. Overmars добавил. Странно что я их продинамил. Что касается Rotation Trees, большое спасибо — обязательно прочитаю.

[@evilkost]

Знаком немного с темой в контексте роботики и мне кажется, самый интиресный алгоритм — это RRT* ).
Еще стоит не забывать о габаритах персонажа и кинематике движения, иначе можно получить нереализумый путь.

[@Trimax]

Да, «как есть» этот алгоритм использовать не получится. К тому же, вряд ли все ходят по стеночкам. :) Нужно добавлять потенциалы вершинам или заведомо увеличивать полигоны.

[@Zibx]

Я уже давно хожу по стеночкам после исследования этих самых алгоритмов :).

[@stanislaw]

На Java есть либа решающая подобные задачи Straightedge

[@Trimax]

Спасибо за ссылку, думаю будет полезно.

[@Shc]

Можно доказать, что оптимальный путь — это кусочно-линейная ломаная, вершины которой совпадают с вершинами препятствий.

Ой ли? ;)

рисунок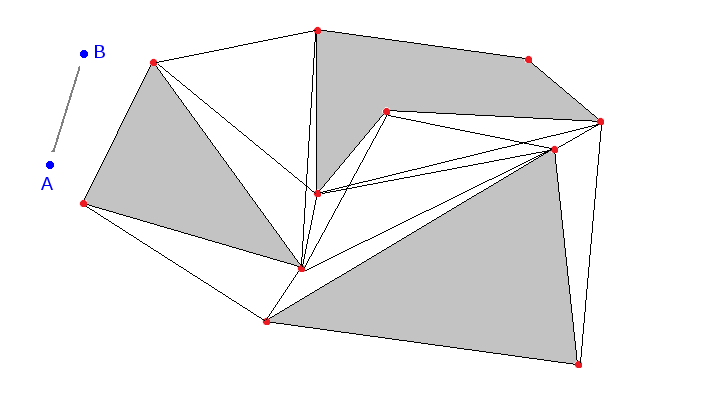

[@ZumZoom]

Кроме начальной и конечной, естественно, потому что они заданы изначально.

[@Trimax]

Это, разумеется, понятно. Это вырожденный случай. К тому же, ведь путь мы ищем на расширенном графе, в который добавлены вершины s & f.

[@Shc]

оно как бы понятно, что такой вариант тривиальный :)
я просто к тому, что исходя из описанных условий задачи он не вписывается в доказательство оптимального пути :)
но это просто что-то между вредностью, стебом и занудством — особо не парьтесь :)

[@Trimax]

Понял. Да я тоже педант, каюсь, проглядел. :)

[@DoctorGester]

А можно сурс приложения с последнего скриншота?