В задачах машинного зрения и автоматизированной обработки изображений зачастую встречается задача бесшовного наложения изображений. Для наглядности, сразу приведу пример.

Бесшовным наложением изображений (блендингом) будем называть метод, позволяющий вставить часть одного изображения в другое так, чтобы не было заметно швов на границах вставляемого изображения. Данный метод как бы подстраивает вставляемую часть под остальное изображение. На самом деле для получения результата используется только градиентное поле вставляемой части и значения пикселей исходного изображения на границе обрабатываемой области.
Пусть у нас имеются изображения А, на которое в определенном месте накладывается изображение В.

Для бесшовного блендинга необходимо чтобы градиент изображения А в области изображения В равнялся градиенту изображения В. Восстановление цвета на области В будет осуществляться на основе градиента в области В и данных о цвете изображения А на границе области В.
Это означает что для получения результирующего изображения необходимо восстановить изображение по его градиенту, т.е. решить задачу Пуассона.
Ниже приведено решение поставленной задачи для монотонного изображения. Для RGB изображения метод применяется к каждому каналу.
Определим границу вставляемой области следующим образом:
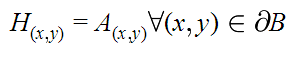
И вычислим градиент накладываемого изображения:
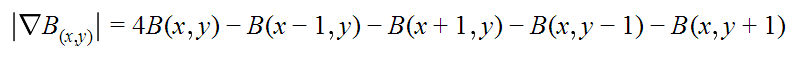
Теперь все данные имеются и мы можем составить уравнение Пуассона:
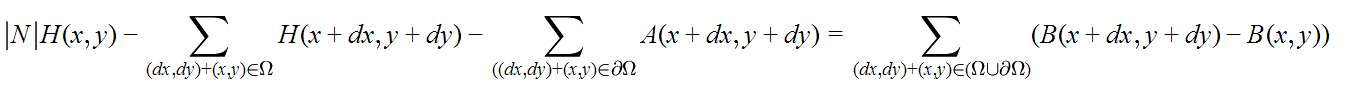
где (x, y) — координата текущего пикселя, N — число соседних пикселей не включая границы (не более 4), (dx, dy) — координаты соседних пикселей, могут принимать значения из множества {(-1, 0), (1, 0), (0, -1), (0, 1)}
Таким образом, для каждого неизвестного пикселя составляется уравнение. В итоге мы получим систему с M неизвестными, где М — число пикселей вставляемого изображения. Остается только решить эту систему. Методов для решения этой довольно много, но для решения обычно используют метод Якоби и метод Гаусса-Зейделя.
Зачастую, в накладываемой области смешивают градиентное поле с исходным изображением. Например, берут максимальное значение градиентов А или В в определенной точки. Лучше всего почувствовать разницу между исходным и комбинированным градиентом на примере.
Восстановление по градиенту изображения В:

Восстановление по максимальному градиенту изображений А и В:

Очевидно, что восстановление изображения по комбинированному градиенту целесообразно применять для объектов, имеющий прозрачную структуру (вода, радуга, облака и т. п.).
А вот как бы выглядело наложение радуги без комбинации градиентов
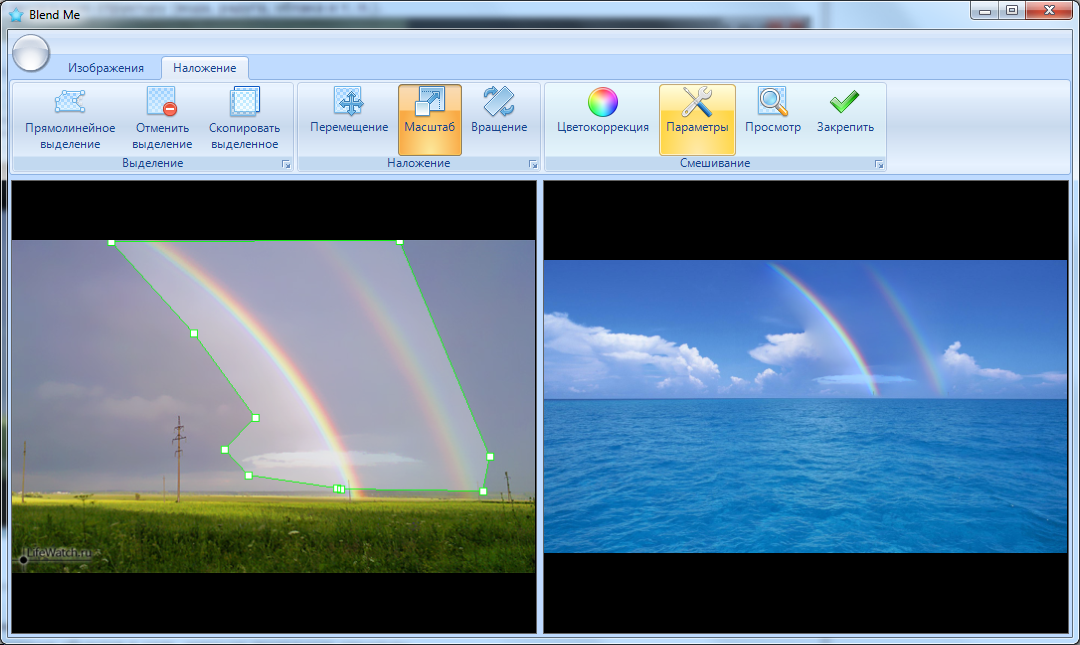

Бесшовным наложением изображений (блендингом) будем называть метод, позволяющий вставить часть одного изображения в другое так, чтобы не было заметно швов на границах вставляемого изображения. Данный метод как бы подстраивает вставляемую часть под остальное изображение. На самом деле для получения результата используется только градиентное поле вставляемой части и значения пикселей исходного изображения на границе обрабатываемой области.
Постановка задачи
Пусть у нас имеются изображения А, на которое в определенном месте накладывается изображение В.

Для бесшовного блендинга необходимо чтобы градиент изображения А в области изображения В равнялся градиенту изображения В. Восстановление цвета на области В будет осуществляться на основе градиента в области В и данных о цвете изображения А на границе области В.
Это означает что для получения результирующего изображения необходимо восстановить изображение по его градиенту, т.е. решить задачу Пуассона.
Ниже приведено решение поставленной задачи для монотонного изображения. Для RGB изображения метод применяется к каждому каналу.
Решение
Определим границу вставляемой области следующим образом:
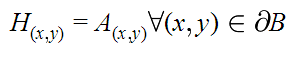
И вычислим градиент накладываемого изображения:
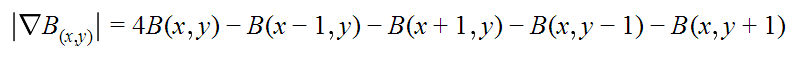
Теперь все данные имеются и мы можем составить уравнение Пуассона:
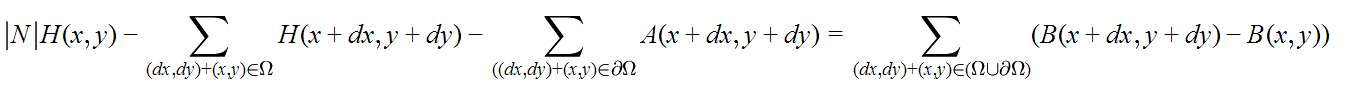
где (x, y) — координата текущего пикселя, N — число соседних пикселей не включая границы (не более 4), (dx, dy) — координаты соседних пикселей, могут принимать значения из множества {(-1, 0), (1, 0), (0, -1), (0, 1)}
Таким образом, для каждого неизвестного пикселя составляется уравнение. В итоге мы получим систему с M неизвестными, где М — число пикселей вставляемого изображения. Остается только решить эту систему. Методов для решения этой довольно много, но для решения обычно используют метод Якоби и метод Гаусса-Зейделя.
Зачастую, в накладываемой области смешивают градиентное поле с исходным изображением. Например, берут максимальное значение градиентов А или В в определенной точки. Лучше всего почувствовать разницу между исходным и комбинированным градиентом на примере.
Восстановление по градиенту изображения В:

Восстановление по максимальному градиенту изображений А и В:

Очевидно, что восстановление изображения по комбинированному градиенту целесообразно применять для объектов, имеющий прозрачную структуру (вода, радуга, облака и т. п.).

А вот как бы выглядело наложение радуги без комбинации градиентов

Применение преобразование блендинга Пуассона
- Замена лиц / вставка новых объектов в кадр
- Наложение объектов в кадр, имеющих прозрачную структуру
- Сглаживание изображений при создании панорам
- Сглаживание изображений при создании 3D-моделей объектов
Ссылки
- Оригинальная статья
- Немного теории, применение и примеры
- Решение СЛАУ методом Якоби и методом Гаусса — Зейделя + исходники
- Программа + исходники на Java
- Фото сделаны с помощью программы Blend Me
