По поисковому запросу шум перлина сразу попадается этот перевод на Хабре. Как справедливо заметили в комментариях к публикации, речь идёт вовсе не о шуме Перлина. Возможно, автор перевода и сам был не в курсе.
Чем выгодно отличается шум Перлина,легко можно заметить, если сравнить картинки.
Обычный шум (из той самой статьи):

Шум Перлина:

И увеличением количества октав первую картинку ко второй никак не приблизишь. Я не буду описывать достоинства шума Перлина и область его применения (потому что статья о программировании, а не о применении), а постараюсь объяснить как он реализован. Думаю, это будет полезно многим программистам, ведь хакерские исходники Кена Перлина мало объясняют даже при наличии комментариев.
Поразительно, но судя по отзывам в личку и в комментарии оказалось, что далеко не все способны видеть вообще какую-либо разницу между простым сглаженным шумом в градациях серого и шумом Перлина. Но, наверное, из-за этого парадокса и появилась и поимела популярность та самая статья.
Попробую дать наводку:
первая картинка состоит из явно выраженных пикселей (увеличенных) разных оттенков серого:

Вторая же (шум Перлина) выглядит как черно-белые размытые черви.
Вот что получается после несложных операций в графическом редакторе (поиск границ, инвертирование, постеризация):
Перлин:

Картинка из статьи (применены точно те же операции):

Да, во фрактальном шуме, если октав много, то понять, что там лежит в оригинале — Перлин или нет уже и правда сложно. Но это ведь не повод назвать фрактальный шум Шумом Перлина.
На этом закончу с описанием разницы.
Конец отступления.
Рассмотрим двухмерный вариант. Пока напишем только класс-заготовку. Входящие данные — двухмерный вектор или два числа с плавающей точкой: x, y.
Возвращаемое значение — число от -1.0 до 1.0:
Идея обычного сглаженного шума в том, что есть дискретная сетка псевдослучайных значений, и для запрашиваемой точки происходит интерполяция между узлами сетки (чем ближе точка к какому-нибудь узлу сетки, тем больше его значение соответствует значению узла).
Здесь в третьем условном квадрате точка в самом центре после интерполяции будет иметь значение 3:
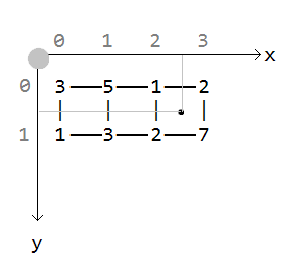
Рассмотрим детальнее как там получается тройка. Координаты точки:
Целочисленные координаты точки (верхний левый угол квадрата):
получаются округлением в меньшую сторону (функция floor).
Локальные координаты точки внутри квадрата получаются вычитанием:
Берём значение левого верхнего угла квадрата (1) и верхнего правого (2). Интерполируем верхнюю грань используя локальную координату x (0.5). Линейная интерполяция выглядит так:
Берём значение левого нижнего угла квадрата (2) и нижнего правого (7). Интерполируем нижнюю грань используя всё ту же локальную координату x (0.5).
Результаты:
Теперь осталась интерполяция верхней и нижней с использованием локальной координаты y (тоже 0.5):
Билинейная интерполяция самая простая но и результат не самый привлекательный.
Другие варианты интерполяции подразумевают модифицирование локальной координаты (параметра t) перед интерполяцией. Получаются более плавные переходы возле граничных значений (0 и 1).
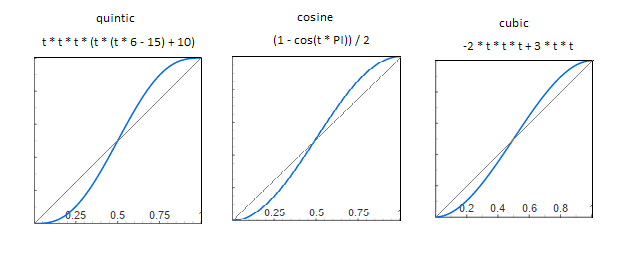
В шуме Перлина задействован первый вариант, он даёт достаточно сильное искривление.
Всё очень просто:
1. В узлах сетки — псевдослучайные вектора (двухмерные для двухмерного шума, трехмерные для трехмерного и так далее), а не псевдослучайные числа.
2. Интерполируем между скалярными произведениями a) векторов от вершин квадрата до точки внутри квадрата (куба в трехмерном варианте) и b) псевдослучайных векторов (при описании шума Перлина их называют градиентными векторами).
В своём улучшенном варианте шума Кен Перлин использует всего 12 градиентных векторов. Для двухмерного варианта требуется всего 4 — по количеству граней (у квадрата их 4). Вектора направлены (условно из центра куба/квадрата) в сторону каждой из граней и не нормализованы.
Вот они:
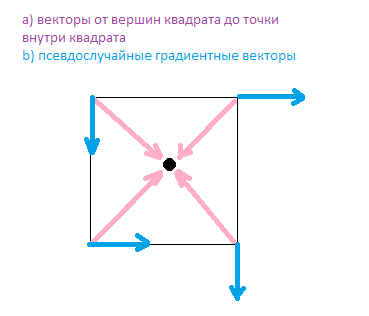
Итак, каждому узлу сетки соответствует один из четырёх векторов. Пусть вектор у нас будет массивом float-ов.
Нам понадобится скалярное произведение векторов:
Главный метод:
В качестве бонуса:
И последнее — использование таблицы со случайными числами. В коде Кена Перлина такая таблица прописана вручную и достаются оттуда значения совсем по-другому. Здесь можно экспериментировать и от этого немало зависит равномерность шума и отсутствие в нём явных паттернов.
Я сделал
Результат:

Чем выгодно отличается шум Перлина,
Обычный шум (из той самой статьи):

Шум Перлина:

И увеличением количества октав первую картинку ко второй никак не приблизишь. Я не буду описывать достоинства шума Перлина и область его применения (потому что статья о программировании, а не о применении), а постараюсь объяснить как он реализован. Думаю, это будет полезно многим программистам, ведь хакерские исходники Кена Перлина мало объясняют даже при наличии комментариев.
Отступление
Поразительно, но судя по отзывам в личку и в комментарии оказалось, что далеко не все способны видеть вообще какую-либо разницу между простым сглаженным шумом в градациях серого и шумом Перлина. Но, наверное, из-за этого парадокса и появилась и поимела популярность та самая статья.
Попробую дать наводку:
первая картинка состоит из явно выраженных пикселей (увеличенных) разных оттенков серого:

Вторая же (шум Перлина) выглядит как черно-белые размытые черви.
Вот что получается после несложных операций в графическом редакторе (поиск границ, инвертирование, постеризация):
Перлин:

Картинка из статьи (применены точно те же операции):

Да, во фрактальном шуме, если октав много, то понять, что там лежит в оригинале — Перлин или нет уже и правда сложно. Но это ведь не повод назвать фрактальный шум Шумом Перлина.
На этом закончу с описанием разницы.
Конец отступления.
Рассмотрим двухмерный вариант. Пока напишем только класс-заготовку. Входящие данные — двухмерный вектор или два числа с плавающей точкой: x, y.
Возвращаемое значение — число от -1.0 до 1.0:
public class Perlin2d
{
public float Noise(float x, float y)
{
throw new NotImplementedException();
}
}
Пару слов об интерполяции
Идея обычного сглаженного шума в том, что есть дискретная сетка псевдослучайных значений, и для запрашиваемой точки происходит интерполяция между узлами сетки (чем ближе точка к какому-нибудь узлу сетки, тем больше его значение соответствует значению узла).
Здесь в третьем условном квадрате точка в самом центре после интерполяции будет иметь значение 3:

Рассмотрим детальнее как там получается тройка. Координаты точки:
x:2.5,
y:0.5
Целочисленные координаты точки (верхний левый угол квадрата):
x:2,
y:0
получаются округлением в меньшую сторону (функция floor).
Локальные координаты точки внутри квадрата получаются вычитанием:
x = 2.5 – 2 = 0.5,
y = 0.5 – 0 = 0.5
Берём значение левого верхнего угла квадрата (1) и верхнего правого (2). Интерполируем верхнюю грань используя локальную координату x (0.5). Линейная интерполяция выглядит так:
static float Lerp(float a, float b, float t)
{
// return a * (t - 1) + b * t; можно переписать с одним умножением (раскрыть скобки, взять в другие скобки):
return a + (b - a) * t;
}
Берём значение левого нижнего угла квадрата (2) и нижнего правого (7). Интерполируем нижнюю грань используя всё ту же локальную координату x (0.5).
Результаты:
верхняя: 1.5
нижняя: 4.5
Теперь осталась интерполяция верхней и нижней с использованием локальной координаты y (тоже 0.5):
1.5 * 0.5 + 4.5 * (1 – 0.5) = 3
Билинейная интерполяция самая простая но и результат не самый привлекательный.
Другие варианты интерполяции подразумевают модифицирование локальной координаты (параметра t) перед интерполяцией. Получаются более плавные переходы возле граничных значений (0 и 1).

В шуме Перлина задействован первый вариант, он даёт достаточно сильное искривление.
static float QunticCurve(float t)
{
return t * t * t * (t * (t * 6 - 15) + 10);
}
...
// комбинирование с функцией линейной интерполяции:
Lerp(a, b, QuinticCurve(t))
Главная идея и отличие шума Перлина
Всё очень просто:
1. В узлах сетки — псевдослучайные вектора (двухмерные для двухмерного шума, трехмерные для трехмерного и так далее), а не псевдослучайные числа.
2. Интерполируем между скалярными произведениями a) векторов от вершин квадрата до точки внутри квадрата (куба в трехмерном варианте) и b) псевдослучайных векторов (при описании шума Перлина их называют градиентными векторами).
В своём улучшенном варианте шума Кен Перлин использует всего 12 градиентных векторов. Для двухмерного варианта требуется всего 4 — по количеству граней (у квадрата их 4). Вектора направлены (условно из центра куба/квадрата) в сторону каждой из граней и не нормализованы.
Вот они:
{ 1, 0 }
{ -1, 0 }
{ 0, 1 }
{ 0,-1 }

Итак, каждому узлу сетки соответствует один из четырёх векторов. Пусть вектор у нас будет массивом float-ов.
float[] GetPseudoRandomGradientVector(int x, int y)
{
int v = // псевдо-случайное число от 0 до 3 которое всегда неизменно при данных x и y
switch (v)
{
case 0: return new float[]{ 1, 0 };
case 1: return new float[]{ -1, 0 };
case 2: return new float[]{ 0, 1 };
default: return new float[]{ 0,-1 };
}
}
Реализация
Нам понадобится скалярное произведение векторов:
static float Dot(float[] a, float[] b)
{
return a[0] * b[0] + a[1] * b[1];
}
Главный метод:
public float Noise(float fx, float fy)
{
// сразу находим координаты левой верхней вершины квадрата
int left = (int)System.Math.Floor(fx);
int top = (int)System.Math.Floor(fy);
// а теперь локальные координаты точки внутри квадрата
float pointInQuadX = fx - left;
float pointInQuadY = fy - top;
// извлекаем градиентные векторы для всех вершин квадрата:
float[] topLeftGradient = GetPseudoRandomGradientVector(left, top );
float[] topRightGradient = GetPseudoRandomGradientVector(left+1, top );
float[] bottomLeftGradient = GetPseudoRandomGradientVector(left, top+1);
float[] bottomRightGradient = GetPseudoRandomGradientVector(left+1, top+1);
// вектора от вершин кв��драта до точки внутри квадрата:
float[] distanceToTopLeft = new float[]{ pointInQuadX, pointInQuadY };
float[] distanceToTopRight = new float[]{ pointInQuadX-1, pointInQuadY };
float[] distanceToBottomLeft = new float[]{ pointInQuadX, pointInQuadY-1 };
float[] distanceToBottomRight = new float[]{ pointInQuadX-1, pointInQuadY-1 };
// считаем скалярные произведения между которыми будем интерполировать
/*
tx1--tx2
| |
bx1--bx2
*/
float tx1 = Dot(distanceToTopLeft, topLeftGradient);
float tx2 = Dot(distanceToTopRight, topRightGradient);
float bx1 = Dot(distanceToBottomLeft, bottomLeftGradient);
float bx2 = Dot(distanceToBottomRight, bottomRightGradient);
// готовим параметры интерполяции, чтобы она не была линейной:
pointInQuadX = QunticCurve(pointInQuadX);
pointInQuadY = QunticCurve(pointInQuadY);
// собственно, интерполяция:
float tx = Lerp(tx1, tx2, pointInQuadX);
float bx = Lerp(bx1, bx2, pointInQuadX);
float tb = Lerp(tx, bx, pointInQuadY);
// возвращаем результат:
return tb;
}
В качестве бонуса:
мультиоктавный шум
public float Noise(float fx, float fy, int octaves, float persistence = 0.5f)
{
float amplitude = 1; // сила применения шума к общей картине, будет уменьшаться с "мельчанием" шума
// как сильно уменьшаться - регулирует persistence
float max = 0; // необходимо для нормализации результата
float result = 0; // накопитель результата
while (octaves-- > 0)
{
max += amplitude;
result += Noise(fx, fy) * amplitude;
amplitude *= persistence;
fx *= 2; // удваиваем частоту шума (делаем его более мелким) с каждой октавой
fy *= 2;
}
return result/max;
}
И последнее — использование таблицы со случайными числами. В коде Кена Перлина такая таблица прописана вручную и достаются оттуда значения совсем по-другому. Здесь можно экспериментировать и от этого немало зависит равномерность шума и отсутствие в нём явных паттернов.
Я сделал
так
& 3 здесь обрезает любое int32 число до 3, читайте об операции AND на википедии
Операция типа % 3 тоже сработала бы, но намного медленней.
class Perlin2D
{
byte[] permutationTable;
public Perlin2D(int seed = 0)
{
var rand = new System.Random(seed);
permutationTable = new byte[1024];
rand.NextBytes(permutationTable); // заполняем случайными байтами
}
private float[] GetPseudoRandomGradientVector(int x, int y)
{
// хэш-функция с Простыми числами, обрезкой результата до размера массива со случайными байтами
int v = (int)(((x * 1836311903) ^ (y * 2971215073) + 4807526976) & 1023);
v = permutationTable[v]&3;
switch (v)
{
...
& 3 здесь обрезает любое int32 число до 3, читайте об операции AND на википедии
Операция типа % 3 тоже сработала бы, но намного медленней.
Исходный код целиком (без комментариев)
class Perlin2D
{
byte[] permutationTable;
public Perlin2D(int seed = 0)
{
var rand = new System.Random(seed);
permutationTable = new byte[1024];
rand.NextBytes(permutationTable);
}
private float[] GetPseudoRandomGradientVector(int x, int y)
{
int v = (int)(((x * 1836311903) ^ (y * 2971215073) + 4807526976) & 1023);
v = permutationTable[v]&3;
switch (v)
{
case 0: return new float[]{ 1, 0 };
case 1: return new float[]{ -1, 0 };
case 2: return new float[]{ 0, 1 };
default: return new float[]{ 0,-1 };
}
}
static float QunticCurve(float t)
{
return t * t * t * (t * (t * 6 - 15) + 10);
}
static float Lerp(float a, float b, float t)
{
return a + (b - a) * t;
}
static float Dot(float[] a, float[] b)
{
return a[0] * b[0] + a[1] * b[1];
}
public float Noise(float fx, float fy)
{
int left = (int)System.Math.Floor(fx);
int top = (int)System.Math.Floor(fy);
float pointInQuadX = fx - left;
float pointInQuadY = fy - top;
float[] topLeftGradient = GetPseudoRandomGradientVector(left, top );
float[] topRightGradient = GetPseudoRandomGradientVector(left+1, top );
float[] bottomLeftGradient = GetPseudoRandomGradientVector(left, top+1);
float[] bottomRightGradient = GetPseudoRandomGradientVector(left+1, top+1);
float[] distanceToTopLeft = new float[]{ pointInQuadX, pointInQuadY };
float[] distanceToTopRight = new float[]{ pointInQuadX-1, pointInQuadY };
float[] distanceToBottomLeft = new float[]{ pointInQuadX, pointInQuadY-1 };
float[] distanceToBottomRight = new float[]{ pointInQuadX-1, pointInQuadY-1 };
float tx1 = Dot(distanceToTopLeft, topLeftGradient);
float tx2 = Dot(distanceToTopRight, topRightGradient);
float bx1 = Dot(distanceToBottomLeft, bottomLeftGradient);
float bx2 = Dot(distanceToBottomRight, bottomRightGradient);
pointInQuadX = QunticCurve(pointInQuadX);
pointInQuadY = QunticCurve(pointInQuadY);
float tx = Lerp(tx1, tx2, pointInQuadX);
float bx = Lerp(bx1, bx2, pointInQuadX);
float tb = Lerp(tx, bx, pointInQuadY);
return tb;
}
public float Noise(float fx, float fy, int octaves, float persistence = 0.5f)
{
float amplitude = 1;
float max = 0;
float result = 0;
while (octaves-- > 0)
{
max += amplitude;
result += Noise(fx, fy) * amplitude;
amplitude *= persistence;
fx *= 2;
fy *= 2;
}
return result/max;
}
}
Результат:

