Из закона всемирного тяготения известно, что на поверхности тел шарообразной формы ускорение свободного падения постоянно по модулю и направлено к центру шара. Для тел неправильной формы это правило, очевидно, не выполняется. В этой статье я покажу способ расчёта и визуализации ускорения свободного падения для таких тел. Расчёт будем производить на JavaScript, визуализировать — на WebGL с использованием библиотеки three.js.
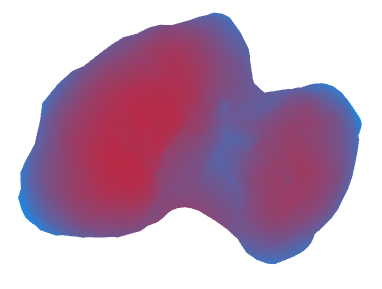
В итоге получим следующее (красным цветом отмечены области с большим ускорением свободного падения, синим — с малым):
Для расчетов гравитационного потенциала планет используется следующая формула:
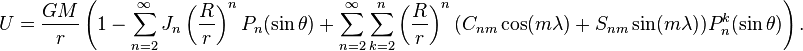
Но, к сожалению, при малых r этот ряд сходится медленно, а при очень малых r вообще расходится. Поэтому для расчета гравитационного потенциала на поверхности небесных тел эта формула не годится. В общем случае, придется провести интегрирование по всему объёму тела.
Трёхмерное тело можно представить в виде наборов треугольных граней, с заданными координатами вершин. Далее будем предполагать, что плотность тела постоянна (для кометы это примерно соответствует истине). Гравитационный потенциал в заданной точке будет равен сумме потенциалов всех тетраэдров, с основанием в этих гранях и с вершиной в заданной точке (мы ищем не гравитационный потенциал, а ускорение свободного падения, которое есть градиент потенциала, но рассуждения остаются теми же).
Для начала нам нужно найти ускорение, которое производит масса тетраэдра на точку, находящуюся в его вершине. Для этого нужно произвести интегрирование по всему объёму тетраэдра. К сожалению данный интеграл не берётся в элементарных функциях, поэтому придётся пойти на хитрость.

Сила, действующая на точку в вершине тетраэдра приблизительно в три раза больше, чем сила, вызванная гравитацией шара, помещенного в середину основания тетраэдра (масса шара при этом равна массе тетраэдра). Т. е. F1≈3*F2. Это равенство лучше выполняется при малом угле раствора тетраэдра. Для оценки величины отклонения равенства от строгого, я сгенерировал несколько тысяч рандомных тетраэдров и вычислил для них эту величину.
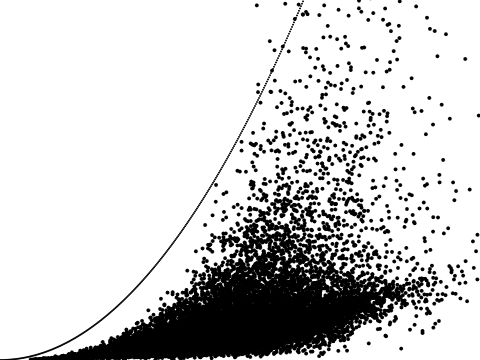
На графике по оси абсцисс показано отношение периметра треугольного основания к расстоянию от вершины до центра основания. По оси ординат — величина ошибки. Как видно, величину ошибки можно представить квадратичной функцией. За редким исключением все точки находятся ниже параболы (исключения нам погоду особо не испортят).
Величину гравитационного ускорения будем вычислять с заданной относительной погрешностью. Если ошибка вычисления превышает эту погрешность, то разбиваем наш тетраэдр на четыре части по основанию и вычисляем ускорение для этих частей по отдельности, затем суммируем.
Ускорение мы находим с точностью до некоторого постоянного, для данного тела, коэффициента, зависящего от массы (или плотности) тела, гравитационной постоянной и некоторых других параметров. Этот коэффициент мы учтём позже.
Вычисление ускорения от трёхмерного тела производим суммированием по всем тетраэдрам, образованным гранями тела и заданной точкой (о чём я писал ранее).
Вычисляем гравитационное и центробежное ускорения на комете (вращение кометы вызывает ускорение порядка 25% от гравитационного, поэтому пренебрегать им нельзя). Относительную погрешность я выставил в 0,01. Казалось бы это много, но по факту при вычислении погрешность получается раза в три меньше и при визуализации разница абсолютно не заметна (т. к. минимальная разница в цвете пикселей составляет 1/256≈0,004). А если выставить погрешность меньше, то время расчёта увеличивается.
При погрешности, равной 0,01, расчёт выполняется 1-2 секунды, поэтому оформляем его через setInterval, во избежание подвисания браузера.
Теперь стоит рассказать о формате работы с 3D телом. Тут всё просто. Это объект, состоящий из трёх массивов: вершины, нормали и треугольные грани.
Массив вершин хранит объекты-векторы координат вершин. Массив нормалей — векторы нормалей вершин. Массив граней — массивы из трёх чисел, хранящие номера вершин.
Модель кометы Чурюмова-Герасименко я скачал с сайта ESA и упростил её в 3Ds Max. В исходной модели было несколько десятков тысяч вершин и граней, но для нашей задачи это слишком много, т. к. вычислительная сложность алгоритма зависит от произведения количества вершин на количество граней. Модель сохранена в формате obj.
В библиотеке three.js есть функция OBJLoader для загрузки этого формата, но при загрузке остается только информация о вершинах, а информация о гранях теряется, что не подходит для нашей задачи. Поэтому я её несколько модифицировал.
Итак, объект из файла мы загрузили, затем вычислили вектор ускорения в каждой его вершине, теперь необходимо его визуализировать. Для этого нужно создать сцену, настроить камеру и свет, добавить и раскрасить нашу модель.
Сцена создаётся просто.
С камерой тоже никаких проблем.
Для создания камеры мы использовали функцию THREE.PerspectiveCamera(fov, aspect, near, far), где:
fov — высота поля зрения камеры в градусах;
aspect — отношение горизонтального угла зрения камеры к вертикальному;
near — расстояние до ближнего плана (то, что находится ближе, не будет рендериться);
far — расстояние до дальнего плана.
Ставим свет.
Создаём визуализатор.
Для работы с моделями в three.js удобно использовать класс BufferGeometry.
Задаём материал.
Загружаем координаты вершин.
Вычисляем цвет вершин.
Также нам понадобится отобразить направления ускорения свободного падения в каждой вершине.
С визуализацией закончили. Смотрим, что получилось.
Демо 1.
Как видим, ускорение свободного падения на комете от 40 до 80 тысяч раз меньше, чем на Земле. Максимальное отклонение вектора ускорения от нормали составляет порядка 60-70 градусов. Мелкие и крупные камни на этих участках вероятно не задерживаются и потихоньку скатываются в области, где угол не такой большой.
Можно поиграться с телами другой формы. Демо 2.
Видим, что для куба максимальное ускорение (в центре грани) составляет 1,002 ускорения для шара такой же массы, но на самом деле эта величина чуть меньше единицы (сыграло роль то, что мы считали с относительной погрешностью 0,01). Для куба, в отличие от тетраэдра, существуют точные формулы расчёта ускорений и точное значение для центра грани составляет (для куба со стороной, равной 1):

Для шара того же объёма:
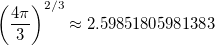
Их отношение составляет 0.999376 и лишь слегка не дотягивает до единицы.
В заключение вопрос. Существуют ли тела, у которых хотя бы в одной точке отношение абсолютной величины гравитационного ускорения к ускорению на поверхности шара той же массы и объёма больше единицы? Если да, то для какого тела это отношение максимально? Во сколько раз это отношение больше единицы, в разы или на доли процентов?
В итоге получим следующее (красным цветом отмечены области с большим ускорением свободного падения, синим — с малым):

Гифка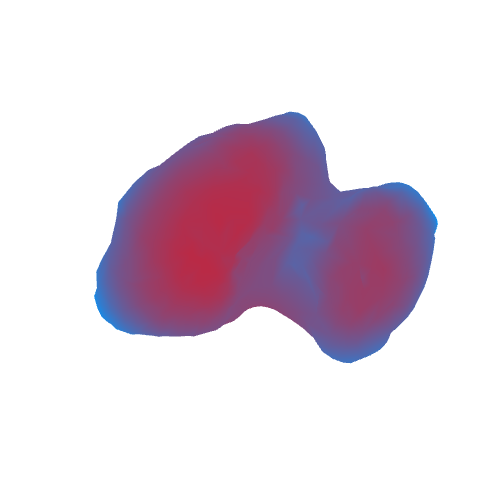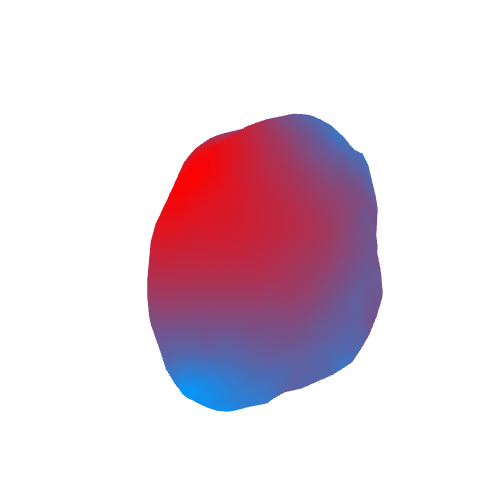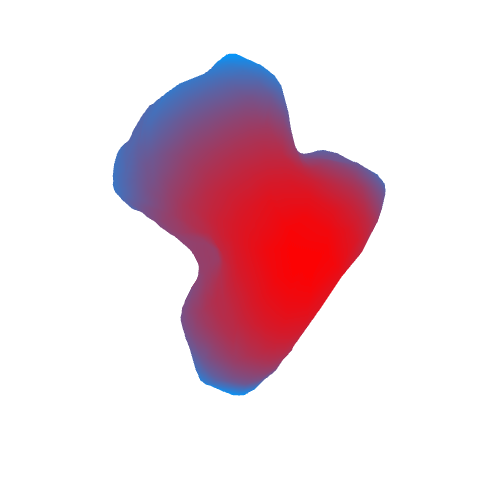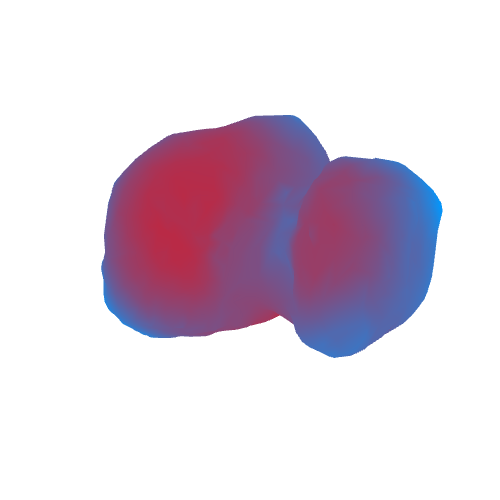
Ось вращения на гифке условная. Она не совпадает с осью вращения кометы.
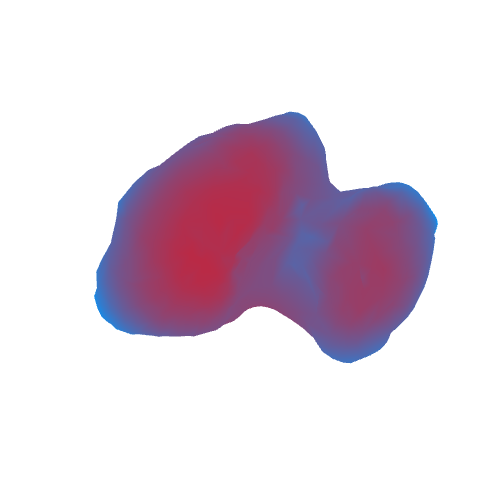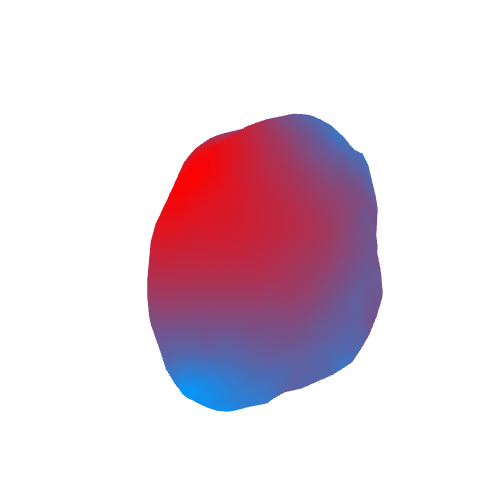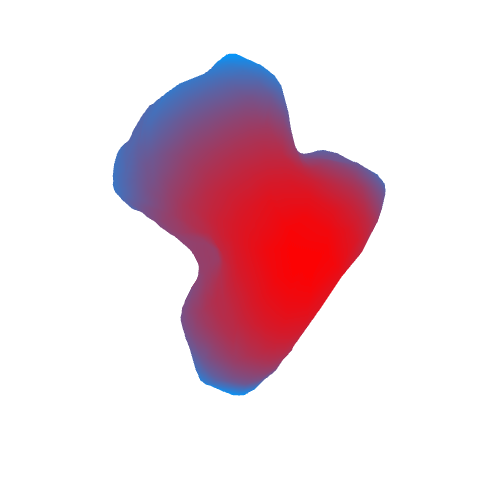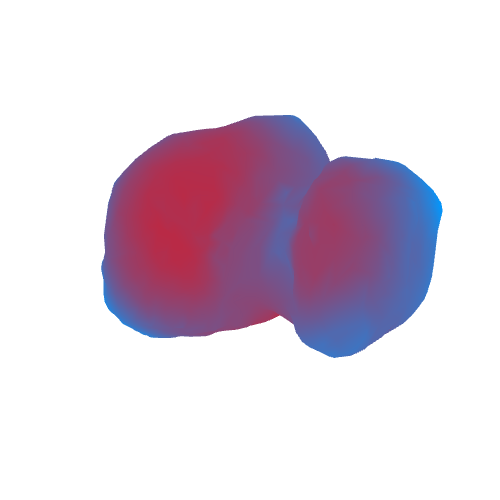
Ось вращения на гифке условная. Она не совпадает с осью вращения кометы.
Для расчетов гравитационного потенциала планет используется следующая формула:
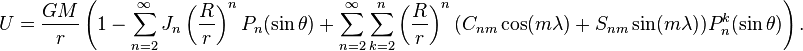
Но, к сожалению, при малых r этот ряд сходится медленно, а при очень малых r вообще расходится. Поэтому для расчета гравитационного потенциала на поверхности небесных тел эта формула не годится. В общем случае, придется провести интегрирование по всему объёму тела.
Трёхмерное тело можно представить в виде наборов треугольных граней, с заданными координатами вершин. Далее будем предполагать, что плотность тела постоянна (для кометы это примерно соответствует истине). Гравитационный потенциал в заданной точке будет равен сумме потенциалов всех тетраэдров, с основанием в этих гранях и с вершиной в заданной точке (мы ищем не гравитационный потенциал, а ускорение свободного падения, которое есть градиент потенциала, но рассуждения остаются теми же).
Для начала нам нужно найти ускорение, которое производит масса тетраэдра на точку, находящуюся в его вершине. Для этого нужно произвести интегрирование по всему объёму тетраэдра. К сожалению данный интеграл не берётся в элементарных функциях, поэтому придётся пойти на хитрость.

Сила, действующая на точку в вершине тетраэдра приблизительно в три раза больше, чем сила, вызванная гравитацией шара, помещенного в середину основания тетраэдра (масса шара при этом равна массе тетраэдра). Т. е. F1≈3*F2. Это равенство лучше выполняется при малом угле раствора тетраэдра. Для оценки величины отклонения равенства от строгого, я сгенерировал несколько тысяч рандомных тетраэдров и вычислил для них эту величину.

На графике по оси абсцисс показано отношение периметра треугольного основания к расстоянию от вершины до центра основания. По оси ординат — величина ошибки. Как видно, величину ошибки можно представить квадратичной функцией. За редким исключением все точки находятся ниже параболы (исключения нам погоду особо не испортят).
Величину гравитационного ускорения будем вычислять с заданной относительной погрешностью. Если ошибка вычисления превышает эту погрешность, то разбиваем наш тетраэдр на четыре части по основанию и вычисляем ускорение для этих частей по отдельности, затем суммируем.

Ускорение мы находим с точностью до некоторого постоянного, для данного тела, коэффициента, зависящего от массы (или плотности) тела, гравитационной постоянной и некоторых других параметров. Этот коэффициент мы учтём позже.
Пришло время кода
function force_pyramide(p1, p2, p3, rel) {
// начальная точка в (0, 0, 0)
// rel - относительная погрешность
var volume = (1/6) * triple_product(p1, p2, p3); // объём тетраэдра
if (volume == 0)
return new vector3(0, 0, 0);
if (!rel)
rel = 0.01;
var p0 = middleVector(p1, p2, p3); // вектор центра основания
var len = p0.length();
var per = perimeter(p1, p2, p3); // периметр основания
var tan_per = per / len;
var error = 0.015 * sqr(tan_per); // та самая эмпирическая квадратичная функция
if (error > rel) {
var p12 = middleVector(p1, p2);
var p13 = middleVector(p1, p3);
var p23 = middleVector(p2, p3);
return sumVector(
force_pyramide(p1, p12, p13, rel),
force_pyramide(p2, p23, p12, rel),
force_pyramide(p3, p13, p23, rel),
force_pyramide(p12, p23, p13, rel)
);
}
var ratio = 3 * volume * Math.pow(len, -3);
return new vector3(p0.x, p0.y, p0.z).multiplyScalar(ratio);
}
Вычисление ускорения от трёхмерного тела производим суммированием по всем тетраэдрам, образованным гранями тела и заданной точкой (о чём я писал ранее).
Скрытый текст
function force_object(p0, obj, rel) {
var result = new vector3(0, 0, 0);
for (var i = 0; i < obj.faces.length; i++) {
p1 = subVectors(obj.vertices[obj.faces[i][0] - 1], p0);
p2 = subVectors(obj.vertices[obj.faces[i][1] - 1], p0);
p3 = subVectors(obj.vertices[obj.faces[i][2] - 1], p0);
var f = force_pyramide(p1, p2, p3, rel);
result = addVectors(result, f);
}
return result;
}
Вычисляем гравитационное и центробежное ускорения на комете (вращение кометы вызывает ускорение порядка 25% от гравитационного, поэтому пренебрегать им нельзя). Относительную погрешность я выставил в 0,01. Казалось бы это много, но по факту при вычислении погрешность получается раза в три меньше и при визуализации разница абсолютно не заметна (т. к. минимальная разница в цвете пикселей составляет 1/256≈0,004). А если выставить погрешность меньше, то время расчёта увеличивается.
При погрешности, равной 0,01, расчёт выполняется 1-2 секунды, поэтому оформляем его через setInterval, во избежание подвисания браузера.
Код
var rel = 0.01;
// относительная погрешность
var scale = 1000;
// модель задана в километрах, переводим в метры
var grav_ratio = 6.672e-11 * 1.0e+13 / (sqr(scale) * volume);
// масса кометы 1е+13 кг
var omega2 = sqr(2 * Math.PI / (12.4 * 3600));
// период вращения кометы 12,4 часов
function computeGrav() {
info.innerHTML = 'Расчёт: ' + (100 * item / object3d.vertices.length).toFixed() + '%';
for (var i = 0; i < 50; i++) {
var p0 = object3d.vertices[item];
grav_force[item] = force_object(p0, object3d, rel).multiplyScalar(grav_ratio);
// гравитационное ускорение
circular_force[item] = new vector3(omega2 * p0.x * scale, omega2 * p0.y * scale, 0);
// центробежное ускорение, ось вращения совпадает с осью z
abs_grav_force[item] = grav_force[item].length();
abs_circular_force[item] = circular_force[item].length();
item++;
if (item >= object3d.vertices.length) {
console.timeEnd('gravity calculate');
clearInterval(timerId);
accelSelect();
init();
animate();
break;
}
}
}
var item = 0;
console.time('gravity calculate');
var timerId = setInterval(computeGrav, 1);
Теперь стоит рассказать о формате работы с 3D телом. Тут всё просто. Это объект, состоящий из трёх массивов: вершины, нормали и треугольные грани.
var obj = {
vertices: [],
normals: [],
faces: []
};
Массив вершин хранит объекты-векторы координат вершин. Массив нормалей — векторы нормалей вершин. Массив граней — массивы из трёх чисел, хранящие номера вершин.
Модель кометы Чурюмова-Герасименко я скачал с сайта ESA и упростил её в 3Ds Max. В исходной модели было несколько десятков тысяч вершин и граней, но для нашей задачи это слишком много, т. к. вычислительная сложность алгоритма зависит от произведения количества вершин на количество граней. Модель сохранена в формате obj.
В библиотеке three.js есть функция OBJLoader для загрузки этого формата, но при загрузке остается только информация о вершинах, а информация о гранях теряется, что не подходит для нашей задачи. Поэтому я её несколько модифицировал.
Код
function objLoad(url) {
var result;
var xhr = new XMLHttpRequest();
xhr.open('GET', url, false);
xhr.onreadystatechange = function(){
if (xhr.readyState != 4) return;
if (xhr.status != 200) {
result = xhr.status + ': ' + xhr.statusText + ': ' + xhr.responseText;
}
else {
result = xhr;
}
}
xhr.send(null);
return result;
}
function objParse(url) {
var txt = objLoad(url).responseText;
var lines = txt.split('\n');
var result;
// v float float float
var vertex_pattern = /v( +[\d|\.|\+|\-|e|E]+)( +[\d|\.|\+|\-|e|E]+)( +[\d|\.|\+|\-|e|E]+)/;
// f vertex vertex vertex ...
var face_pattern1 = /f( +-?\d+)( +-?\d+)( +-?\d+)( +-?\d+)?/;
// f vertex/uv vertex/uv vertex/uv ...
var face_pattern2 = /f( +(-?\d+)\/(-?\d+))( +(-?\d+)\/(-?\d+))( +(-?\d+)\/(-?\d+))( +(-?\d+)\/(-?\d+))?/;
// f vertex/uv/normal vertex/uv/normal vertex/uv/normal ...
var face_pattern3 = /f( +(-?\d+)\/(-?\d+)\/(-?\d+))( +(-?\d+)\/(-?\d+)\/(-?\d+))( +(-?\d+)\/(-?\d+)\/(-?\d+))( +(-?\d+)\/(-?\d+)\/(-?\d+))?/;
// f vertex//normal vertex//normal vertex//normal ...
var face_pattern4 = /f( +(-?\d+)\/\/(-?\d+))( +(-?\d+)\/\/(-?\d+))( +(-?\d+)\/\/(-?\d+))( +(-?\d+)\/\/(-?\d+))?/;
var obj = {
vertices: [],
normals: [],
faces: []
};
for (var i = 0; i < lines.length; i++) {
var line = lines[i].trim();
if ((result = vertex_pattern.exec(line)) !== null) {
obj.vertices.push(new vector3(
parseFloat(result[1]),
parseFloat(result[2]),
parseFloat(result[3])
));
}else if ((result = face_pattern1.exec(line)) !== null) {
obj.faces.push([
parseInt(result[1]),
parseInt(result[2]),
parseInt(result[3])
]);
if (result[4])
obj.faces.push([
parseInt(result[1]),
parseInt(result[3]),
parseInt(result[4])
]);
}else if ((result = face_pattern2.exec(line)) !== null) {
obj.faces.push([
parseInt(result[2]),
parseInt(result[5]),
parseInt(result[8])
]);
if (result[11])
obj.faces.push([
parseInt(result[2]),
parseInt(result[8]),
parseInt(result[11])
]);
}else if ((result = face_pattern3.exec(line)) !== null) {
obj.faces.push([
parseInt(result[2]),
parseInt(result[6]),
parseInt(result[10])
]);
if (result[14])
obj.faces.push([
parseInt(result[2]),
parseInt(result[10]),
parseInt(result[14])
]);
}else if ((result = face_pattern4.exec(line)) !== null) {
obj.faces.push([
parseInt(result[2]),
parseInt(result[5]),
parseInt(result[8])
]);
if (result[11])
obj.faces.push([
parseInt(result[2]),
parseInt(result[8]),
parseInt(result[11])
]);
}
}
obj.normals = computeNormalizeNormals(obj);
return obj;
}
Итак, объект из файла мы загрузили, затем вычислили вектор ускорения в каждой его вершине, теперь необходимо его визуализировать. Для этого нужно создать сцену, настроить камеру и свет, добавить и раскрасить нашу модель.
Сцена создаётся просто.
scene = new THREE.Scene();
С камерой тоже никаких проблем.
var fieldWidth = 500; // размеры холста в пикселях
var fieldHeight = 500;
camera = new THREE.PerspectiveCamera(50, fieldWidth / fieldHeight, 0.01, 10000);
scene.add(camera);
cameraZ = 3 * boundingSphereRadius;
// boundingSphereRadius - радиус сферы, описанной вокруг нашего тела
camera.position.x = 0;
camera.position.y = 0;
camera.position.z = cameraZ;
camera.lookAt(new THREE.Vector3(0, 0, 0)); // камера смотрит в начало координат
Для создания камеры мы использовали функцию THREE.PerspectiveCamera(fov, aspect, near, far), где:
fov — высота поля зрения камеры в градусах;
aspect — отношение горизонтального угла зрения камеры к вертикальному;
near — расстояние до ближнего плана (то, что находится ближе, не будет рендериться);
far — расстояние до дальнего плана.
Ставим свет.
var ambientLight = new THREE.AmbientLight(0xffffff);
scene.add(ambientLight);
Создаём визуализатор.
renderer = new THREE.WebGLRenderer({antialias: true});
renderer.setClearColor(0xffffff); // цвет фона
renderer.setPixelRatio(window.devicePixelRatio);
renderer.setSize(fieldWidth, fieldHeight); // задаём размер холста
container.appendChild(renderer.domElement); // привязываемся к холсту
Всё вместе
var container;
var camera, scene, renderer;
var axis;
var mesh;
var boundingSphereRadius, cameraZ;
var lines = [];
var angleGeneral = 0;
function init() {
container = document.getElementById('container');
scene = new THREE.Scene();
var fieldWidth = 500;
var fieldHeight = 500;
camera = new THREE.PerspectiveCamera(50, fieldWidth / fieldHeight, 0.01, 10000);
scene.add(camera);
var ambientLight = new THREE.AmbientLight(0xffffff);
scene.add(ambientLight);
loadModel();
cameraZ = 3 * boundingSphereRadius;
camera.position.x = 0;
camera.position.y = 0;
camera.position.z = cameraZ;
camera.lookAt(new THREE.Vector3(0, 0, 0));
axis = new THREE.Vector3(0.6, 0.8, 0); //
renderer = new THREE.WebGLRenderer({antialias: true});
renderer.setClearColor(0xffffff);
renderer.setPixelRatio(window.devicePixelRatio);
renderer.setSize(fieldWidth, fieldHeight);
container.appendChild(renderer.domElement);
}
Для работы с моделями в three.js удобно использовать класс BufferGeometry.
var geometry = new THREE.BufferGeometry();
Задаём материал.
var material = new THREE.MeshLambertMaterial( {
side: THREE.FrontSide, // отображаться будет только передняя сторона грани
vertexColors: THREE.VertexColors // грани окрашиваются градиентом по цветам их вершин
});
Загружаем координаты вершин.
var vertices = new Float32Array(9 * object3d.faces.length);
for (var i = 0; i < object3d.faces.length; i++) {
for (var j = 0; j < 3; j++) {
vertices[9*i + 3*j ] = object3d.vertices[object3d.faces[i][j] - 1].x;
vertices[9*i + 3*j + 1] = object3d.vertices[object3d.faces[i][j] - 1].y;
vertices[9*i + 3*j + 2] = object3d.vertices[object3d.faces[i][j] - 1].z;
}
}
geometry.addAttribute('position', new THREE.BufferAttribute(vertices, 3));
Вычисляем цвет вершин.
var colors = addColor();
geometry.addAttribute('color', new THREE.BufferAttribute(colors, 3));
function addColor() {
var colorMin = [0.0, 0.6, 1.0]; // цвет точек с минимальным ускорением
var colorMax = [1.0, 0.0, 0.0]; // то же с максимальным
var colors = new Float32Array(9 * object3d.faces.length);
for (var i = 0; i < object3d.faces.length; i++) {
for (var j = 0; j < 3; j++) {
var intensity = (abs_force[object3d.faces[i][j] - 1] - forceMin) / (forceMax - forceMin);
colors[9*i + 3*j ] = colorMin[0] + (colorMax[0] - colorMin[0]) * intensity;
colors[9*i + 3*j + 1] = colorMin[1] + (colorMax[1] - colorMin[1]) * intensity;
colors[9*i + 3*j + 2] = colorMin[2] + (colorMax[2] - colorMin[2]) * intensity;
}
}
return colors;
}
Также нам понадобится отобразить направления ускорения свободного падения в каждой вершине.
Код
var lines;
function addLines() {
lines = new Array();
for (var i = 0; i < object3d.vertices.length; i++) {
var color;
var ratio;
if (angle_force[i] < 90) {
color = 0x000000; // Вектор ускорения направлен в сторону тела
ratio = -0.2 * boundingSphereRadius / forceMax;
}
else {
color = 0xdddddd; // Вектор ускорения направлен наружу
ratio = 0.2 * boundingSphereRadius / forceMax;
}
var material = new THREE.LineBasicMaterial({
color: color
});
var geometry = new THREE.Geometry();
var point1 = object3d.vertices[i];
var point2 = new THREE.Vector3();
point2.copy(force[i]);
point2.addVectors(point1, point2.multiplyScalar(ratio));
geometry.vertices.push(
new THREE.Vector3(point1.x, point1.y, point1.z),
new THREE.Vector3(point2.x, point2.y, point2.z)
);
var line = new THREE.Line(geometry, material);
rotateAroundWorldAxis(line, axis, angleGeneral);
if (hair.checked)
scene.add(line);
lines.push(line);
}
}
С визуализацией закончили. Смотрим, что получилось.
Демо 1.
Как видим, ускорение свободного падения на комете от 40 до 80 тысяч раз меньше, чем на Земле. Максимальное отклонение вектора ускорения от нормали составляет порядка 60-70 градусов. Мелкие и крупные камни на этих участках вероятно не задерживаются и потихоньку скатываются в области, где угол не такой большой.
Можно поиграться с телами другой формы. Демо 2.
Видим, что для куба максимальное ускорение (в центре грани) составляет 1,002 ускорения для шара такой же массы, но на самом деле эта величина чуть меньше единицы (сыграло роль то, что мы считали с относительной погрешностью 0,01). Для куба, в отличие от тетраэдра, существуют точные формулы расчёта ускорений и точное значение для центра грани составляет (для куба со стороной, равной 1):

Для шара того же объёма:
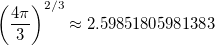
Их отношение составляет 0.999376 и лишь слегка не дотягивает до единицы.
В заключение вопрос. Существуют ли тела, у которых хотя бы в одной точке отношение абсолютной величины гравитационного ускорения к ускорению на поверхности шара той же массы и объёма больше единицы? Если да, то для какого тела это отношение максимально? Во сколько раз это отношение больше единицы, в разы или на доли процентов?
