Теорема о четырёх красках — это математическая формулировка, связанная с картами. Все примеры карт, которые я нашёл в Интернете, были слишком сложными для введения, поэтому я набросал собственный неказистый рисунок:
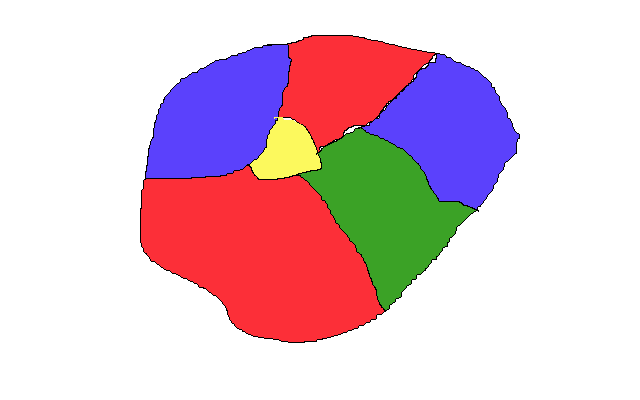
Если посмотреть под другим углом, то можно воспринимать её как граф — достаточно ужать все области до кругов и соединить круги, соответствующие соседним областям карты:

Теорема о четырёх цветах утверждает, что для разметки любого рисунка, похожего на мой, (или соответствующего ему графа) достаточно четырёх цветов, чтобы никакие соседние области не имели одинаковой раскраски. Это значит, что если мы возьмём карту США или Европы, даже со всеми этими причудливыми границами, и присвоим каждому штату или стране свой цвет, то для разметки всей карты будет достаточно четырёх цветов.
Некоторым картам не нужны все четыре цвета, им достаточно всего двух или трёх. Карта, которую можно раскрасить одним цветом, будет не очень интересной, так что её мы пропустим.
Первое, что поразило меня, как разработчика ПО: четыре цвета — это совсем мало. Кажется поразительным, что любой граф можно раскрасить всего четырьмя цветами; мне кажется, что если я нарисую графы некоторых из кодовых баз, с которыми я работал, где рёбрами будут соединены обменивающиеся данными объекты, то им запросто может потребоваться дюжина цветов.
Итак, как вы догадались, в теореме о четырёх цветах есть одно условие. Граф обязан быть планарным (плоским). Это значит, что никакие рёбра не могут пересекаться. Он обязательно должен иметь возможность накладываться на двухмерную плоскость без пересечений. То есть если мы имеем граф с пересечениями, который нельзя наложить на плоскость, то теорема о четырёх цветах к нему не применима. Для него потребуется больше четырёх цветов, но для его отрисовки без пересечений потребуется не менее трёх измерений.
Поэтому можно сделать так:

но не так:
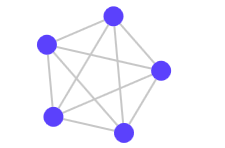
Так что интересного в этих цветах? Почему они должны кого-то волновать? Зачем вообще я пишут этот пост? Кратко это можно выразить одним словом — сложность. Количество цветов, необходимых для раскраски графа, обозначает его сложность — для более сложных графов потребуется большее количество цветов. Чтобы понять, как это будет выглядеть на практике, давайте попробуем пораскрашивать графы. Представленные ниже графы имеют одинаковое количество узлов, но для их раскраски требуется разное количество цветов (в оригинале статьи графы интерактивны и их можно раскрашивать, нажимая на узлы):
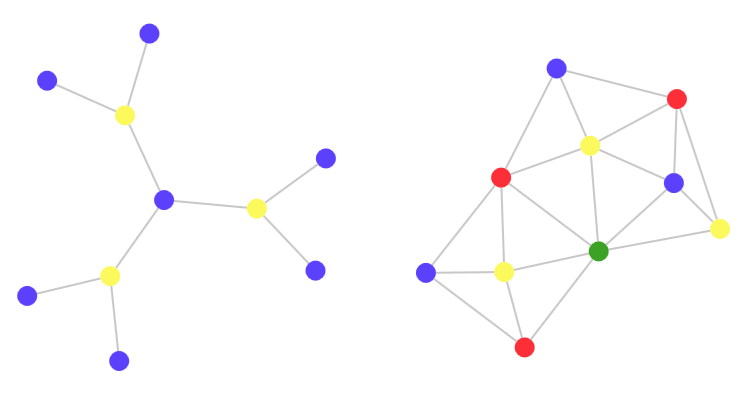
Второй граф интуитивно кажется более сложным, или, по крайней мере, менее упорядоченным. Существует конкретный измеряемый способ оценки его сложности: для его раскраски требуется больше цветов. Для второго графа требуется четыре цвета, для первого — всего два. Почему?
Сложность возникает из самой природы соединений графа. Некоторые компоненты второго графа сильно взаимосвязаны, в отличие от узлов первого. На самом деле, первый граф создан на основе набора правил: это дерево. Второй граф создан мной: я произвольно щёлкал мышью, создавая множество взаимосвязей.
Граф может содержать любое количество связей без увеличения количества цветов, пока он упорядочен в соответствии с определёнными логическими правилами. Количество узлов, соединённых с каждым узлом, при этом не важно:
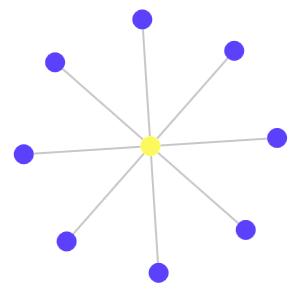
как и количество элементов в графе:
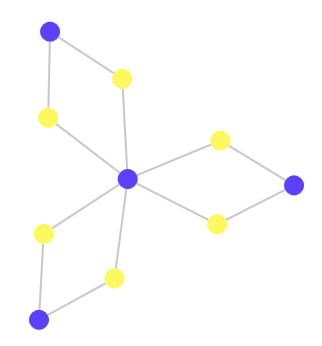
На самом деле увеличивают количество цветов в графе компоненты с большим количеством связей. В треугольнике мы получаем три цвета, но треугольник на самом деле очень сильно взаимосвязан для того количества узлов, которые в нём имеются: это полный граф. Интересной задачей является переход от трёх к четырём цветам. При этом нужно добавить соединения между компонентами, которые уже соединены. Допустим, мы хотим объединить два следующих графа:

Существуют способы сделать это без увеличения общей сложности и с увеличением. Всё зависит от того, как добавляются новые рёбра:

(Второй граф отрисовывается с пересечённым ребром, но на самом деле является планарным. Если потянуть в оригинале статьи нижние узлы вверх, то он исправится.)
В первом графе я использовал узел 3 для соединения со вторым графом; узел 3 является как-бы «интерфейсом» ромба, ограничивая доступ к нему. Благодаря следованию этому паттерну сложность графа не увеличивается.
Во втором графе узлы 1, 2 и 4 имеют соединения с более крупным подграфом. В этом случае нет одного узла, ограничивающего доступ к ромбу; более крупный граф имеет возможность соединяться с несколькими узлами в ромбе. Это привело к увеличению сложности всей системы. Кроме того, сложность каскадно распространилась на бо́льшую часть системы — я не могу изменить только один из цветов узла, а должен распространить изменения на бо́льший подграф.
Эти графы похожи на граф зависимостей в кодовой базе. Если добавить узел для каждого класса и отрисовать рёбра между классами, которые обмениваются данными, то в результате у нас получится граф, похожий на один из представленных выше. На упоминанием мной терминов «компоненты» и «модули» повлияло то, что я воспринимал эти графы с точки зрения ПО. В последнем примере мы затрагиваем важную тему — можно управлять растущей кодовой базой, не увеличивая её сложность, если управлять тем, как модули соединяются друг с другом. Кодовая база, состоящая из небольших взаимосвязанных модулей, обменивающихся данными чётко заданным способом, будет иметь меньшую сложность по сравнению с базой, в которой модули обмениваются данными беспорядочно.
Это пример того, что лучше управлять взаимодействиями вдоль точки, а не вдоль ребра. Я имею в виду, что модули, имеющие одну точку взаимодействия, будут способны поддерживать собственную динамику, не загрязняя сложность кодовой базы. Если программисты не думают о том, как они соединяют модули в кодовой базе, а получившиеся модули имеют множество точек взаимодействия, то сложность кодовой базы будет расти.
С точки зрения цветового измерения сложности деревья очень просты. Для их раскраски требуется всего два цвета. Структура дерева оберегает от создания взаимосвязанных кластеров, приводящих к скачкам сложности, потому что родительские узлы ограничивают доступ к дочерним узлам. В схеме зависимости родительские узлы похожи на абстракцию поверх функционала, обеспечиваемого дочерними узлами. Если бы другие узлы соединялись с дочерними узлами напрямую, то абстракция была бы разрушена.
Однако большинство схем зависимостей не являются деревьями из-за многократного использования кода. Программисту нужно, чтобы один объект мог использоваться множеством других объектов. Но только до определённой точки — нам не нужно, чтобы web-представление общалось напрямую с уровнем хранения данных: во-первых, web-слой находится на отдельном уровне абстракции, во-вторых, у web-слоя скорее всего будут другие обязанности, поэтому при общении непосредственно с уровнем хранения данных в одном месте будет происходить слишком многое.
Основным выводом из этих размышлений для меня стало то, что хорошим способом управления сложностью кодовой базы является использование объектов, создающих API поверх группы других. Сложность графа никогда не увеличивается, если мы создаём соединения, подключаясь к точке, ограничивающей внутренний граф. Но если открыть наружу «внутренности», то можно быстро прийти к очень сложным графам.

Если посмотреть под другим углом, то можно воспринимать её как граф — достаточно ужать все области до кругов и соединить круги, соответствующие соседним областям карты:

Теорема о четырёх цветах утверждает, что для разметки любого рисунка, похожего на мой, (или соответствующего ему графа) достаточно четырёх цветов, чтобы никакие соседние области не имели одинаковой раскраски. Это значит, что если мы возьмём карту США или Европы, даже со всеми этими причудливыми границами, и присвоим каждому штату или стране свой цвет, то для разметки всей карты будет достаточно четырёх цветов.
Некоторым картам не нужны все четыре цвета, им достаточно всего двух или трёх. Карта, которую можно раскрасить одним цветом, будет не очень интересной, так что её мы пропустим.
Первое, что поразило меня, как разработчика ПО: четыре цвета — это совсем мало. Кажется поразительным, что любой граф можно раскрасить всего четырьмя цветами; мне кажется, что если я нарисую графы некоторых из кодовых баз, с которыми я работал, где рёбрами будут соединены обменивающиеся данными объекты, то им запросто может потребоваться дюжина цветов.
Итак, как вы догадались, в теореме о четырёх цветах есть одно условие. Граф обязан быть планарным (плоским). Это значит, что никакие рёбра не могут пересекаться. Он обязательно должен иметь возможность накладываться на двухмерную плоскость без пересечений. То есть если мы имеем граф с пересечениями, который нельзя наложить на плоскость, то теорема о четырёх цветах к нему не применима. Для него потребуется больше четырёх цветов, но для его отрисовки без пересечений потребуется не менее трёх измерений.
Поэтому можно сделать так:

но не так:

Сложность
Так что интересного в этих цветах? Почему они должны кого-то волновать? Зачем вообще я пишут этот пост? Кратко это можно выразить одним словом — сложность. Количество цветов, необходимых для раскраски графа, обозначает его сложность — для более сложных графов потребуется большее количество цветов. Чтобы понять, как это будет выглядеть на практике, давайте попробуем пораскрашивать графы. Представленные ниже графы имеют одинаковое количество узлов, но для их раскраски требуется разное количество цветов (в оригинале статьи графы интерактивны и их можно раскрашивать, нажимая на узлы):

Второй граф интуитивно кажется более сложным, или, по крайней мере, менее упорядоченным. Существует конкретный измеряемый способ оценки его сложности: для его раскраски требуется больше цветов. Для второго графа требуется четыре цвета, для первого — всего два. Почему?
Сложность возникает из самой природы соединений графа. Некоторые компоненты второго графа сильно взаимосвязаны, в отличие от узлов первого. На самом деле, первый граф создан на основе набора правил: это дерево. Второй граф создан мной: я произвольно щёлкал мышью, создавая множество взаимосвязей.
Граф может содержать любое количество связей без увеличения количества цветов, пока он упорядочен в соответствии с определёнными логическими правилами. Количество узлов, соединённых с каждым узлом, при этом не важно:

как и количество элементов в графе:

На самом деле увеличивают количество цветов в графе компоненты с большим количеством связей. В треугольнике мы получаем три цвета, но треугольник на самом деле очень сильно взаимосвязан для того количества узлов, которые в нём имеются: это полный граф. Интересной задачей является переход от трёх к четырём цветам. При этом нужно добавить соединения между компонентами, которые уже соединены. Допустим, мы хотим объединить два следующих графа:

Существуют способы сделать это без увеличения общей сложности и с увеличением. Всё зависит от того, как добавляются новые рёбра:

(Второй граф отрисовывается с пересечённым ребром, но на самом деле является планарным. Если потянуть в оригинале статьи нижние узлы вверх, то он исправится.)
В первом графе я использовал узел 3 для соединения со вторым графом; узел 3 является как-бы «интерфейсом» ромба, ограничивая доступ к нему. Благодаря следованию этому паттерну сложность графа не увеличивается.
Во втором графе узлы 1, 2 и 4 имеют соединения с более крупным подграфом. В этом случае нет одного узла, ограничивающего доступ к ромбу; более крупный граф имеет возможность соединяться с несколькими узлами в ромбе. Это привело к увеличению сложности всей системы. Кроме того, сложность каскадно распространилась на бо́льшую часть системы — я не могу изменить только один из цветов узла, а должен распространить изменения на бо́льший подграф.
Разработка ПО
Эти графы похожи на граф зависимостей в кодовой базе. Если добавить узел для каждого класса и отрисовать рёбра между классами, которые обмениваются данными, то в результате у нас получится граф, похожий на один из представленных выше. На упоминанием мной терминов «компоненты» и «модули» повлияло то, что я воспринимал эти графы с точки зрения ПО. В последнем примере мы затрагиваем важную тему — можно управлять растущей кодовой базой, не увеличивая её сложность, если управлять тем, как модули соединяются друг с другом. Кодовая база, состоящая из небольших взаимосвязанных модулей, обменивающихся данными чётко заданным способом, будет иметь меньшую сложность по сравнению с базой, в которой модули обмениваются данными беспорядочно.
Это пример того, что лучше управлять взаимодействиями вдоль точки, а не вдоль ребра. Я имею в виду, что модули, имеющие одну точку взаимодействия, будут способны поддерживать собственную динамику, не загрязняя сложность кодовой базы. Если программисты не думают о том, как они соединяют модули в кодовой базе, а получившиеся модули имеют множество точек взаимодействия, то сложность кодовой базы будет расти.
С точки зрения цветового измерения сложности деревья очень просты. Для их раскраски требуется всего два цвета. Структура дерева оберегает от создания взаимосвязанных кластеров, приводящих к скачкам сложности, потому что родительские узлы ограничивают доступ к дочерним узлам. В схеме зависимости родительские узлы похожи на абстракцию поверх функционала, обеспечиваемого дочерними узлами. Если бы другие узлы соединялись с дочерними узлами напрямую, то абстракция была бы разрушена.
Однако большинство схем зависимостей не являются деревьями из-за многократного использования кода. Программисту нужно, чтобы один объект мог использоваться множеством других объектов. Но только до определённой точки — нам не нужно, чтобы web-представление общалось напрямую с уровнем хранения данных: во-первых, web-слой находится на отдельном уровне абстракции, во-вторых, у web-слоя скорее всего будут другие обязанности, поэтому при общении непосредственно с уровнем хранения данных в одном месте будет происходить слишком многое.
Основным выводом из этих размышлений для меня стало то, что хорошим способом управления сложностью кодовой базы является использование объектов, создающих API поверх группы других. Сложность графа никогда не увеличивается, если мы создаём соединения, подключаясь к точке, ограничивающей внутренний граф. Но если открыть наружу «внутренности», то можно быстро прийти к очень сложным графам.